桁架结构几何非线性优化设计在石油井架设计中的运用

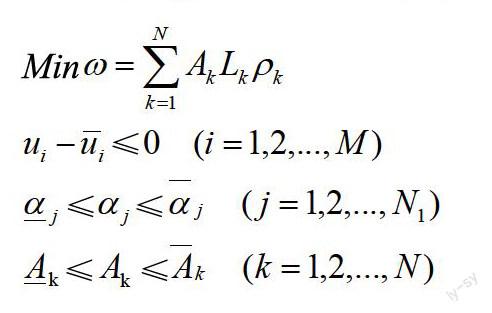
摘要：在现实生活中，类似石油井架的一些桁架结构形式较多，而在进行该类结构的设计时，还需使用几何非线性优化设计方法，才能获得更为精确的设计结果。文章在对桁架结构几何非线性优化设计问题展开分析的基础上，在石油井架设计中进行了该种设计方法的运用。

关键词：桁架结构；几何非线性优化设计；石油井架设计；有限元静力分析 文献标识码：A

中图分类号：TE922 文章编号：1009-2374（2016）17-0009-02 DOI：10.13535/j.cnki.11-4406/n.201617.004

作为石油钻采机械的重要组成部分，石油井架的设计得到了石油行业的重视。但就目前来看，使用线性稳定分析和有限元静力分析方法进行井架的设计，将无法满足所有井架的应用需求。因此，还需要在石油井架设计中进行桁架结构几何非线性优化设计方法的运用，从而更好地满足石油工业的发展需要。

1 几何非线性分析的概念

在工程设计过程中，通常使用的理论都是线弹性理论，比如几何方程、平衡方程和物理方程等。但是一些实际工程并不能保持上述线性关系，所以就无法使用线弹性方程进行工程力学关系的描述。例如，工程结构形状的不连续变化、在外载荷作用下出现的工程结构局部材料进入塑性、钢架结构大变形和高温下的结构蠕变，都属于需要利用非线性理论描述的问题。而在工程结构的非线性分析中，又可以划分成几何非线性、材料非线性和状态非线性。所谓的几何非线性，其实就是其应变位移是非线性的。比如，工程结构出现的大位移、大转动和小应变问题，就属于几何非线性问题。

与线性方法不同，几何非线性方法使用的小变形线性理论平衡方程需要在工程结构未发生变形的情况下建立。但是在实际生活中，平衡方程需要在变形之后建立。所以结构变形状态将与平衡状态出现差异，这种差异则会对结构设计产生一定的影响。使用几何大变形结构分析理论，则能够使二者保持统一协调。此外，采用线性分析方法，一定能够获得问题的解。但是，使用几何非线性分析方法，在杆件界面过小或荷载过大的情况下，就可能无法求到解。而这也说明，工程结构可能不存在变形与平衡统一的状态。

2 桁架结构的几何非线性优化设计方法

2.1 桁架结构的几何非线性稳定性分析

针对小变形桁架结构，可以使用几何非线性欧拉理论进行结构稳定性的分析。而使用该理论，其实就是以欧拉稳定条件为临界点理论的约束条件，可以顺利求得方程的正确解。在任何桁架结构中，该方法都能够适用。而针对高荷载和大截面的桁架结构，也可以通过将其自动归结为临界点理论进行问题的求解。具体来讲，就是在桁架变形状态下进行平衡方程的建立，然后利用几何非线性理论进行结构稳定性的分析。但此时，结构变形是未知的，所以还需要使用迭代的方法进行求解，并且直到前后两次迭代的解的误差小于给定误差。在进行迭代求解时，需要使用线性平衡方程进行内力向量的求解，然后利用欧拉稳定条件进行杆件的横截面积的修改。针对细长圆杆，需要进行材料对应的长细比下界的设置，而针对中长杆和短杆，需要有相应的稳定条件，以便对横截面积的修改进行约束。完成该两个步骤之后，需要使用胡克定律进行各杆变形量的求解。但是，如果遭遇超静定问题，则需要进行与自由度数相同个数的杆件变形量的计算。此时就不需要进行其与杆件变形量的计算，但是需要得到杆件的内力值。根据计算得到的杆件变形量，可以对各节点位移进行计算，然后进行节点位移向量的求解。在这一过程中，需要先进行各杆的变形量，然后再计算长度。针对已经变形的几何构形，需要建立内力平衡方程，然后进行平衡方程的求解，从而得到待定的内力。最后根据求得的结果，就可以判断桁架结构是否稳定。

2.2 桁架结构的几何非线性优化设计

2.2.1 优化模型。完成桁架结构的几何非线性稳定分析后，就可以使用工程结构优化设计方法进行工程结构的优化。利用该方法可以将优化算法与结构分析结合起来，从而得到满足设计要求的最优设计方案。针对确定几何形状和给定拓扑安排的桁架结构，想要进行结构的优化设计就可以重量极小为目标。而结构优化设计模型如下式，需要进行A的范围的求解：

式中：A为杆件的横截面积，即设计变量向量；则为某个方向的位移界限；为给定应力上下限；为尺寸上下限；N、M、N1、Lk和ρk分别为设计变量总数、位移约束总数、杆件总数、第K类杆件长度和第K类杆件的重度。

在处理该模型时，需要使用准则法，并且按照应力法进行应力约束的处理，以便形成相应的函数。在此基础上，通过适当变换就可以得到迭代公式，然后通过求解获得桁架结构的线性优化设计结果。而由于整个过程未进行本构关系的引入，所以也可以利用该模型求解桁架结构的非线性优化设计问题。

2.2.2 桁架的静力分析。针对空间桁架结构，可以使用Newton-Raphson法进行结构的静力分析。在分析的过程中，可以采取单元刚度阵进行杆件的局部坐标系的表示，从而使结构坐标得到适当的整理，继而满足优化公式推导需要。在此基础上，还要将公式转换成全局坐标系，从而对结构的整体稳定情况进行掌握。考虑到大部分桁架结构整体失稳时会出现位移发散现象，而一些结构则会出现位移过大或位移振荡不收敛的问题，所以在利用模型求解后，一旦位移收敛于有限的确定值，就可以认为结构整体比较稳定。

2.2.3 桁架的敏度分析。就目前来看，在使用几何非线性分析法进行桁架结构的优化设计时，通常需要使用位移对设计变量的导数。所以在结构优化设计的过程中，还需要进行位移灵敏度的求解。针对线性问题则可以利用一些推导能用显式进行位移对设计变量的导数的表达，但是针对几何非线性问题，考虑到位移与载荷之间的非线性关系，则需要使用其他方法进行结构的敏度分析。具体来讲，就是需要将位移灵敏度显式进行两边求导。在求导的过程中，需要对设计变量求偏导，从而得到关于位移灵敏度的线性方程组。而在该方程组中，结构刚度矩阵是在几何非线性的影响下得到的，所以还可以根据总刚的组装规则进行公式的简化。最后通过求解位移灵敏度的系数矩阵，就能够得到单元刚度阵有所改变的杆件设计优化结果。

2.2.4 桁架的近似重分析。在进行桁架结构的优化设计时，往往需要进行设计变量的多次修改，从而得到最优的设计方案。而在每次进行方案的修改后，都需要进行结构的重分析。但是非线性问题的重分析则需要较大的计算量，所以将导致设计矛盾的出现。因此为了利用几何非线性优化设计方法进行大型实际结构的优化设计，还需要使用近似重分析法对修改后的设计方案进行分析。使用该方法，其实就是直接将一次迭代的计算结果作为二次迭代的输入值，并且直至两次迭代相差不大。但在解决线性问题时，由于需要进行刚度阵的重新组装，所以使用该方法并没有实际意义。在几何非线性问题的解决上，使用该方法可以将几十次迭代过程简化成一两次迭代，所以能够有效降低非线性分析的工作量。

3 桁架结构的几何非线性优化设计在石油井架设计中的运用

在生产的过程中，石油井架时常会出现破坏现象，从而给石油企业的生产带来阻碍。所以在设计石油井架的过程中，还应该实现井架结构的优化设计，从而使井架得到更好的应用。而考虑到井架结构形式多样，并且承受的载荷并不相同的问题，还需要使用几何非线性桁架结构优化设计方法对井架设计进行优化。

3.1 平面桁架的优化设计

通过将上述方法编写成计算机程序，就可以利用几何非线性优化设计方法进行平面桁架的优化设计。而石油井架的平面桁架结构具有39根杆件，各杆件许用应力为1.5×108N/m2，截面积下限和上限分别为1cm2和1000cm2，各杆截面积的初始设计值为50cm2。使用几何非线性方法进行该结构的优化设计，可以将设计纵向边缘节点的y向位移不超过±7cm，并且横向边缘节点的水平位移不超过±1cm，从而对结构变形进行约束。而通过优化设计，则能够发现得到的目标函数和杆件截面积与线性优化设计结果有较大的差异。

3.2 A型井架的优化设计

针对A型井架结构，其大腿横截面为边长1.5m的等边三角形，结构内共有188个杆件，自由度174个，横截面初始设计值为40.21cm2，并且以横杆、斜杆和弦管为设计变量。同时各设计变量下限为5.88cm2，应力约束为1.6×108N/m2，并且需要承受自重、钩载和风载。在使用几何非线性方法进行该结构的优化设计时，可以将顶部y向位移不超过±12cm，然后通过载荷简化将每个节点沿z向的作用力设定为-3×103N，从而实现对该结构的优化设计。

4 结语

总而言之，相较于线性计算方法，非线性计算方法将更加精确。在进行一些高柔结构的优化设计时，使用几何非线性设计方法将得到差别较大的计算结果。而在现实生活中，包括石油井架在内的很多桁架结构都属于高柔结构，所以还需要使用几何非线性方法进行结构的优化设计，从而提升结构的稳定性。因此，通过本文对桁架结构的几何非线性优化设计问题展开分析，可以为相关工作的开展提供指导。

参考文献

[1] 俞然刚，庄向仕，周金顺，等.桁架式跨河管架的优化设计及地震可靠性评价[J].地震工程学报，2013，（2）.

[2] 胡桂川，刘敬花.基于CAE分析的机械结构优化设计[J].机械设计与研究，2011，（3）.

[3] 赵宏安，王敏，辛力，等.陕西延长石油科研中心结构方案优化及设计难点分析[J].施工技术，2015，（10）.

[4] 周明峰，孟文俊.基于APDL的圆管带式输送机桁架梁优化设计[J].起重运输机械，2013，（11）.

[5] 陈少杰，段敬民，赵洪波.桁架结构优化设计的改进蚁群算法[J].工业建筑，2010，（1）.

作者简介：刘斌（1979-），男，四川长宁人，四川宏华石油设备有限公司机械工程师，研究方向：石油钻井机械设计。

（责任编辑：黄银芳）