基于渗透系数序贯高斯模拟的水库渗漏量不确定性分析

张 飞,温忠辉,戴凤君,李　伟

(1.河海大学水文水资源学院,江苏 南京　210098;2.江苏水文水资源勘测局镇江分局,江苏 镇江　212003;3. 江苏省地质调查研究院,江苏 南京　210018)

基于渗透系数序贯高斯模拟的水库渗漏量不确定性分析

张 飞1,温忠辉1,戴凤君2,李伟3

(1.河海大学水文水资源学院,江苏 南京210098;2.江苏水文水资源勘测局镇江分局,江苏 镇江212003;3. 江苏省地质调查研究院,江苏 南京210018)

摘要：水库库底地层渗透系数是影响水库渗漏量的主要因素之一,研究渗透系数的空间变异特征可为水库渗漏量计算结果的可靠性分析提供科学依据。以天津市北塘水库库底地层渗透系数为研究对象,先利用克里金插值对该参数系列进行了插补,再对插补后的渗透系数系列进行了500次序贯高斯模拟,最后分析了其空间变异性对库区渗漏量计算值不确定性的影响。结果表明:库底地层垂向渗透系数空间结构可用球状模型描述,在变程1 210 m范围内具有高度空间相关性。以2005年7月16日渗漏量计算值总体为例,最小值与最大值分别为1 389.49 m3/d、1 897.30 m3/d,且落在区间1 600～1 850 m3/d的频率高达77.6%。

关键词：渗透系数;条件模拟;空间变异性;水库渗漏量;不确定性

地表水和地下水的相互作用是自然界中普遍存在的一种现象。正确认识地表水与地下水之间的相互作用,尤其是水量和水质的时空变化规律研究及交换水量的准确计算,对水资源的综合管理及合理开发利用具有重要的科学意义[1]。进入21世纪,国内外许多组织和机构都将两者的相互作用作为水文学及水文地质学方面研究的热点问题[2]。

水文地质参数的空间变异性是影响地表水与地下水相互作用强度的主要因素之一。其中,渗透系数在野外实际条件下的空间变异性较其他水文地质参数要大得多,最大值与最小值相差可达13个数量级[3]。这就决定了渗透系数必须作为随机变量处理。同时渗透系数又具有一定程度上的结构性,比如,含水介质是在特定地质条件下沉积形成的,具有一定成层性[4]。因此,地表水与地下水之间交换量计算的可靠度在很大程度上依赖于参数随机场的模拟是否反映出实际地区参数的空间变异性。

胡伏生等[5]利用条件模拟对内蒙古霍林河市主要含水层渗透系数的分布特征进行了分析;陈彦等[4]采用Monte Carlo法来研究含水介质渗透系数空间变异性对地下水数值模拟的影响;彭伟等[6]进行了渗透系数的序贯高斯模拟对污染物运移的不确定性研究;束龙仓等[7]在对北塘水库库底地层渗透系数进行Monte Carlo模拟的基础上,进行了地表水与地下水交换量的不确定性研究。综合前人研究的成果,与Monte Carlo法相比,条件模拟既考虑了参数的随机性,又考虑了参数的结构性,更能客观地反映参数实际变化特征[6]。笔者在文献[7]研究的基础上,运用地质统计学的原理和方法,分析参数的随机性和空间相关性,进一步探讨参数条件模拟对交换量不确定性的影响。

1序贯高斯模拟法

对于某一特定的含水层而言,其空间上每一点的渗透系数都是确定的。但由于渗透系数难于准确获取,并且获取所有点的渗透系数也不太现实,因此如何合理利用有限个参数样本来推断含水层参数在空间上的分布特征成为难点之一。条件模拟是地质统计学一个重要的随机模拟手段,它是以区域化变量为基础、借助变异函数来研究既具有随机性又具有结构性的自然现象的手段。20世纪90年代我国在水土资源领域开始引入条件模拟进行应用研究,并受到广泛关注[8]。在条件模拟的多种方法中,序贯高斯模拟法由于灵活、简单、高效,成为条件模拟最常用的方法之一。

顾名思义,序贯高斯模拟就是将顺序模拟和高斯模拟相结合的一种随机模拟方法。序贯高斯模拟的适用前提是模拟变量必须符合正态分布,若不符合,则须先将其进行正态变换。该方法前人已作了大量的叙述,限于篇幅,这里不再赘述。序贯高斯模拟方法原理及算法的实现可参见文献[6]。

2地表水与地下水交换量计算方法

天津市北塘水库库区垂向渗漏过程中,渗漏水量受下伏相对隔水层的阻挡,库水先垂向渗漏补给库底含水层,之后在侧向水力梯度作用下以侧向渗流为主。因此,在渗漏量计算过程中,可以将上述过程概化为侧向渗流。

库区渗漏量按照式(1)～(3)进行计算:

(1)

(2)

(3)

式中:Q为地下水与地表水交换量;Qi为各个分区的交换量;n为分区个数;Ki为各分区水量交换层渗透系数;Ai为各分区的面积;Ji为地下水与地表水之间的水力梯度,无量纲;Li为各分区的形心到对应地下水水位观测井的距离;ΔHi为库水位与地下水的水位差。

利用序贯高斯模拟法生成渗透系数随机场,渗流方向的确定仍沿用文献[7]提出的D8算法。主要计算步骤如下:

a. 将库底地层在平面上剖分成多个大小相同的正方形网格,逐一计算每个网格中心点到周围所有观测井的水力梯度,取其最大值作为该点渗流方向,得到任一网格的Ji;

b. 将序贯高斯模拟法生成的参数模拟值分别赋值到相应的网格上,得到任一网格所代表的Ki;

c. 根据式(2)计算得到任一网格Ai上地表水与地下水交换量Qi;

d. 将所有网格各自的Qi相加即得水库渗漏总量Q;

e. 重复步骤a～c,得到水库渗漏量Q的多次模拟值。

3实例研究

3.1研究区概况

北塘水库位于天津市塘沽区北塘镇西北约2 km,是一座已建成的中型平原水库。地理坐标为117°38′E～117°41′E,39°06′N～39°08′N。2003年12月北塘水库增容扩建后,总库容达到3 977万m3,设计水位7.00 m,蓄水面积7.31 km2,围堤总长约10.40 km。库底地层岩性以黏土、粉质黏土为主,夹粉砂、粉土透镜体,整体上含水不丰富,埋藏较浅,地下径流微弱。库区地下水为孔隙潜水和微承压水,分别分布于上部陆相层和第一海相层上部的粉砂、粉土层中。库区周边地下水埋深0.55～2.56 m,平均1.42 m,北侧和东北侧地下水水位较高。北塘水库地理位置、平面形状及库底地层岩芯采样点位置见图1。

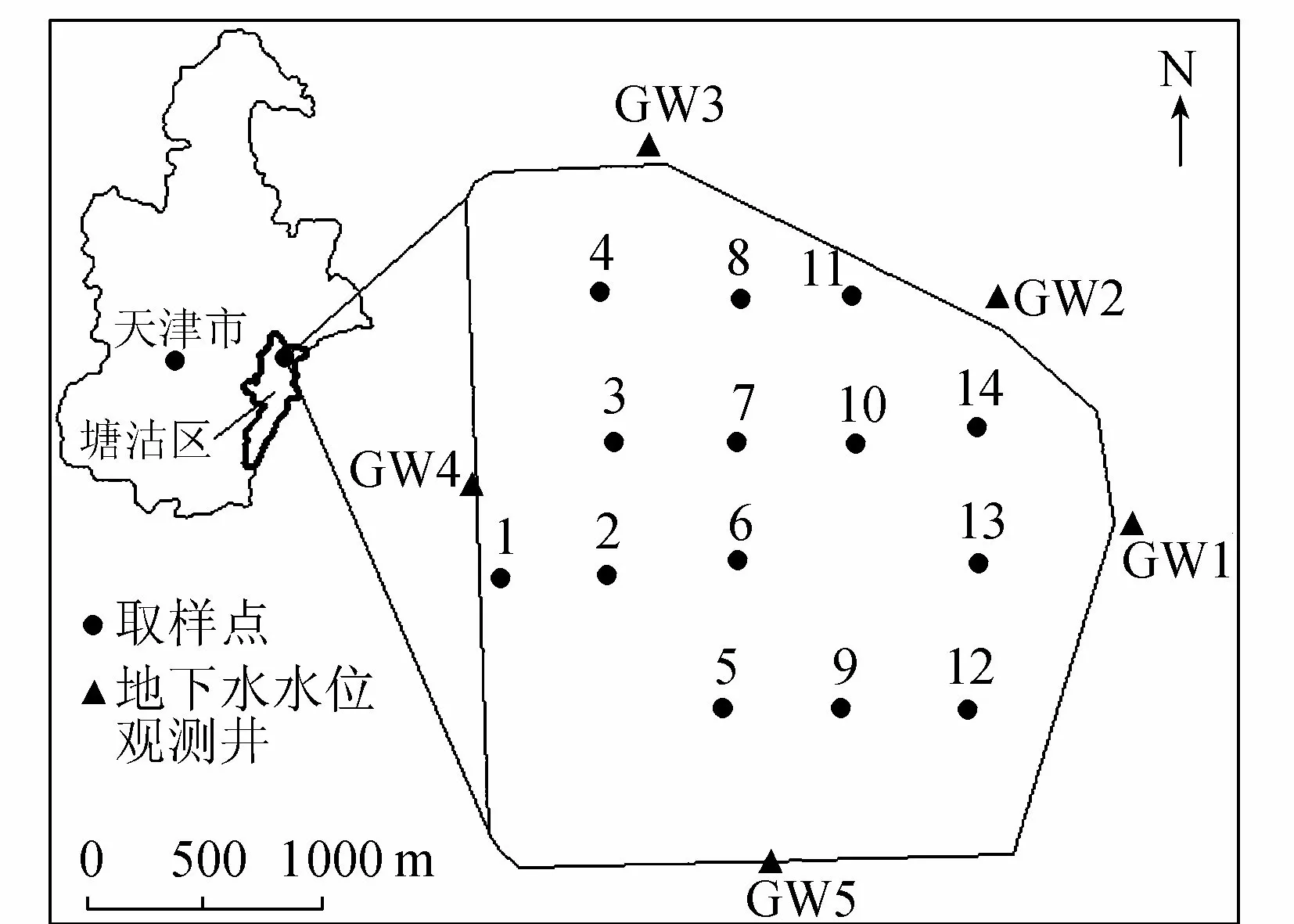
图1　北塘水库地理位置、平面形状及库底地层岩芯采样点位置

库区共布置了岩芯采样点14个,在对土样进行室内颗粒分析试验后,选取ALYAMANI&SEN公式最终计算得到这14个测点的渗透系数。

本文选取2005年7月16日,8月31日,9月15日地表水与地下水水位动态观测资料进行分析计算,地表水、地下水水位动态资料见表1。

表1　地表水、地下水水位动态观测资料　m

3.2序贯高斯模拟

渗透系数半方差函数分析及序贯高斯模拟均用GS+9.0软件进行计算和模拟,研究区参数模拟的空间分布图用ArcMap10.2软件绘制,参数统计和P-P图在SPSS12.0软件中进行。

3.2.1渗透系数统计特征分析

为了对研究区渗透系数分布有个总体的认识,对这14个测点样本进行了统计分析及非参数检验[9],结果表明:样本分布类型为对数正态,均值为4.56 cm/d,标准差为8.67,最大值为24.71 cm/d,最小值为8.35×10-5cm/d,变异系数为190%，属高强度变异[10]。插值精度在很大程度上受到数据变异性的影响,在相同的插值精度条件下,数据变异性越大所需的样本数越多。若仅对这14个测点样本进行地质统计分析,则资料不够充分,并且库岸处布设点数较少。为了解决此问题,可以利用这14个样本进行克里金插值,得到如图2所示的库区库底地层渗透系数等值线,然后在该图中较均匀地取点,并结合库底地层地质勘探资料,最终获得20个点来插补资料系列[11]。根据国外相关研究成果[12],虽然该方法获取的数据有一定近似性,但对数据的半定量及定性分析不会产生明显影响。

图2　库区库底地层渗透系数等值线(单位：cm/d)

对插补后的34个参数样本分别绘制正态(图3(a))和对数正态(图3(b))P-P概率图,相对于正态分布而言,该渗透系数系列更接近对数正态分布。将该系列取自然对数后,再对该参数系列进行K-S检验[13]。检验结果表明,在0.05显著性水平下,lnK系列的P>0.05,接受正态分布的原假设,故lnK系列服从正态分布,满足了序贯高斯模拟需以数据场呈正态分布的前提[14]。

图3　K系列的正态及对数正态P-P概率图

3.2.2半方差函数的结构分析

半方差函数是研究含水层渗透系数空间变异的一种有效方法。利用GS+9.0软件可以很方便地获得库底地层渗透系数的最佳理论半方差函数(图4)。

图4　含水层渗透系数半方差函数

图4中半方差函数为球状模型,C0=2.12,C0+C=39.52,a=1 210 m,R2=0.879,RSS=29.53。其中:C0表示块金效应;C0+C表示基台值;C0/(C0+C)表示参数空间变异性程度,研究区渗透系数C0/(C0+C)值为0.05%,属高度空间相关性[10]。a表示参数变程,即在该值范围内,观测值之间存在一定的相关性,观测值之间的距离超过该值时则相互独立。研究区参数变程为1 210 m,大于采样距离。综合以上分析,研究区渗透系数在变程1 210 m范围内具有高度的空间相关性。

3.2.3渗透系数条件模拟

利用图4半方差函数理论模型对库底地层渗透系数进行了500次序贯高斯模拟。为避免模拟过程中模拟值出现负值[15],在GS+9.0软件中将模拟值的上限和下限分别设为参数实测值的最大值和最小值。设定剖分网格大小为20 m×20 m,即每个网格面积为400 m2。将模拟的参数随机场导入ArcMap中转换成点位图,剔除研究区外的数据。最终得到插值数据18 048个,用于渗漏量的计算。图5列出模拟中随机抽取的两次条件模拟的参数空间分布图。

图5　渗透系数条件模拟实现

由图5可知,渗透系数具有明显的空间变异性,渗透系数较大的区域位于库区中北部,也是水库渗漏风险最大的区域,其他区域渗透系数较小。这是由于库区中北部第四系全新统上部陆相层在水库增容扩建期间破坏较为严重,下伏的粉砂和粉土层出露库底,而其他区域地层多为黏土类沉积物,透水性差[16]。

3.3渗流方向的确定

依据文献[7]提出的D8算法,分别计算每个网格中心点到周边5口观测井的水力梯度,取其最大值作为渗流方向,最终得到每个网格的Ji。图6为不同时刻渗流方向示意图。

图6　不同时刻渗流方向示意图

3.4计算渗漏量

在给每一网格Ji、Ki赋值的基础上,根据式(1)～(3)分别计算3个时刻的渗漏量,这就得到每个时刻一次渗透量模拟值。按照一共模拟500次渗透系数随机场计算,可得到每个时刻样本容量为500的渗漏量总体。渗漏量计算结果见表2，其频率分布见图7。

表2　水库渗漏量计算结果　m3/d

综合表2及图7分析,基于渗透系数序贯高斯模拟的渗漏量计算结果,最大值与最小值相差约1.4倍,频率分布呈偏右型。以7月16日计算的渗漏量总体为例,最小值与最大值分别为1 389.49 m3/d、1 897.30 m3/d,且落在区间1 600～1 850 m3/d的频率较高,其频率高达77.6%。

图7　2005年渗漏量频率分布

4结论

a. 库区渗透系数较大的区域位于中北部,也是水库渗漏风险最大的区域,其他区域渗透系数较小。与Monte Carlo法相比,基于序贯高斯模拟的渗透系数随机场既考虑了参数空间随机性,又考虑了参数的结构性,其模拟结果更能反映出实际库底地层地质条件。

b. 影响渗漏量的主要因素是渗透系数的空间变异性,同一时刻基于不同渗透系数随机计算出的渗漏量相差约1.4倍。此外,不同时刻空间渗流方向的变化也会对渗漏量的计算产生影响。

c. 针对其他的水文地质参数,如孔隙度、给水度、导水系数等,在对其进行正态检验或正态变换后,均可以通过多次序贯高斯模拟,产生大量不同插值结果的参数随机场,进而进行不确定性分析。若参数样本偏少,利用克里金插值来插补资料不失为一种有效的方法。

参考文献：

[1] 胡立堂,王忠静,赵建世,等.地表水和地下水相互作用及集成模型研究[J].水利学报,2007,38(1):54-59.(HU Litang,WANG Zhongjing,ZHAO Jianshi,et al.Advances in the interactions and integrated model between surface water and groundwater [J].Journal of Hydraulic Engineering,2007,38(1):54-59.(in Chinese))

[2] 胡俊锋,王金生,滕彦国.地下水与河水相互作用的研究进展[J].水文地质工程地质,2004 (1):108-113.(HU Junfeng,WANG Jinsheng,TENG Yanguo.Study progress of interaction between stream and groundwater [J].Hydrogeology and Engineering Geology,2004 (1):108-113.(in Chinese))

[3] FREEZE R A,CHERRY J A.Groundwater [M].Upper Saddle River,NJ:Prentice-Hall,1979.

[4] 陈彦,吴吉春.含水层渗透系数空间变异性对地下水数值模拟的影响[J].水科学进展,2005,16(4):482-487.(CHEN Yan,WU Jichun.Effect of the spatial variability of hydraulic conductivity in aquifer on the numerical simulation of groundwater [J].Advances in Water Science,2005,16(4):482-487.(in Chinese))

[5] 胡伏生,陈连竹,万力,等.含水层参数不确定性与地下水开采量可靠性评价[J].南京大学学报(自然科学版),1999,35(6):675-682.(HU Fusheng,CHEN Lianzhu,WAN Li,et al.Uncertainty of aquifer property and assessment of groundwater yield reliability [J].Journal of Nanjing University (Natural Sciences),1999,35(6):675-682.(in Chinese))

[6] 彭伟,吴剑锋,阎婷婷.渗透系数的条件模拟对污染物运移的不确定性分析[J].南京大学学报(自然科学版),2008,44(3):280-288.(PENG Wei,WU Jianfeng,YAN Tingting.Uncertainty analysis of the contaminant transport fate using conditional simulation of hydraulic conductivity [J].Journal of Nanjing University (Natural Sciences),2008,44(3):280-288.(in Chinese))

[7] 束龙仓,鲁程鹏,李伟.考虑参数不确定性的地表水与地下水交换量的计算方法[J].水文地质工程地质,2008 (5):68-71.(SHU longcang,LU Chengpeng,LI Wei.Calculation method of the exchange volume between surface water and groundwater based on uncertainty of parameters [J].Hydrogeology and Engineering Geology,2008 (5):68-71.(in Chinese))

[8] 陈亚新,徐英,史海滨,等.条件模拟原理和技术进展及在水资源系统中的应用[J].水科学进展,2002,13(2):246-252.(CHEN Yaxin,XU Ying,SHI Haibin,et al.Theory,development and application of the conditional simulation in water resources system [J].Advances in Water Science,2002,13(2):246-252.(in Chinese))

[9] 陈元芳.统计试验方法及应用[M].哈尔滨:黑龙江人民出版社,2000:25-65.

[10] 杨奇勇,杨劲松,姚荣江,等.耕地土壤有机质空间变异性的随机模拟[J].农业工程学报,2010,26(12):324-329.(YANG Qiyong,YANG Jinsong,YAO Rongjiang,et al.Stochastic simulation of cultivated soil organic matter spatial variability [J].Transactions of the Chinese Society of Agricultural Engineering,2010,26(12):324-329.(in Chinese))

[11] 郭建清,母敏霞,郑丽萍,等.浅层含水层水文地质参数的统计分析与空间相关性[J].勘察科学技术,2002(4):9-12.(GUO Jianqing,MU Minxia,ZHENG Liping,et al.Analysis on statistic distribution and spatial correlativity of hydrogeological parameters of shallow aquifer [J].Site Investigation Science and Technology,2002(4):9-12.(in Chinese))

[12] ROBERT J H,PETER K K.An application of geostatistical approach to the inverse problem in two-dimensional groundwater modeling [J].Water Resource Research,1984,20(7):1003-1020.

[13] 束龙仓,李伟.北塘水库库底地层渗透系数的随机特性分析[J].吉林大学学报(地球科学版),2007,37(2):216-220.(SHU Longcang,LI Wei.Analysis on the stochastic characteristic of the hydrauic conductivity of bottom stratum,Beitang Reservoir,Tianjin City [J].Journal of Jilin University(Earth Science Edition),2007,37(2):216-220.(in Chinese))

[14] 李保国,胡克林,陈德立,等.农田土壤表层饱和导水率的条件模拟[J].水利学报,2002(2):36-46.(LI Baoguo,HU Kelin,CHEN Deli,et al.Conditional simulation of soil surface saturated hydraulic conductivity at field scale [J].Journal of Hydraulic Engineering,2002(2):36-46.(in Chinese))

[15] 张泽谱,王学军.土壤微量元素含量空间分布的条件模拟[J].土壤学报,1998,35(3):424-429.(ZHANG Zepu,WANG Xuejun.Conditional simulation for spatial distribution of trace elements in soils [J].Acta Pedologica Sinica,1998,35(3):424-429.(in Chinese))

[16] 李伟.北塘水库对地下水的渗漏补给特性研究[D].南京:河海大学,2007.

Uncertainty analysis of reservoir leakage based on sequential Gaussian simulation of hydraulic conductivity

ZHANG Fei1,WEN Zhonghui1,DAI Fengjun2,LI Wei3

(1.CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China;2.ZhenjiangBranchofJiangsuProvinceHydrologyandWaterResourcesInvestigationBureau,Zhenjiang212003,China;3.GeologicalSurveyofJiangsuProvince,Nanjing210018,China)

Abstract：Hydraulic conductivity of the reservoir bottom stratum is one of the main factors affecting reservoir leakage. Studying the spatial variability of hydraulic conductivity can provide a scientific basis for the reliability analysis of the calculation results of reservoir leakage. Using the bottom stratum of the Beitang Reservoir as a case study, the parameter series were extended through Kriging interpolation. Then, the interpolated hydraulic conductivity was estimated by sequential Gaussian simulation which was carried out 500 times. Finally, the effect of the spatial variability of hydraulic conductivity on the uncertainty of calculated leakage was analyzed. The results show that the spatial structure of vertical hydraulic conductivity can be described by a spherical model, and it has a high spatial correlation within 1 210 m. As for the leakage calculated on July 16, 2005, the smallest value was 1 389.49 m3/d, the largest value was 1 897.30 m3/d, and the frequency of the calculated value falling into the range of 1 600 to 1 850 m3/d reached 77.6%.

Key words：hydraulic conductivity; conditional simulation; spatial variability; reservoir leakage; uncertainty

DOI：10.3880/j.issn.1004-6933.2016.03.013

基金项目:国家自然科学基金(41172203,41201029,41301017);中国水利水电科学研究院流域水循环模拟与调控国家重点实验室开放研究基金(IWHR-SKL-201502)

作者简介:张飞(1991—),男,硕士研究生,研究方向为地下水数值模拟及开发利用。E-mail:jeff91214@sina.com 通信作者:温忠辉,副教授。E-mail:wenzh2812@sina.com.cn

中图分类号：P641.2

文献标志码：A

文章编号：1004-6933(2016)03-0069-05

(收稿日期：2015-06-02编辑：徐娟)