DUCA双环多天线MIMO系统性能分析与研究

邵根富，姚颖莉，周杰,，菊池久和

（1.杭州电子科技大学自动化学院，浙江 杭州 310018；2.南京信息工程大学电子与信息工程学院，江苏 南京 210044；3.国立新泻大学工学部电气电子工学科，日本 新泻 950-2181）

DUCA双环多天线MIMO系统性能分析与研究

邵根富1，姚颖莉2，周杰2,3，菊池久和3

（1.杭州电子科技大学自动化学院，浙江 杭州 310018；2.南京信息工程大学电子与信息工程学院，江苏 南京 210044；3.国立新泻大学工学部电气电子工学科，日本 新泻 950-2181）

针对非频率选择性瑞利衰落信道，在三维（3D，three-dimensional）空间域信道模型中分析和研究紧凑型双环阵列（DUCA，double uniform circular array）多天线MIMO系统。采用互耦效应的等效电路模型，首次导出DUCA天线阵元间的信号衰落相关性的通用表达式，阐明互耦效应的影响机理。分析结果与传统MIMO线性阵列（ULA，uniform linear array）和单环阵列（UCA，uniform circular array）相比较，阵元空间配置及其互耦效应将对信号衰落相关性起到决定性作用。研究结果对未来massive MIMO多天线的设计和性能优化具有很好的指导意义。

MIMO多天线；双环阵列；互耦效应；信号衰落相关性

1 引言

随着宽带移动互联网接入技术的快速发展，对无线通信系统的优化和天线收发技术的研究变得至关重要。多输入多输出（MIMO，multiple input multiple output）多天线系统已经成为第4代（4G,4th generation）移动通信的关键技术之一，且已为5G LET-2025愿景规划提出了massive MIMO技术。MIMO具有提高频谱利用率以及系统信道容量的巨大优势[1～5]。MIMO的信道特性对于信号传输存在巨大的影响，因此，对基站(BS,base station)和移动台(MS,mobile station)之间的传输信道进行有效建模及对MIMO多天线阵列的研究也就显得非常必要，至今也还存在许多亟需解决的问题，其中包括：1) 大规模天线的数量和空间阵列的制约；2) 多天线MIMO系统的接收机复杂度高，对射频(RF,radio frequency)链、信号处理单元和多路信号的隔离算法都会带来更多额外消耗；3) 需要建立更精准合适的信道模型。因此，研究中不但要建立静态信道模型，还需要建立与通信场景相对应的动态信道模型[5～9]。随着目前移动终端小型化的发展，设计紧凑型多天线MIMO系统已成必然趋势。因此，阵元间互耦（MC，mutual coupling）效应已不可避免地成为影响MIMO多天线阵列设计与优化的重要因素[10～16]。文献[12～16]从理论上对MC效应进行分析，其仿真实验证明当阵元间距缩小到一定值时，MC效应可使接收信号衰落相关性变小，能够提高MIMO系统的信道容量。文献[13]仅讨论了天线阵元在平行和错位放置时，MC效应对信号衰落相关性的影响。文献[14～16]从理论和仿真上证明了如果能妥善处理MC效应，其影响还可以转变为有利因素。

在无线通信中通常需要天线系统在水平面内具有无方向性接收能力。传统的MIMO线性阵对波达信号的增益和方向性会因角度不同而改变。圆环阵（UCA）是由均匀分布在同心圆内的阵元构成。由于UCA阵结构对称，在水平面内具有全向辐射特征，而且具有互耦效应及占用空间相对较小等优点，在移动通信领域中具有广泛应用潜力。对比其他多种阵列结构，文献[17]论证了UCA阵列具有较好的接收性能。为简化理论推导难度，研究都针对二维空间域的MIMO多径统计衰落信道建模[17,18]与分析。但由实际测量得知俯仰方位同样对系统和信号衰落有显著的影响。结果显示在波达信号入射仰角（EOA,elevation of arrival）大于10°情况下，占有信号总能量的65%[20]。当EOA位于[0°,40°]，占有信号总能量的90%。因此，三维空间域的MIMO信道建模对于分析系统具有重要的实际意义，能构建更加理想合理的系统。本文针对非频率选择性瑞利衰落信道，在三维空间域信道模型中分析和研究紧凑型双环阵列多天线MIMO系统。分析中采用MC效应的等效电路网络模型，首次导出DUCA天线阵元间的信号衰落相关性的通用表达式，阐明了MC效应的影响机理。分析结果与传统的ULA和UCA阵列比较，得出阵列配置设计和互耦效应会对信号衰落相关性起到决定性作用，且系统性能主要取决于波达信号的方位，而波达信号扩展角参数对系统影响较小。分析结果对未来新型多天线MIMO阵列设计和系统优化具有很好的参考意义。

2 DUCA MIMO信道模型及互耦理论

在无线通信系统中BS和MS均可使用多天线MIMO阵列。通常提高多天线系统性能的主要方法之一是使任意两阵元间有充分的空间，以便能接收更多非相关的多径衰落信号。在无MC效应的条件下，研究者[20～26]对ULA、UCA和URA矩形阵列等进行过详细的分析和研究。随着目前终端小型化的发展趋势，设计紧凑型天线阵已成必然。在空间较为狭小时阵元会受到周围阵元的电磁干扰而产生MC效应。本文主要以紧凑型DUCA（如图1所示）为例，分别对其信号衰落相关性和信道容量性能进行分析和比较。

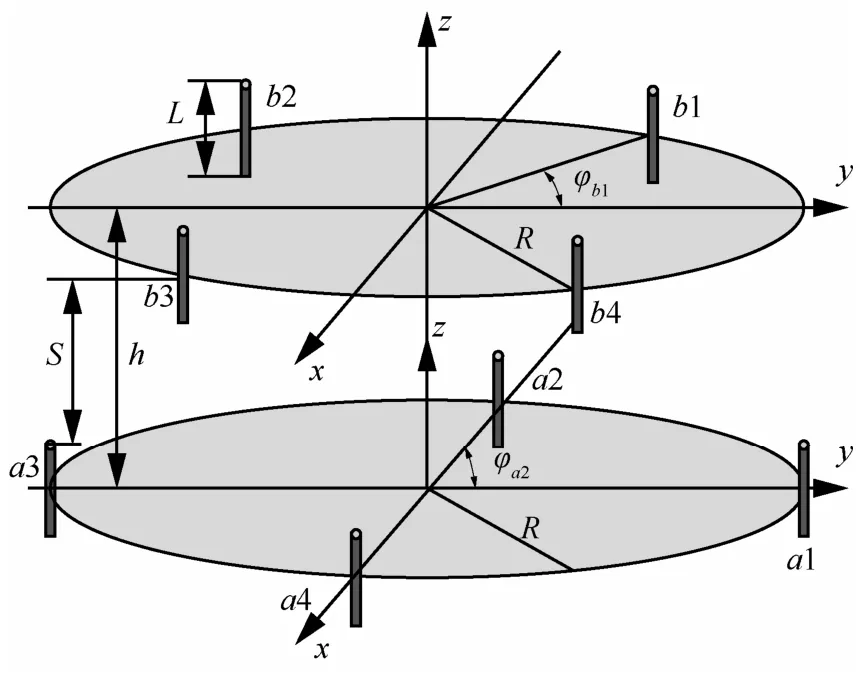
图1 4×4 DUCA多天线MIMO阵列

在图1中，h为DUCA双层阵列间距，R为圆形阵列半径，阵元为线性振子天线长度L，φb1、φa2分别为相应振子天线b1与a2的角位置参数。

2.1 波达衰落信号分布函数

在统计信道建模中，通常是直接对信道参数进行建模来仿真信道中的3种小尺度衰落：时延扩展、多普勒扩展和角度扩展。因此，信号衰落相关性可作为阵元间接收信号的重要参数，其取决于波达信号功率谱（APS，azimuth power spectrum）分布函数和阵元配置模式。在三维空间域中其衰落相关性信道必须被分解为在方位面和仰角面的分析。

通常波达信号APS可定义为截断高斯分布、拉普拉斯分布以及均匀分布等。由于三维空间域信道建模的复杂性，为推导出其理论通用表达式，假设波达衰落信号在方位面和仰角面的APS为相互独立的均匀分布，其概率密度可为[23]

其中，Δ为波达信号分布扩展角。其能量分布是由信号在空间传播中受到信道中各种散射体的反射所引起的，所以，分布函数也可定义为具有双边带分布的其他特征函数，如高斯分布函数或拉普拉斯分布函数。当双边带分布为均匀分布时可以被看成是正负两边分别有均匀分布的波达信号，其概率密度可为

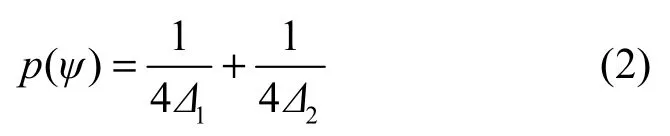
其中，ψ∈[ψ1−Δ1,ψ1+Δ1]∪[ψ2−Δ2,ψ2+Δ2]，Δ1与Δ2分别为波达信号扩展角，ψ1与ψ2分别为双边的中心波达角。扩展角可分别视为方位面（AS，azimuth spread）和仰角面（ES，elevation spread），其分布如图2所示。

图2 双边波达信号APS分布

2.2 互耦效应等效电路模型

根据如图3所示的系统等效模型得知任意两阵元间的MC效应可以用耦合矩阵来描述。如以发射端为例，令vS、vT、i、zT和zS分别为发送端的源电压矢量、发送电压矢量、电路电流矢量、发送端阻抗矩阵和电压阻抗矢量，H2N表示MIMO发送端天线的单元N到接收端天线单元2的信通链路。由图3可得其关系式为

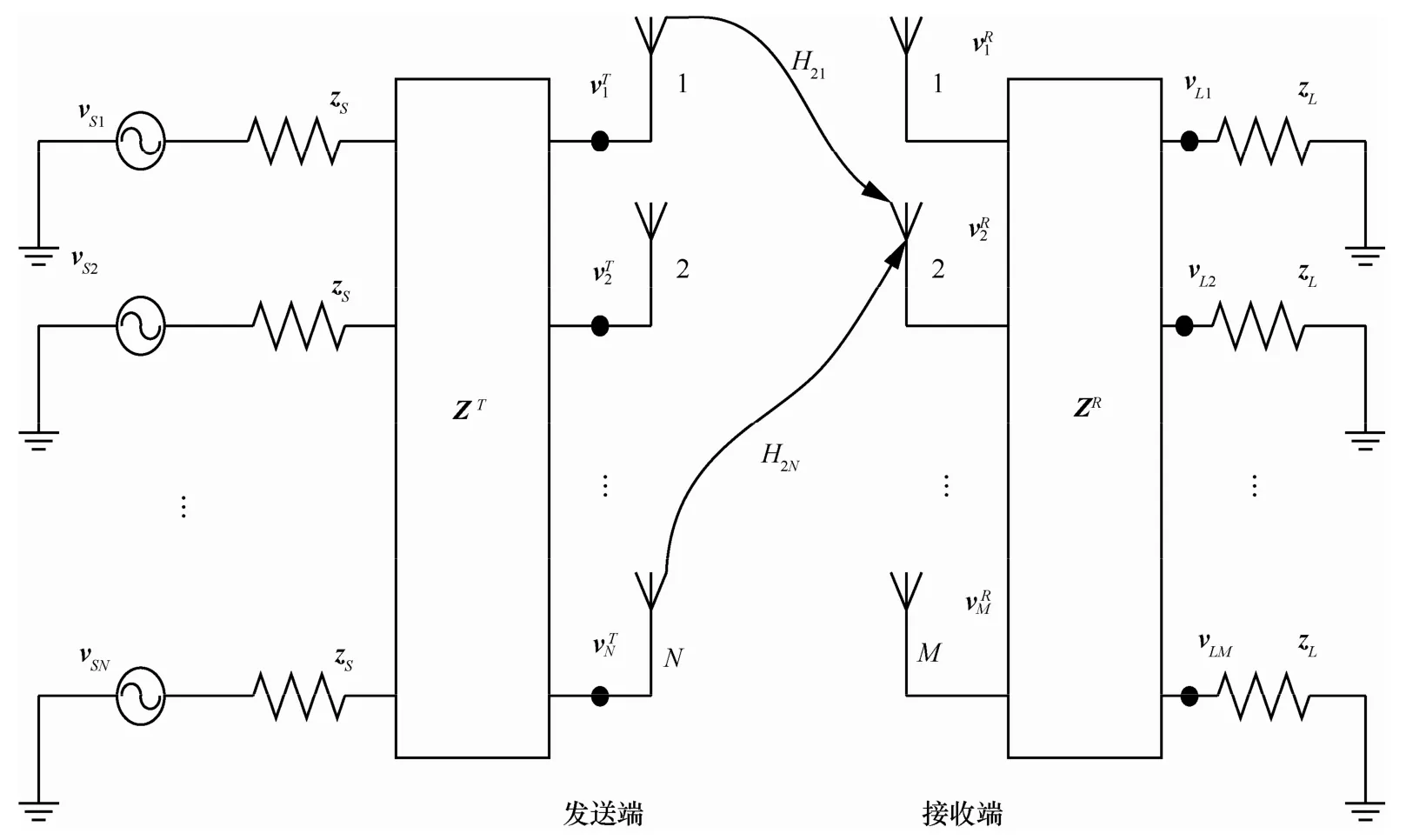
图3 N×M MIMO多天线等效电路模型

其中，zT的元素zmn为发送端第m个天线阵元与第n个天线阵元之间的互阻抗（即MC效应参数）。据研究所知，阵元在不同排列方式下的互阻抗各不相同。由天线互易定理有zmn=znm，于是可以发现zT应为一个对称矩阵，对应的znn表示第n个天线单元的自阻抗，与阵元在自由空间里的输入阻抗相等，其数值大小依赖阵元与其空间结构，可以推导出理论闭式解（分析与计算请详见文献[19～23,27,28]）。由此发射端的等效电路关系式为

对式(3)进行转换可得i=(zT)−1vT，并将其代入式(4)有

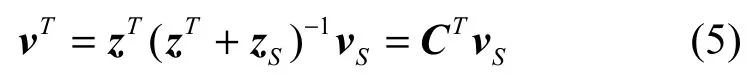
因此，天线阵源电压与端口电压之间的理论关系可以在耦合情况下通过矩阵变换形式获得。在式(5)中CT=zT(zT+z)−1，其中，CT一般称作

S发送端阵列的耦合矩阵。同理可定义vR、zL和vL分别为接收端的天线接收电压矢量、负载阻抗矩阵及其负载上的电压矢量。利用同原理推导接收端得[27]

3 DUCA多天线MIMO系统分析

3.1 阵元间接收信号衰落相关性分析

在图1所示的三维空间域中，当波达信号以其在方位角ψ(0≤ψ≤2π)与仰角θ(0≤θ≤2π)到达MIMO诸天线阵元时，由于阵元间的空间间距与波达信号方向不同会导致诸阵元接收信号的时间不同，接收信号出现相位差。针对如图1所示的MIMO DUCA多天线阵列和坐标系，假设阵列天线数为2M处于坐标面xoy的矢量坐标为rm=[Rcosψl,Rsinψl,0]，其中，参数，R为阵列圆环半径，上层环阵列坐标rm=[Rcos(ψl+ψ0),Rsin(ψl+ψ0),h]。因此，可得矢量信号表达式为

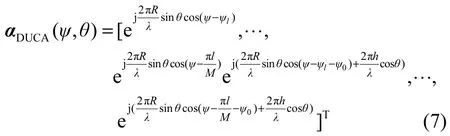
当MIMO天线阵元设计较为紧凑时，阵元所接收的信号会呈现出一定的空间衰落相关性。其表现为信号同时出现包络的峰值或出现衰落的概率比较大。如果出现强相关性将导致信噪比很低，可能使接收信号出现严重失真甚至中断。在不考虑MC效应时，三维空间域任意m与n两阵元间的接收信号空间衰落相关性可表示为[25～28]

其中，p(θ,ψ)为接收端接收多径分量时的APS概率密度函数。在三维空间域中可假设波达信号方位角AOA和仰角EOA是相互独立的，因此，p(θ,ψ)函数可以分解为p(θ)p(ψ)，可由式(1)表示。由DUCA结构可得，阵元m与n间的相关性计算可分为2种情况：1) DUCA同层阵元间相关性计算；2) DUCA异层阵元间相关性计算。把DUCA阵列式(7)和式(1)代入式(8)，经简化可得式(9)和式(17)。

3.1.1 DUCA同层阵元am与an或bm与bn间的衰落相关性

将功率谱式(1)与DVCA矢量信号式(7)中同层阵元两元素代入式(8)，经变换和代简可得同层阵元间的衰落相关式如下。

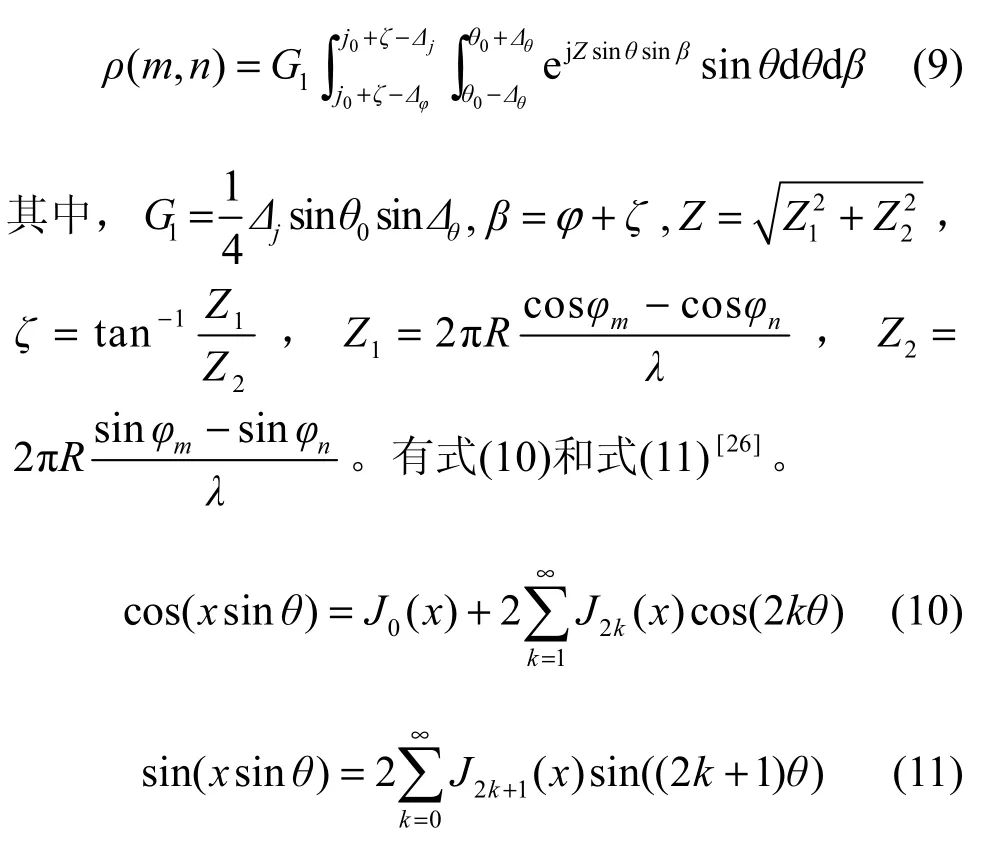
其中，Jk为第k阶Bessel函数。代入式(9)可推导出其函数的实部和虚部分别为

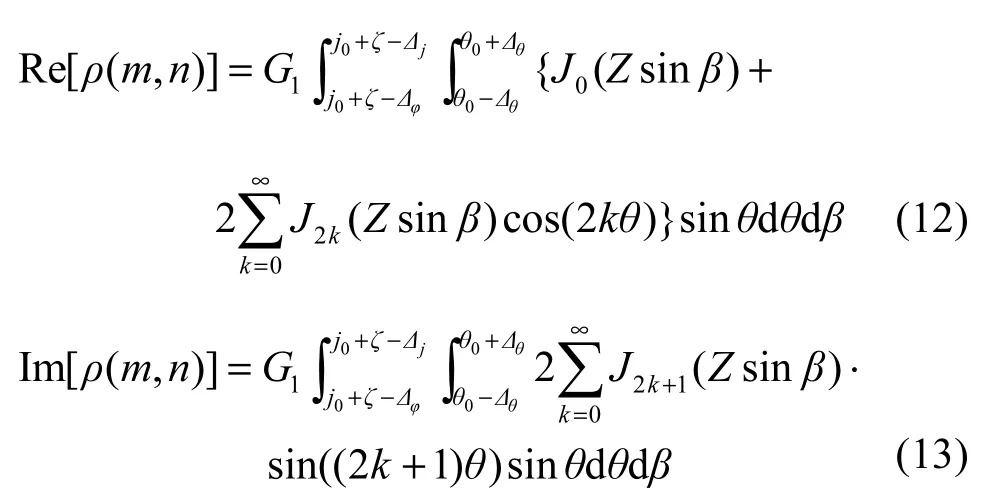
再利用Bessel函数的无穷级数表达式

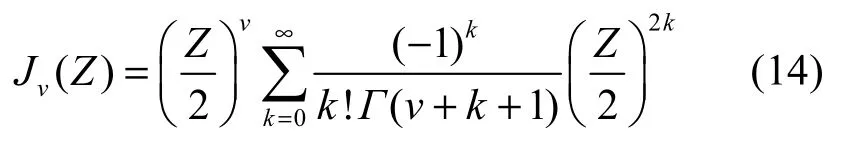
可得

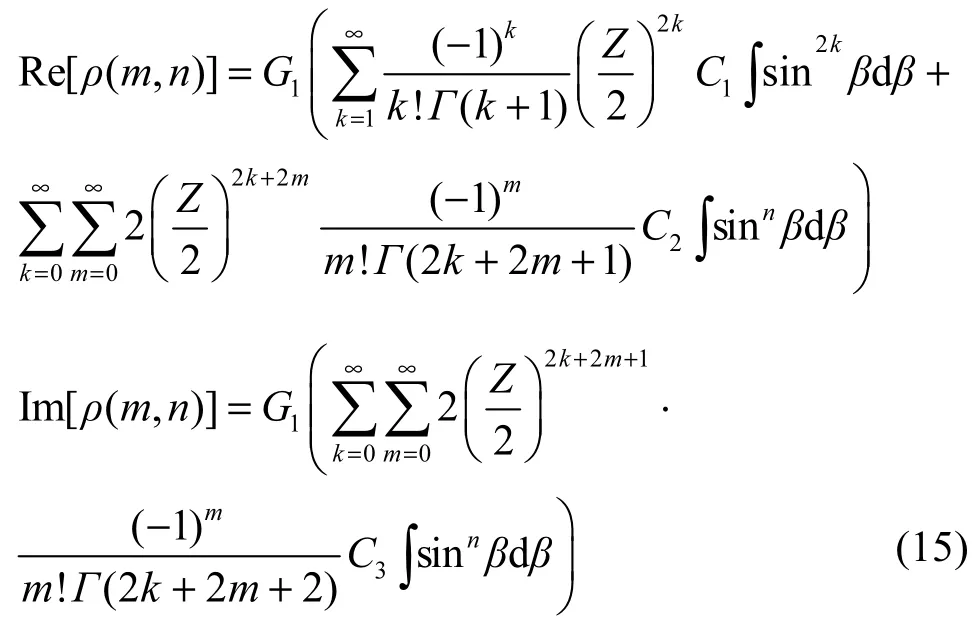
式(15)和式(16)中的积分可由式(26)求解。

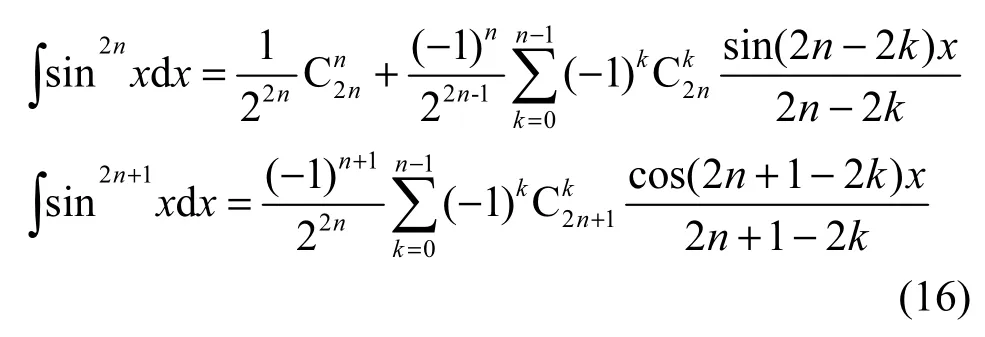
3.1.2 DUCA异层阵元am与bn间的衰落相关性

同理，将式(1)与式(7)中异层两阵元元素代入式(8)，经变换和化简可得异层阵元间的衰落相关性，如式(17)。

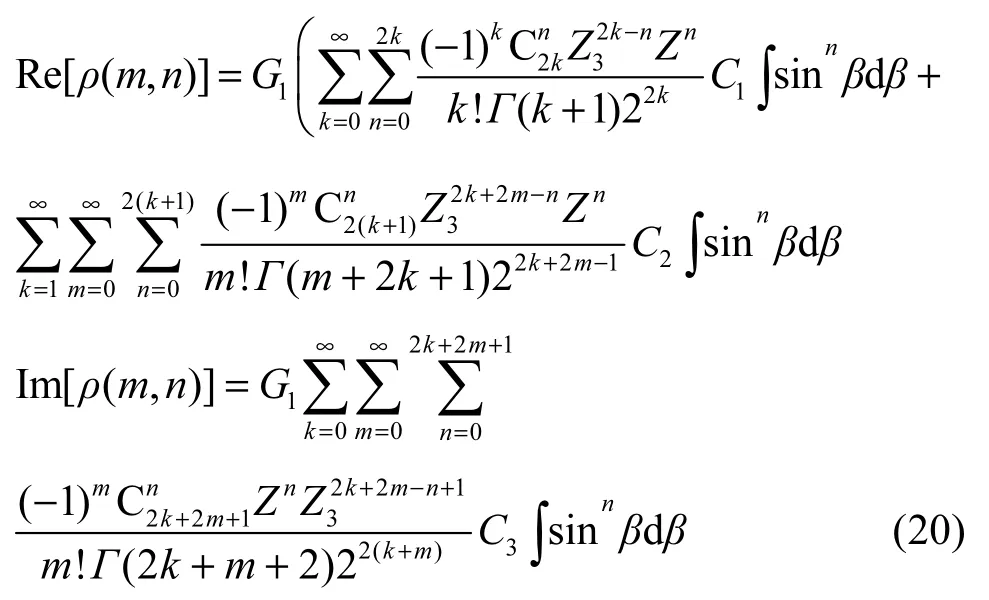
其中，积分可由式(16)求解。另外，C1、C2和C3分别为

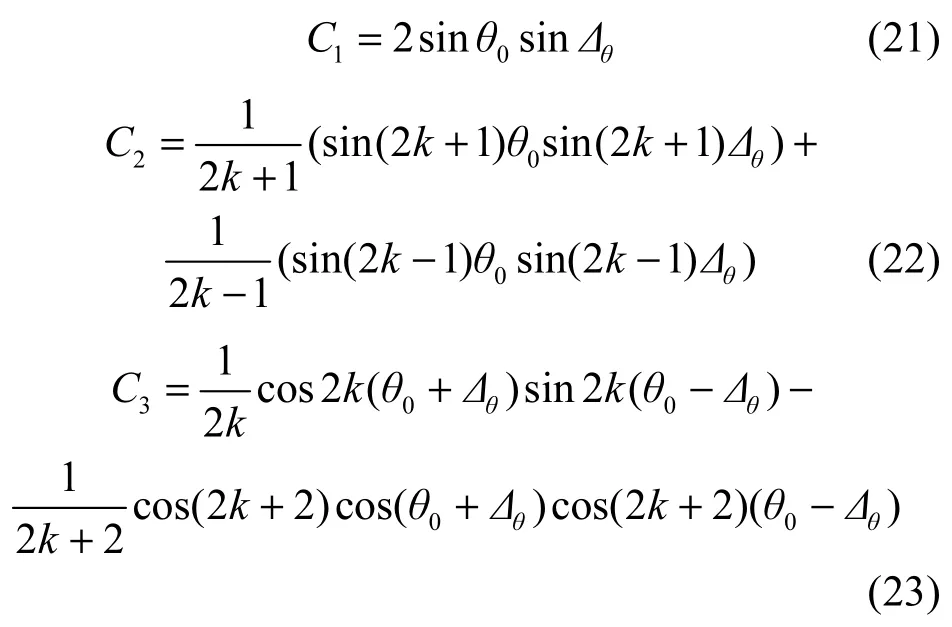
在3.1.1节和3.1.2节中给出了无MC效应时DUCA MIMO任意两阵元间的信号衰落相关性的通用表达式，可以看到其多重积分计算的复杂程度较高。但在分析MIMO信道衰落相关性建模中，可以分别计算两两阵元间的衰落相关性，因此，所有的计算可以在确定波达信号参数以及DUCA阵列参数情况下，通过数值计算方法逐一计算。在研究MC效应的影响时，由等效电路模型可将阵元接收矢量信号式(7)修正为[29,30]

由式(24)替换式(8)中的α(θ,φ)可推导出在MC效应下的信号空间衰落相关性通用表达式。在MC效应下，其衰落相关性表达式将更加复杂。由于MIMO阵列的任意两单元阵元均可看成线性阵ULA。因此，可在如图4(a)所示的简化模型下，首先在不考虑互耦的情况下，二维空间域中两单元ULA接收信号矢量式[27,28]可表示为。在MC效应[29,30]下，式(24)可化简为b(θ)=[c11+c12α1(θ)，c21+c22α2(θ)]，其中，cmn为耦合矩阵CR的第m行第n列元素，且CR为对称矩阵。因此，由式(8)可以得到MC效应下简化ULA两单元阵列的归一化衰落相关性表达式为

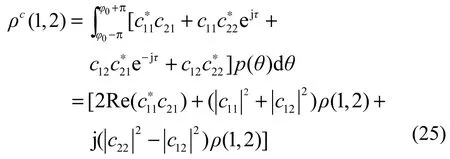
其中，ρ(1,2)是在忽略MC效应时两阵元间的相关系数。由于耦合矩阵CR的对称性还可假设c11=c22=a、c12=c21=b，将其代入式(25)中，化简后可以得到ULA两阵元间相关系数为

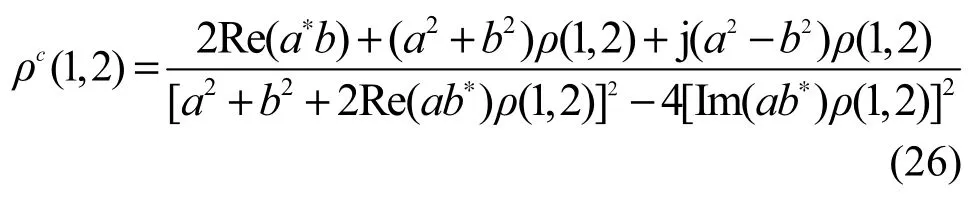
式(25)和式(26)说明在MC效应下阵元间的衰落相关性可由阵列的耦合矩阵和当忽略MC时阵元间的相关系数决定。耦合矩阵可以通过阻抗矩阵、源阻抗矩阵和负载阻抗矩阵得到，因此，由式(26)得到在MC效应下阵元间的衰落相关系数。但是由于其计算复杂，只能逐一采用数值计算法获得其相关性信道矩阵的诸元素，其详细计算请参考文献[27～30]。

3.2 多天线MIMO系统信道容量

多天线MIMO阵列系统性能参数信道容量(channel capacity)决定了通信系统的性能，对其计算和仿真具有重要意义。最早，Foschini等推导了MIMO系统的信道容量C，得到在信号互不相关时C随阵元数增加而线性增大。但是当设备小型化趋势的发展越来越明显时，紧凑型阵列天线得到更多的关注和研究。阵元空间距的降低会增加阵元接收信号衰落的相关性，甚至还受到MC效应的影响。分析中通常利用各态历经容量和互补累积分布函数来描述随机信道容量的统计特性。首先假设基站不具有任何信道信息，则发射功率将均匀分配在每个发射元上，此时一个突发（burst）时间内C的统计均值为[25～28]

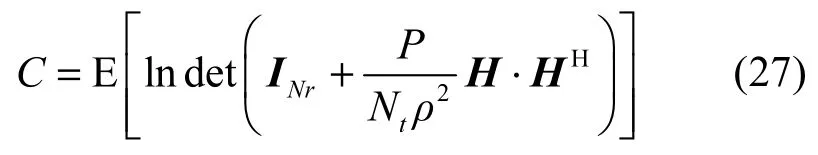
其中，C单位为bit/(s· Hz),INr为单位矩阵，为信道信噪比（SNR）。对于空间衰落相关的多天线MIMO传输信道，其信道矩阵H可利用前面研究的空间信号衰落相关理论以及独立同分布(IID)高斯信道模型，表示为

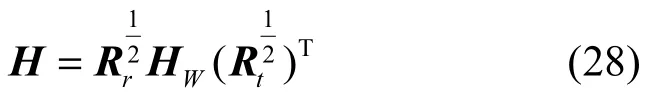
其中，Rr为接收端的MIMO阵元间相关矩阵，Rt为发射端MIMO阵元间相关矩阵，且式(27)和式(28)中上标T和H分别表示矩阵的转置和矩阵的共轭转置算子。因Hw通常假设为独立同分布（IID,independent identically distributed）的复高斯分布信道，其具有以下特殊性质

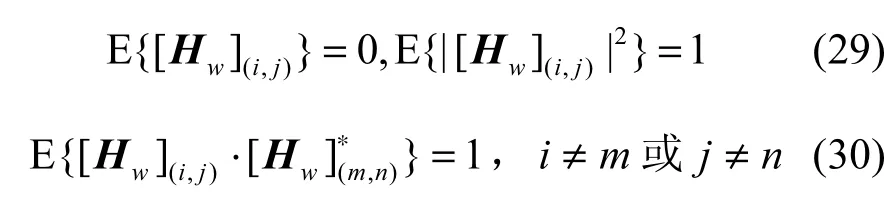
另将式(28)代入式(27)，化简可得

如果发射端天线数量Nt和接收端天线数量Nr相同，且矩阵Rr满秩以及仅考虑单向接收端，即Rt为单位矩阵。如在高信噪比下其信道容量还可近似为

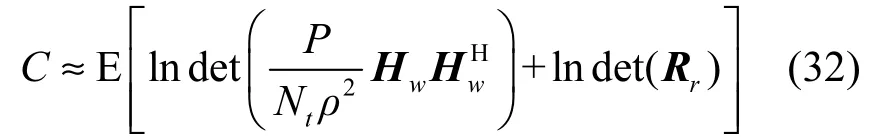
针对MIMO DUCA阵列，可根据前面的分析逐一计算DUCA阵列任意两阵元间信号衰落相关矩阵Rr表示为

其中，矩阵各元素中数字即为DUCA MIMO阵元诸单元编号。由前面的分析式，可利用Matlab软件对MC效应下MIMO系统的信道容量进行数值计算和仿真，即可获得多天线MIMO系统的信道容量等重要参数。由于信道容量是一个随机变化量，分析仿真中将对独立同分布的IID复高斯随机矩阵迭代10 000次，可得系统信道容量的均值结果。

4 分析例与数值结果分析

如图1所示，本文考虑以半波振子为阵元组成DUCA的多天线接收系统。利用上面推导的理论计算式和仿真手段分析天线阵列阵元间的空间接收信号衰落相关系数，进而可分析系统的信道容量C，并与ULA和UCA天线阵列性能相比。在计算和仿真中采用的MIMO系统参数LIST如下：1) 阵元选择为半波振子；2) DUCA天线阵元数量为4×4阵元；3) 取圆环半径R=2λ；4) 信噪比为20 dB；5) 源电压阻抗和负载电阻取值均为75Ω，可获得与半波振子的最优阻抗匹配。如图1所示的DUCA多天线MIMO阵列配置中诸阵元按照不同位置，其任意两阵元的相对位置可以看成如图4所示的平行放置、共线放置和梯式放置结构，其中，d为平行天线阵列单元间距，s为共线天线阵列单元间距，h为共线单元基点的纵向间距。

图4 平行、共线与梯式阵元放置结构

4.1 阵元间信号衰落相关性

图5为梯式平行天线之间的互电阻和互电抗的计算结果。d为天线间水平距离，h为天线间垂直距离。其结果与平行和共线放置的互阻抗变化趋势相同，且呈现三角波形振荡衰落趋势，并随垂直间距和水平间距的增大最终趋于零。在d或h分别为0时，梯式放置演变成平行和共线放置方式。另外随着阵元间距增大阵元间互电阻和互电抗最终趋近于0，其物理意义解释为当阵元间距离增大到一定程度时，MC效应将最终消失。

图5 梯式放置天线阵元之间互阻抗

图6 ULA、UCA和DUCA相邻阵元间衰落信号相关性

图6表示ULA、UCA和DUCA阵列分别在有和无MC效应的情况下，相邻阵元间信号空间衰落相关性与参数R之间的关系。随着参数R的增加，信号的空间衰落相关性减小。在有MC效应时的相关性曲线以无MC衰落相关性曲线为中心波动，说明天线阵元的空间位置对此有较大影响。仿真结果表明随着阵元间距的增大，曲线波动的幅度越来越小，并逐渐与无MC衰落相关性曲线趋于重合。其物理过程解释，随着天线阵元间距增大而使互耦效应减弱，因此，对衰落相关性的影响也会逐渐变小。另外，发现在不同天线阵列下的衰落相关性也具有较大区别。在相同参数下ULA阵元间的相关性最大，而DUCA阵元最小。其结果得益于在DUCA阵列中，形成了一种梯形放置结构[1～3]而使两阵元间的相对间距增大。因此，当阵元间距较大时及在一些特殊点上，MC效应会降低信号衰落相关性，而提高MIMO系统的性能。因此，阵列结构设计对于MC效应具有较大的影响，将会对阵元间衰落相关性的影响起到决定作用。

4.2 DUCA MIMO信道容量

图7表示有相同天线阵元数时ULA、UCA和DUCA阵列的信道容量与参数R之间的关系。当参数增大时，信道容量先增加后趋于稳定。在较小即时，MC效应会导致信道容量增加。而在较大时，互耦效应影响会使信道容量减小。随着增大而使阵元间的互耦效应减弱，最终逐渐使信道容量趋于相同值。另外，UCA和DUCA阵列的信道容量均比ULA大，且MC效应对UCA和 DUCA的影响较ULA小。原因为阵元以面和空间设置代替了ULA的线性设置，从空间上增大阵元间距而减小了空间信号衰落相关性，且又减轻了阵元间的MC效应使系统性能得到提高。

图8为MIMO信道容量与波达信号的方位角AOA和仰角EOA之间的关系。当终端为ULA阵列时，信道容量小于UCA和DUCA阵列并且波动较大，说明波达信号方向对ULA阵列接收性能影响较大，且信道容量以为对称且达到最小值。随着AOA的增加或者减小，容量均呈现出先增加后减小的趋势。在仰角面中信道容量在时达到最大值，且随EOA的增大或者减小，容量均呈现先减小后增加的趋势。图9为MIMO信道容量与波达信号的角扩展参数AS和ES之间的关系。结果显示随着参数AS或ES的增加，MIMO系统的信道容量增加，且UCA与DUCA阵列的信道容量交错变化。但ULA阵列的信道容量最小。比较图8与图9可知在参数AS或ES较大(≥30°)时，波达信号方向AOA和EOA对信道容量的影响比较明显。

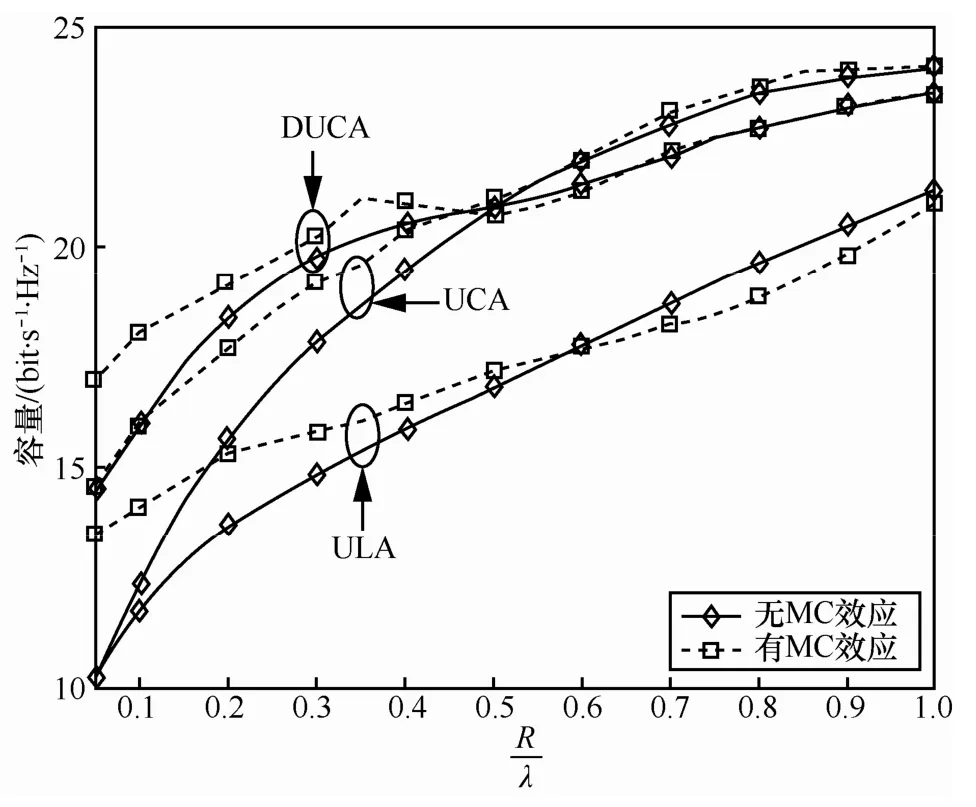
图7 ULA、UCA和DUCA多天线阵列信道容量

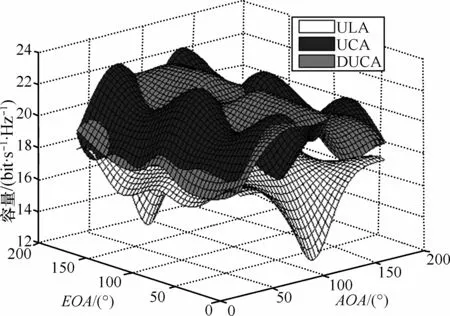
图8 EOA和AOA对MIMO多天线信道容量的影响

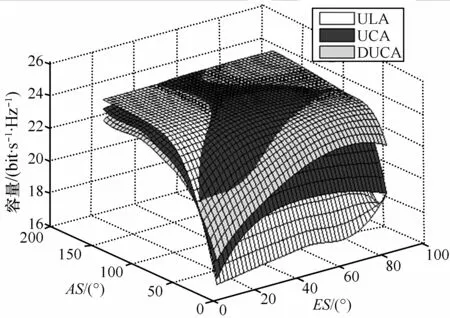
图9 ES和AS对MIMO多天线信道容量的影响

5 结束语

针对非频率选择性瑞利衰落信道，本文建立和应用了多天线MIMO阵列在互耦效应下的等效网络模型，推导出三维空间域下的DUCA多天线阵列衰落相关性的通用表达式，阐明MC效应下信号衰落相关性的机理，并以DUCA阵列为例，分析了其互耦相关性的波动情况以及MIMO信道容量。由此可知空间设计和MC效应对阵元间信号衰落相关性的影响起决定性作用，在MC影响下，DUCA和UCA的容量均比MIMO大，而且波达信号的方位角和仰角相比角度扩展AS和ES对信道容量的影响较大，且MIMO信道容量的大小主要取决于波达信号的方位。该信道建模方案简单且使用灵活，DUCA多天线MIMO阵列模型具有较好的性能。

[1]克劳斯,马赫夫克.天线[M].章文勋,译.北京:电子工业出版社,2005:11-14.KRAUS J D,MARHEFKE R J.Antennas[M].ZHANG W X translation.Beijing:Publishing House of Electronics Industry,2005:11-14.

[2]GESBERT D,SHAFI M,SHIU D S,et al.From theory to practice:an overview of MIMO space-time coded wireless system[J].IEEE Journal on Selected Areas in Communications,2003,21(3):281-302.

[3]郭强,周希朗,张伟炯,等.天线匹配对莱斯信道下紧凑MIMO系统性能的影响[J].电波科学学报,2009,24(6):1009-1013.GUO Q,ZHOU X L,ZHANG W J,et al.Effect of antenna matching on compact MIMO system performance in Rician fading channels[J].Chinese Journal of Radio Science,2009,24(6):1009-1013.

[4]TELATAR I E.Capacity of multi-antenna Guassian channels[J].European Transaction on Telecommunications,1999,10(6):585-595.

[5]FOSCHINI G J,GANS M J.On limits of wireless communications in a fading environment when using multiple antennas[J].Wireless Personal Communications,1998,6(3):311-335.

[6]ITU.Guidelines for evaluation radio transmission technologies for IMT-2000[S].ITU recommendation M1225,ITU,Tech.Rep,2000.

[7]LUCENT,NOKIA,SIEMENS,et al.A standardized set of MIMO radio propagation channels[R].Technical Report,3gpp tsd r1-01-1179,2011.

[8]SVALESSON T,RANHEIM A.Mutual coupling effects on the capacity of multi-element antenna systems[C]//IEEE International Conference on Acoustics,Speech,and Signal Processing,2001:2485-2488.

[9]WALLACE J W,JENSEN M A.The capacity of MIMO wireless systems with mutual coupling[C]//IEEE Vehicular Technology Conference.2002:696-700.

[10]DANDEKAR K R,HEATH R W.Modeling realistic electromagnetic effects on MIMO systems capacity[J].Electron Lett,2002,38(25):1624-1625.

[11]JUNGNICKEL V,POHL V,HELMOLT.C.Capacity of MIMO systems with closely spaced antennas[J].IEEE Communications Letters,2003,7(8):361-363.

[12]WALDSCHMIDT C,HAGEN J V,WIESBECK W.Influence and modeling of mutual coupling in MIMO and diversity systems[J].IEEE Antennas and Propagation Society International Symposium,2002,3(8):190-195.

[13]李纪,李晓舟,张尔扬.互耦对MIMO信道空间相关特性的影响[J].国防科技大学学报,2006,28(4):73-77.LI J,LI X Z,ZHANG E Y.Impact of mutual coupling on the spatial correlation of MIMO channel[J].Journal of National University of Defense Technology,2006,28(4):73-77.

[14]SVANTESSON T,RANHEIM A.Mutual coupling effects on the capacity of multielement antenna systems[C]//IEEE International Conference on Acoustics,Speech,and Signal Processing,Salt Lake City,2001,2:2485-2488.

[15]FLETCHER P N,DEAN M,NIX A R.Mutual coupling in multi-element array antennas and its influence on MIMO channel capacity[J].IEEE Electronics Letters,2003,39(4):342-344.

[16]JUNGNICKEL V,POHL V,HELMOLT V C.Capacity of MIMO systems with closely spaced antennas[J].IEEE Communications Letters,2003,7(8):361-363.

[17]TSAI J A,WOERNER B D.The fading correlation function of a circular antenna array in mobile radio environment[C]//IEEE Global Telecommunications Conference.San Antonio ,USA.2001,5:3232-3236.

[18]KUCHAR A,ROSSI J P,BONEK E.Directional macro-cell channel characterization from urban measurements[J].IEEE Trans Antennas and Propag,2000,48(2):137-146.

[19]FULH J,ROSSI J P,BONEK E.High-resolution 3-D direction-of-arrival determination for urban mobile radio[J].IEEE Trans Antennas and Propag.1997,45(4):672-682.

[20]SALZ J,WINTERS J H.Effect of fading correlation on adaptive arrays in digital mobile radio[J].IEEE Trans Veh Technol,1994,43(4):1049-1057.

[21]JIANN A T,BUEHERE R B,WOERNER B D.Spatial fading correlation function of circular antenna arrays with Laplacian distribution energy[J].IEEE Commun Lett,2002,6(5):178-180.

[22]QU S,YEAP T.A three-dimensional scattering model for fading channels in land mobile environment[J].IEEE Transactions on Vehicular Technology,1999,48(3):765-781.

[23]赵勇洙,金宰权,杨元通,等.MIMO-OFDM无线通信技术及MATLAB实现[M].孙楷,黄威译.北京:电子工业出版社,2013:14-17.ZHAO Y Z,JIN Z Q,YANG Y T,et al.MIMO-OFDM wireless communications with Matlab[M].SUN K,HUANG W Translation.Beijing,Publishing House of Electronics Industry,2013:14-17.

[24]SHIU D S,FOSCHINI G J,GANS M J.Fading correlation and its effect on the capacity of multi-element antenna systems[J].IEEE Transactions on Communications,2000,48(3):502-513.

[25]KRAUS J D,MARHEFKA R J.Antenna for all applications[M].Upper Saddle River,NJ:McGraw Hill.

[26]GRADSHTEYN I S,RYZHIK I M.1994 Table of Integrals,Series and Products[M].5th ed San Diego(CA:Academic).

[27]Chen J.F,ZHOU J.Effect of mutual coupling on the spatial correlation between the elements of antenna array[J].Journal of Chongqing University of Posts and Telecommunications,2012,24(4):420-425.

[28]ZHOU J,CHEN J.F,QIU L,et al.Effects of mutual coupling and antenna correlation on MIMO in three dimensional spatial channel models[J].Journal of Communications,2012,33(6):1-10.

[29]LI X,NIE Z.P.Mutual coupling effect on the performance of MIMO wireless channels[J].IEEE Antennas and Wireless Propagation Letters,2004,3(1):344-347.

[30]Li X,NIE Z P.Mutual coupling effects of MIMO wireless channels[C]//IEEE Conf on Microwave and Millimeter Wave Technology.2004:150-153.

邵根富（1962-），男，浙江宁波人，杭州电子科技大学教授，主要研究方向为无线通信理论、信号处理与自动控制等。

姚颖莉（1988-），女，江苏徐州人，南京信息工程大学博士生，主要研究方向为移动通信理论和多天线MIMO信道建模等。

周杰（1964-），男，四川泸州人，南京信息工程大学教授、博士生导师，日本国立新泻大学访问教授，主要研究方向为移动通信理论、无线传感网络和无线接入网等。

菊池久和（1951-），男，日本新泻人，日本国立新泻大学教授、博士生导师，南京信息工程大学名誉教授、博士生导师，主要研究方向为信号处理和通信理论等。

Performance analysis of MIMO DUCA multiple antenna system

SHAO Gen-fu1,YAO Ying-li2,ZHOU Jie2,3,HISAKAZU Kikuchi3
(1.Dept.of Automation,Hangzhou Dianzi University,Hangzhou 310018,China;2.School of Electronic &Information Engineering,Nanjing University of Information Science and Technology,Nanjing 210044,China;3.Dept.of Electronic and Electrical Engineering,Niigata University,Niigata 950-2181,Japan)

A MIMO multi-antenna system of compact double uniform circular array (DUCA) in three dimensional directional frequency non-selective Rayleigh fading channel was analyzed and investigated.Equivalent network model of MIMO multi-antenna array considering MC effect was established,general expressions of correlations were derived and the relationship between correlations with and without MC was classfied.Then,the results were compared with general uniform linear array (ULA) and uniform circular array (UCA).It was concluded that the deployment of antennas plays a decisive role in correlations between antennas.The research has a good sense on designation of spatial massive MIMO multi-antenna array and system optimization.

multiple input multiple output antenna array,double uniform circular array,mutual coupling effect,signal fading correlation

s:The National Nature Science Foundation of China (No.61471153),Scientific &Technological Support Project of Jiangsu University (No.14KJA510001)

TN911.6

A

10.11959/j.issn.1000-436x.2016226

2016-01-05；

2016-07-08

国家自然科学面上基金资助项目（No.61471153）；江苏省高校自然科学重大基金资助项目（No.14KJA510001）