基于动态三角剖分的潜在冲突筛选方法

苏志刚, 符笑娴, 郝敬堂

(1. 中国民航大学中欧航空工程师学院, 天津 300300; 2. 中国民航大学智能信号与图像处理天津市重点实验室, 天津 300300; 3. 福建通航航空产业有限公司, 福建 福州 350000)



基于动态三角剖分的潜在冲突筛选方法

苏志刚1,2, 符笑娴1,3, 郝敬堂1

(1. 中国民航大学中欧航空工程师学院, 天津 300300; 2. 中国民航大学智能信号与图像处理天津市重点实验室, 天津 300300; 3. 福建通航航空产业有限公司, 福建 福州 350000)

摘要：围绕动态Delaunay三角剖分(dynamic delaunay triangulation,DDT)方法难以对空域动态三角剖分中产生的反转三角形实现稳定局部更新问题,提出以顺序的点删除与点增加的局部更新方式替代反转三角形的局部更新方式的改进方法。实验结果表明,改进的DDT方法获得的潜在冲突航空器数目与空域内航空器密度无关,且具有更低的局部更新时间复杂度和稳健性。改进的DDT方法更稳健,更适用于空管指挥系统的潜在冲突筛选任务。

关键词：空中交通管理; 冲突检测; 动态Delaunay三角剖分; 移动点集; 动态更新

0引言

近年来,随着经济的飞速发展,民用航空器总量迅速增加,使得航空器运行空域变得越来越拥挤,加之人为、天气、故障等因素的影响,航空器间空中冲突、甚至空中相撞风险日益增大。例如:1996年沙特与哈萨克斯坦的客机在空中相撞,导致300多人遇难。2002年德国与俄罗斯的客机在空中相撞,机上70多人遇难。

地面空管指挥系统中的短期冲突告警(short term conflict alert,STCA)子系统[1]可以逐对判断航空器间突破安全间隔标准的风险[2-4],对存在危险接近或相撞可能性的航空器给出相应的警示,协助管制员对空域内航空器进行调度、管理。随着航空器数目的增大,STCA子系统计算复杂度将以平方量级增长。为有效地降低系统计算复杂度,提高短期冲突检测的可靠性、实时性,STCA子系统进行冲突检测前需要对潜在冲突进行筛选[5-6]。

距离门限法是一种经典的潜在冲突筛选方法,以航空器间的距离为准则筛选潜在冲突对,可以在一定程度上减少STCA负荷。然而随着空中航空器数量的增多,特别是在终端区域,航空器密度加大,以航空器间距离为基础的距离门限法需要跟踪更多的潜在冲突对。近年来,有学者将图形学的Delaunay三角剖分技术应用于潜在冲突筛选处理[6-9],使得潜在冲突对筛选数量与空域内航空器密度关系不大,从而降低了系统计算复杂度与空域内航空器数目之间的关联。

空域内航空器的移动特征,使学者将移动点的Delaunay三角剖分技术应用于空管领域[7-10]。文献[7]将快拍式Delaunay三角剖分(snapshot Delaunay triangulation,SDT)用于潜在冲突筛选。SDT方法需要周期地根据航空器位置信息进行Delaunay三角剖分,没有利用刷新前后航空器位置关系的继承性,因此,其计算复杂度较高。动能Delaunay三角剖分(kinetic Delaunay triangulation,KDT)方法[8,10]根据移动点的速度、位置信息,以连续时间的方式预测三角网格发生拓扑变化的时刻,仅在发生拓扑变化的时刻对发生拓扑变化的局部进行三角剖分更新。KDT方法解决了空间三角剖分的拓扑结构的继承问题,可以有效地降低系统预选的复杂度,但对拓扑结构变化时刻的解算会引入额外计算量,当存在大量拓扑变化时,相应引入的复杂度较大[11-12]。动态Delaunay三角剖分(dynamic Delaunay triangulation,DDT)方法[9]检测在离散时间点处的拓扑变化,对局部进行三角剖分更新。DDT方法与KDT方法相比,减少了拓扑结构变化时刻解算的计算量。文献[9]所提出的DDT方法可以有效地解决航空器进入、离开或位置更新等情况下的空域Delaunay三角剖分的动态更新问题,但当空域Delaunay三角剖分的拓扑结构发生较大变化时,如存在反转三角形的情况时,该方法无法有效地完成空域Delaunay三角剖分的局部更新,甚至可能陷入死循环[13]。

本文将在文献[9]的DDT方法基础上,针对反转三角形的存在导致DDT方法不稳定问题,提出一种可以有效解决反转三角形存在时的局部更新的方法,使得改进的DDT方法更适于应用到短期冲突检测的筛选处理中。

1空域Delaunay三角剖分

当航空器在航路上飞行时,航空器间的短期冲突检测主要是针对同一高度层的航空器进行的,因此将空域中同一高度层的航空器看作离散点集,并依据Delaunay三角剖分准则,使得剖分后三角形的外接圆内不包含除顶点处航空器以外的任意航空器,形成以航空器为顶点的不均匀的三角形网格,如图1所示。由图1可见,空域内的航空器以最近邻的三个航空器形成三角形,连接航空器的线段(三角形的边)均不相交,且与远处的航空器不直接发生联系。这个特点与空管指挥系统中的潜在冲突航空器的特征相似,因此,可以利用Delaunay三角剖分所获得的空域内航空器的拓扑结构,并以此作为潜在冲突筛选手段。

图1　空域Delaunay三角剖分

空域Delaunay三角剖分的初始化就是根据系统中航空器的初始位置,按照静态离散点集的方式对其进行Delaunay三角剖分。空域Delaunay三角剖分的初始化可以采用分治算法、逐点插入法、三角网生长法等经典算法实现,本文采用逐点插入法。逐点插入法的起始需要获得包含全部离散点集的凸多边形,然后采用逐点插入的方式进行Delaunay三角剖分。为降低寻找凸多边形的复杂度,可将关注空域的四角设置4个虚拟点,进而形成包含空域全部航空器的凸多边形,而且执行逐点插入法即可完成空域的初始Delaunay三角剖分。

2拓扑结构的动态更新

空域内航空器的运行将引起空域三角网格的改变,由于航空器的轨迹的连续性,航空器间的拓扑结构呈现出缓变特点,使得空域Delaunay三角剖分具有相对稳定性。对于空域的三角网格,在缓变过程中出现不满足Delaunay三角剖分准则的三角网格也只发生在局部的,而非整体性的。DDT方法就是根据空域内航空器的增、减及位置变化,对空域的初始Delaunay三角剖分进行局部动态更新,实现空域Delaunay三角剖分的动态更新的目的。

空域内出现新增航空器时,可以采用点插入技术对空域内局部Delaunay三角剖分进行更新[14]。首先检索出外接圆包含新增航空器的三角形,删除相应三角形,形成凸多边形。将凸多边形的顶点与新增航空器点相连接即完成局部Delaunay三角剖分。假设需要判断出现在点P4处的航空器是否位于ΔP1P2P3的外接圆内。根据点P1、P2、P3和P4的横、纵坐标xi和yi(i=1,2,3,4)可以定义矩阵

(1)

假设P1、P2、P3为逆时针排列,若C1234的行列式|C1234|>0,则点P4在ΔP1P2P3的外接圆内,若行列式|C1234|<0,则点P4在ΔP1P2P3的外接圆外[15]。由于三角形顶点的排列顺、逆时针判断较为不便,因此引入辅助点P5,使其位于P1P2的延长线上,且坐标为(x5,y5)=(2x2-x1,2y2-y1)。显然辅助点P5一定位于ΔP1P2P3的外接圆外。所以,若点P4在ΔP1P2P3的外接圆内,判断准则

(2)

必然成立。

若空域内某航空器飞离时,由于该点的消失,使得空域Delaunay三角剖分的局部出现空腔,而且该空腔有可能不是凸多边形,直接对其三角剖分可能出现交叉的边。可以采用凸耳权值的点删除算法进行维护[16]。

航空器运动引起空域三角形缓变,出现局部三角形不再满足Delaunay三角剖分准则,即原有的外接圆内出现了其他航空器。进入三角形外接圆的航空器与该三角形构成两个共边三角形结构,利用局部优化程序(local optimization procedure,LOP)可以实现局部拓扑更新[13,17]。

3对反转三角形的局部更新

前面的DDT方法可以实现对空域内航空器间拓扑结构的基本动态维护,然而,当存在位置变化较大的航空器、或存在尺度较小的三角形时会出现三角形反转的可能性。三角形反转即为该三角形的顶点排列的顺、逆时针顺序发生改变,如图2所示。图2中点A在前后两个时刻的位置变化,使得三角网格顶点ABC由顺时针方向转变为逆时针方向。反转ΔABC有存在使其周边的三角形不再满足Delaunay三角剖分准则,如图2(b)的阴影区域。采用LOP处理已经无法获得正确的Delaunay三角剖分,需要新的局部动态维护方案。

图2　反转三角形网格对局部的影响

实现对反转三角形的局部拓扑更新的前提是需要定位反转三角形。判断是否存在反转三角形的基础是检测三角形顶点的排列方向是否发生改变。定义在第n时刻三角网格顶点矩阵

(3)

式中,xi(n)和yi(n)分别为三角形第i(i=1,2,3)个顶点Pi在第n时刻的横、纵坐标。如果三角形的顶点P1、P2和P3是按顺时针排列,则三角形顶点矩阵T(n)的行列式|T(n)|<0,反之则|T(n)|>0。因此,三角形顶点排列方向是否发生改变可由式(4)判断。

(4)

式(4)表明根据相邻时刻的三角形顶点矩阵行列式的值是否异号可以判断三角形是否为反转三角形。遍历空域内全部三角形,检索出所有反转三角形。

反转三角形确定后,还需要进一步确定反转点。反转点是指进入反转三角形的共边三角形内部的反转三角形的顶点,如图2所示的顶点A。反转点邻近离散点的局部拓扑结构发生急剧变化,需要进行重新Delaunay三角剖分。对于反转三角形,可以存在3个与其共边的三角形,因此需要根据反转点与共边三角形的关系确定反转点。

判断某点在三角形内部的方法可采用内角和法、同向法、重心法等方法,本文采用计算效率较高的重心法。假设判断ΔP1P2P3的顶点P1是否为反转点,点P1所对应的共边三角形为ΔP2P3P4,需要判断下一时刻点P1是否落在ΔP2P3P4内。定义矩阵

(5)

(6)

(7)

利用式(5)～式(7)可得

(8)

(9)

式中,(·)-1表示求倒数操作。因此,若点P1落在共边ΔP2P3P4内需满足

(10)

若式(10)不成立,则说明点P1未落在共边ΔP2P3P4内。

由于航空器间安全距离的限制,航空器的单次位置变化量通常小于Delaunay剖分后的三角形尺度,反转点一般只落在反转三角形的共边三角形内。反转点在短时间内跨越多个三角形,落在非共边三角形内的可能性非常小,本文不予考虑。

由于反转点的存在,反转三角形周边的部分三角形需要重新进行局部Delaunay三角剖分。本局部的Delaunay剖分等价于原来所处位置消失了一个点,同时在反转点的共边三角形内增加一个新点。因此,对于反转三角形的局部更新可以用删除点与增加点的方式进行局部更新。由图2(b)可见,反转点A在共边三角形中按增加点进行更新时,可能会影响删除点区域的剖分,因此,反转三角形的局部更新需要按删除点、增加点的顺序进行更新。

4仿真实验

本部分将采用数值仿真的方法比较改进的DDT方法与SDT方法、距离门限方法作为潜在冲突筛选方法的筛选效率。根据空管指挥系统的实际指标,仿真实验中考虑1 000km×1 000km空域。空域内航空器的位置及速度以随机方式产生,其中航空器的位置分布服从以空域中心为的二维高斯分布,航空器速度大小服从700～1 000km/h内的均匀分布,速度方向服从360°方向的均匀分布。假设空域内的航空器以匀速直线运动。

首先,分析空域内航空器数目对不同筛选方法初始化时间及筛选潜在冲突航空器数量的影响。将空域内航空器数目由20加逐步增加到500架,在每个数据点执行100次蒙特卡罗实验,分别统计改进的DDT方法、SDT方法、距离门限法在以50km和100km为门限时完成首次潜在冲突航空器检测所需的时间和潜在冲突航空器的平均数量,如图3所示。

图3　空域内航空器数量对筛选方法初始化的影响

如前所述,改进的DDT方法和SDT方法筛选潜在冲突航空器是利用空域航空器的Delaunay三角剖分实现的。这两种方法确定的潜在冲突航空器的平均数量是指空域内航空器所在三角剖分中的边的平均数。距离门限法是计算两两航空器之间的距离,通过与相应门限值比较来确定是否存在潜在冲突对。因此,距离门限法的初始化时间与门限值无关,改进的DDT方法和SDT方法均需要完成空域航空器的Delaunay三角剖分,所以两者的初始化时间也相同,如图3(a)所示。由如图3(a)还可以看出,随着空域内航空器数目的增加,所有方法的初始化时间均增加,而且距离门限法时间增长速度明显快于改进的DDT方法和SDT方法。当空域内航空器数目较少时,距离门限法的效率优于改进的DDT方法和SDT方法,但空域内航空器数目增加到一定数量时,改进的DDT方法和SDT方法将优于距离门限方法。

在潜在冲突航空器筛选方面,由图3(b)可见,距离门限方法所筛选出的潜在冲突航空器数目与空域内航空器数目及门限大小有关。空域内航空器数目的增大,导致筛选出的潜在冲突航空器平均数呈线性增长,而且增长的速率与门限有大小有关。在图3(b)中,航空器数目的增大,导致空域内航空器的密度加大,由此可以推断,在航空器密集区域,如终端区域等,采用距离门限方法筛选出手潜在冲突航空器数量将显著增加。由图3(b)可见,改进的DDT方法和SDT方法所筛选出的潜在冲突航空器数目约为3,并且与空域内航空器的数目或航空器的密度无关,因此,更适宜使用在航空器密集区域的短时冲突告警检测的筛选处理。

其次,分析空域内增、减航空器对筛选方法效率的影响。考虑空域内已有航空器200架,采用逐一增加的方式将航空器数量增加到225架,考察每增加一架航空器时,每个筛选方法对时间的消耗。同样,在每个数据点处进行100次蒙特卡罗实验。实验结果如图4所示。由图4可见,距离门限方法的刷新时间随着航空器数目的增加而增大,这与图3(a)结果一致。随着航空器数目的增加,SDT方法的时间消耗有些许增加,这是因为每次空域Delaunay三角剖分的离散点数增加所致。改进的DDT方法的时间消耗基本不变,且时间消耗最低。每次增加1个目标,对于改进的DDT方法只是对空域Delaunay剖分的局部进行更新,因此,每次引入的计算量基本相当。

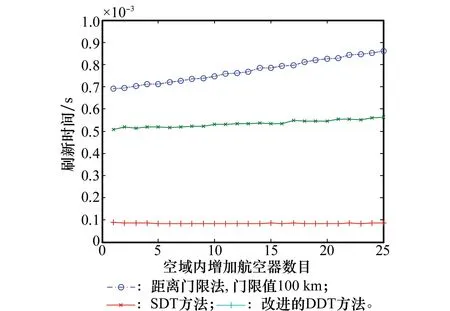
图4　空域内航空器数量逐一增加对刷新时间的影响

相类似地考虑空域内航空逐一删除对筛选方法效率的影响。仍然假设空域内已有航空器200架,采用逐一删除方式将航空器数量减少到175架,考察每删除一架航空器时,每个筛选方法对时间的消耗。同样,在每个数据点处进行100次蒙特卡罗实验。实验结果如图5所示。与图4相比较,距离门限方法的刷新时间与航空器数目相关,SDT方法的时间消耗也与航空器数目有关,但受影响程序不显著,改进的DDT方法的时间消耗基本不受航空器数目的影响,且时间消耗最低。

图5　空域内航空器数量逐一减少对刷新时间的影响

再考虑同时增加若干架航空器对各筛选方法的时间消耗的影响。实验条件同前,只是每次增加的航空器个数由1个逐步增加到25个。在每种情况下进行100次蒙特卡罗实验,统计结果如图6所示。与图4相比较可见,距离门限法和SDT方法的时间消耗一致,而对于改进的DDT方法,时间消耗存在一定的增长。这是因此每次增加的航空器数目不同,局部更新的量也相应地增大,从而导致时间消耗增加。

图6　批量增加空域内航空器数量对刷新时间的影响

最后,分析空域Delaunay剖分中存在反转三角形时,各种筛选方法的时间消耗。考虑空域内存在航空器200架,通过交换某个三角形的两个顶点坐标来形成反转三角形,分别统计存在1个到25个反转三角形时的几种方法的时间消耗。在每个实验条件下进行100次蒙特卡罗实验,实验结果如图7所示。由图7可见,当空域内Delaunay剖分中存在反转三角形时,空域内航空器数目未发生改变,所以不影响距离门限方法和SDT方法的时间消耗,而对于改进的DDT方法,反转三角形数量影响着局部更新复杂度,随着反转三角形数量的增大,改进的DDT方法的时间消耗呈线性增长。在实际运行环境中,瞬时增加的反转三角形的个数通常较少,一般不会超过3个,由图7可见,在较少反转三角形的条件下,改进的DDT方法的时间消耗明显低于其他方法。

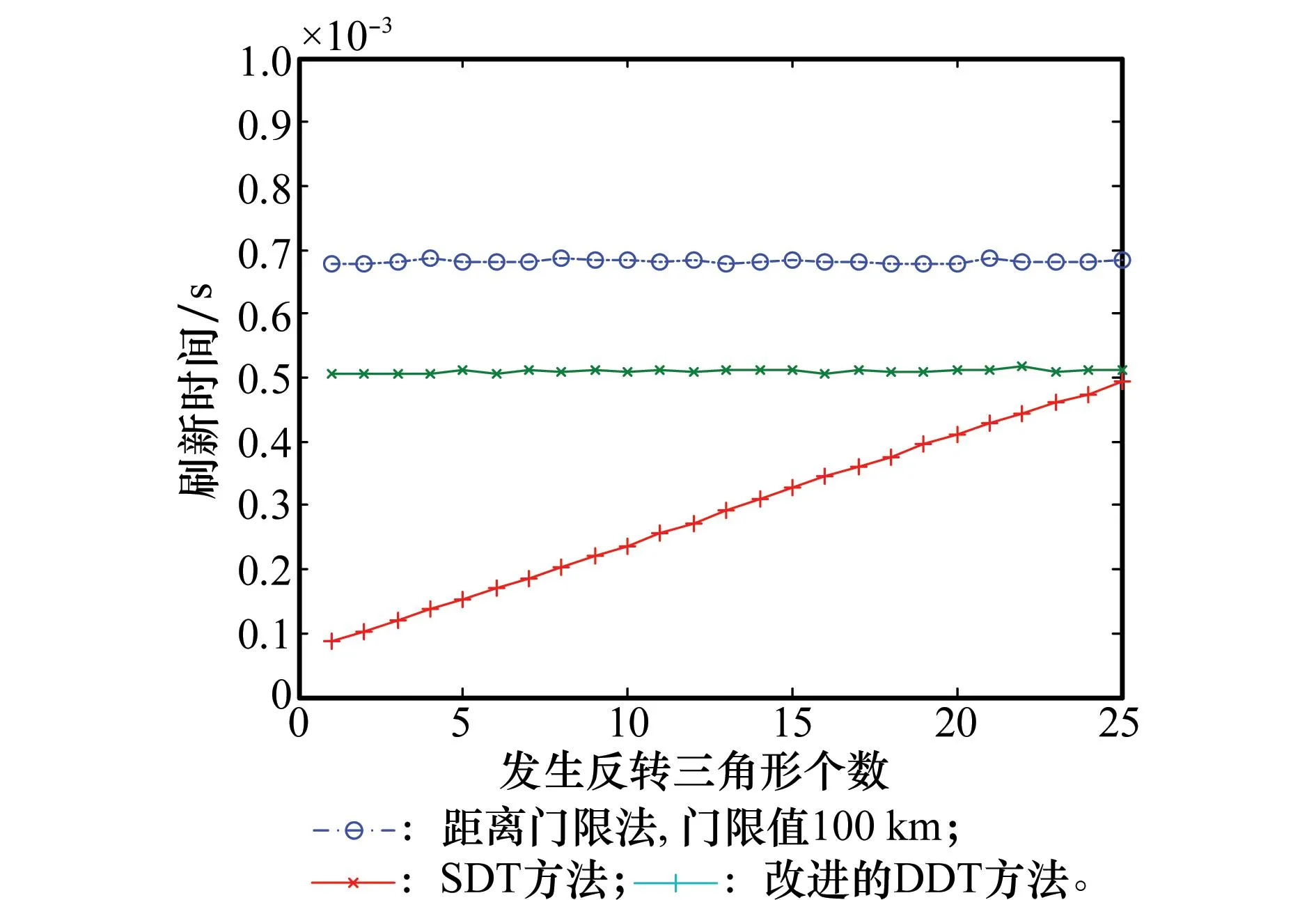
图7　空域内反转三角形个数对刷新时间的影响

5结论

本文对DDT方法的改进,使其可以有效地解决空域Delaunay三角剖分中的反转三角形检测问题,通过对反转点的确定,可以用顺序点删除与点添加的局部更新方式实现对反转三角形的局部更新。本文所提方法既保持了DDT方法的局部更新特点,又解决文献[9]中DDT方法无法对反转三角形情况进行拓扑更新的缺陷,因此,本文提出的改进的DDT方法是一种稳健、高效的Delaunay三角剖分动态维护方法。实验结果表明,该方法在航空器潜在冲突筛选处理上具有较明显的效率优势。

参考文献：

[1] EUROCONTROL. Eurocontral guidance material for short term conflict alert, May 2009[EB/OL].[2015-06-13].http:∥www.eurocontrol.int/publications/eurocontrol-guidance-material-short-term-conflict-alert.

[2] Hess M, Heidger R, Bredemeyer J. Tracker quality monitoring by nondedicated calibration flights[J].IEEEAerospaceandElectronicSystemsMagazine, 2014, 29(8): 10-16.

[3] Liu W, Hwang I. Probabilistic aircraft mid-air conflict resolution using stochastic optimal control[J].IEEETrans.onIntelligentTransportationSystems, 2014, 15(1): 37-46.

[4] Matsuno Y, Tsuchiya T. Stochastic 4D trajectory optimization for aircraft conflict resolution[C]∥Proc.oftheIEEEAerospaceConference, 2014：1-10.

[5] Richard E, Jonathan F. Multiobjective optimization of safety related systems: an application to short-term conflict alert[J].IEEETrans.onEvolutionaryComputation, 2006, 10(2): 187-198.

[6] Chiang Y J, Klosowski J T, Lee C, et al. Geometric algorithms for conflict detection/resolution in air traffic management[C]∥Proc.ofthe36thIEEEConferenceonDecisionandControl, 1997: 1835-1840.

[7] Liu X, Han S C. Delaunay method for free flight conflict detection[J].JournalofDataAcquisition&Processing,2002,17(4):446-449.(刘星,韩松臣.用于自由飞行冲突探测的Delaunay方法[J].数据采集与处理,2002,17(4):446-449.)

[9] Su Z G, Wang Z, Wu R. Robust dynamic Delaunay triangulation technology for moving points[J].SystemsEngineeringandElectronics, 2013, 35(8): 1764-1768. (苏志刚, 王争, 吴仁彪. 面向移动点的稳健动态Delaunay三角剖分技术[J].系统工程与电子技术, 2013, 35(8): 1764-1768.)

[10] Rubin N. On kinetic Delaunay triangulations: a near quadratic bound for unit speed motions[C]∥Proc.oftheIEEE54thAnnualSymposiumonFoundationsofComputerScience, 2013, 519-528.

[11] Zhou Y, Sun F, Wang W, et al. Fast updating of Delaunay triangulation of moving points by bi-cell filtering[J].ComputerGraphicsForums, 2010, 29(7): 2233-2242.

[12] Machado P, Castro M, Tournois J, et al. Filtering relocations on a Delaunay triangulation[J].ComputerGraphicsForums, 2009, 28(5): 1465-1474.

[13] Zhou Y F, Sun F, Wang W P, et al. A new algorithm for fast updating Delaunay triangulation of moving points based on local fixing[J].JournalofComputer-AidedDesign&ComputerGraphics,2011,23(12):2006-2012.(周元峰,孙峰,王文平,等. 基于局部修复的移动数据点Delaunay三角化快速更新方法[J].计算机辅助设计与图形学学报,2011,23(12):2006-2012.)

[14] Kolingerová I, Žalik B. Improvements to randomized incremental Delaunay insertion[J].ComputersandGraphics, 2002, 26(3): 477-490.

[15] Guibas L, Russel D. An empirical comparison of techniques for updating Delaunay triangulations[C]∥Proc.ofthe20thAnnualSymposiumonComputationalGeometry, 2004：170-179.

[16] Devillers O. On deletion in Delaunay triangulation[C]∥Proc.ofthe15thAnnualACMSymposiumonComputationalGeometry, 1999: 181-188.

[17] Rubin N. On topological changes in the Delaunay triangulation of moving points[J].Discrete&ComputationalGeometry, 2013, 49(4) : 710-746.

苏志刚(1972-),男,教授,博士,主要研究方向为雷达信号处理、阵列信号处理、空中交通管理、信息融合。

E-mail:ssrsu@vip.sina.com

符笑娴(1990-),女,硕士研究生,主要研究方向为空中交通管理、冲突检测。

E-mail:fuxiaoxian1990@163.com

郝敬堂(1989-),男,助理实验员,硕士,主要研究方向为空中交通管理、空管目标仿真、空管中间件。

E-mail:liuzhijingquan1989@126.com

Dynamic triangulation based method for screening potential conflicts

SU Zhi-gang1,2, FU Xiao-xian1,3, HAO Jing-tang1

(1.Sino-EuropeanInstituteofAviationEngineering,CivilAviationUniversityofChina,Tianjin300300,China;2.TianjinKeyLaboratoryforAdvancedSignalProcessing,CivilAviationUniversityofChina,Tianjin300300,China; 3.FujianGeneralAviationIndustryCompanyLimited,Fuzhou350000,China)

Abstract:Focusing on the difficulty that the dynamic delaunay triangulation (DDT) method could not stably realize local updating for the inverted triangle produced in the airspace triangulation, a modified method is proposed to replace the local updating for the inverted triangle with two local updatings in sequence in cases of point deletion and point insertion. Experimental results show that the number of potential conflict aircrafts using the modified DDT is independent with the aircraft density in airspace, and the modified DDT method has much lower time complexity of local updating. Modified DDT is more robust and more suitable for screening the potential conflict aircrafts in the air traffic control automation system.

Keywords:air traffic management; conflict detection; dynamic delaunay triangulation (DDT); moving point set; dynamic updating

收稿日期：2015-02-15；修回日期：2015-12-16；网络优先出版日期：2016-03-22。

基金项目：国家科技支撑计划 (2011BAH24B12)；中央高校基本科技业务费中国民航大学专项项目(3122014H003)资助课题

中图分类号：TP 302

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.36

作者简介：

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160322.1650.010.html