Phased-MIMO雷达恒模正交波形优化设计

陈志坤, 冯　翔, 李风从, 乔晓林, 赵宜楠

(1. 哈尔滨工业大学电子与信息工程学院， 黑龙江 哈尔滨 150001；2. 南方科技大学电子与电气工程学院， 广东 深圳 518000)



Phased-MIMO雷达恒模正交波形优化设计

陈志坤1, 冯翔1, 李风从2, 乔晓林1, 赵宜楠1

(1. 哈尔滨工业大学电子与信息工程学院， 黑龙江 哈尔滨 150001；2. 南方科技大学电子与电气工程学院， 广东 深圳 518000)

摘要：由于受到发射机功率和波形能量的限制,现代雷达系统一般选择恒模波形来实现发射功率的最大化利用。针对Phased-MIMO雷达子阵单元之间的恒模正交波形优化设计问题,基于矩阵谱逼近的思想,本文提出了一种新的波形设计框架。首先假设输出信干比的需求得到划分的子阵数目,根据最大信噪比准则对子阵单元进行波束形成,提高了雷达系统的抗干扰性能,其次采用迭代矩阵谱逼近算法(iterative matrix spectral approximation algorithm, IMSAA)对子阵单元之间的正交波形进行优化设计,相对于multi-CAN算法,该算法能够获得更好的相关性能,而且运算效率较高,最终实现了恒模波形的优化设计。仿真结果证明了算法的有效性。

关键词：Phased-MIMO雷达; 波形设计; 正交波形; 恒模波形

0引言

与传统的相控阵雷达相比,集中式多输入多输出(multiple input multiple output,MIMO)雷达具有更高的分辨率和参数估计精度,更多的识别目标数,更强的抗截获能力,因此成为了新体制雷达领域的研究热点[1-3]。理论上,集中式MIMO雷达需要长时间相干积累来弥补由波形分集所导致的信噪比损失。然而在实际应用中,由于载机平台和目标的运动使得长时间相干积累较为困难[4-5]。因此,如何提高输出信噪比是集中式MIMO雷达工程化一个至关重要的前提条件。文献[6]将MIMO雷达和相控阵雷达两种体制叠加设计,对阵列几何进行子阵划分,子阵单元是相控阵体制,而子阵单元之间则是MIMO雷达的体制,并称之为相控阵-MIMO混合体制(hybrid MIMO phased-array)雷达。该混合体制雷达综合了两种雷达体制,同样也分为于集中式和分布式两种方式,二者的后续处理是完全不同的,如分布式主要利用空间分集提高对微弱信号的检测能力,如文献[8]提出了一种新的MIMO雷达体制-MSRS[7],有效改善了低信噪比情况下的检测性能,集中式主要侧重于发射波形的优化设计,以上两种混合体制雷达都以牺牲硬件成本和系统的复杂性实现输出信噪比增益的改善。文献[8]提出了Phased-MIMO雷达的概念。该雷达属于集中式MIMO雷达,与混合体制的MIMO雷达不同的是,它采用了重叠子阵的划分方式来获取更大的相干增益,并能够对发射子阵的方向图进行灵活设计。由此可见,Phased-MIMO雷达综合了MIMO雷达和相控阵雷达各自的优点形成了一种新的雷达体制,是集中式MIMO雷达一个新的分支技术,吸引了学者的广泛关注,并被视为未来相控阵雷达的发展模式[9]。文献[10]对Phased-MIMO重叠子阵的划分进行研究。文献[11]通过对Phased-MIMO雷达的模糊函数进行推导,证明了其能够有效地改善了分辨率性能。由于重叠子阵的特殊性,Phased-MIMO雷达一般采用线性调频信号[8]。以上的研究工作,只是证明了线性调频信号能够满足正交条件,并未涉及到实际发射波形的设计,而且重叠子阵的划分是一个有待于研究的关键问题[12]。然而理想的正交波形并不存在,与空间正交信号类似,频率正交信号可使用优化算法对其相关性能进行优化,需要具有较高的自相关峰。此外,为了最大化利用发射机功率和避免放大器非线性特性导致的波形畸变,现代雷达的波形设计需要满足恒模的约束[13]。

针对以上分析,本文首先需要确定重叠子阵的划分数目以及子阵单元的权值向量,其次为了提高Phased-MIMO雷达频率正交信号的相关性能,需要对其优化问题进行建模,并将优化算法引入优化模型中对目标函数进行求解,以此实现了恒模正交波形的优化设计。

1问题建模

假设单基地MIMO雷达系统由N个天线组成,s(t)[s1(t),s2(t),…,sN(t)]T,满足正交波形的条件。

(1)

Phased-MIMO雷达的建模思想就是将MIMO雷达的阵列分成K个可重叠的子阵(1≤K≤N),每个子阵由小于N的任意阵元数所组成。Phased-MIMO雷达的阵列几何如图1所示。

图1　相控-MIMO雷达的阵列几何

(2)

式中,φk(t)为第k个子阵的发射信号；Q为脉冲幅度；T0为脉冲间隔时间；多普勒频移Δf=fk+1-fk,且Δf≫1/T0,为前一个阵元和后一个阵元的频率差,同时也是前一个子阵和后一个子阵的频率差,由文献[14]可证明

(3)

式中，k,k′∈K。

(4)

由式(4)可见,通过对τ和Δf的设计可保持子阵单元之间的发射信号正交。τ是阵元间距所决定的,本文已设定阵元间距为半个波长,因此针对Δf的设计可得到自相关性能良好的线性调频波形,以此实现子阵单元之间的MIMO雷达体制。自相关的峰值旁瓣水平是衡量信号的正交性能一个重要指标。

(5)

(6)

式中,β(θ)为反射系数,则有

(7)

为相干处理发射矢量,且c(θ)∈CK×1,wk为波形形成的权值向量,则波形分集矢量d(θ)∈CK×1为

(8)

(9)

式中,u(θ)(c(θ)⊙d(θ))⊗b(θ),u(θ)∈CKN×1,表示在方位θ的联合导向量；表示KN×1的噪声项。则雷达系统的输出信干噪比可定义为

SINRPhase-MIMO=

(10)

为了进一步提高Phased-MIMO雷达的输出信干噪比增益,根据自适应波束形成的原理,本文将对Phased-MIMO雷达相控阵模式子阵单元进行波束形成。

2相控-MIMO雷达恒模波形优化

由式(5)可知,Phased-MIMO雷达的波形优化需要满足两种设计目标:其一是相控子阵的波束形成,关系到雷达系统输出的信干噪比性能,文献[8]针对MVDR波束形成算法进行优化,本文针对干扰信号采用最大信噪比准则进行改进和推导;其二则是恒模正交波形的优化设计,文献[8]只是证明式(3)能满足正交的条件,并未对真实信号进行实现。因此,本文将对线性调频信号的频率正交性进行问题建模,将其转化为波形序列的自相关和互相关优化问题。最后,在交替投影的算法框架中对恒模波形进行实现。为了表述算法,定义投影算子为

(11)

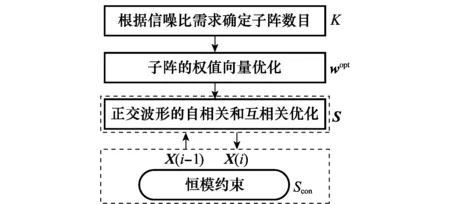
图2　面向波束形成相控-MIMO雷达的波形设计框架

2.1基于最大信噪比准则的波束形成

由图2所示,第一级优化将根据最大信噪比准则(Max-SNR)对子阵单元进行波束形成,由此获取最优的权值向量[15]：

(12)

(13)

可得到

(14)

2.2恒模正交波形优化设计

由式(2)可得,本文所设计的波形为线性调频波形。假设每个阵元使用一个码长为L的波形,则构成一个波形矩阵S∈CL×N,S=[s1,s2,…,sK]。本文基于矩阵谱逼近和相位提取的思想[14-15],以及相关与谱之间的关系,通过迭代的方式对对恒模正交波形进行优化设计实现,可转化为波形的自相关和互相关的优化问题,定义序列间的非周期相关函数为

(15)

式中，Uk∈RL×L为移位矩阵,定义如下：

(16)

当k=k′时,表示波形的自相关函数,本文使用al(sk)∈CL×N表示cl(sk,sk)。因此波形设计的目的就是减少所设计的波形与理想波形的误差,假设理想波形之间的互相关均为0,由此可得代价函数

(17)

式中,Diag(·)表示对角加载；|S|=1表示各个元素的模值全为1。基于以上,式(17)可转换为矩阵谱逼近非周期相关的优化问题。

(18)

(19)

(20)

其中,tr(·)表示矩阵的迹;1表示全1的矩阵，且将式(20)命名为迭代矩阵谱逼近算法(iterative matrix spectral approximation algorithm,IMSAA)。与Multi-CAN算法的循环迭代方式相比,该算法利用子空间的特征值分解并以矩阵谱逼近的方式直接对自相关的性能进行优化,能够最大程度改善了自相关性能,然而却牺牲了小部分的互相关性能,同时在迭代过程中简化了多维矩阵的运算,由此提高了算法的效率性。

为了约束包络的幅度,实现恒模波形的设计[16],定义集值函数为

(21)

式中，M(1)代表模值为全1的恒模约束集合,令S=M(1),最终可得到恒模波形约束的投影算子为

proj(X,S)=exp(j∠X)

(22)

式中,∠表示相位取角,由此在交替投影的算法框架下可求得正交恒模波形矩阵X。

由以上的分析,可得到以下的波形设计步骤:

步骤 1选择信噪比增益,由式(24)求得子阵的阵元数目K;

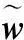
步骤 3计算:由式(5),得到发射信号矩阵S;

3仿真结果分析

为了验证本文提出Phased-MIMO雷达波形设计的性能,设置仿真条件:阵元数N=10,为均匀线性阵列(uniformlinearray,ULA),阵元间距d=λ/2,功率约束波形采样数L=256,功率约束c=N/K。

仿真 1根据信噪比增益求得Phased-MIMO的方向图,分别与相控阵雷达、MIMO雷达进行对比。

(1) 当只有噪声环境下,设噪声功率σn为1,输入信噪比为-20～0dB。由式(10)可得

(23)

首先本文选择需求的输出信噪比增益SINRd=SINRPhase-MIMO≥25dB,由式(10)可求得K为

(24)

计算可得并取整K=5,并得到以下仿真结果,如图3所示。

图3　只有噪声情况下3种雷达的输出信噪比

当只有噪声的情况下单个阵元的输入信噪比为0dB时,MIMO雷达(K=10)的输出信噪比为20dB,相控阵雷达(K=1)的输出信噪比增益为30dB,而Phased-MIMO雷达(K=5)的输出信噪比则为26dB。因此相对于MIMO雷达,Phased-MIMO雷达获得了6dB以上的输出信噪比增益。

由图4可见,传统MIMO雷达在空域不形成发射方向图,与相控阵雷达相比,由于阵元数的减少,Phased-MIMO雷达方向图的旁瓣水平比相控阵雷达稍高,主瓣宽度较宽。

图4　3种雷达的发射方向图

(2) 当干扰与噪声同时存在时,设信干噪比为σs/σn+σi,当干扰信号的功率远大于噪声功率时,式(9)的噪声项可以忽略,假设干扰的功率为50 dB,噪声功率为1,输入信噪比为-20～0 dB,可得以下仿真结果。

由图5可得,当输入信噪比为-20～0 dB时,MIMO雷达与相控阵雷达的输出信噪比几乎重合,而Phased-MIMO雷达(K=5)能够获得5.56 dB的输出信噪比增益。

图5　3种雷达的发射方向图

仿真 2假设干扰和高斯白噪声同时存在的环境下,子阵划分数K=5,信号与噪声平均功率均为0 dB,而干扰信号的平均功率为50 dB。感兴趣目标方位在0°,干扰信号位于20°,基于以上先验信号,根据最大信噪比准则对相控子阵进行波束形成,由此获取最优的权向量wopt。

如图6所示,在干扰和高斯噪声环境中,发射方向图已经变成干扰的方向图。由图7所示,根据最大信噪比准则对权值向量进行优化,子阵的方向图能够取得了约9 dB的旁瓣深度。

仿真 3为了实现子阵单元之间的MIMO雷达体制,以频率正交信号作为重叠子阵单元之间的发射信号,提出IMSAA算法对频率正交信号进行优化设计,得到相关性能良好的恒模正交波形,并与国际通用的Multi-CAN算法进行对比,验证了算法的有效性。设重叠子阵划分的数目K=5Δf的初始值为归一化频率区间[0～1]的随机数, 码长L=256,算法进行100次蒙特卡罗仿真实验,以最低的自相关和互相关峰值作为仿真结果进行对比。为了方便比较,定义归一化相关幅值为

(25)

图6　发射信号+干扰信号+噪声的功率谱

以下只列举了当k1=1的自相关及与k2=2的互相关,其他仿真结果由表1和表2表述。

表1　基于Multi-CAN算法波形序列的自相关峰值和

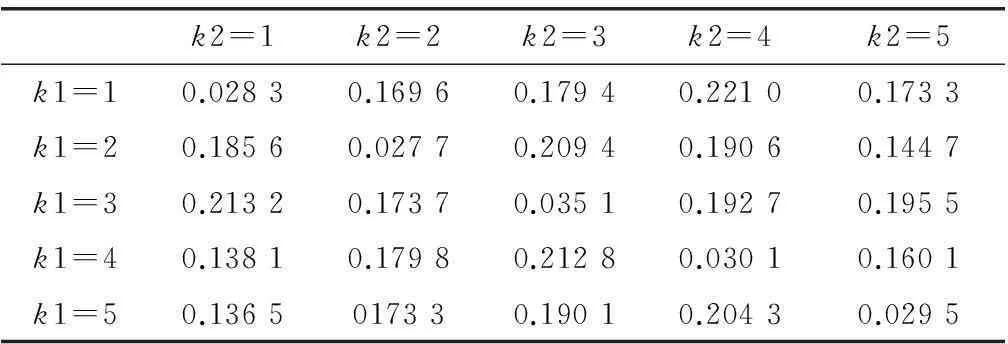
表2　基于IMSAA算法波形序列的自相关值和互相关峰值旁瓣值

注: 1) 当k1=k2=k时,表示第k个子阵的发射波形自相关峰值旁瓣值;2) 当k1≠k2时,表示第k1个子阵与第k2子阵的发射波形互相关峰值旁瓣值。ASPs ,CPs分别表示所有波形序列的自相关值和互相关值。

图8表示当k1=1时,第1子阵单元的发射波形自相关图。由图可见,IMSAA算法设计的发射信号X的自相关峰值旁瓣明显低于Multi-CAN。在图9表示当k1=1,k2=2时,第1子阵单元与第2子阵单元的发射波形互相关旁瓣峰值。相对于Multi-CAN,IMSAA算法得到发射波形的自相关峰值旁瓣值较低,而互相关的峰值旁瓣值与Multi-CAN几乎持平。表1与表2表示全部5个子阵单元的发射波形自相关和互相关的峰值旁瓣值。为了定量分析,根据文献[16],定义自相关峰值旁瓣水平为

图7　最大信噪比的方向图

ASP=20lgmax|al(sk)/L|

(26)

和互相关峰值旁瓣水平如下:

CP=20lgmax|cl(sk1,sk2)/L|(dB)

(27)

图8　正交波形的自相关

图9　正交波形的互相关

由表1和表2可见,IMSAA算法自相关峰值旁瓣值低于Multi-CAN,但部分互相关的峰值旁瓣值稍高于Multi-CAN。为了相关性能的进一步比较,在不同的波形序列长度下,对IMSAA算法和Multi-CAN所取得自相关和互相关峰值旁瓣值进行对比。由图10可得,相对于Multi-CAN算法, IMSAA算法能够获得8dB左右的自相关旁瓣增益,但由图11可见,该算法牺牲了小部分的互相关旁瓣水平。综合比较两者可得,使用IMSAA算法能够得到相关性能良好的恒模正交信号波形,从而实现了子阵单元之间的正交波形优化设计。另外,由表3可证明IMSAA算法的运行时间优于Multi-CAN。

图10　自相关峰值旁瓣

图11　互相关峰值旁瓣

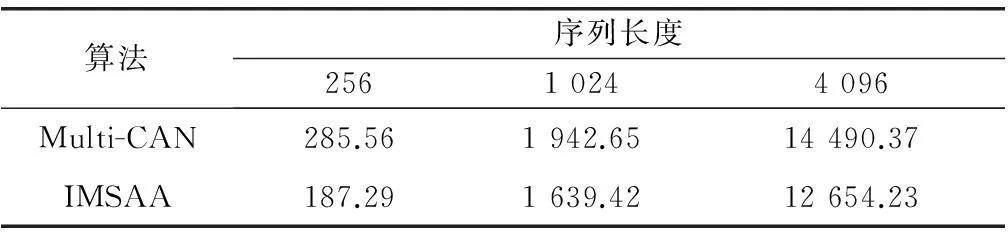
算法序列长度25610244096Multi-CAN285.561942.6514490.37IMSAA187.291639.4212654.23

4结论

本文提出了一种Phased-MIMO雷达恒模正交波形的设计框架,首先根据输出信噪比的增益需求与子阵数目的关系,确定重叠阵列的划分方式,根据最大信噪比准则对子阵单元进行波束形成,由此得到最优权值向量,改善了雷达系统的抗干扰性能,其次比较IMSAA算法和Multi-CAN算法的优化性能,验证了IMASAA算法的有效性,最后,基于相位提取思想对发射信号进行恒模约束实现。但由于阵列的重叠使用,正交波形的优化算法是一个有待于继续改善的问题,比如考虑采用离散频率编码波形的设计。

参考文献：

[1] Li J, Stoica P. MIMO radar with colocated antennas[J].IEEESignalProcessingMagazine, 2007, 24(5): 106-114.

[2] Stoica P, Li J, Yao X． On probing signal design for MIMO radar[J].IEEETrans.onSignalProcessing, 2007, 55(8): 4551-4561.

[3] Li J, Stoica P, Xu L Z, et al. On parameter identifiability of MIMO radar[J].IEEESignalProcessingLetters,2007,14(12):968-971.

[4] Daum F, Huang J. MIMO radar: snake oil or good idea?[J].IEEEAerospaceandElectronicSystemsMagazine, 2009, 24(5): 8-12.

[5] Aboulnasr H, Sergiy A V. Transmit/receive beamforming for MIMO radar with collocated antennas[C]∥Proc.oftheIEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing, 2009: 2089-2092.

[6] Daniel R F. Signaling strategies for the hybrid MIMO phased-array radar[J].IEEETrans.onSignalProcessing, 2010, 4(1): 66-78.

[7] Xu J, Dai X Z, Xia X G, et al. Optimizations of multisite radar system with MIMO radars for target detection[J].IEEEAerospaceandElectronicSystems, 2011, 47(4): 2329-2343.

[8] Aboulnasr H, Sergiy A V. Phased-MIMO radar:a tradeoff between phased-array and MIMO radars[J].IEEETrans.onSignalProcessing, 2010, 58(6), 3137-3151.

[9] Aboulnasr H. Why the phased-MIMO radar outperforms the phased-array and MIMO radar[C]∥Proc.ofthe18thEuropeanSignalProcessingConference, 2010: 1234-1238.

[10] Ismail N E, Mahmoud S H. A new phased MIMO radar partitioning schemes[C]∥Proc.oftheIEEEonAerospaceConferenceWorkShop, 2014: 1-7.

[11] Waseem K. Ambiguity function of phased-MIMO radar with colocated antennas and its properties[J].IEEETrans.onSignalProcessingLetter, 2014, 11(7): 1220-1224.

[12] Sajid A, Mohamed S. MIMO-radar waveform covariance matrix for high SINR and low side-lobe levels[J].IEEETrans.onSignalProcessing, 2014, 62(8): 2056-2065.

[13] He H, Stoica P, Li J. Designing unimodular sequences sets with good correlations-including and application to MIMO radar[J].IEEETrans.onSignalProcessing, 2009, 57(11): 4391-4405.

[14] He Q, Blum R, Godrich H, et al. Target velocity estimation and antenna placement for MIMO radar with widely separated antennas[J].IEEEJournalofSelectedTopicsSignalProcessing, 2010,4(1):79-100.

[15] Liu Y F, Liu Z, Liu J. MIMO radar waveform design based on high-resolution range profile[J].SystemsEngineeringandElectronics, 2011, 33(4): 755-758.(刘韵佛, 刘峥, 刘俊. 基于高分辨距离像的MIMO雷达波形设计[J]. 系统工程与电子技术, 2011, 33(4): 755-758.)

[16] Zhao Y N, Li F C, Zhang T. Computational design of optimal waveforms for MIMO radar via multi-dimensional iterative spectral approximation[J].MultidimensionalSystems&SignalProces-sing,2014,46(22):1-18.

陈志坤(1982-),男,工程师,博士研究生,主要研究方向为雷达信号处理、电子侦察技术。

E-mail：chih_quinn_chen@yeah.net

冯翔(1988-),男,博士研究生,主要研究方向为认知雷达。

E-mail：fengxiang230316@163.com

李风从(1985-),男,博士后,主要研究方向为通信与信息系统。

E-mail：xialulee@sina.com

乔晓林(1948-),通信作者,男,教授,博士,主要研究方向为雷达系统、电子对抗。

E-mail：paulxiao@sohu.com

赵宜楠(1977-),男,教授,博士,主要研究方向为雷达信号处理、自适应波束形成。

E-mail:hrbzyn@163.com

Constant orthogonal waveform optimal design for Phased-MIMO radar

CHEN Zhi-kun1, FENG Xiang1, LI Feng-cong2, QIAO Xiao-lin1, ZHAO Yi-nan1

(1.SchoolofElectronicsandInformationEngineering,HarbinInstituteofTechnology,Harbin150001,China; 2.DepartmentofElectronical&ElectronicEngineering,SouthUniversityofScienceandTechnologyofChina,Shenzhen518000,China)

Abstract:By the limit of transmitter power and waveform energy, modern radar generally chooses constant modulus waveform to achieve the goal that maximum use of transmission power. We address the optimization problem of constant modular orthogonal waveform design for Phased-multiple input multiple output (MIMO) radar, and a new waveform optimal design framework for Phase-MIMO radar based on the matrix spectral approximation is presented. First, the number of sub-array can be obtained by the requirements of signal to noise ratio (SNR), the beam of subarray is patterned according to the maximum SNR criterion, effectively improving the anti-jamming performance of the radar system. Then, the orthogonal waveform among subarray units is optimized via the iterative matrix spectral approximation algorithm (IMSAA), which has a better correlation performance and is more computationally efficient than multi-CAN. Finally, the constant modulus signal is optimally designed. Simulation results demonstrate the effectiveness of the proposed algorithm.

Keywords:phased-multiple input multiple output (MIMO) radar; waveform design; orthogonal waveform; constant modulus waveform

收稿日期：2015-05-22；修回日期：2016-02-18；网络优先出版日期：2016-04-29。

基金项目：国家自然科学基金(61371181)资助课题

中图分类号：TN 957.51

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.11

作者简介：

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160429.1001.002.html