零陷可控的低旁瓣频率不变宽带波束形成

张书瑞, 马晓峰, 盛卫星, 韩玉兵, 张仁李

(南京理工大学电子工程与光电技术学院, 江苏 南京 210094)



零陷可控的低旁瓣频率不变宽带波束形成

张书瑞, 马晓峰, 盛卫星, 韩玉兵, 张仁李

(南京理工大学电子工程与光电技术学院, 江苏 南京 210094)

摘要：在基本的傅里叶变换频率不变波束形成器(frequency invariant beamforming, FIB)的基础上,提出了快速可控零陷低旁瓣宽带FIB优化方法,该方法将固定角度方向图零陷约束和等波纹原型滤波器加入FIB的设计,实现了零陷可控的低旁瓣FIB。同时,还开展了FIB抽头系数的稀疏优化,有效的降低了算法实现的运算量。仿真结果验证了所提的方法在一维均匀线阵和二维均匀面阵上的正确性和有效性。

关键词：频率不变波束形成; 宽带波束形成; 抗干扰零陷; 低旁瓣

0引言

在无线通信、雷达和声呐领域中,自适应宽带数字波束形成[1-5]是非常重要的研究课题,可以有效的抑制干扰信号,增强期望信号。

空时联合优化技术[6-11]常用于宽带自适应阵列信号处理中,这类方法所需的二维自适应系数的维数较大,运算复杂,迭代收敛速度慢。

时域真延时技术[12-15]也是宽带自适应阵列信号处理的主要研究方向。由于所需的最小延时量很小,一般都是采样周期的分数倍延时,需要分数阶延时来实现宽带波束形成。有两大类分数阶真延时方法:光分数延时和数字分数延时。数字分数延时一般通过加窗法、最大平坦准则法或者Farrow结构等来优化横向滤波器延迟抽头系数,实现分数阶延时。光分数延时、数字加窗法和数字最大平坦准则法在不同的延时要求情况下,都要重新设计;数字Farrow时延滤波器采用可变延时的横向滤波结构,延时量控制灵活,但其实现复杂度高。并且采用真延时进行波束形成,方向图波束宽度和零极点分布等均随频率变化而变化,无法形成干扰方向具有固定零点的宽带零陷方向图。

频率不变波束形成器(frequency invariant beamforming, FIB)的方向图能够解决宽带波束形成频率不一致的问题,所以近年来,FIB是宽带波束形成一个重要的研究热点。文献[16-18]提出了一维均匀线阵傅里叶变换FIB,该结构与空时联合优化技术所采用的抽头延时结构相同,抽头系数的求解只需要简单的离散傅里叶逆变换(inverse discrete Fourier transform,IDFT)和加窗处理即可。该方法实现简单,并且能够推广到多维阵列[16,18-19]。由于宽带波束形成在高分辨率的要求下,需要大量的阵元和抽头延时线,文献[20]提出了基于子带分解的FIB,该方法将通带范围内的信号分解为相应子带进行窄带波束形成,然后利用最小二乘法实现FIB,该方法由于要进行信号子带分解,引入了较大的计算量,提高了算法的计算复杂度。文献[21]利用最小二乘(least squares, LS)准则设计FIB结构,并且进一步提出了在线性约束准则(constrained least squares, CLS)、无约束准则(unconstrained least squares, ULS)和约束整体准则(constrained total least squares, CTLS)下的FIB实现方法。不同约束准则下的优化目标都是最小化不同频点方向图与参考频点方向图的均方误差,算法优化目标直接,但得到的方向图性能与选取的参考方向图有很大关系,且权重计算复杂度较高,方向图的频域一致性也较差。

上述FIB均无法实现低旁瓣控制和抗干扰零陷生成,本文在傅里叶变换FIB[16-19]的基础上,将固定角度方向零陷约束和低旁瓣等波纹原型滤波器引入一维均匀线阵和二维均匀面阵FIB设计中,优化得到了具有频率不变特性的低旁瓣零陷可控宽带波束形成的方向图,并且加入时域抽头延时稀疏优化,有效的减少了横向滤波器的抽头系数,降低了实现复杂度。仿真结果也验证了本文方法的正确性和有效性。

1FIB系统模型

1.1一维均匀线阵的FIB

一维均匀线阵如图1所示。

图1　一维均匀线阵

如图2所示,设S(n,t)为第n个阵元,t时刻接收到的信号:

(1)

式中,c为光速;f为信号频率;θ为来波信号方向。设fs为采样频率(采样周期Ts=1/fs),那么式(1)改写为

(2)

如图2所示,一维均匀线阵宽带FIB的方向图H(f,θ)为

(3)

式中,a(n,k),(n=1,2,…,N;k=1,2,…,K)为一维均匀线阵FIB的系数。参考文献[16-18],定义F1=f/fs, F2=dfsinθ/c,则式(3)可以改写为

(4)

由式(4)可知, 方向图函数G(F1,F2)与a(n,k),满足二维离散傅里叶变换(discreteFouriertransform,DFT)关系,即G(F1,F2)亦为a(n,k)的二维频率响应。

图2　一维线阵FIB的结构

所以只要G(F1,F2)与来波信号频率无关,再通过对G(F1,F2)关于变量F1、F2的IDFT,就能得到FIB的系数a(n,k)。 由F1=f/fs,F2=dfsinθ/c,可知

(5)

要使得宽带波束方向图形状与频率无关,需满足

(6)

一般ΔφI为0,其中I(sinθ)是只与波束指向角度有关的函数。一般地,时域一维低通有限长脉冲响应(finiteimpulseresponse,FIR)滤波器的频响特性与空域波束形成方向图具有对应关系[22], 式(6)中的I可以通过一维原型FIR低通滤波器的频响特性来表征,这样就可以设计出期望的FIB方向图。

当波束指向θ=0°时,相当于一维原型低通FIR滤波器频响特性的归一化频率F=0。因为F∈[-0.5,0.5],sinθ∈[-1,1],又要满足F=0时sinθ=0,参考文献[16-18],定义F=sinθ/2。

更一般的,当波束指向θ=θo,一维原型低通FIR滤波器的通带范围就要在频率维上平移sinθo/2,那么F=(sinθ-sinθo)/2。波束指向偏离法线情况与指向法线情况下分析方法相同,为了简化分析,后续仅考虑波束指向法向情况,即F=sinθ/2。

已知X阶一维原型低通FIR滤波器的系数为p(x),一般X为奇数,那么其频响特性P(F)可以表示为

(7)

因此,式(6)中的I(sinθ)可以表示为

(8)

那么一维均匀线阵FIB的系数a(n,k)计算步骤为

步骤 1将式(8)代入式(6)中,得

(9)

步骤 2将式(9)中求得的G(F1,F2)进行二维IDFT,求得q(n1,n2);

步骤 3对q(n1,n2)在 n1和 n2维度上分别用N点和K点的窗函数进行加窗处理,得到一维均匀线阵FIB的系数a(n,k)。

1.2二维均匀面阵的FIB

二维均匀面阵如图3所示。

图3　二维均匀面阵

设面阵的阵元数为M×N,阵元位于xoy平面,阵元间距为d, 各阵元为各向同性的全向天线,每个阵元对应时域抽头滤波器阶数为K,那么标号为(n,m) (n=1,2,…,N,m=1,2,…,M)的阵元接收到的来波信号S′(n,m,k)为

(10)

那么波束方向图H′(f,θ,φ)为

(11)

式中, θ∈[0°,90°]为俯仰角;φ∈[0°,360°]为方位角;a′(n,m,k)(n=1,2,…,N； m=1,2,…,M； k=1,2,…,K),为二维均匀面阵FIB的系数。设U=sinθcosφ(U∈[-1,1]),V=sinθsinφ(V∈[-1,1]),那么式(11)可以改写为U-V空间的形式

(12)

定义F3=dfU/c, F4=dfV/c, F5=f/fs,那么式(12)又可以进一步改写为

(13)

由式(13)可知,G′(F3,F4,F5)为二维均匀面阵的FIB方向图;且G′(F3,F4,F5)与系数a′(n,m,k)满足三维DFT关系,即G′(F3,F4,F5)亦为a′(n,m,k)的三维频率响应。要得到二维均匀面阵的FIB方向图与来波信号频率无关,只与来波信号方向有关即

(14)

(15)

(16)

式中，|U|2+|V|2≤1。

更一般的,若要使二维均匀面阵的波束指向U0、V0,式(16)改写为

(17)

式中,|U-U0|2+|V-V0|2≤1。

波束指向偏离法线情况与指向法线情况下分析方法相同,为了简化分析,后续仅考虑波束指向法向情况,二维原型滤波器的设计用式(16)即可。

那么二维均匀面阵FIB的系数a′(n,m,k),计算步骤如下:

步骤 1已知U=F3c/(F5fsd), V=F4c/(F5fsd),将式(16)代入式(14)得

(18)

2零陷可控的低旁瓣FIB

2.1一维均匀线阵的零陷可控低旁瓣FIB

已知干扰方向为θJ,在FIB的设计中,将一维均匀线阵系数a(n,k)的二维频率响应G(F1,F2)在θJ所在位置及其附近的一定区域的值设置为ΔD(该值与零陷深度有关,一般取0),控制该区域零陷产生,达到抗干扰的目的,具体设置方法如下。

当干扰角度为θJ时,要在θJ附近±Δθ都产生零陷,那么就要使得式(9)在|θ-θJ|≤Δθ时,G(F1,F2)为ΔD,即

(19)

文献[16-18]中的一维FIR原型滤波器为低通滤波器,将低通滤波器替换为切比雪夫加权的等波纹滤波器。设X阶等波纹滤波器系数为p′(x)(x=1,2,…,X),那么式(19)可以表达为

(20)

按照式(20)给出的表达式,再根据第1.1节描述的一维均匀线阵FIB设计步骤,可以实现一维均匀线阵零陷可控低旁瓣的FIB。

为了评价FIB方向图的频域一致性,参考文献[21],给出方向图频域一致性均方误差R的定义

(21)

式(21)中fr为参考信号频率,在FIB的实际应用中,需要保证通带范围内主瓣区的方向图一致性,可以减少天线系统对宽带信号接收的失真影响;而旁瓣区则只需考虑旁瓣电平特性,干扰零陷区只需要考虑零陷深度和宽度即可。因此式(21)的求和范围为主瓣区和通带频率。

2.2二维均匀面阵的零陷可控低旁瓣FIB

已知在U-V空间内,干扰方向为(UJ,VJ),在FIB的设计中,三维幅频响应G′(F3, F4, F5)在UJ和VJ所在位置及其附近的一定区域的值设置为ΔD(一般取0),控制该区域零陷产生,达到抗干扰的目的,即

(22)

式中,Θ为零陷的区域范围。将简单的低通二维滤波器换为二维等波纹滤波器,设Px′(x′)、Py′(y′)分别为X′和Y′阶的等波纹滤波器,X′、Y′一般为奇数,那么式(22)就改写为

(23)

按照式(23)给出的表达式,再根据第1.2节描述的二维均匀面阵FIB设计步骤,就可实现二维均匀面阵的零陷可控低旁瓣FIB。由于二维均匀面阵为一维均匀线阵的推广,二维面阵的方向图频域一致性均方误差与一维线阵的定义类似,这里就不再赘述。

3时域延时抽头稀疏优化

经式(20)约束得到一维均匀线阵零陷可控低旁瓣FIB的系数a(n,k),将其归一化后,设置约束门限Δa,当|a(n,k)|≤Δa时,将a(n,k)设置为0,若高于门限,其值不变,即

(24)

若有一个抽头系数设置为0,抽头延时结构就省掉了一个乘法器和一个加法器。

设抽头系数稀疏后的FIB归一化响应为Hs(f,θ,Δa),与未稀疏的FIB归一化响应误差设置为Bs(f,θ,Δa),即:

(25)

通过设置不同的约束门限Δa,得到相应的的误差Bs(f,θ,Δa)。

二维均匀面阵的时域抽头系数稀疏方法同一维均匀线阵类似,这里就不再赘述。

4仿真结果

4.1一维、二维FIB期望方向图的设计

4.1.1一维原型低通滤波器的设计

仿真条件:一维原型低通FIR滤波器的阶数为23阶,由式(8)得到FIR幅频响应,即期望的一维均匀线阵的FIB方向图如图4所示。

图4　一维均匀线阵期望的归一化方向图

由图4期望的归一化方向图可知,旁瓣电平为13 dB左右,3 dB波束宽度为4.4°。

4.1.2二维原型低通滤波器的设计

仿真条件:二维原型低通滤波器的阶数为11×11,由式(16)得二维原型滤波器的频响特性,即期望的二维均匀面阵的FIB方向图如图5所示。

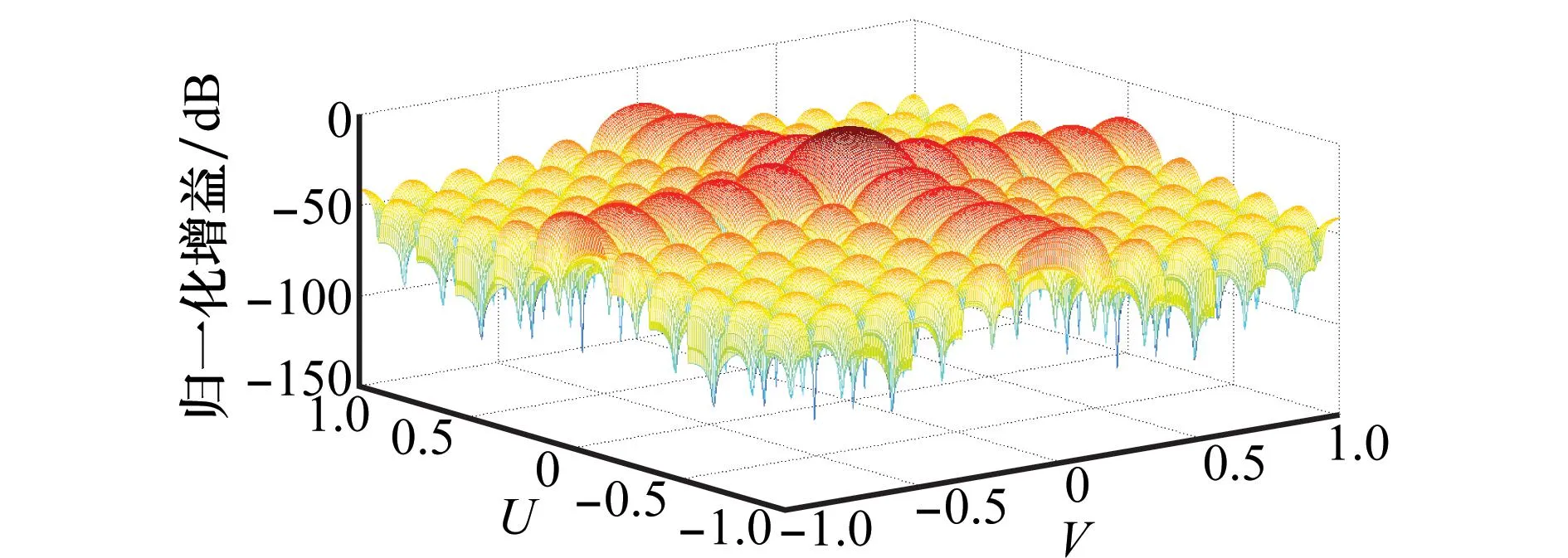
图5　二维均匀面阵期望的归一化方向图

由图5期望的归一化方向图可知,二维均匀面阵期望的方向图的旁瓣电平为13 dB左右。

4.2零陷控制的一维、二维FIB方向图

4.2.1零陷控制的一维FIB方向图

图6的仿真条件:阵元间距为d=cTs,信号的归一化频率范围f/fs∈[0.2,0.45],阵元数N和抽头数K均为61,原型滤波器为第4.1.1节中的23阶低通FIR滤波器,设置式(19)中的θJ=40°,Δθ=4°。

图6　一维均匀线阵不同频率零陷可控FIB归一化方向图

由图6的归一化方向图可以看到,方向图在干扰位置附近(40°±4°)能够产生-40 dB以上的零陷。由于没有进行旁瓣控制,此时旁瓣电平在-13 dB左右,3 dB宽度为4.48°,与图4的期望方向图基本相同。计算方向图频域一致性均方误差R:主瓣区选为[-5°, 5°],归一化的参考频率选为0.45,由式(21)计算得到的归一化方向图的频域一致性均方误差为0.187 6。计算文献[16-18]中的一维线阵FIB频域一致性均方误差为0.173 6。可以看到,添加的零陷控制约束不影响一维均匀线阵方向图的频域一致性。

由图6可知,在频率较低处方向图的零陷控制效果不太显著,这是由于阵元数N和抽头数K与一维原型FIR滤波器的阶数在通带范围内不匹配造成的。若要使得通带范围内都够实现同样的零陷控制效果,有两种方法:①减小一维原型FIR滤波器的阶数;②增加阵元数N和抽头数K。方法①是以降低主瓣增益为代价,方法②是以增加计算复杂度和工程成本为代价。

4.2.2零陷控制的二维FIB方向图

图7的仿真条件:来波信号归一化频率为0.4,阵元数M、N均为61,抽头数K为61,式(22)中的(UJ,VJ)=(-0.010 03,-0.538 5),Θ=0.09,信号的归一化频率为0.4。

图7　频率为0.4时二维均匀面阵零陷可控FIB归一化方向图

图8的仿真条件:来波信号归一化频率为0.3,其他仿真条件与图7相同。

图8　频率为0.3时二维均匀面阵零陷可控FIB归一化方向图

由图7和图8的归一化方向图可以看到,二维均匀面阵的宽带波束方向图在不同频率下的归一化方向图能够保持较好的一致性。旁瓣电平为13 dB左右,在干扰位置UJ为-0.010 03、VJ为-0.538 5附近能够产生-40 dB以上的零陷,由于没有进行旁瓣控制,此时旁瓣电平大概在-13 dB左右。计算二维均匀面阵方向图一致性均方误差R:主瓣区选为|U|2+|V|2≤0.03,归一化的参考频率为0.45,计算得到的零陷控制的二维FIB归一化方向图的频域一致性均方误差为7.692 4;计算文献[16,18-19]中的二维面阵FIB的频域一致性均方误差为7.948 2。可以看到,添加的零陷控制约束不影响二维均匀面阵方向图的频域一致性。

4.3零陷控制的低旁瓣一维、二维FIB方向图

4.3.1零陷控制的低旁瓣一维FIB方向图

图9的仿真条件:将第4.2.1节中的原型滤波器换为23阶等波纹滤波器,等波纹滤波器的旁瓣电平为-35 dB,其他仿真条件同第4.2.1节相同。

图9　一维均匀线阵不同频率零陷可控的低旁瓣FIB归一化方向图

由图9的归一化方向图可以看到,一维零陷可控的低旁瓣FIB的旁瓣降到了-35 dB,3 dB波束宽度展宽为6.04°,所要求的零陷区域仍有-40 dB以上的零陷。由式(21)计算得到的归一化方向图的频域一致性均方误差为0.425 1,能够有效的保证通带期望信号不失真。为了与仿真第4.2.1节对比,原型等波纹滤波器的阶数为23。若要得到更低的旁瓣、更窄的波束宽度,可以适当的增加等波纹原型滤波器的阶数。

下面,将文献[21]提出的基于CTLS准则下的FIB与本文提出的一维均匀线阵低旁瓣零陷可控FIB进行比较。在CTLS准则下,一维均匀线阵的阵元数和抽头数均为61,一维均匀线阵在CTLS准则下的FIB方向图如图10所示。

图10　基于CTLS准则的一维FIB归一化方向图

由图10可以看到,CTLS准则下的FIB整体波束宽带较宽,3 dB波束宽度为7.20;波束一致性较差,计算得到的方向图频域一致性均方误差为0.835 8;该方法没有形成抗干扰零陷,方向图旁瓣电平为-13 dB左右,无法实现低旁瓣控制;在大阵元数和抽头数情况下权重计算复杂度非常高。综上所述,本文提出的零陷可控低旁瓣FIB在性能上优于基于CTLS准则下的FIB。文献[21]中的其他准则也存在上述问题,这里就不再一一列举说明,后续仿真也不再赘述。

4.3.2零陷控制的低旁瓣二维FIB方向图

图11的仿真条件:将第4.2.2节中的二维原型滤波器替换为11×11等波纹二维滤波器,旁瓣电平为-25 dB,其他仿真条件与第4.2.2节相同。由图11的归一化方向图可以看到,二维零陷可控的低旁瓣FIB的旁瓣降到了-25 dB,且所控制的零陷区域仍有-40 dB以上的零陷。计算得到频域一致性均方误差为6.761 5,能够有效的保证期望信号不失真。

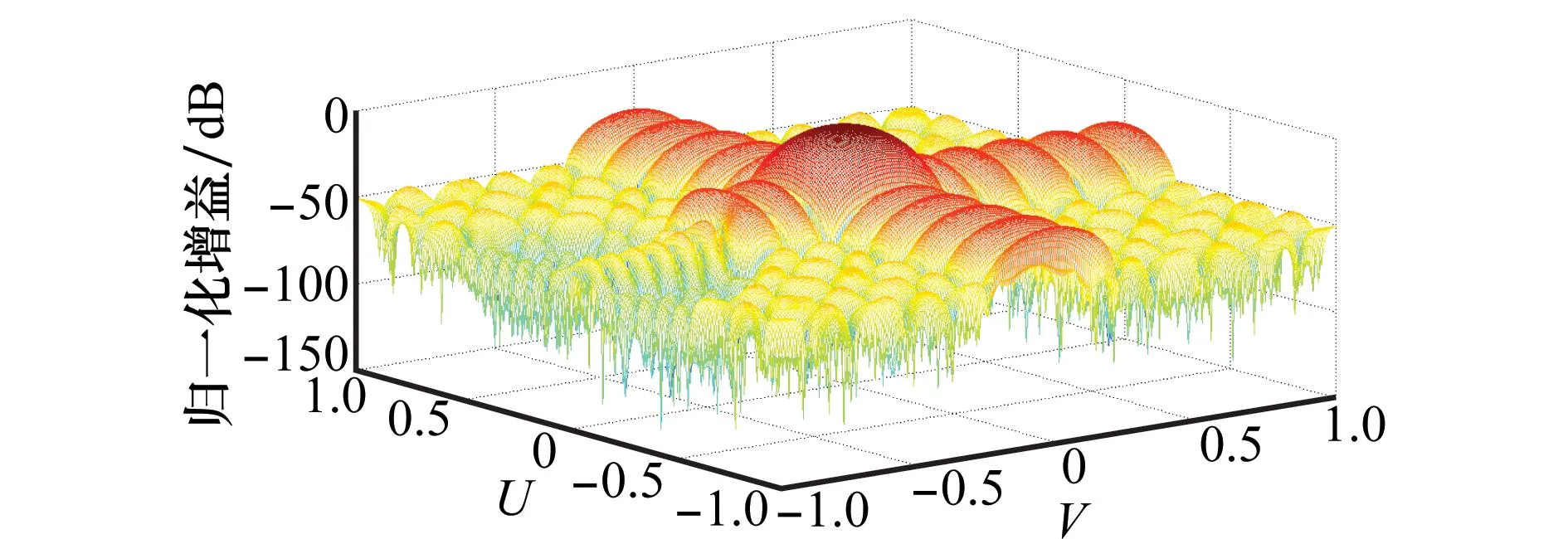
图11　二维均匀面阵零陷可控低旁瓣FIB归一化方向图

4.4稀疏下的零陷控制的低旁瓣一维、二维FIB方向图

4.4.1抽头系数稀疏的零陷控制低旁瓣一维FIB

仿真条件:式(24)中的Δa为9×10-4,其他条件同第4.3.1节中相同,其方向图如图12所示。

经过计算,抽头系数设置为0的个数为1 512个。原有的抽头系数有61×61=3 721个,那么稀疏百分比为1 512/3 721=40%。复杂度降低明显,并且由图9和图12比较可以看得出,系数稀疏后的方向图也能基本保持原有的效果。

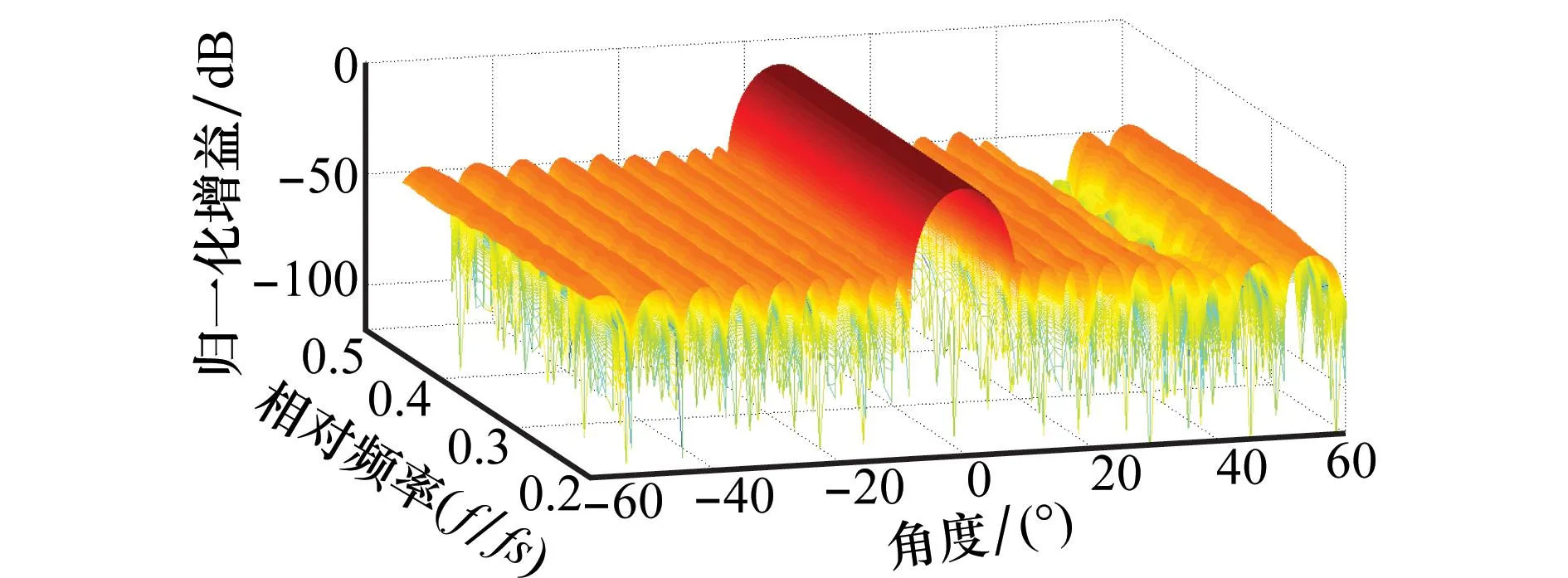
图12　一维均匀线阵不同频率抽头系数稀疏的　零陷可控低旁瓣FIB归一化方向图

表1给出了不同的约束门限Δa,对应的稀疏的抽头个数、方向图误差Bs(f,θ,Δa)、旁瓣电平和频域一致性均方误差,可以看到,稀疏约束门限越高,抽头系数的置零的个数越多,与原方向图的误差越大,最高旁瓣电平越高,频域一致性均方误差越大。

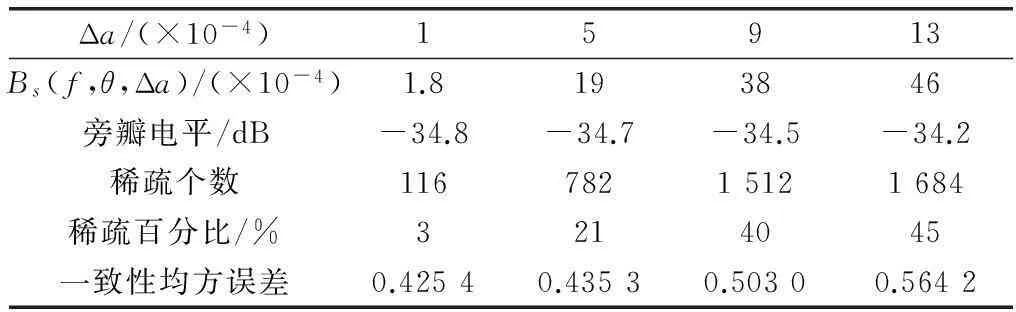
表1　一维FIB稀疏约束门限对方向图性能影响

4.4.2抽头系数稀疏的零陷控制低旁瓣二维FIB

仿真条件:约束门限设置为5×10-3,其他仿真条件与第4.3.2节相同,其方向图如图13所示。

图13　二维均匀面阵阵面抽头系数稀疏的　　　零陷可控低旁瓣FIB归一化方向图

经过计算,省掉的抽头数为120 154个,原有的抽头数为61×61×61=226 981,那么稀疏阵元的百分比为120 154/226 981=52%,复杂度降低明显,并且通过图11和图13可以看到,稀疏阵面的二维FIB方向图与原方向图基本相同。

表2给出了不同的约束门限Δa,对应二维均匀面阵抽头稀疏的个数、方向图误差Bs(f,U,V,Δa)、旁瓣电平和频域一致性均方误差,与一维均匀线阵的变化趋势一致,这里不再赘述。

表2　二维FIB稀疏约束门限对方向图性能的影响

5结论

FIB能够有效的解决宽带波束形成频率不一致的问题。本文就低旁瓣可控零陷的FIB进行了研究,通过增加等旁瓣原型滤波器和角度区域的约束,达到低旁瓣、零陷可控的目的;通过增加时域抽头稀疏优化,在保证低旁瓣零陷可控FIB方向图的情况下,达到降低运算量的目的。仿真结果验证了本文方法的正确性和有效性。本文提出的零陷可控的低旁瓣FIB宽带波束形成方法在一定程度上解决了宽带波束形成抗干扰的问题,但是该方法需要的阵元数和时域延时抽头数量要求较高,且形成的方向图波束宽度有一定地展宽,波束增益下降,仍需要进一步完善,另外自适应零陷生成技术也有待进一步研究。

参考文献：

[1] Wen S L, Yuan Q, Qin Z Y. Design criteria and development trend of wideband phased array radar[J].SystemsEngineeringandElectronics,2005,27(6):1007-1011.(文树梁,袁起,秦忠宇.宽带相控阵雷达的设计准则与发展方向[J].系统工程与电子技术,2005,27(6):1007-1011.)

[2] Wyne S, Haneda K, Ranvier S, et al. Beamforming effects on measured mm-wave channel characteristics[J].IEEETrans.onWirelessCommunications, 2011, 10(11): 3553-3559.

[3] Li N, Tang J, Peng Y N. Study on the beamfroming issues of broadband phased array radar[J].SystemsEngineeringandElectronics, 2008, 30(3): 452-454. (李宁, 汤俊, 彭应宁. 宽带相控阵雷达中波束形成问题的研究[J].系统工程与电子技术, 2008, 30(3):452-454.)

[4] Somasundaram S D. Wideband robust capon beamforming for passive sonar[J].IEEEOceanicEngineering, 2013, 38(2):308-322.

[5] Bucris Y, Cohen I, Doron M A. Bayesian focusing for coherent wideband beamforming[J].IEEETrans.onAudioSpeechandLanguageProcessing, 2012, 20(4):1282-1296.

[6] Zhao Y, Liu W. Robust wideband beamforming with frequency response variation constraint subject to arbitrary norm-bounded error[J].IEEETrans.onAntennasandPropagation, 2012, 60(5): 2566-2571.

[7] Wang B H, Hui H T, Leong M S. Optimal wideband beamforming for uniform linear arrays based on frequency-domain miso system identification[J].IEEETrans.onAntennasandPropagation, 2010, 58(8):2580-2587.

[8] Liu W. Adaptive wideband beamforming with senor delay-lines[J].SignalProcessing, 2009, 89(5):876-882.

[9] Liu W. Blind adaptive wideband beamforming for circular arrays based on phase mode transformation[J].DigitalSignalProces-sing, 2011, 21(2):239-247.

[10] Zhao Y, Liu W, Langley R J. Adaptive wideband beamforming with frequency invariance constraints[J].IEEETrans.onAntennasandPropagation, 2011, 59(4):1175-1184.

[11] Seynejad R M. Design pf an adaptive wideband beamforming alogrithm for conformal arrays[J].IEEECommunicationsLetters, 2014, 18(11):1955-1958.

[12] Liu Y Q, Yao J P, Yang J L. Wideband true-time-delay unit for phased array beamforming using discrete-chirped fiber grating prism[J].OpticsCommunications,2002,207(1/6):177-187.

[13] Doron M A, Nevet A. Robust wavefield interpolation for adaptive wideband beamforming[J].SignalProcessing,2008,88(6): 1579-1594.

[14] Seydnejad S R, Ebrahimi R. Broadband beamforming using laguerre filter[J].SignalProcessing,2012,92(4):1093-1100.

[15] Byrne D, Craddock I J. Time-domain wideband adaptive beamforming for radar breast imaging[J].IEEETrans.onAntennasandPropagation, 2015, 63(99):1725-1735.

[16] Liu W, Weiss S. Design of frequency invariant beamformers for broadband arrays[J].IEEETrans.onSignalProcessing, 2008, 56(2): 855-860.

[17] Sekiguchi T, Karasawa Y. Wideband beamspace adaptive array utilizing FIR fan filter for multibeam forming[J].IEEETrans.onSignalProcessing, 2000, 48(1):277-284.

[18] Liu W, Weiss S.Widebandbeamformingconceptsandtechniques[M]. New York: Wiley, 2010.

[19] Liu W, Weiss S. Frequency invariant beamforming for two-dimensional and three-dimensional arrays[J].SignalProcessing, 2007, 87(11):2535-2543.

[20] Zhao Y, Liu W, Langley R J. Design of frequency invariant beamformers in subbands[C]∥Proc.oftheIEEE/SPWorkshoponStatisticalSignalProcessing, 2009: 201-204.

[21] Zhao Y, Liu W, Langley R. Application of the least squares approach to fixed beamformer design with frequency-invariant constraints[J].IETSignalProcessing, 2011, 3(5):281-291.

[22] Wang Y L, Ding Q J, Li R F.Adaptivearrayprocessing[M]. Beijing:Tsinghua University Press, 2009. (王永良,丁前军,李荣锋.自适应阵列处理[M].北京:清华大学出版社,2009.)

张书瑞(1990-),男,博士研究生,主要研究方向为宽带自适应波束形成。

E-mail:king001zsr@hotmail.com

马晓峰(1981-),男,讲师,博士研究生,主要研究方向为阵列信号处理、MIMO雷达信号处理。

E-mail:maxiaofeng@njust.edu.cn

盛卫星(1966-),男,博士研究生导师,博士,主要研究方向为阵列天线、智能天线、目标电磁散射特性建模及其应用。

E-mail:shengwx@njust.edu.cn

韩玉兵(1971-),男,博士研究生导师,博士,主要研究方向为信源信道联合信号处理、多输入多数出(MIMO)通信系统、微波系统和天线设计中的优化算法、视频/图像信号的超分辨率重建、多视点视频编码。

E-mail:hanyb@ njust.edu.cn

张仁李(1986-),男,讲师,博士,主要研究方向为雷达信号处理与恒虚警检测。

E-mail:zhangrenli_nust@163.com

Wideband frequency invariant beamforming with low sidelobes and anti-jamming nulls

ZHANG Shu-rui, MA Xiao-feng, SHENG Wei-xing, HAN Yu-bing, ZHANG Ren-li

(SchoolofElectronicandOpticalEngineering,NanjingUniversityofScience&Technology,Nanjing210094,China)

Abstract:The constraints of pattern nulling and the prototype equiripple finite impulse response (FIR) are respectively added to the original fourier transform frequency invariant beamforming (FIB) to obtain pattern of wideband FIB with low sidelobe and anti-jamming nulling. The thinned optimization of FIB coefficients is also considered to reduce the calculating complex. The simulation results verify the correctness and effectiveness of the proposed method.

Keywords:frequency invariant beamforming (FIB); wideband beamforming; anti-jamming nulling; low-sidelobe

收稿日期：2015-06-12；修回日期：2015-10-19；网络优先出版日期：2016-02-15。

基金项目：国家自然科学基金(61401207)；上海航天基金重点项目(SAST201437)资助课题

中图分类号：TN 953+.5

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.04

作者简介：

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160215.0858.002.html