道器合一*——基于分形理论的璧山规划展览馆设计解析

伍利君



道器合一*
——基于分形理论的璧山规划展览馆设计解析

伍利君

摘 要本文介绍了分形理论的概念，简述其在建筑设计中的适用性和实践概况，并以璧山规划展览馆项目为研究样本，探讨分形理论在建筑设计多个环节中的具体运用过程及策略。

关键词分形理论；自相似性；几何分形；道器合一；璧山规划展览馆

伍利君. 道器合一——基于分形理论的璧山规划展览馆设计解析[J]. 西部人居环境学刊, 2016, 31(02): 32-38.

* 国家自然科学基金资助项目（51278507）

伍利君： 重庆大学建筑城规学院，硕士研究生，wulijuncq@163.com

Abstract: The article introduces the concept of fractal theory and its nature of Tao-Qi combination, and describes its applicability and practice in architecture design. Taking the design of Bishan Planning Exhibition Hall as an example, the article aims to discuss the applying strategy and process of fractal theory in the multiple aspects of architecture design.

0 引 言

“在自然现象中显然存在着分形秩序，由于其复杂性以前被拒绝接受。位于秩序和混沌之间的中间领域的分形几何学是生命本身的原则。生命时代的建筑将在分形几何学的基础上发展。”［1］

——黑川纪章

分形是非线性科学中最重要的三个概念（分形、混沌、孤立波）之一，是研究自然界中存在的大量不规则形体特征的几何学，自其诞生以来就被逐渐广泛运用于诸多学科的研究和实践之中。在建筑学科领域，国内关于分形理论的研究还相对滞后，近年来虽有较多增长，但仍以对国外相关设计实践的归纳阐释①和对国内传统建筑文化中分形现象的分析验证②为主；在具体设计应用方面，国内研究则多集中于脱离具体建筑功能的设计探讨③，虽偶有实际工程研究也停留在理念评析层面④，尚缺乏对应用了分形理论的单个工程案例进行具体构思过程和设计手法方面的深入研究阐释。基于此，本文在阐释分形理论概念的基础上，简述其在建筑设计中的适用性与实践概况，并以璧山规划展览馆项目为研究样本，以期探讨分形理论在建筑设计多个环节中的具体运用过程及策略。

1 分形理论

1975年，曼德尔布罗特（Mandelbrot）在其法文专著《分形对象：形、机遇与维数》中首次提出分形（Fractal）的概念，随后又在1982年出版的著作《大自然的分形几何学》中对分形几何学做了进一步阐释。与研究整数维对象的传统欧氏几何不同，分形几何研究的图形具有分数维（也有整数维的特例），自相似性、递归性、层次性以及仿射变换不变性等特征。分形理论从最开始的图形研究到学科建立，再到后面的多学科应用，主要经历了3个阶段的发展，见表1。

分形是一个具有普遍意义的概念，在自然界、社会和人类思维中都存在着分形现象。分形的自相似性反映了自然界中一类物质的局部与局部、局部与整体在形态、功能、信息、时间与空间等方面具有统计意义上的自相似性［2］。它可以分为自然分形、时间分形、社会分形和思维分形四大类。自然分形包括几何分形、功能分形、信息分形和能量分形等；时间分形表示在时间轴上具有自相似的系统；社会分形指人类社会活动和社会现象所表现出的自相似现象；思维分形指人类在认识、意识上所表现出的自相似特性［3］。分形理论指出了客观物质世界的部分与整体之间的辩证关系，为人们从局部认识整体、从有限认识无限提供了新的方法论，已经被广泛地运用于地球科学、生物学、地理学、材料科学、经济学以及艺术学等学科中。

2 分形理论与建筑设计

2.1 分形理论在建筑设计中的适用性

《周易·系辞传》中提出“形而上者谓之道，形而下者谓之器”，道是乾坤和阴阳交易的法则和规律，是无形的，故称为“形而上”；而器则是依据道而生成的有形之物，称为“形而下”［4］。朱熹通过“器亦道，道亦器，有分别而不相离也”，“有道须有器，有器须有道”阐释了其中“道”与“器”之间虽有分别而又浑然一体的哲学辩证关系［5］。本文所阐释的分形理论就既包含了由自相似等特性所反映的“形而上”的客观物质世界部分与整体之间的辩证关系，也包含了由分形几何所涵盖的“形而下”的形式美学，是为道器合一。

建筑不论经历怎样的嬗变都摆脱不了空间与形式的制约。正如老子所言“当其无，有室之用”，空间只有通过限定和组织才得以呈现，而形式则通过表皮与形体等才得以具体表征，二者相互制约又相互依托。基于此，分形理论所涵盖的哲学概念和形式美学对建筑设计有相当的契合性与适用性。首先，分形理论的“道”，即局部与局部、局部与整体之间的自相似性所揭示的分形思想，在建筑设计中的运用并非偶来之物，实质上，它早在中国的传统建筑和城市设计中就已体现出来，其中，中国诸多的优秀传统城市就是一个多迭代层次、均质化和整体性的分形体。以唐长安城为例，以“城、坊、院、屋”分为四个层次，构成完美的自相似结构。其中，“墙”是分形迭代的主体，从外围最高大的城墙，到各街坊每晚需要各自关闭的坊墙，再到各家各户自己的院墙，最后是每间屋子的围合墙壁［6］。其次，分形理论的“器”，即分形几何所涵盖的分形美学，在如今日益追求细腻化、情感化、参数化的建筑表皮及形体设计中已经得到广泛运用。

2.2 分形理论在建筑设计中的实践概况

广义上讲，分形理论除了在建筑空间系统组织上的运用外，还在建筑设计上有以下两方面的具体应用。首先，一个建筑的分形维数可以被测量并作为一个评价工具。例如，国内已有学者将分形理论运用于建筑风貌的评价和控制［7］；其次，可以运用分形理论将复杂的节律予以转化并运用于建筑设计中的表皮设计、形体建构以及组织布局等多方面。例如，我们可以测量基地背后山脊的分形维数来用于指导项目中建筑节律的设计［8］。

在建筑评价方面，曼德尔布罗特曾在《大自然的分形几何学》中写到“分形的‘新几何艺术'与大师们的绘画或者布扎体系的古典建筑有着惊人的相似性”，同时又提到在建筑设计中有着截然不同的情况，“一座密斯·凡·德·罗（Ludwig Mies Van der Rohe）的建筑是对经典欧式几何的回归，而合乎潮流的布扎古典建筑则更富于分形的面貌。”［9］

表1　分形理论的发展演变过程Tab.1 the developing process of fractal theory

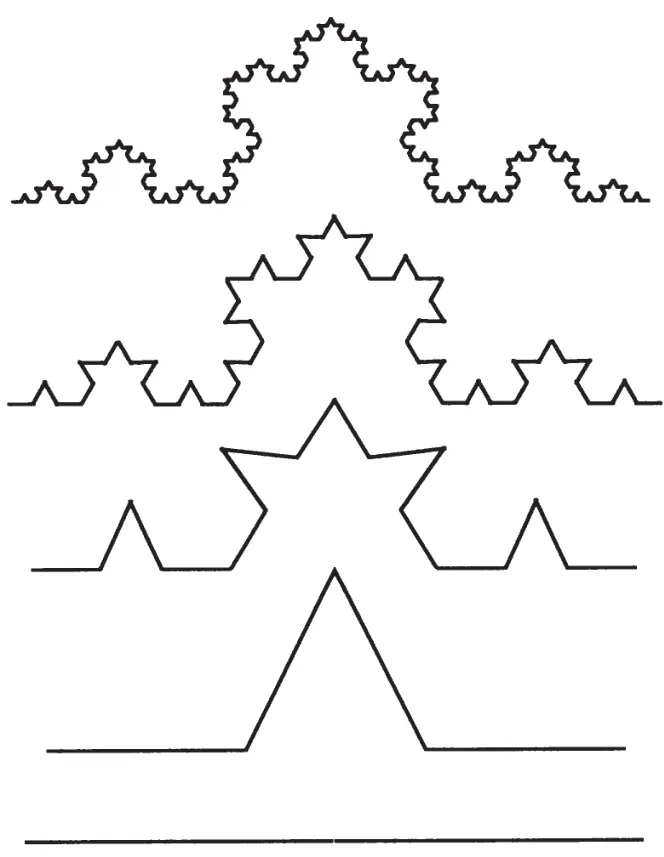
图1　冯·科赫曲线Fig.1 Von Koch curve

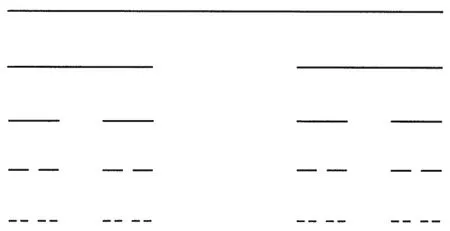
图2　康托尔三分集Fig.2 Cantor set

在建筑设计方面，从单体建筑设计到城市设计的多个环节中都有分形理论的应用。在单体设计中，建筑师们所钟爱的黄金分割就是具有自相似分形特性的比例图形（图3）；在城市设计中，罗恩·艾葛拉西（Ron Eglash）早在19世纪80年代就通过航拍图发现非洲聚落空间具有自组织的分形结构（图4-5），同时，他们的社会等级也体现在房屋的特殊分形几何结构中［10］。

在分形理论学科确立之后，众多国际先锋建筑师就开始将分形理论的理念运用到各自的建筑作品当中，例如，美国建筑师彼得·艾森曼（Peter Eisenman）的11a住宅，荷兰建筑师阿尔多·凡·艾克（Aldo Van Eyck）的阿姆斯特丹儿童之家以及日本建筑师桢文彦的东京螺旋体大厦等。

当然，分形理论的思想也被运用于时下发展势头强劲的参数化建筑设计中，在诸多参数化建筑的表皮或者形体建构上都能看到分形的特征。

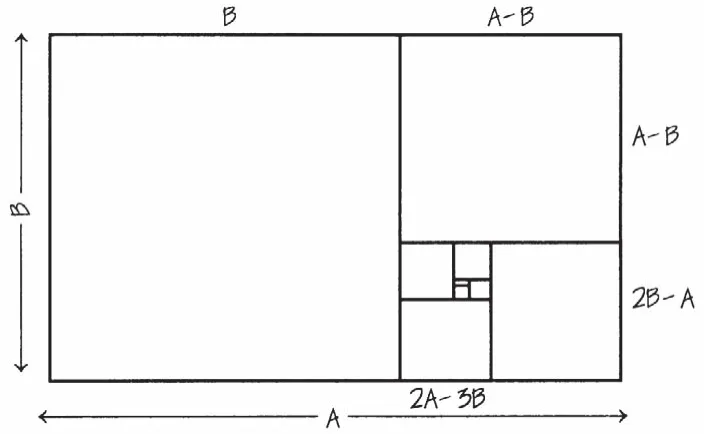
图3　黄金分割Fig.3 golden section

图4　喀麦隆洛贡比尔尼城市航拍图Fig.4 aerial view of Logone-Birni City in Cameroon

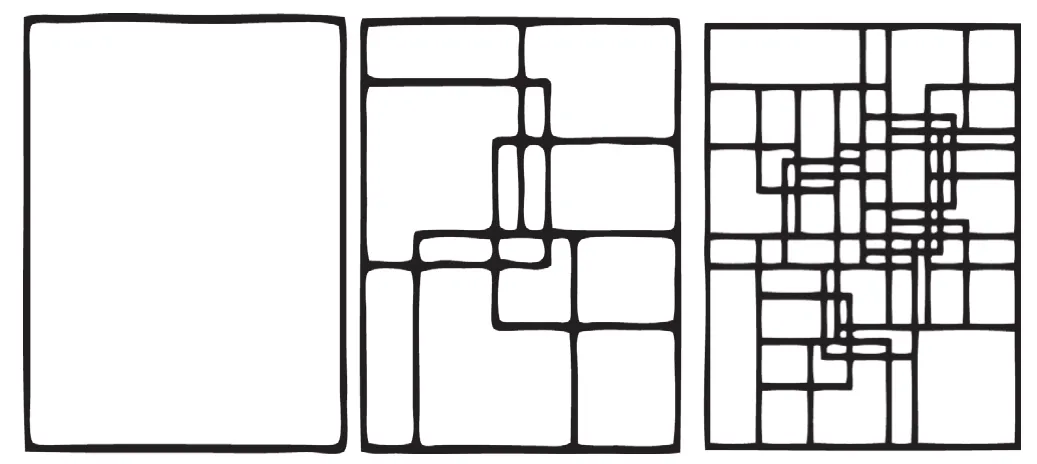
图5　洛贡比尔尼城市的前三次分形迭代模拟Fig.5 first three iterations of the fractal simul of Logone-Birni

3 分形理论在璧山规划展览馆设计中的应用

3.1 项目概况

璧山规划展览馆基址所在的璧山位于重庆主城以西，历史久远，史称“巴渝名邑”，地灵人杰，在两汉时期其境内经济发展已呈较高水平。璧山全县共有市级文物保护单位3处，县级文物保护单位43处；县境之内，还有36座古寨、95处古墓，具有深厚的历史文化底蕴。

项目基址紧临璧山老城中心区，西临秀湖，东接城市规划道路，北连北城居住区，基地内地形起伏，植被茂密，生态环境良好，能很好地体现璧山作为重庆“绿岛新区”的整体形象（图6）。项目作为璧山县规划展览馆，是展示璧山城市历史变迁、发展现状和规划远景的重要窗口以及宣传其城市规划全貌的重要载体。

图6　璧山规划展览馆Fig.6 Bishan Planning Exhibition Hall

3.2 形体设计的几何分形策略

项目基址所处环境特质明显，受到来自城市景观轴、干道景观以及水域环境等多方面的条件制约，基于上述各方作用影响，项目在设计上采取了三角形的总体布局策略（图7）。另外，场地原始条件跨山面水且植被良好，东西向有较大高差，属于典型的山地条件，应在设计中积极应对。正如生物系统中单个生命个体难以应对复杂环境而大多采取自组织的群体策略一样，巴渝地区众多传统山地村镇也多为群体建筑，体现出了退坡、吊脚、筑台、靠岩、重叠、出挑等建筑及空间特征。这样具有自组织形态的建筑群体与单个建筑个体相较而言在应对地形和气候等环境因素时具有更强的灵活性和适应性，从而更能促进建筑群体的稳定与协调。从中我们可以看出群体建筑的秩序不仅体现功能的关系，更会体现环境的作用。为更好地应对基地的高差条件，也为将建筑对周围环境的影响降到最低，方案设计中借鉴谢尔宾斯基三角形的自组织分形策略（图8-10），将建筑分解为三个体量，随山势跌落，在顺应地势的同时也融入了环境（图11）。这种体量的生成及分解方式将建筑掩映在山林之中，营造出大实大虚的情境，也创造出诸多供市民休闲的半室外空间（图12）。

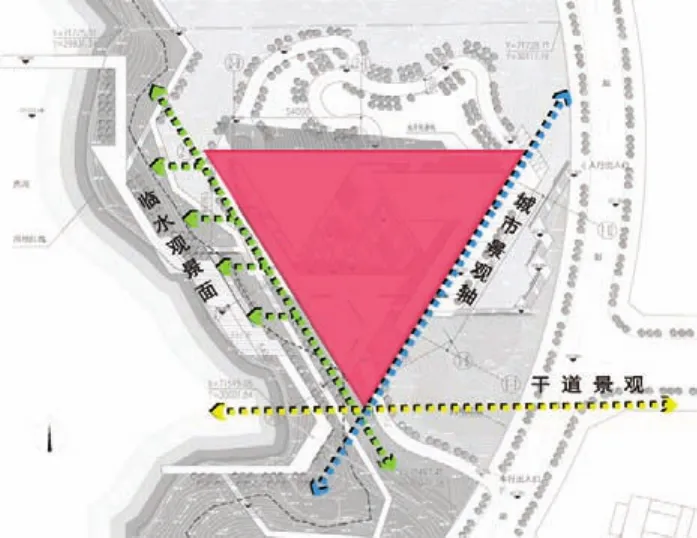
图7　总体布局策略Fig.7 overall layout strategy

凡是在自然界中客观存在的或经过抽象而得到的具有自相似性的几何形体或对象， 都称为自然分形，可以细分为几何分形、功能分形、信息分形、能量分形等［11］。自然界中的分形现象以及各学科中研究的分形，其嵌套结构一般是有限代层的，也就是说客观存在的分形体只在一定层次范围内才呈现为分形或者准分形。另外，由于系统内部及外部环境之间的涨落作用还会使系统在演化方向和演化速度上形成非均匀、非对称状态。基于此，构成璧山规划展览馆的三个体量虽然在形态上略有差异，但是形态和结构在局部与局部以及局部与整体两个方面均存在自相似性，属于几何分形。

基于分形理论， 分形体将由各个具有自相似性的相对独立部分组成，称为分形元或生成元。璧山规划展览馆选择了三角形作为基本分形元，除了上文所述的对周边环境作用力的回应外，还考虑到人类对三角形的认知概念，从中国古代山的象形文字到古埃及金字塔都代表了一种纯粹伟岸的形象，在很大程度上成为一种人类对于山体和自然崇拜的标志，它可以更易被理解也更为深刻地留在人们印象中，从而加深人们对璧山这座山水城市的记忆和感受；此外，三角形这一基本母题，也是几何的基本图案之一，具有简明性，在建筑的形体表达上能有一种地标特质，作为建筑空间的构成可以清晰地表达该项目在璧山城市建设中的重要作用，成为承接老区和展望新区的重要场所，彰显璧山城市特色。

图8　谢尔宾斯基三角形Fig.8 Sierpinski triangle

图9　建筑体量生成过程Fig.9 generation of the architecture

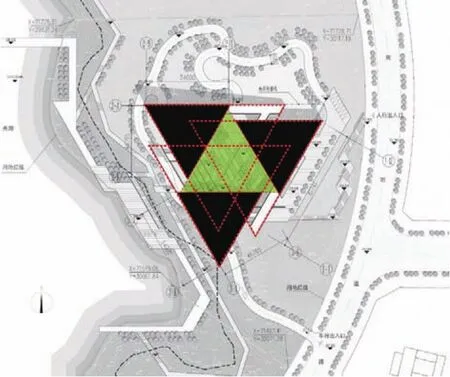
图10　建筑布局分形结构Fig.10 the fractal structure of the building arrangement

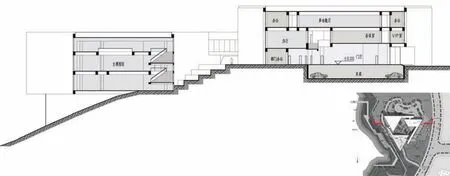
图11　剖面图Fig.11 sectional view

图12　鸟瞰图Fig.12 aerial view

3.3 功能组织的时间分形策略

璧山规划展览馆项目为综合性公建项目（图13），总建筑面积为11554.65m2，地上最大层数3层，地下4层。构成整体的3个三角形体量分别代表了不同的功能：办公、城市规划展览及市民文化展览（图14）。在参观路径的组织中，按照“过去—现在—未来”的布展时序，用一条参观路径，随体量的跌落串联起主要的展馆（图15）。观者在路径中可以不时地和庭院以及外景湖面有视线上的交流，最后，坐电梯回到入口广场的上方时还可以回望整个过程，眺望远处正在兴起的新城，引发对未来无限的想象。

凡是在时间轴上具有自相似性的现象或研究对象，称为时间分形。时间分形表明时间轴上某一节段的体验或事件和其他节段以及整个时间段具有自相似性，如生物学中的海克尔生物重演律⑤所表述的现象，生物个体的发育是生物种系进化过程简短而又迅速的重演。对于时间节律，德国科学家魏尔曾说过一段耐人寻味的话：“在一维时间中，等间隔的重复是节律的音乐原则。当一棵苗生长时，人们可以说，它把一种缓慢的时间节律翻译成了一种空间的节律。”［12］除了我们所熟知的三维空间中出现的空间分维以外，在时间中也存在时间分维。

在建筑层面上，展览馆3个体量的功能各不相同，但围绕共同的中庭，在线性游览路径上有着相似的内部空间，在不同的时间节段给予参观者相似的瞬时空间体验（图16），同时，各节段的空间体验又共同构成了游览者对展览馆的整体空间认知；在城市层面上，游览过程中，参观个体会完成对于展馆本身的前、中、后的参观体验，而又将在“过去—现在—将来”的布展时序中领略璧山城市建设历程的缩影。这种部分与整体在时空上的自相似性符合分形理论指出的客观物质世界部分与整体之间自相似性的辩证关系，正如英国浪漫主义诗人威廉·布莱克（William Blake）的诗句：“一沙一世界，一花一天堂。掌心握无限，须臾纳永恒。”它找到了部分过渡到整体的媒介和桥梁，揭示了部分与整体之间多层次、多维度的联系。

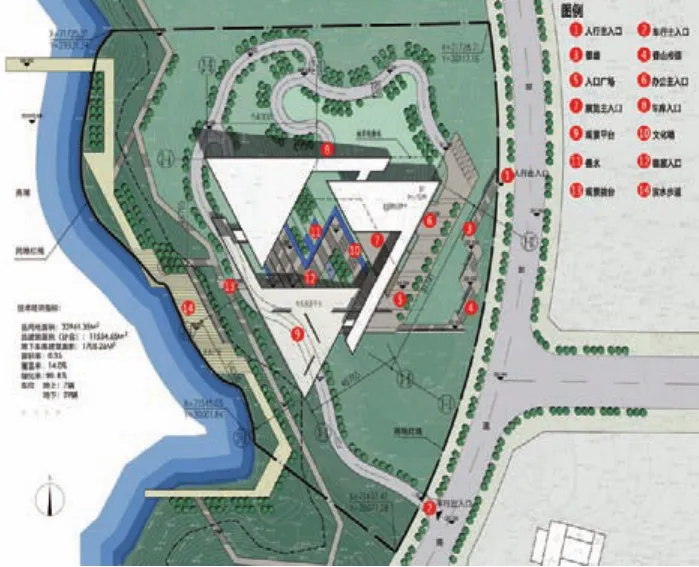
图13　总平面图Fig.13 master plan

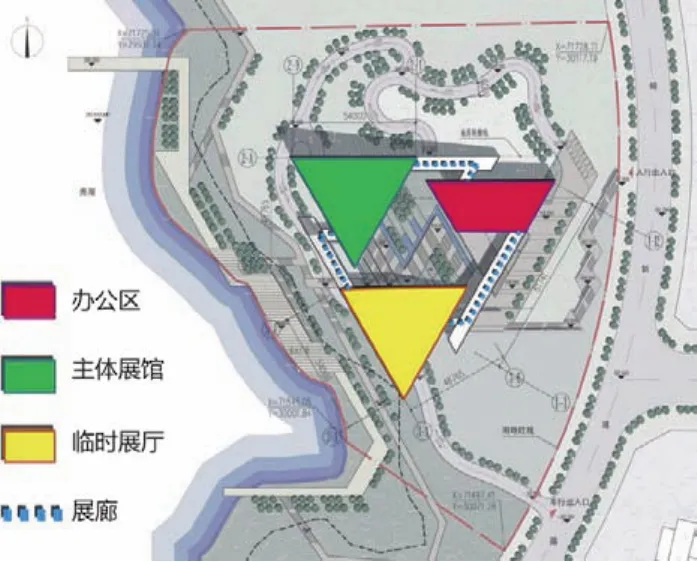
图14　功能分析Fig.14 functional analysis

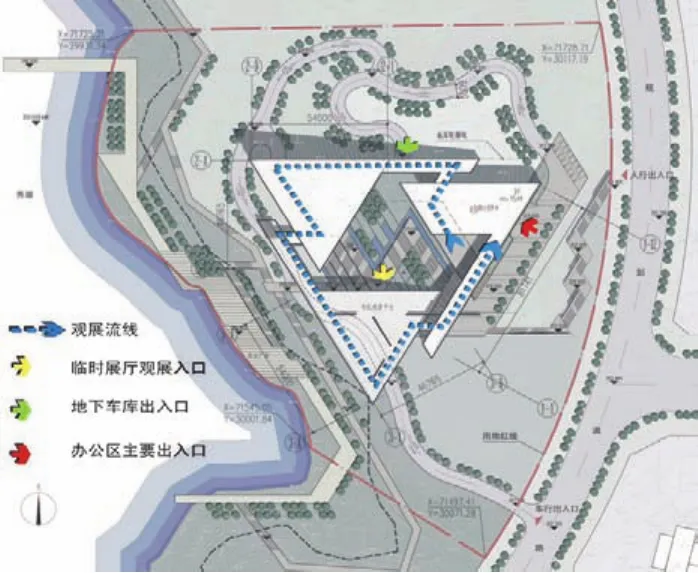
图15　观展路径Fig.15 visit route

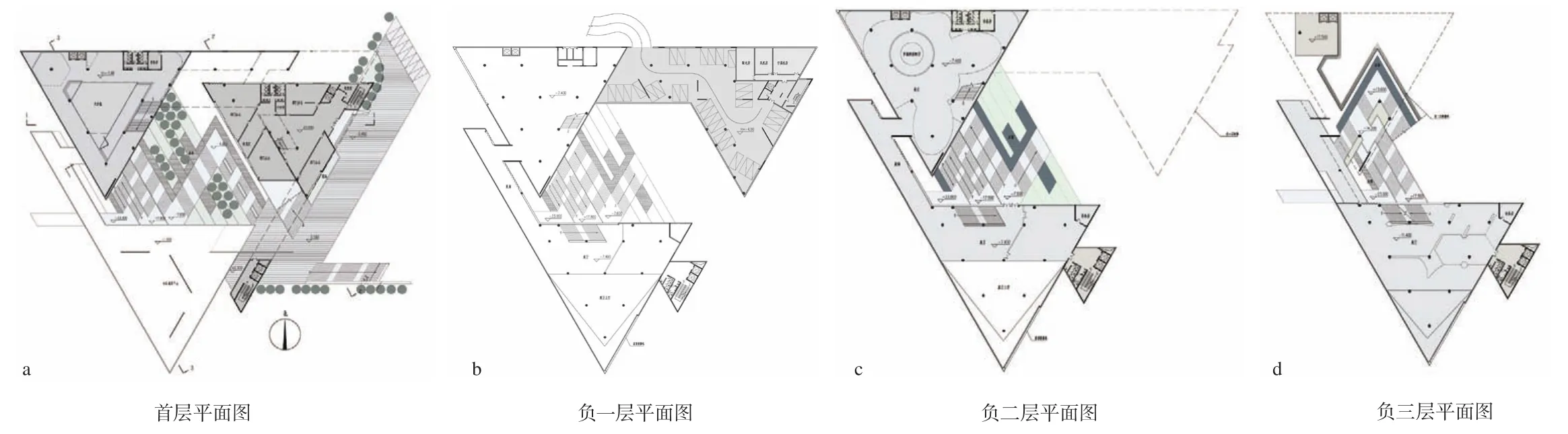
图16　主要平面图Fig.16 main floor plans of the building

3.4 装饰及景观设计的分形特征

在璧山规划展览馆的设计中采取了建筑、室内以及景观一体化的设计策略，以三角形的基本生成元作为一个设计母题贯穿于设计中。在室内的顶棚装饰、地板划分以及结构梁等设计上均采取了三角形的基本生成元符号，它们同时也被运用到馆内展陈设施的设计中（图17-18）。建筑创作只有兼顾了整体把控和细部设计两方面，才能使参观者在进入建筑空间时能不断发现蕴含整体设计意图的细节，且更易理解整个空间的设计意图，这属于思维分形的运用范畴。

图17　室内照片Fig.17 interior photo

图18　展陈设施照片Fig.18 photo of exhibition facility

当我们对于早已知道的东西表示认同，或记忆中的某个东西被唤醒时，我们会产生强烈的感情体验［13］。正是如此，当人在建筑空间环境中游走时，局部的场所或地域元素能通过思维分形来触发人的记忆，使人能更全面的认知场所，并激发其归属感与认可度（图19）。其中，展览馆的中庭浮雕，通过对群山景象简化分形维数并运用分形设计方法进行艺术重构，让参观者在局部的浮雕作品中能够识别出场地独有的场所精神和璧山特有的城市自然文化（图20）。

图19　地域元素Fig.19 regional elements

图20　中庭浮雕Fig.20 relief of the atrium

4 结 语

分形理论在璧山规划展览馆项目中的应用，除了体现出建筑本身所具有的形而下的分形美学以及群体秩序所回应的场所意识外，还作为一种设计方法和哲学思想在城市规划展览馆设计的过程中体现出相当的适宜性。一方面，自相似性是分形理论的核心，作为分形生成元的各部分具有平等的特征，这与规划展览馆作为市民参与和监督城市规划进程的场所而需要的公平、公开以及简明性是相符的；另一方面，规划展览馆是城市文化、科技、理念的集约之地与城市内在精神的展示平台，需要通过空间和功能的策划让市民在有限的参观体验环节中获得更好的城市精神以及规划发展全貌的认知，这与分形理论所揭示的局部与整体相似并反映整体的哲学思想相吻合。

分形理论被誉为大自然的几何学，它不仅是现代数学的一个新分支，还是一种新的哲学观和方法论。建筑师可以通过对分形规律的理解，从中获得更多的灵感，更好地表达建筑与自然以及建筑与人文的关系。

（致谢：感谢汤桦建筑设计事务所对本文提供的支持与帮助。）

注释：

① 此类研究如：辛善超. 当代建筑设计几何原型应用中的模块化内涵[J]. 建筑与文化, 2015(08): 103-104; 梅洪元, 王飞, 马维娜. 寒地建筑群体形态自组织适寒设计研究[J]. 建筑学报, 2015(05): 109-113; 和维. 拼接的艺术 新加坡UOL分形艺廊[J]. 室内设计与装修, 2015(05): 86-91; 杨晓丹. 非洲分形之美——评《非洲分形：现代计算模拟与本土设计研究》[J]. 国际城市规划, 2015(04): 116-123; 张广媚, 杨留位. 复杂性科学影响下的有机建筑形态解析[J]. 中外建筑, 2015(02): 76-79; 李明娟, 孟培. 分形思想在地景建筑形态生成中的转译[J]. 艺海, 2014(12): 97-99; 吴昊, 肖勤, 张善林.从分形建筑美学角度解读建筑——以日本东京表参道TOD’S大楼为例[J]. 中外建筑, 2014(07): 79-81; 沈源, 常清华. 建筑空间形式设计中的迭代及分形思想[J].住区, 2012(05): 28-35; 王科奇. 激进形式的探索——拓扑与分形[J]. 建筑科学, 2005(04): 62-67等。

② 如：韦松林. 村落景观形态实验性分形研究——以云浮大田头村为例[J]. 广东园林, 2015(02): 13-15; 常健, 叶茂. 中国传统建筑文化的分形解析[J]. 华中建筑, 2014(11): 146-150; 齐羚. 中国传统园林“理一分殊”的生态智慧探讨[J]. 风景园林, 2014(06): 45-49; 林涛, 林小松.中国古典园林的分形思想[J]. 中外建筑, 2013(09): 33-35; 董世宇. 由形态分形到秩序分形——以湖南省岳阳市张谷英村为例[J]. 华中建筑, 2012(09): 162-164; 李海英. 中国古典园林的分形美研究[D]. 东北林业大学, 2008等。

③ 如：林秋达. 子整体：跨越尺度的建筑分形现象[J]. 建筑学报, 2015(05): 99-102; 林秋达. 分形Packing算法与建筑设计[J]. 西部人居环境学刊, 2014, 29(06): 57-63; 林陌涵, 晋夜. 与分形图形结合的互承结构形式表达[J]. 建筑与文化, 2013(12): 98-99; 林秋达. 基于三维IFS算法的建筑分形设计[J]. 世界建筑, 2013(09):106-109等。

④ 如：冒亚龙, 何镜堂, 陈思翰. 自相似和谐——分形视野下的“两观三性”建筑理论解析[J]. 南方建筑, 2015(01): 84-88; 冒亚龙, 何镜堂, 郭卫宏. 分形视野下的岭南建筑学派与创作[J]. 南方建筑, 2014(01): 88-93等。

⑤ 生物重演律（recapitulation law）也叫生物发生律（biogenetic law），由1866年德国人海克尔（E. Haeckel）在《普通形态学》中提出。生物发展史可分为2个相互密切关系的部分：个体发育和系统发育。重演律指出个体发育史是系统发育史的简短而迅速的重演，即某种动物的个体发育重演其祖先的主要进化路程。

参考文献：

[1] 郑时龄, 薛密. 黑川纪章[M]. 北京: 中国建筑工业出版社, 1997: 204.

[2] 李士勇. 非线性科学及其应用[M]. 哈尔滨:哈尔滨工业大学出版社, 2011: 97-99.

[3] 张越川, 张国祺. 分形理论的科学和哲学底蕴[J]. 社会科学研究, 2005(05): 81-86.

[4] 王向清, 李芬. 道器之辨的逻辑发展[J].中南林业科技大学学报（社会科学版）, 2007(02): 27-29.

[5] 黎靖德. 朱子语类（卷75）[M]. 北京: 中华书局, 1986: 1935.

[6] 张静, 丘雷. 城市分形特征及其应用[J]. 规划师, 2002(05): 72-75.

[7] 黄海静, 陈纲. 基于分形理论的城市滨江地带风貌控制——以重庆市两江四岸地带为例[J]. 新建筑, 2015(03): 120-124.

[8] BOVILL C. Fractal Geometry in Architecture and Design[M]. Boston: Birkhauser Boston Inc, 1996: 5-6.

[9] MANDELBROT B B. The Fractal Geometry of Nature[M]. New York: W. H. Freeman and Co., 1982: 23-24.

[10] EGLASH R. African Fractals: Modern Computing and Indigenous Design[M]. New Brunswick: Rutgers University Press, 1999: 20-38.

[11] 张国祺, 李后强. 分形理论对世界认识的意义[J]. 大自然探索, 1994(01): 11-16.

[12] 李后强, 程光钺. 分形与分维：探索复杂性的新方法[M]. 成都: 四川教育出版社, 1990: 119.

[13] 尼科斯·A·萨林加罗斯. 建筑论语[M].吴秀洁, 译. 北京: 中国建筑工业出版社, 2010: 136.

图表来源：

图1、3：BOVILL C. Fractal Geometry in Architecture and Design[M]. Boston: Birkhauser Boston Inc, 1996: 2.

图2：BOVILL C. Fractal Geometry in Architecture and Design[M]. Boston: Birkhauser Boston Inc, 1996: 10.

图4-5：EGLASH R. African Fractals: Modern Computing and Indigenous Design[M]. New Brunswick: Rutgers University Press, 1999: 22.

图6、17-20：吴洁、李鹏飞拍摄

图7、9-16：深圳汤桦建筑设计事务所有限公司提供的璧山规划展览馆方案设计文本

图8：摘取自网页: http://the-ncity.livejournal. com/7922.html.

表1：作者整理绘制

（编辑：曾引）

Tao-Qi Combination —The Analysis of the Design of Bishan Planning Exhibition Hall Based on the Fractal Theory

WU Lijun

Keywords:Fractal Geometry; Self-Similarity; Mathematical Fractal; Tao-Qi Combination; Bishan Planning Exhibition Hall

中图分类号TU242.5

文献标识码B

文 章 编 号2095-6304（2016）02-0032-07

DOI:10.13791/j.cnki.hsfwest.20160208

作者简介

收稿日期：2015-08-25