基于PLS特征筛选和改进结构PNN的步态识别

袁　娜，刘　沛

(1.唐山学院 智能与信息工程学院，河北 唐山 063020；2.河北能源职业技术学院 机电工程系，河北 唐山 063000)



基于PLS特征筛选和改进结构PNN的步态识别

袁娜1，刘沛2

(1.唐山学院 智能与信息工程学院，河北 唐山 063020；2.河北能源职业技术学院 机电工程系，河北 唐山 063000)

摘要：采集单侧大腿截肢患者髋关节有代表性的加速度信号(双轴)和角速度信号，并同时采集足底压力信号，进行多运动模式识别，经信号预处理提取出特征参数，利用偏最小二乘法(PLS)进行特征筛选，最后利用改进的概率神经网络(PNN)步态模式识别和分类，实现对下肢假肢在行走、上下坡、上下台阶的不同运动模式的有效识别。

关键词：步态识别；偏最小二乘法；概率神经网络；先验变量

0引言

随着科技的进步，人们对生活质量的要求越来越高，肢体残疾人士更希望参与并融入社会生活，这就要求假肢的设计更加人性化、智能化。动力型假肢是今后假肢的发展方向[1]，而步态识别将是关键问题，只有识别出基本的步态(如上下楼梯、上下坡及平地行走)才能对假肢进行有效的控制，从而在行走时提供有效动力，满足肢残人士的正常生活需要。

步态识别的方法很多，比如利用隐马尔科夫模型[2](HMM)对运动中下肢四张肌肉的肌电信号进行步态识别；利用支持向量机(SVM)[3]的方法对多步态下肌电信号和传感器信号融合识别。随着交叉学科的出现，人工神经网络开始应用到控制研究中，并且取得了令人满意的成果。常见的人工神经网络主要有BP网络、RBF网络[4]、Hopfield神经网络、过程神经网络[5]等可供选择的模型，以及将遗传算法[6]、小脑模型[7]等与神经网络结合进行识别。基于BP网络和RBF网络在步态识别方面的应用技术已比较成熟。但选用BP神经网络，训练速度较慢，在输入样本数目较多时识别效果欠佳[8]。为了提高可靠性，采用的神经网络集成与概率融合的步态识别方法，则主要集中应用于身份识别，应用到假肢方面或对假肢识别步态起到指导作用的研究较少。针对步态自动分类提出的过程神经网络，并引入粒子群改进网络权值来克服收敛速度慢和局部最小问题的识别方法，但仍无法保障准确度，在控制假肢方面存在一定的风险。利用患者的表面肌电信号，通过支持向量机方法[9-10]进行步态识别，以及利用腿部角度传感器和足底压力传感器[11]，通过BP神经网络和有限状态机的方法进行步态识别，但因现阶段研究使用的传感器信号易受电磁干扰，准确性不高，使得多步态测量时的稳定性不易保持。而概率神经网络(PNN)作为RBF神经网络的一种变化形式[12]，通过竞争函数作为输出传递函数，由其网络特点决定其具有训练时间短、不易产生局部最优且分类正确率较高的优点。

因此笔者对传感器系统采集的步态信息进行滤波、划分步态周期、提取特征值，并利用偏最小二乘法(PLS)筛选特征值后，利用PNN构造先验变量与PNN结合识别的网络结构，与普通的PNN识别进行对比，利用这两种网络结构对比步态识别结果。

1概率神经网络

概率神经网络(PNN)是径向基神经网络的一种，其网络结构如图1所示。

图1　模式分类结构

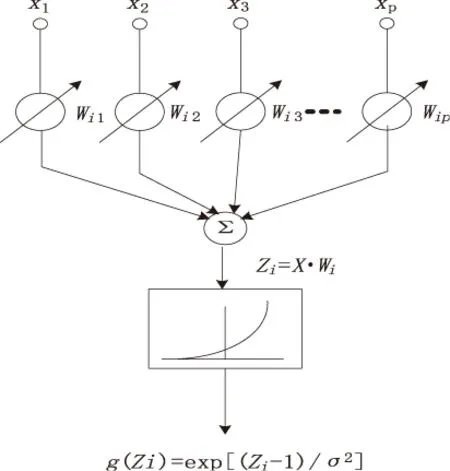
图2　模式单元

2传感器系统采集髋关节信号

针对膝上假肢设计控制源，将传感器系统固定在大腿假肢接受腔内，由加速度计(双轴)、陀螺仪和足底压力片进行步态识别。加速度计MMA7361LC用于表征人体行走过程中矢状轴(即水平面沿行走方向)和垂直轴的残肢的速度变化情况；陀螺仪ENC-03表征残肢大腿与垂直轴的角度变化情况，反应髋关节的屈、伸程度；足底压力的测量选用薄膜开关式4×4压力片，分别安装在脚掌和足跟，记录足跟离地和足趾离地的时刻，用于对加速度计和陀螺仪信号的步态周期进行采集。

2.1信号的采集

针对5种不同的步态，搭建上/下楼梯和上/下坡的实验平台。一个6级台阶、一个坡度为15°的斜坡，台阶和斜坡之间用一个平面板连接，用于进行上下楼梯和上下坡的实验，实现对路况的识别。在健康人大腿单侧的髋关节佩戴加速度计和陀螺仪，通过塑胶鞋套将足底压力片固定于脚掌和足跟处。实验者均为健康人，对5种步态分别采集15组，每组完成3个完整的步态周期，重复实验。

2.2信号预处理

2.2.1加速度计和陀螺仪信号的滤波

利用db5小波进行7层滤波[13]，以平地行走传感器信号为例，得到滤波前后的图形如图3所示。从图中可以看出滤波效果明显，滤除掉了高频噪声，而没有影响原波形的走势，保留了原来的信号特征，图形呈现明显的周期性。

图3　平地行走信号滤波前后对比图

2.2.2足底压力

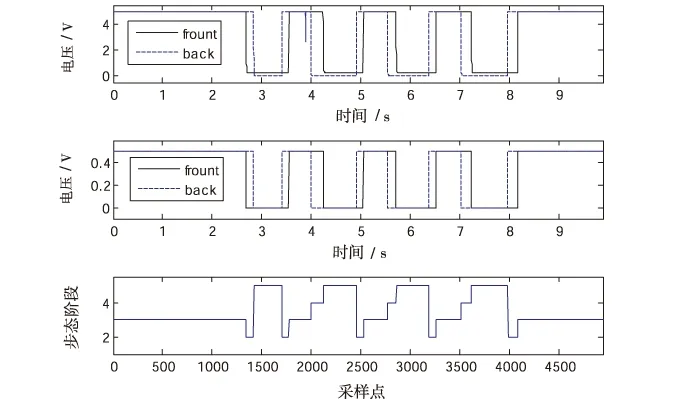
图4　足底压力信号归一并划分步态周期

对于输出高低电平的足底压力信号，进行归一化处理，将取值设定为0或0.5的高低电平，当脚掌和足跟压力均为0时，表示步态处于摆动期；当足跟有压力，脚掌压力为0时，表示步态处于支撑前期；当脚掌和足跟均有压力时，表示步态处于支撑中期；当脚掌有压力，足跟压力为0时，表示步态处于支撑末期。以此作为划分步态周期的标准。设定步态阶段用数字表示，其中2表示支撑前期，3表示支撑中期，4表示支撑末期，5表示摆动期。得到的足底压力信号归一处理后足底压力信号和表征步态阶段的梯形图如图4所示。2.2.3提取特征值

人体由静止开始运动的过程，从步态周期划分来说是先从支撑末期开始，进入摆动期，而后从支撑前期开始完整的步态周期，而由于支撑末期时间较短，信号的特征不明显，因此根据得到的5种步态传感器图形，通过前后脚掌压力划分步态周期后，提取摆动期和支撑前期的特征值：分别为一个步态周期中陀螺仪支撑前期和摆动期平均值、方差和标准差，用符号表示为averISg，averSPg，varISg，varSPg，stdISg，stdSPg；支撑前期和摆动期水平方向加速度信号平均值、方差和标准差，用符号表示为averISa1，averSPa1，varISa1，varSPa1，stdISa1，stdSPa1；支撑前期和摆动期竖直方向加速度信号平均值、方差和标准差，用符号表示为averISa2，averSPa2，varISa2，varSPa2，stdISa2，stdSPa2；摆动期3个传感器的最大值，用符号表示为maxSPg，maxSPa1，maxSPa2；摆动期的面积特征值，分别为陀螺仪、加速度计水平方向和加速度计竖直方向在摆动期前50个点和100个点对应的3个传感器信号的增面积×10倍，用符号表示为S1，S2，S3，S4，S5，S6，分别和x轴围成面积(梯形)/2.5倍，用符号表示为S7，S8，S9，S10，S11，S12，共33个特征值。

图5　陀螺仪面积特征值示意图

面积特征值的计算图形如图5所示。图中以陀螺仪信号为例，假设截取的x轴的长度为100个采样点，说明S2和S8的意义：S2表示在摆动期开始至100个采样点，陀螺仪信号相对于摆动开始点的增加的面积，为了使数值便于比较，将面积扩大10倍得到S2，对应若是50个采样点，得到S1；S8表示与y=0即x轴，在摆动期开始到100个采样点期间围成的增量面积，除以2.5后得到S8，对应50个采样点，得到S7。3PLS筛选特征值

偏最小二乘法(Partial Least Squares method，简称PLS)是一种新型的多元统计数据分析方法[14]，由S.Wold和C.Albano等人在1983年首次提出。偏最小二乘法把模型式的方法和认识性的方法有机地结合起来，它通过最小化误差的平方和找到一组数据的最佳函数匹配。用最简的方法求得一些绝对不可知的真值，而令误差平方之和为最小。在一个算法下同时实现回归建模(多元线性回归)、数据结构简化(主成分分析)以及两组变量之间的相关性分析(典型相关分析)。

利用Matlab编写PLS程序，特征值编号，运行100步生成柱状图，分3种情况对特征值进行筛选。

3.1所有特征值进行筛选(摆动期和支撑前期)

运行结果：

Maximum C.V.：99.9967 obtained with 19 variables(19 comp.)：32 27 30 23 25 1 22 31 20 21 6 18 8 5 10 4 12 17 26

对应的特征值为：S11，S6，S9，S2，S4，averISg，S1，S10，maxSPa1，maxSPa2，verSPa2，stdSPa2，S7，averISa2，varSPa1，averSPa1，varSPa2，stdISa2，S5

筛选结果见图6。

3.2仅考虑平地、下楼梯和下坡的特征值筛选(摆动期和支撑前期)

运行结果：

Maximum C.V.：100 obtained with 14 variables(14 comp.)：23 18 3 21 14 16 9 22 7 1 6 17 19 4

对应的特征值为：S2，stdSPa2，averISa1，maxSPa2，stdSPg，stdSPa1，varISa1，S1，varISg，averISg，averSPa2，stdISa2，maxSPg，averSPa1

筛选结果见图7。

图6　所有特征值PLS筛选结果

图7　仅考虑平地、下楼梯和下坡的特征值PLS筛选结果

3.3仅考虑上楼梯和上坡的特征值筛选(摆动期和支撑前期)

运行结果：

Maximum C.V.：99.9967 obtained with 15 variables(15 comp.)：27 21 26 32 4 28 6 19 10 23 16 31 12 14 29

对应的特征值为：S6，maxSPa2，S5，S11，averSPa1，S7，averSPa2，maxSPg，varSPa1，S2，stdSPa1，S10，varSPa2，stdSPg，S8

筛选结果见图8。

图8　仅考虑上楼梯和上坡的特征值PLS筛选结果

4改进PNN网络结构

本文的目的是利用PNN网络结构识别5种基本步态：平地行走、下楼梯、下坡、上楼梯和上坡。因此考虑PNN网络结构和筛选的特征值的特点，设计了先验变量与PNN结合识别的方法。

对于5种步态的分类实质是两大类步态的划分：第一类(包括平地行走、下楼梯和下坡)和第二类(包括上楼梯和上坡)。每一类中的步态具有相似的角度变化趋势。因此在识别步态时，可以先找到明显区分这两大类步态的显著特征值，将步态划分出两大类，再从两大类中找到到底是哪种步态。网络流程如图9所示。这样做简化了神经网络的结构，缩短了网络的搭建时间，同时也缩短了识别出准确步态的时间。

图9　先验变量与PNN结合的识别流程图

4.1训练先验变量与PNN结合的结构

比较提取的特征值特点，选定先验变量为varSPa2和averISa2，先利用先验变量与对应的特征值比较。若varSPa2<0.03，且averISa2>-0.07，则步态属于第一大类。反之，若varSPa2≥0.03，且averISa2≤-0.07，则步态属于第二大类。需要训练的神经网络PNN1和PNN2的输入特征向量和net12的输入特征向量不变，将筛选好的特征向量组成输入层矩阵分别用于训练PNN1和PNN2，并保存为网络net11.net和net22.net。

对网络进行训练，训练后的效果和误差如图10和图11所示，对于5种步态225组实验数据的识别，仅有1组下楼梯识别成下坡。

保存网络：net11.net，net22.net。

图10　net11训练结果和误差

图11　net22训练结果和误差

4.2训练传统的PNN

利用筛选后摆动期和支撑期特征值作为PNN的输入。对网络进行训练，训练后的效果和误差如图12所示，对于5种步态225组实验数据的识别，仅有1组下楼梯识别成下坡。

保存网络：net12.net。

图12　net12训练结果和误差

4.3先验变量与PNN结合的识别

将PNN1和PNN2训练好的网络net11和net22保存后，作为以后对步态数据识别的工具。分别输入原始信号，每组步态共15组，经过滤波、提取特征值、筛选特征值，利用保存的网络进行识别，识别结果如图13所示。

图13　net11和net22的识别结果

4.4传统的PNN的识别

同理，利用保存的网络net12进行识别，225组实验输入原始采集信号，提取摆动期和支撑期特征值识别，仅1组数据识别错误，识别结果见图14。

图14　net12的识别结果

4.5识别对比

将改进的PNN和传统的PNN两种网络结构，对相同的数据进行识别，识别结果和识别时间对比，如表1所示。

表1　对比识别结果和时间

5结论

利用改进的PNN和传统的PNN两种网络结构，对假肢传感器系统采集的信号进行步态识别。第一种是利用先验变量varSPa2和averISa2将运动步态分成两大类：第一类包括平地行走、下楼梯和下坡，利用筛选的摆动期和支撑前期14个特征值训练PNN1；第二类包括上楼梯和上坡，利用筛选的15个特征值训练PNN2，进行步态识别。第二种是直接利用筛选的摆动期和支撑前期19个特征值训练PNN网络。

从网络结构上看，将步态划分为两大类进行分别识别的方法，其网络结构更为简单，网络训练时间缩短。从对225组实验数据识别验证的结果中可以看出，利用先验变量和PNN结合的识别方式，在保证识别率不低于90%的前提下，识别时间短，且效果明显，平均缩短了0.19 s。因此针对步态规律性强的实验者，采用第一种识别方法优势明显。

参考文献：

[1]Unal R， Carloni R， Hekman E E G， et al. Koopman conceptual design of an energy efficient transfemoral prosthesis[C]. The 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems，2010：343-348.[2]孟明，佘青山，罗志增，等.HMM在下肢表面肌电信号步态识别中的应用[J].华中科技大学学报，2010，39：176-179.

[3]He Huang， Fan Zhang， Levi J Hargrove， et al. Continuous locomotion-mode identification for prosthetic legs based on neuromuscular-mechanical fusion[J]. IEEE Transactions on Biomedical Engineering，2011，58(10)：2867-2875.

[4]谭建辉，潘保昌.基于径向基函数神经网络的红外步态识别[J].现代计算机(专业版)，2011(5)：3-7.

[5]肖军，苏洁，郑波，等.智能仿生腿在不同路况下的步态识别系统研究[C].2007中国控制与决策学术年会论文集，2007：383-386.

[6]Chai Yanmei， Wang Qing， Jia Jingping， et al. A novel human gait recognition method by segmenting and extracting the region variance feature[C]. Proceedings-International Conference on Pattern Recognition，2006.

[7]喻洪流，钱省三，沈凌，等.基于小脑模型神经网络控制的步速跟随智能膝上假肢[J].中国组织工程研究与临床康复，2007，11(31)：6233-6235.

[8]谢林海，刘相滨.基于不变矩特征和BP神经网络的步态识别[J].微计算机信息，2007，19：279-281.

[9]Tee Connie， Kah Ong Goh Michael， Beng Jin Teoh Andrew. Personal recognition using multi-angles gait sequences[C]. Communications in Computer and Information Science，2011：497-508.

[10]Chen Lingling， Yang Peng， Xu Xiaoyun， et al. Above-knee prosthesis control based on posture recognition by support vector machine[C].2008 IEEE International Conference on Robotics， Automation and Mechatronics. Chengdu，2008：307-312.

[11]高云园，孟明，罗志增，等.利用多源运动信息的下肢假肢多模式多步态识别研究[J].传感器技术学报.2011，24(11)：1574-1578.

[12]许延伟，刘希玉.神经网络用于模式识别的几种主要方法及比较[J].信息技术与信息化，2005，4：120-123.[13]康桂文，蒋恒彪，左建章.基于小波阈值去噪理论的监测数据处理方法[J].测绘科学，2009，34(1)：117-118.[14]林燕.偏最小二乘变量筛选法及其应用研究[D].厦门：厦门大学，2010.

(责任编校：夏玉玲)

Gait Recognition Based on Partial Least Squares Method and Modified Probabilistic Neural Network

YUAN Na1， LIU Pei2

(1. College of Intelligence and Information Engineering，Tangshan University，Tangshan 063020， China；2. Department of Electrical and Mechanical Engineering， Hebei Vocational College of Energy and Technology， Tangshan 063000， China)

Abstract：The authors of this paper propose a method of identifying the different motion patterns of artificial legs walking on the level ground， down or up stairs and slopes by first collecting the typical acceleration signal(dual-axis) and the angular velocity signal of the hip joint of the patients with one leg amputated， and the plantar pressure signal to recognize the motion patterns， then pre-processing the signals to extract the feature parameters and selecting them with partial least squares (PLS) method， and finally finding and classifying the gait pattern through improved probabilistic neural network (PNN).

Key Words：gait recognition； partial least squares method； probabilistic neural network； priori variable

作者简介：袁娜(1988-)，女，河北唐山人，硕士，主要从事计算机智能控制研究。

中图分类号：TP183

文献标志码：A

文章编号：1672-349X(2016)03-0047-06

DOI：10.16160/j.cnki.tsxyxb.2016.03.014