紧扣算理 指导计算——“两位数乘两位数”教学设计

◇汪 涛 陈 云

紧扣算理 指导计算
——“两位数乘两位数”教学设计

◇汪 涛 陈 云

设计思路

培养学生的计算能力是小学数学教学的核心任务之一。计算能力强的重要标志是对计算过程的深刻理解。

“两位数乘两位数”的主要依据是乘法分配律。以教材情境给出的题目为例：14×12＝14×（10＋2）＝14×10＋14×2＝（10＋4）×12＝10×12＋4×12＝10×10＋10×4＋10×2＋4×2。这一计算过程的实质是乘法分配律复合运用的过程，教材通过点子图进行了详细的分解。

因此，教师可以借助点子图，确立“以算理指导计算”的整体教学思路，努力做到四个“顺应”，优化教学过程，落实“会学”目标。

一、顺应认知的“同化”规律

“同化”是学生构建认知结构的方式之一。顺利实现“两位数乘两位数”对知识的“同化”，需要教师采取切实有效的措施，激活学生原有的认知结构。如通过口算、笔算回顾乘数是一位数的乘法计算方法，回顾上一课时运用的点子图和方格图得出的计算方法等，有目的地提取原有的认知结构，为“同化”铺平道路。

二、顺应儿童的“好胜”心理

教学应该顺应儿童的心理特点，以教师“引导”地教，促进学生“主动”地学。如在进行相关的复习、铺垫后，可直接抛出问题：“你能用竖式计算14×12吗？”让学生“八仙过海，各显神通”。

当学生结合一位数乘法直接得出下面算法时（如下图），教师应鼓励学生结合上节课所用的点子图，想到这个计算过程是14×10＋14×2或10×12＋4×12，并鼓励学生想办法把这个过程用竖式表示出来，以修正学生的错误想法，得到正确的竖式书写过程。

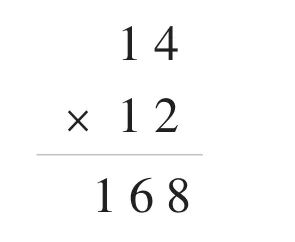
这样，学生就在“好胜”心理的驱使下，自主进行算理的探究，培养了学生的迁移、分析、综合能力。

三、顺应思维的“概括”过程

概括水平是衡量思维能力的标志。“两位数乘两位数”要思考的内容很多，我们认为直指知识内涵的核心问题有以下几个。

1.求14×12的积要分哪几步计算？

2.每一步分别算什么？

3.为什么用十位上的数去乘，积的末尾要和十位对齐？

思考这些问题的目的在于，把“拆分求积”的分步过程上升到综合竖式计算。教师在引导学生思考的过程中，要依托具体的情境和学生分步解答的思维原型，以乘法分配律为指导，结合点子图、方格图，展示思维的概括过程，揭示竖式由“分”到“合”的演变，帮助学生理解算理。

四、顺应教材的“逻辑”顺序

学生初学“乘数是两位数的乘法”时，往往只把相同数位上的数相乘，而漏乘某一位；或把积的位置写错；或把某一位相乘算成相加……针对学生学习的实际，北师大版教材采取了相应的措施：

1.强化对计算过程的理解。如“练一练”的第1题再次结合点子图让学生说说竖式每一步的意思（如下图）。

2.手、脑、口并用，强化对计算过程的理解。如“算一算”中要求和同伴说一说计算的过程。

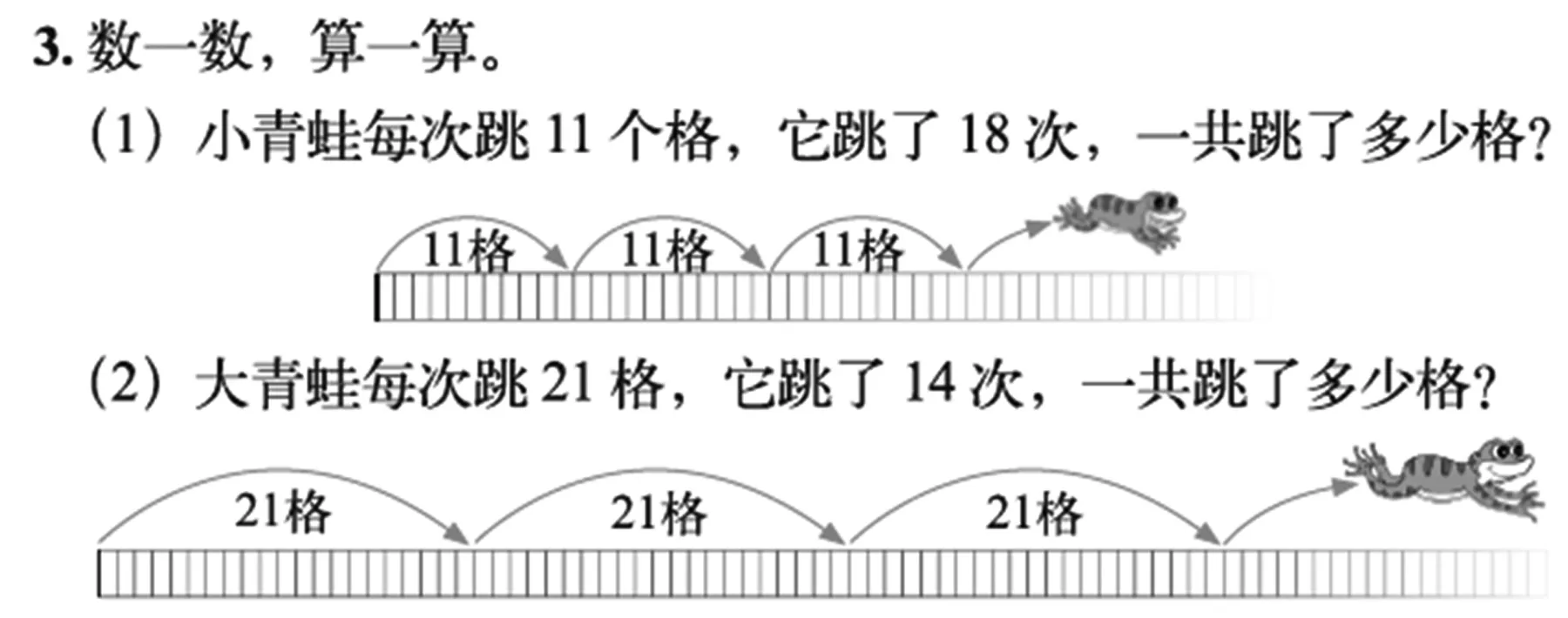
3.结合有趣的青蛙跳，进一步理解乘法的意义与竖式计算过程的联系。如“练一练”第3题（如下图）。

设计过程

一、温故——孕伏算理

1.口算：30×6 20×18 7×50 15×40

2.用竖式计算：26×7 143×6

3.出示“队列表演（一）”的情境图，让学生说说是怎样借助点子图和方格图算出结果的。

4.提问：你能用竖式计算14×12吗？

二、发散——探究算理

1.尝试。结合一位数的乘法，让学生独立尝试用竖式计算14×12。

2.反馈。展示学生的算法，并让学生说一说是怎么想的。

3.发散。提问：你认为应怎样列竖式？一位数乘两位数、三位数都是一步就能算出结果的，那两位数乘两位数呢？需要几步计算？先算什么？再算什么？

三、深究——理解算理

1.启思：结合点子图，说一说如何把“拆分求积”的思考过程转化为竖式计算。

2.导读：①从点子图看，我们是分几步计算14×12的积的？②每一步分别算的是什么？③用“先算、再算、然后算”的模式说一说计算过程。

3.观察：竖式计算与点子图有什么联系？你愿意用哪种方法计算？说说自己的想法。

4.比较：两位数乘两位数与一位数乘法有什么联系？有什么区别？

5.思考：在口算 10乘 14时，我们是怎么算的？“0”在这里起什么作用？为什么4要写在十位上？

6.归纳：两位数乘两位数笔算方法和过程。

四、变练——消化算理

1.补充完成下面的计算过程。

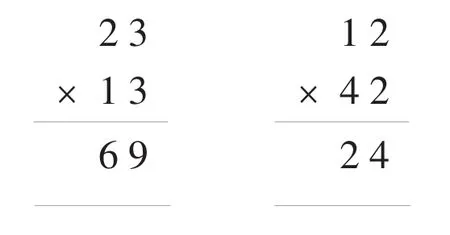
2.学校买了31把椅子，每把椅子的价钱是12元。根据下面的竖式在括号里填数。

3.反馈练习：完成课本上“练一练”中的习题。（略）

（作者单位：安徽怀宁县教研室，怀宁县振宁学校）