“圆的面积”教学实录及思考
2016-06-19陈金飞
◇陈金飞
“圆的面积”教学实录及思考
◇陈金飞

一 提供观察情境,为建立空间观念作铺垫
师:(出示动画:一只被绳子拴着的羊在草地上转一圈,如图1)用数学的眼光观察这个画面,求羊活动的范围有多大,就是求圆的什么?

图1
生:圆的面积。
师:如果这只羊想要扩大它的活动范围,你能帮它想个办法吗?
生:可以把绳子拉长。
师:(课件演示拉长绳子,羊运动一周成一个新的圆,如图2)圆的面积变大了,说明圆的面积和什么有关?
生:圆的面积和半径有关。

图2
师:那圆的面积和半径之间会有怎样的关系呢?让我们带着这个问题开始今天的探究之旅。
教后畅想:创设羊吃草的情境,揭示圆形区域的大小取决于绳子的长短,从而使学生自己抽象出“圆面积的大小是由圆的半径决定的”。
二 创设操作情境,建构空间观念
1.回顾相关知识,唤起经验,铺垫探究新知之基。
师:大家回顾一下,我们学过哪些平面图形的面积?
生:我们学过长方形、正方形、三角形、梯形、平行四边形的面积。
师:那还记得我们是怎样推导出这些面积计算公式的吗?
生:长方形的面积计算公式是用数方格的方法推导出来的,平行四边形是转化成长方形推导出它的面积计算公式的。
生:三角形和梯形是用两个完全一样的图形拼成一个平行四边形,走的也是转化之路。
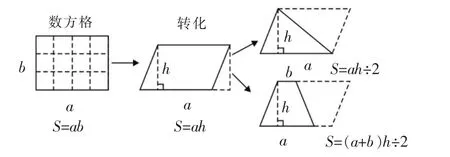
图3
师:在回顾旧知的过程中,陈老师有一个疑惑:我们一开始是用数方格的方法来推导面积计算公式,那么往后为什么走的都是转化之路呢?
生:因为如果用数方格的方法来测量三角形或平行四边形的面积,方格可能有的多出一些,有的少一些,没法准确地测量。
教后畅想:用方格度量图形的面积,是基于面积的意义,但用来测量平行四边形等图形的面积时已感受到不精确、不方便,因而凸显用转化的方法更为简捷。而圆面积计算公式的推导是小学教材中实现“化曲为直”的唯一题材,在有限的教学时间里,如何实现“化曲为直”才是我们应放大的视角。
2.呈现学习困境,引发矛盾,积蓄思维突破能量。
师:那你们打算用什么方法研究圆的面积?
生:我觉得应该用转化法,因为如果用数方格的方法,方格会多出来,而且还有一些方格直接露在外面,根本没有进去。
师:如果圆的边线变直了,测量就变得方便、精确了。明白了这点,接下来咱们就想办法把曲变直。
(板书:化曲为直。从1号信封中取出圆片,四人小组一起交流。学生动手操作后,集体交流展示)
师:先观察图4这几种折的方法,有什么想法?

图4
生:折成正方形不行。
师:说说你的理由。
生:把弯曲的部分折掉了。
师:看来这种方法不行,面积变小了。再来看另外两种折的方法,你有什么发现?
生:折的次数越多,底边就会变得越平。
师:真善于观察,那为什么不继续往下折呢?
生:纸太厚了,不能再往下折。
师:看来光用折的方法,不能实现化曲为直。观察图5这两个剪拼成的图形,有什么想法?

图5
生:左面的正方形不行,这个图形变大了。
师:看来转化时不能增加图形的面积,也不能减少图形的面积。观察右边这个图形,看有什么不足?
生:底边不平,弧线太弯了。
师:受折的启示,是否可以让底边变得平直些呢?
生:如果分割的份数多一些,拼出的图形底边会变得平直一些。
3.感悟数学思想,分割转化,实现极限思想飞跃。
师:事实真的如此吗?借助电脑帮忙。(多媒体展示图6)

图6
师:观察图形的变化,你发现了什么?
生:随着剪的次数增加,剪出的每一份底边变得越来越平直。
师:观察力真强,把掌声送给他!发挥我们的想象力,如果继续往下分,最后会分出一个个怎样的图形呢?
(电脑演示继续分割)
生:如果无限地往下分,我觉得会变成一个个很小的“三角形”。
师:你认为呢?
生:越来越小,说不定那个“三角形”就没有了。
生:(反驳)不可能没有,我觉得最后会变成一根针。
师:你还有什么想法?
生:越来越小,越来越小,就变成一根线了。
师:你的想象力真强,跟数学家的想法不谋而合。看来我们继续把圆分割下去,拼出的图形底边会变得更“直”,打开2号信封,同桌合作把圆片分成8等份和16等份并进行剪拼的任务。
(生动手操作)
师:孩子们,让我们一起来观察拼出的图形,(如图7)你发现了什么?

图7
生:我觉得它们越来越像平行四边形。
师:你从哪儿看出来的?
生:我发现它们上下两条边越来越平直。
师:怎样变得更直?
生:继续分割。
师:还想分割下去吗?我们请电脑帮忙,观察把圆分成32等份后,拼出的图形会有什么不同。
(电脑演示把圆分成32等份)
生:我觉得有点像长方形。
师:刚才我们说拼出的图形越来越像平行四边形,现在我们发现再往下分的话,拼出的图形越来越像——
生:长方形。
师:那怎样让它更像长方形呢?
生:继续往下分。
师:好,咱们继续往下分。(电脑演示把圆分成64等份)让我们闭上眼睛想象一下,如果无限分割这个圆片,最后会拼出一个怎样的图形呢?
(电脑出示“无限分割”)
生:我觉得最后会拼出一个长方形。
生:老师,我有一个疑惑,圆是曲线图形,边是弯的,怎么会变得直了呢?
师:你的疑惑曾困扰人们几千年,谁愿意来解释一下弯的怎么会变直了?
生:随着分的份数增多,每块图形越来越像一根线(即线段),线是没有弧度的。
师:解释得真好,感谢这名同学。孩子们,我们把圆通过无限分割,居然转化成了一个长方形,实现了“化曲为直”。这个思想,在数学发展史上是有开创性意义的。观察一下,转化后的长方形和原来的圆有什么联系呢?如何由长方形的面积计算公式推导出圆的面积计算公式呢?同桌交流,把讨论的结果记录在研究单上。
(生四人小组交流)
生:我们通过观察发现长方形的面积等于圆的面积,长方形的长等于圆周长的一半,长方形的宽等于圆的半径。
……
教后畅想:多媒体演示由圆分出的一块小扇形的变化,让学生真切地感受到无限分割后,小扇形的弧线最终变成一条“线段”。从而联想到圆经过无限分割,化曲为直,转化为长方形,从而发展空间观念。
三 回归生活情境,强化空间观念
计算羊吃到的草地最大面积。(略)
四 引入历史情境,提升空间观念
师:回顾一下,这节课你有哪些收获?
生:我学会了圆的面积计算公式。
生:我知道了圆的面积是半径平方的π倍。
生:我懂得了圆经过无限分割,最后实现化曲为直,转化为长方形。
师:(小结)是呀,重要的不只是会算圆的面积,更重要的是通过无限分割,实现化曲为直。这一思想是17世纪德国数学家开普勒开创的,下面我们一起来听一听他当初的想法。
开普勒是17世纪誉满欧洲的数学家。在他之前,数学家们都是通过从圆内接正多边形入手,让边数成倍增加,用圆内接正多边形的面积去逼近圆面积,(如图8)不仅计算复杂,而且所得结果都是近似值。开普勒受切西瓜的启发,把圆分割成无穷多个小扇形,每个小扇形都可以看成等腰三角形,每个三角形的顶点都是圆心,因而它们的高都等于圆的半径,所有底边连起来的长度之和就等于圆的周长。当把这些小三角形等积变换后,就成了一个大的直角三角形。(如图9)大三角形的面积,就是圆的面积。
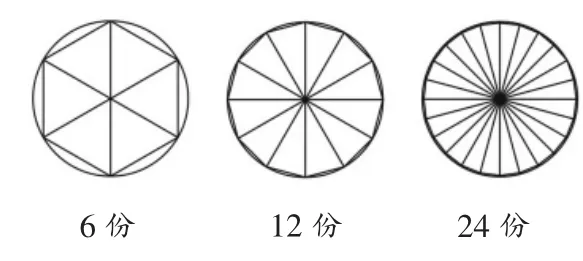
图8

图9
教后畅想:开普勒的故事丰富了问题解决的方法,拓展了学生思维,使学生进一步认识到,通过无限分割,实现化曲为直,是数学发展史上具有伟大意义的创举,是人类对固有认识的一次超越。
(作者单位:江苏启东实验小学)
