试油期间原油泡点压力计算新方法

赵洪绪　张 萍

(1. 中法渤海地质服务有限公司， 天津 300452；2. 中海油能源发展股份有限公司工程技术分公司， 天津 300452)



试油期间原油泡点压力计算新方法

赵洪绪1张 萍2

(1. 中法渤海地质服务有限公司， 天津 300452；2. 中海油能源发展股份有限公司工程技术分公司， 天津 300452)

摘要：为了准确求取油藏原油泡点压力，提出一种新的计算方法。运用该方法，对所有数据点循环分组，再分别经过线性回归后求出均方误差总和，均方误差总和越小则表示函数关系近似程度越高。

关键词：原油泡点； 压力； 线性回归； 均方误差总和； 试油

在井底流压高于饱和压力时，井下流体为单相状态。随着地层压力的不断下降，原油中的溶解气开始分离出来，井下流体为油气两相共存的状态。为了准确求取油藏原油泡点压力，本次研究将探讨一种新的计算方法。运用该方法，对所有数据点循环分组，再分别经过线性回归后求出均方误差总和，均方误差总和越小则表示函数关系近似程度越好。

1求取原油泡点压力的一般方法

1.1井下流体高压物性取样

地层原油高压物性(PVT)是确定油藏类型、制定油藏开发方案和进行油藏工程计算必不可少的重要参数，是计算油田储量、选择油井工作制度的基础[1]。在井底流压高于饱和压力(即泡点压力)时，地层原油里面溶解有大量的天然气，井下流体为单相的物理状态，这时进行井下 PVT取样可获得高质量并且有代表性的井下样品。

试油期间，在终关井期过后用小油嘴引流[2]，测试层原油在井下处于单相流动状态，待流动正常后进行井下PVT取样。到地面时，取样器中的地层流体通过转样泵转至具有保压功能的样瓶中[3]。为了得到地层温度下地层原油体积和压力的关系数据及泡点压力数据，现场需要对井下PVT样品进行转样操作。将装有井下PVT样品的样瓶安装到微型转样泵上，加温；然后进行系统加压，压力高于取样地层压力的25%；再摇动转样瓶，使油气混匀；接着观察系统压力降，通过压力变化判断PVT样品是否以单相状态存在，若压力下降则继续打压，直至压力不降为止[4]；随后不断加大转样瓶中原油样品的体积，使原油样品的压力不断下降，原油的物理状态逐渐发生改变，原油中的溶解气开始分离出来，原油样品由单相的物理状态变为油气两相共存的物理状态。在这一过程中可得到若干组体积和压力的对应数据，根据这些数据可现场求取原油样品的泡点压力。

1.2现场实例

DST NO.1井试油作业过程中，在2 097 m深处进行井下PVT取样，到地面后对样品进行转样及相关操作，得到9组压力与体积数据。表1所示为DST NO.1井下PVT样品相关数据。

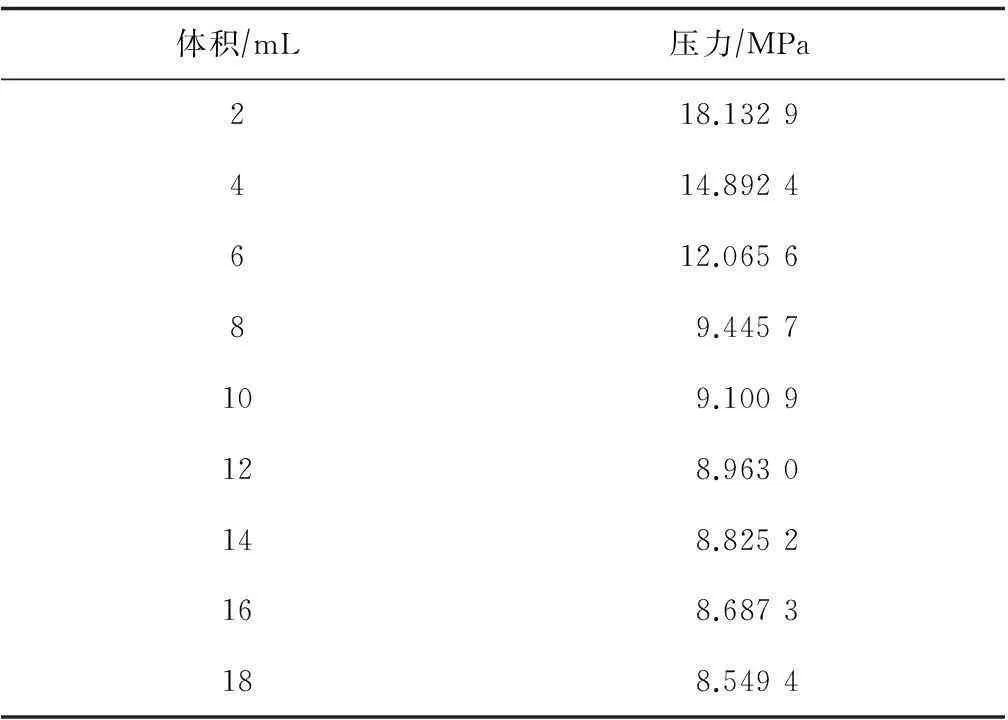
表1　DST NO.1井下PVT样品相关数据

通过目测将数据分成2组，每一组代表一种状态；再分别对2组数据进行线性回归；最后算出交点即为现场求取的原油泡点压力，数值为9.238 8 MPa。图1所示为原油p-v关系曲线。

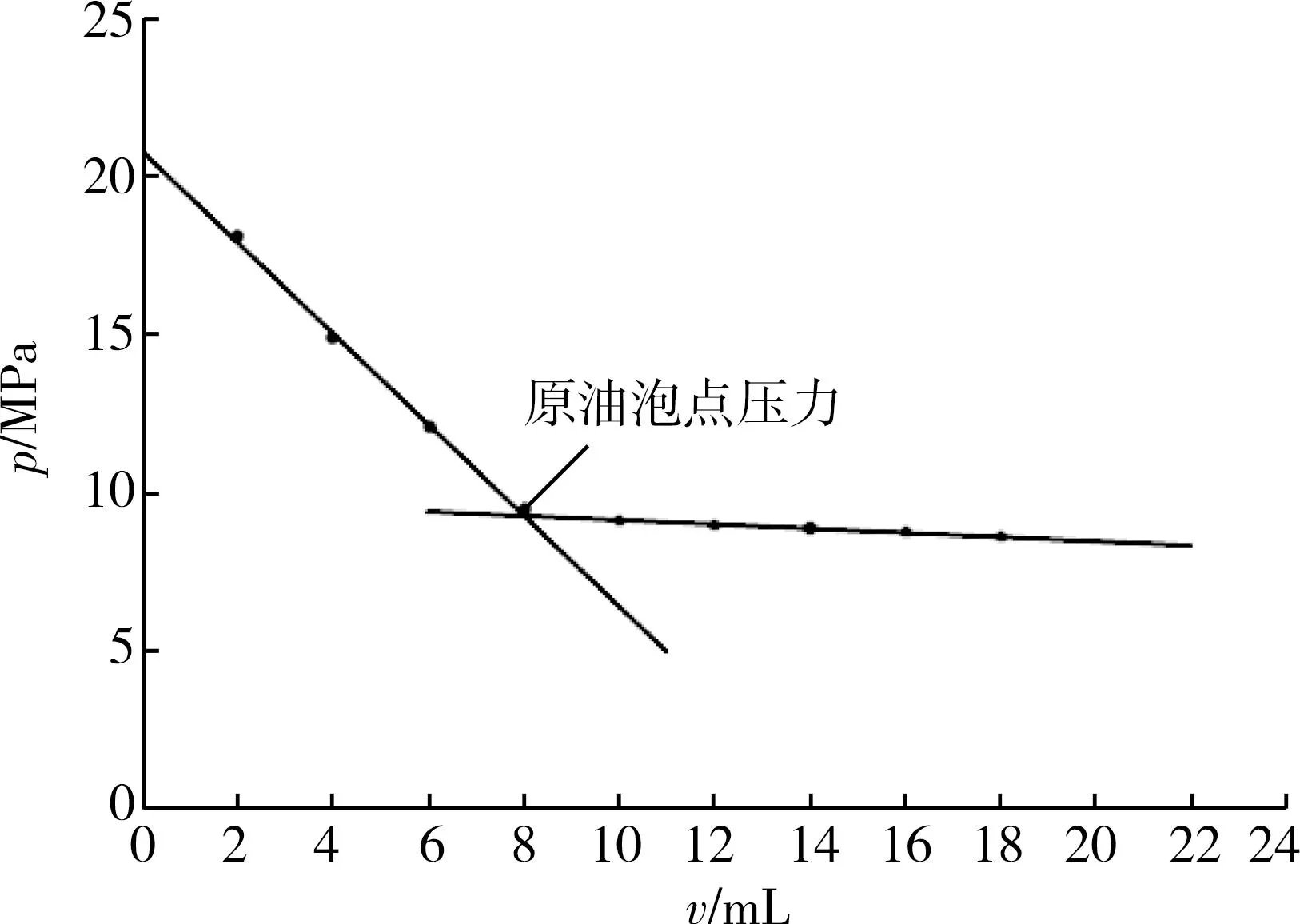
图1　原油p-v关系曲线

2原油泡点求取新方法 —— 临界点算法

与上述方法不同，新方法引入了临界点的概念，可以更加准确地求取状态变化瞬间的数据。

2.1数据循环分组

根据两点确定一条直线的定理，对表1中的9组数据进行循环分组， 有 6种情况，分别见表2 — 表7。

表2　数据点2-7分组

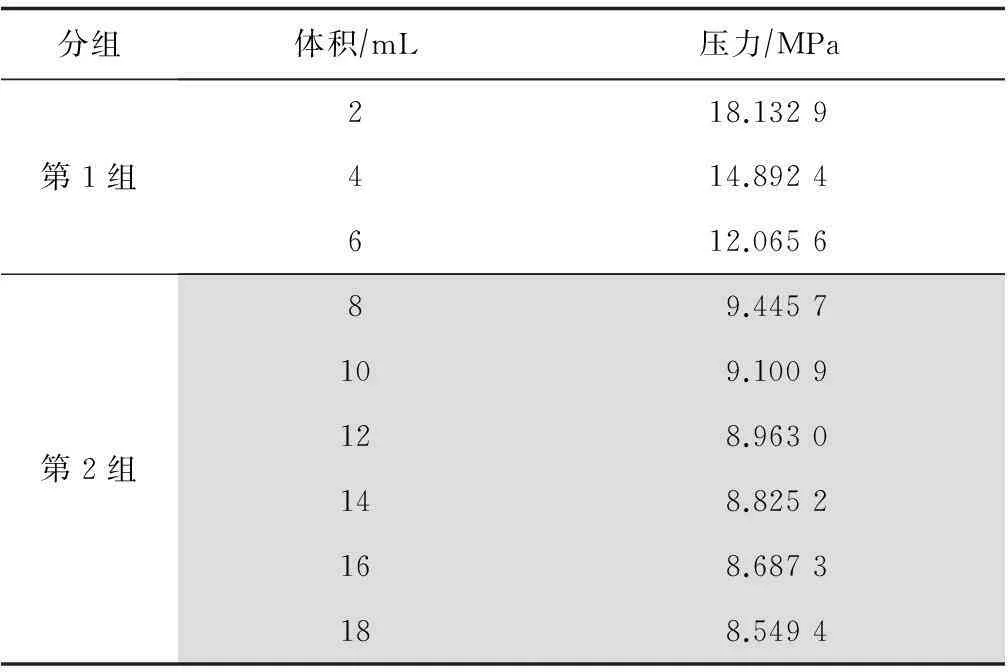
表3　数据点3-6分组

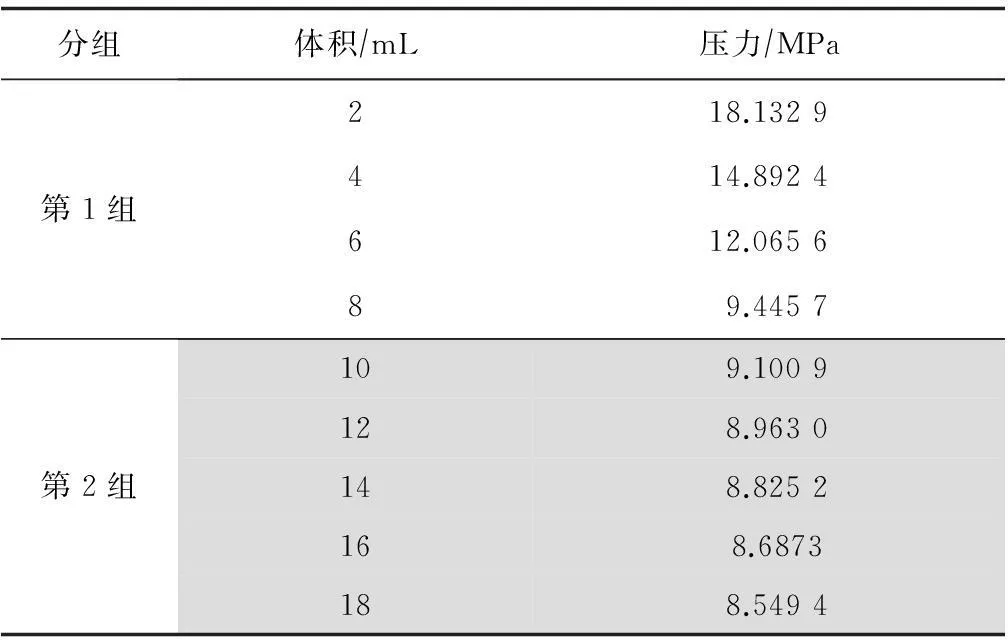
表4　数据点4-5分组

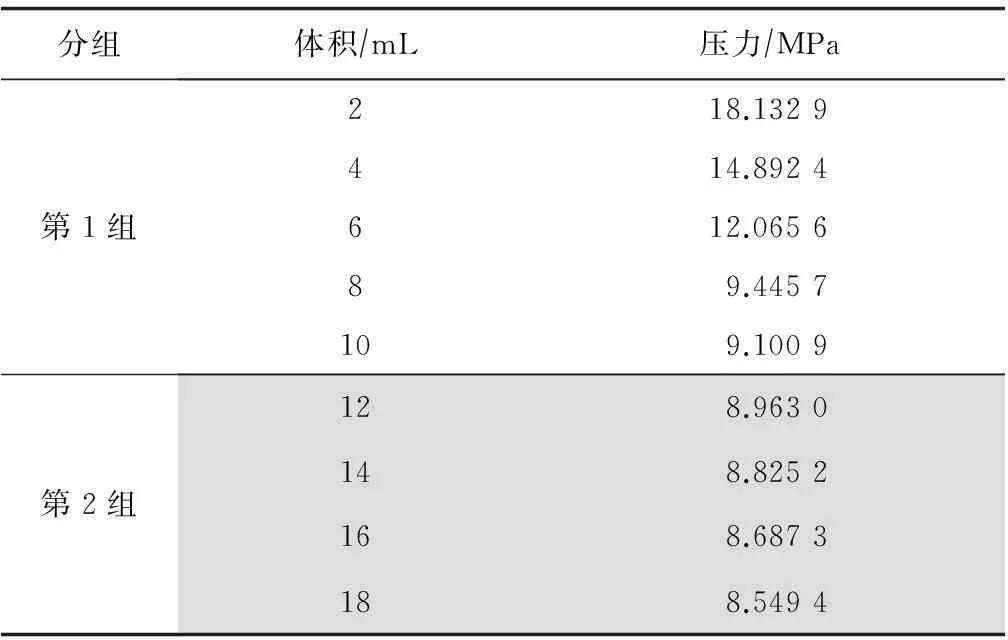
表5　数据点5-4分组

表6　数据点6-3分组

表7　数据点7-2分组

2.2线性回归处理

一元线性回归是描述2个变量之间统计关系的最简单的回归模型[5]，只包括1个自变量和1个因变量。若2个变量数据的散点图呈现出直线趋势时，一般可以通过最小二乘法[6]列出其方程，找到二者的经验公式,经验公式可以大致表达原来函数关系的近似程度。

如果已知数据点(x1,y1)，(x2,y2)，(x3,y3)，…，(xn,yn)在直角坐标系中大致接近于一条直线，可利用线性函数描述为f(x) =ax+b，其中a和b为未知常数。根据公式(1)求取对应的函数值M：

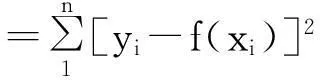
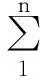
(1)

式中:xi—— 线性函数的自变量；

f(xi) —— 线性函数的因变量;

yi—— 实际数据点的数据。

对二元函数M求偏导数，并令Ma和Mb为0即可，求出未知常数a和b的值，从而确定线性函数f(x) = ax + b ，得到2个变量之间的关系。 每种分组方法的2组数据都可以分别进行线性回归分析。

2.3计算均方误差总和

分别对以上每组数据按照分组情况进行线性回归，求出分组数据的2组均方误差，最后再计算均方误差总和。表8 所示为均方误差数值。

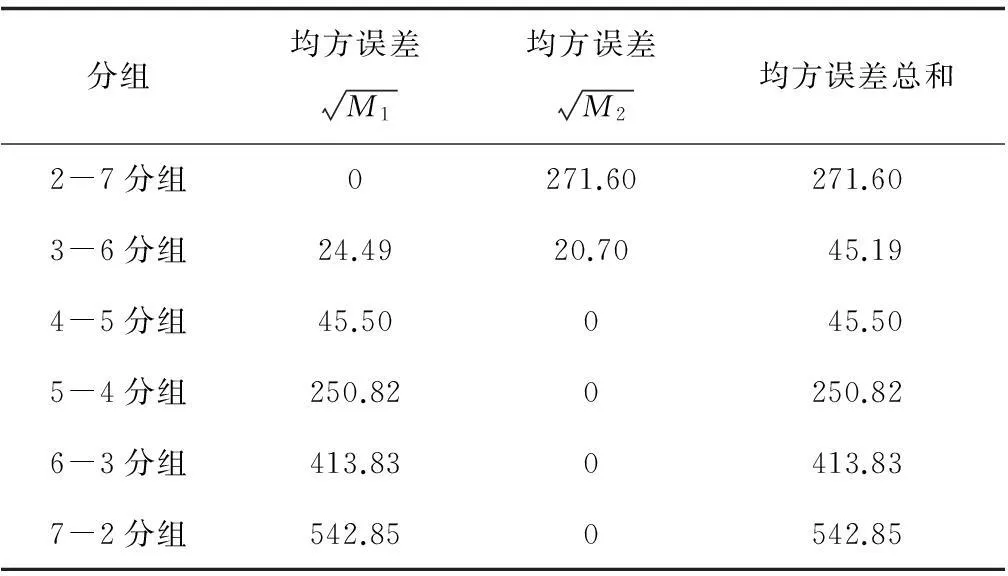
表8　均方误差数值

3-6分组所得的均方误差总和45.19最小，所得到的2条直线(见图2)最能表达函数关系近似程度，这2条直线即为最优直线，这表明3-6分组最为准确。 而人为选点和目测可能会出现4-5分组的情况，结果就不准确。

3程序实现流程

根据以上原理进行编程，具体程序语言不予详述，在此只介绍总体设计实现的流程。

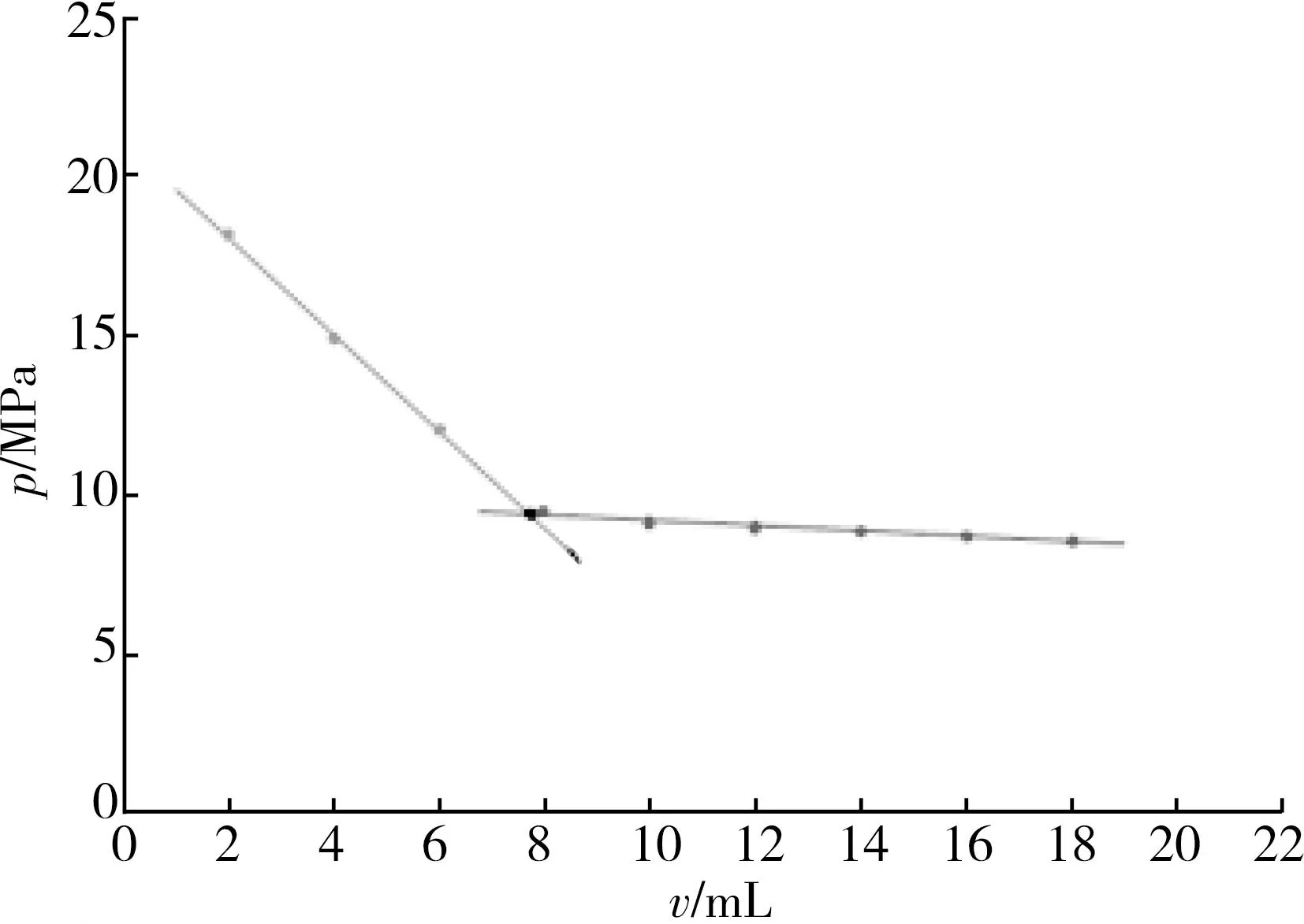
图2　新方法原油p-v关系曲线图

用户在数据输入界面将所有数据依次输入到相应表格中，程序运行后，即直接得到井下PVT样品的泡点压力值和地层原油体积-压力关系曲线。图3所示为总体设计流程图。

图3　总体设计流程图

在经过大量数据测试后，检测泡点曲线图的运行界面，结果显示数据分组均正确，尤其以分组明显的数据作为测试数据时效果最好。

4结语

本次研究所提出的新方法，是一种针对2组数据的优化处理方法，能对数据点准确分组并分别进行线性回归，避免人为目测分组可能产生的误差，保证试油期间求取井下PVT样品的泡点压力值准确可靠。所设计的程序不仅满足了算法准确性的要求，还能快速准确地生成地层原油体积-压力关系曲线，缩短试油期间的高压物性取样现场作业时间。该方法还可以应用于油水界面、气液界面、压力梯度等相关参数的数据处理。

参考文献

[1] 李瑞琪.地层原油高压物性参数预测方法[J].油气田地面工程,2009,28(9)：81-82.

[2] 《勘探监督手册》编写组.勘探监督手册：测试分册[M].北京：石油工业出版社,2013：148-149.

[3] 林炳南,梁昕,赵洪绪.压控式井下单相高压物性取样技术及应用[J].油气井测试,2014,23(3)：61-62.

[4] Proserv UK Ltd.Operations Manual for the Proserv Mark II Model Positive Displacement Sampler Including the Single Phase System [G].2010.

[5] 张敏静,刘雅娜,薛志群.一元线性回归方程有关检验问题的研究[J].价值工程,2012,31(2)：1-2.

[6] 同济大学应用数学系.高等数学[M].北京：高等教育出版社,2002：67-69.

New Method of Calculating Oil Bubble Point Pressure during Well Test

ZHAOHongxu1ZHANGPing2

(1.Sino French Bohai Geoservices Company Limitd, Tianjin 300452, China;2.CNOOC Energy Tech-Drilling and Production Co., Tianjin 300452, China)

Abstract:In order to obtain the accurate reservoir crude oil bubble point pressure, this paper introduced a new method by which we circulated all data point and linear regressing respectively, then calculated sum of mean square error (the least min sum represents the best approximation degree of function relationship).

Key words:oil bubble point; pressure; linear regression; sum of mean square error; well test

收稿日期：2015-09-15

基金项目：国家重大科技专项“高含硫碳酸盐岩气藏气井不停产试井技术”(20111ZX05017-001)

作者简介：赵洪绪(1980 — ),男，满族，吉林九台人，工程师，中法渤海地质服务有限公司，研究方向为试井、生产测井的资料解释。

中图分类号：TE135

文献标识码：A

文章编号：1673-1980(2016)02-0075-04