一种板式电涡流阻尼器的有限元模拟及试验分析

陈政清,黄智文

(湖南大学 风工程与桥梁工程湖南省重点实验室,湖南 长沙　410082)



一种板式电涡流阻尼器的有限元模拟及试验分析

陈政清,黄智文

(湖南大学 风工程与桥梁工程湖南省重点实验室,湖南 长沙410082)

摘要:为了得到一种板式电涡流阻尼器的阻尼特性,文章建立了板式电涡流阻尼器的有限元模型;对不同气隙条件下的阻尼系数和导体板表面的最大磁感应强度进行了分析计算;并在自主开发的振动测试装置上测试了板式电涡流阻尼器的阻尼特性。研究结果表明:有限元计算结果与试验结果吻合较好,根据有限元模拟和振动测试试验可以准确设计和评价板式电涡流阻尼器的阻尼特性。

关键词:振动控制;电涡流阻尼器;电涡流;有限元模拟;永磁体

0引言

电涡流阻尼器是一种利用电涡流的阻尼效应制成的耗能减振装置,具有使用寿命长、维护少和易安装等优点[1]。目前,电涡流阻尼器主要作为调谐质量阻尼器的阻尼元件应用在土木工程结构的振动控制领域。例如,文献[2]研制了一种使用电磁铁作为磁场源的单摆式电涡流调谐质量阻尼器,并采用自由振动试验和强迫振动试验分析其阻尼特性,还把这种单摆式电涡流调谐质量阻尼器用于一个钢框架的振动台模型试验,证明了该装置具有良好的减震效果[3];文献[4]开发了一种使用永磁体作为磁场源的电涡流调谐质量阻尼器,实验表明这种电涡流调谐质量阻尼器比传统的调谐质量阻尼器具有更好的控制鲁棒性;文献[5]从电磁理论出发推导了电涡流阻尼力的理论公式,说明了电涡流调谐质量阻尼器的阻尼特性接近线性黏滞阻尼,同时研究了电涡流调谐质量阻尼器对一个桥梁模型的控制效果,分析表明电涡流调谐质量阻尼器可以精确地调整到最优理论阻尼。然而,上述电涡流调谐质量阻尼器的研究均限于模型试验,并未用于实际土木工程结构的振动控制。

本文开发了一种具有工程实用性的电涡流调谐质量阻尼器,并已用于人行桥的人致振动控制[6]和拱桥刚性吊杆的风致振动控制[7]。在这种电涡流调谐质量阻尼器中,板式电涡流阻尼器作为电涡流阻尼发生装置,对调谐质量阻尼器的性能有着关键影响。本文通过电磁有限元分析和振动试验研究了板式电涡流阻尼器的阻尼特性。

1板式电涡流阻尼器的基本构造

板式电涡流阻尼器的基本构造如图1所示,它由永磁体、永磁体后的铁板、导体板以及导体板后的附加铁板组成。其中,导体板通常选用导电率高的铜板,铁板和附加铁板既起到分别固定永磁体和导体板的作用,又有利于形成闭合磁路、减小系统漏磁、增加铜板内的磁通量。永磁体按照相邻磁体磁极相反的原则布置。

当导体板和永磁体之间发生图1所示的相对运动时,铜板中就会产生电涡流,并受到电磁力的作用。由楞次定理可知,铜板受到的电磁力总是阻碍它和永磁体之间的相对运动。从能量转化的角度看,永磁体或铜板的机械能首先转化为铜板中的电能,并最终转化为热能耗散掉,从而产生阻尼效应。

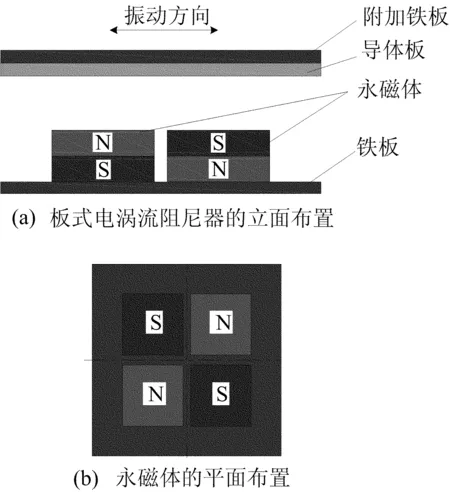
图1　板式电涡流阻尼器的基本构造

影响板式电涡流阻尼器阻尼性能的因素很多,包括永磁体的型号、尺寸和布置方式,导体板的材料和尺寸、气隙的大小以及铁板的材料和尺寸等。尽管已有研究从理论上分析了电涡流阻尼器的阻尼特性,但其研究成果往往只适用于特定的电涡流阻尼器形式。而且,板式电涡流阻尼器中的电磁场具有明显的三维特性,采用简化的理论分析必然带来较大误差,很难满足设计需要。鉴于此,本文将采用振动试验和三维电磁场有限元分析来确定板式电涡流阻尼器的阻尼特性。

2板式电涡流阻尼器的测试试验

2.1试验装置和方法

阻尼测试装置示意图如图2所示。为了测试板式电涡流阻尼器的阻尼特性,把板式电涡流阻尼器安装在图2a所示的振动测试台上。振动测试台为一个强梁弱柱的单层框架,它在水平方向上的自由衰减振动主要为第一阶模态,因此可以看作是一个广义单自由度的振动系统。

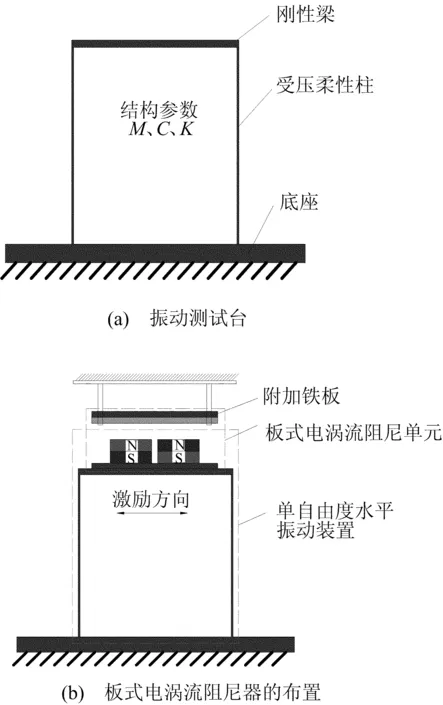
图2　阻尼测试装置示意图

通过比较板式电涡流阻尼器安装前后振动测试台阻尼系数的变化就可以确定板式电涡流阻尼器的阻尼系数Cm,其表达式为:

(1)

其中,Mt为振动系统第一阶水平振动模态的模态质量;ωt和ζt分别为安装板式电涡流阻尼器后结构的固有圆频率和固有阻尼比;C0为板式电涡流阻尼器安装前结构的阻尼系数。

ωt、ζt及C0的值可通过振动测试台的自由衰减振动试验得到。

试验中板式电涡流阻尼器各组成部分的材料参数和尺寸见表1所列,其中气隙表示永磁体与铜板之间的垂直距离,可以通过图2b中的螺旋副调节。

表1　板式电涡流阻尼器的结构参数

2.2试验结果及分析

气隙d在40～80 mm时铜板底面的最大磁感应强度和板式电涡流阻尼器的阻尼系数的变化情况分别如图3和图4所示。

其中最大磁感应强度是通过在铜板底面移动特斯拉计读取到的最大绝对值。为了既能够突出试验数据和有限元计算数据的偏差,又能够更好地反映最大磁感应强度和阻尼系数随气隙变化的规律,图3和图4均同时包含了用线性坐标和对数坐标表示的试验结果。

图3　铜板底面最大磁感应强度与气隙的关系

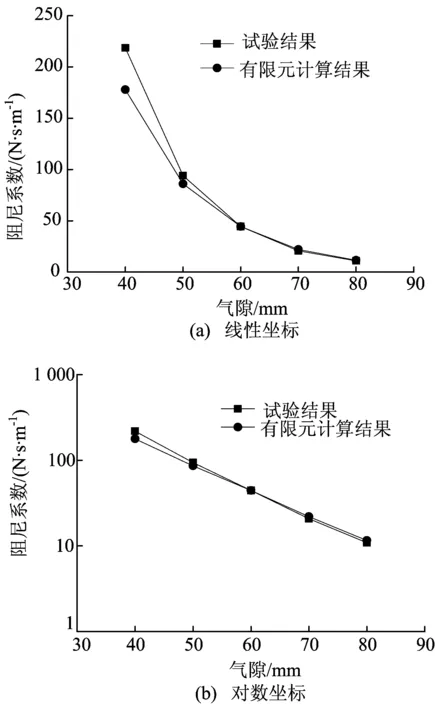
图4　阻尼系数与气隙的关系

由图3和图4可以看出,随着气隙的增加,铜板底部的最大磁感应强度和阻尼系数都呈指数规律衰减。因此,为了尽可能地提高板式电涡流阻尼器的工作效率,在设计时除考虑安装条件和一定的安全距离外,应尽可能地减小气隙大小,提高板式电涡流阻尼器的工作效率。需要说明的是,当气隙d=40 mm时,结构的自由衰减振动只有1个完整的振动周期,此时根据自由衰减振动数据求出的阻尼比和阻尼系数可能存在较大误差。

3板式电涡流阻尼器的有限元模拟

本文采用电磁分析软件Ansoft Maxwell对板式电涡流阻尼器进行三维电磁场有限元分析,其中铜板下表面的最大磁感应强度由稳态磁场分析获得,阻尼系数则由瞬态磁场分析法得到。为了简化计算步骤、节约计算时间,在瞬态磁场分析中并没有完全模拟试验中的磁-固耦合振动现象,而是把永磁体和支撑铁板的运动速度设置为恒定速度v0=0.4 m/s,并计算永磁体和支撑铁板在运动过程中受到的阻力。实际上,已有研究表明当板式电涡流阻尼器的工作速度较小时,其阻尼特性接近线性黏滞阻尼[8],考虑到v0接近试验中板式电涡流阻尼器的最大工作速度,所以其大小并不会影响有限元的计算结果。

3.1导体板内的磁感应强度和电涡流分布

空气间隙d=40 mm时,铜板底面的磁感应强度分布情况如图5所示。由图5可以看出,永磁体投影区域上的磁感应强度要远大于其周边的磁感应强度,而且即使在永磁体的投影范围磁感应强度的平面分布也不均匀,这说明如果在理论分析中采用匀强磁场来代替真实的磁场强度分布,可能会给阻尼系数的计算带来较大误差。

图5　d=40 mm时铜板底面的磁感应强度分布

永磁体运动到铜板正下方时,铜板内的电涡流分布情况如图6所示。由图6可以看出,在永磁体的投影区域有2个明显的旋涡状电涡流,而且相邻永磁体的投影区域上电涡流的方向相反,这是因为相邻磁体的同侧磁极正好相反。

图6　铜板内的电涡流矢量图

3.2最大磁感应强度和阻尼系数

图3和图4分别给出了铜板底部最大磁感应强度和阻尼系数的有限元计算结果,并与试验值进行了比较。比较结果表明,在本文研究的气隙范围内有限元计算的最大磁感应强度与实验结果非常吻合。但对阻尼系数而言,当气隙较大时,有限元计算结果与试验结果吻合较好;而当气隙较小时,有限元计算结果与试验结果偏差较大,其中当d=40 mm时,有限元的计算偏差达到了20%左右。根据第2节末尾的说明可以判断,这种偏差可能是由于阻尼系数的试验值存在误差造成的。从图4b也可以看出,有限元的计算结果比试验结果更加光滑,规律性更好。

4结束语

三维电磁场有限元方法可以准确计算板式电涡流阻尼器的阻尼性能,对板式电涡流阻尼器的设计和优化设计具有重要的指导意义。在板式电涡流阻尼器的设计中应尽量减小气隙的大小,以提高板式电涡流阻尼器的利用效率。

[参考文献]

[1]陈政清，黄智文，王建辉，等.桥梁用 TMD 的基本要求与电涡流 TMD[J].湖南大学学报:自然科学版，2013，40(8):6-10.

[2]方重，吴和霖.电磁涡流耗能调谐质量阻尼器研制与性能试验[J].同济大学学报:自然科学版，2001，29(6):752-756.

[3]楼梦麟，吴和霖，马恒春，等.电磁耗能 TMD 结构减震效率的振动台试验研究[J].地震工程与工程振动，2003，23(4):158-164.

[4]Bae J S，Hwang J H，Roh J H，et al.Vibration suppression of a cantilever beam using magnetically tuned-mass-damper[J].Journal of Sound and Vibration，2012，331(26):5669-5684.

[5]Bourquin F，Caruso G，Peigney M，et al.Magnetically tuned mass dampers for optimal vibration damping of large structures[J].Smart Materials and Structures，2014，23(8):085009-1-85009-13.

[6]Wang Z，Chen Z，Wang J.Feasibility study of a large-scale tuned mass damper with eddy current damping mechanism[J].Earthquake Engineering and Engineering Vibration，2012，11(3):391-401.

[7]汪志昊，陈政清，王建辉.钢拱桥刚性细长吊杆减振用调谐质量阻尼器的试验研究[J].科学技术与工程，2013，13(19):131-136.

[8]Pluk K J W，van Beek T A，Jansen J W，et al.Modeling and measurements on a finite rectangular conducting plate in an eddy current damper[J].IEEE Transactions on Industrial Electronics,2014，61(8):4061-4072.

(责任编辑胡亚敏)

Finite element simulation and experimental test of a plane-type eddy current damper

CHEN Zheng-qing,HUANG Zhi-wen

(Key Laboratory for Wind and Bridge Engineering of Hunan Province,Hunan University,Changsha 410082,China)

Abstract:To obtain the damping characteristic of a plane-type eddy current damper(PECD),a finite element model of the PECD was established.Then the damping coefficient and the maximum flux density on the surface of the conductive plane were computed in regard to different air gaps.Finally,the damping characteristic of the PECD was measured on a self-developed vibration test device.It was shown that the results of finite element simulation agreed well with those of the experiments.Therefore,the damping characteristic of the PECD can be accurately designed and evaluated by using the finite element simulation and the vibration test device.

Key words:vibration control;eddy current damper;eddy current;finite element simulation;permanent magnet

收稿日期：2015-05-31；修回日期：2015-08-18

基金项目：国家自然科学基金资助项目(91215302;51278189)

作者简介：陈政清(1947-),男,湖南湘潭人,博士,湖南大学教授,博士生导师.

doi:10.3969/j.issn.1003-5060.2016.04.014

中图分类号:TB535.1

文献标识码：A

文章编号：1003-5060(2016)04-0499-04