强化现象启发的随机振动能量收集器优化设计

田燕萍,金肖玲,王　永

(1.杭州电子科技大学 机械工程学院,浙江 杭州 310018；2. 浙江大学 工程力学系,浙江 杭州 310027)



强化现象启发的随机振动能量收集器优化设计

田燕萍1,金肖玲2,王永2

(1.杭州电子科技大学 机械工程学院,浙江 杭州 310018；2. 浙江大学 工程力学系,浙江 杭州 310027)

摘要:为了使宽带振动能量收集器件的平均输出功率最大,以压电型随机振动能量收集器件为研究对象,系统讨论优化设计问题.通过建立器件随机响应与输出功率统计量的解析表达式,证实了平均输出功率的局部强化现象.讨论给定激励点位置时,压电片布置位置和压电片尺寸的优化,讨论最优尺寸随激励作用点和激励带宽的变化关系.研究表明：激励作用点及对称位置是布置压电片的较好位置,压电片的最优、次优、最差、次差位置相隔很近；为了得到最大的输出功率,压电片尺寸应略大于最优尺寸.

关键词：随机振动；能量收集器；优化设计；输出功率均值

随着微电子器件功耗的下降及其制造工艺的迅速发展,振动能量收集技术受到科学界及产业界的广泛关注[1-3].该技术的发展可延长功能器件的电池寿命,甚至完全取代电池,构成能源自给的自供电功能器件.在难以更换电池或更换风险较大的场合,例如分布式传感系统及植入式电子医疗器件等领域,极具前景.

压电式振动能量收集器件是最广泛被采用的一种能量转化器件,其中最典型且研究最多的为一维梁型结构[3-4].最近,Aridogan等[5-6]发展了基于平板结构的压电式能量收集器件.压电式振动能量收集器件的早期研究均是基于共振原理进行的,几乎完全集中于谐和激励情形[7-8],并对压电片形状、尺寸进行了优化设计[9-12].由于环境振动本质上是随机的,振动能量分布于一定的带宽之内,为更好地应用振动能量收集技术,应全面研究随机方面[2,13].

随机激励作用下振动能量收集器件的研究大都针对由单自由度机械系统[3].对于仅包含器件基频的窄带激励,所得结果是近似正确的,但对于包含多个模态的宽带激励,所得结果本质上是错误的,它没有能计及高阶模态的影响[14].最近,Aridogan等[6]、Zhao等[15]针对一维梁型及二维平板型能量收集器件,从分布参数模型出发建立了电压及逐点位移对激励的频率响应函数,并据此给出白噪声作用下输出功率分析的预测方法.由于连续型能量采集技术的研究刚刚起步,对白噪声激励下压电振动能量收集器件的优化设计工作,尚有大量问题需要解决.本文延续上述研究,从连续体随机振动理论中局部强化现象出发,全面讨论梁型振动能量收集器件在白噪声激励下的优化设计问题.

1模型描述与理论分析

1.1压电型随机振动能量收集器件的物理描述及数学建模

压电层本构方程[16]为

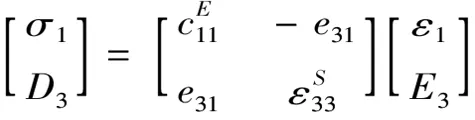
(1)

图1　压电型振动能量收集系统示意图Fig.1　Schematic of piezoelectric-type vibration energy harvesting system

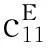
(2)

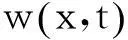
根据方程(1)和(2)推导可得关于中面横向位移的控制方程：

(3)式中:I=bh3/12为母梁的惯性矩,θ=e31b(h+hp)/2为机电耦合系数,v 为施加于外电阻R的电压,且 v=-E3hp.由于压电层厚度较母梁厚度要小得多,因此推导中忽略了压电层刚度对弯矩的贡献.

电路系统由控制方程描述[7]为

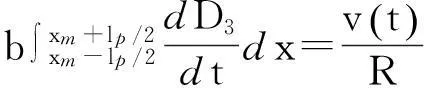
(4)

将压电本构方程及几何方程代入整理得

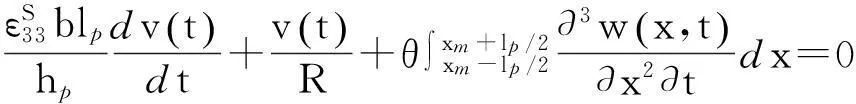
(5)

方程(3)和(5)即为描述梁型振动能量收集系统的完整微分方程组,二者相互耦合.

为使之后的优化结果具有普适性,首先导出相应的无量纲控制方程组为

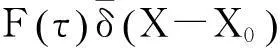
(6)

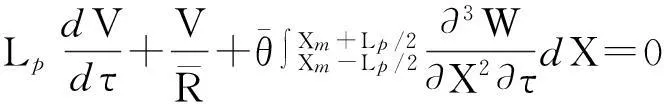
(7)

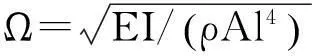
(8)

式中:p1=v2/R 为有量纲的系统输出功率.

1.2随机响应及平均输出功率预测

无量纲控制方程组(6)和(7)对系统激励性质没有限制,对于随机激励情形,该微分方程组为随机微分方程组,所有导数运算都在均方意义下进行[17].考虑到激励由单一随机过程描述,根据线性随机振动理论,对给定位置的横向位移及输出电压进行讨论时,均可视系统为单输入单输出系统.因此,需首先确定系统的频率响应函数,即在周期激励作用下系统的幅值和频率响应特性.

应用模态分析法,横向位移可表示为

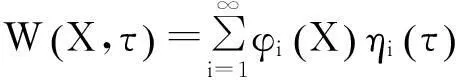
(9)

应用Galerkin方法,将式(9)代入系统方程(6)并乘以模态函数积分,得到关于模态响应函数的常微分方程组：

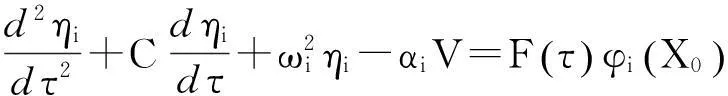
(10)

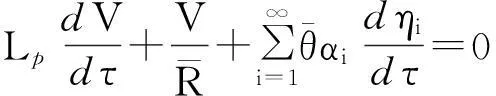
(11)

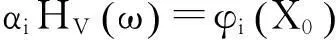
(12)

(13)

联立式(12)、(13)得到[15]

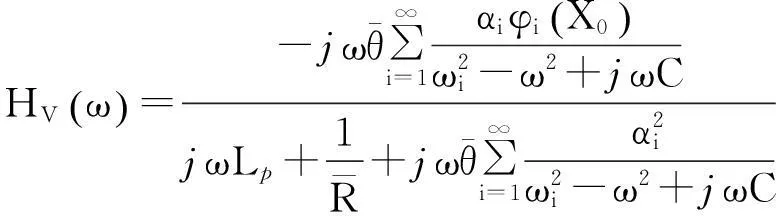
(14)

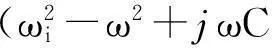
(15)

横向位移的频率响应函数由模态频率响应函数表示为

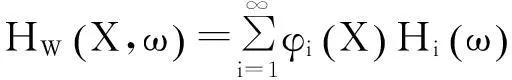
(16)

(17)

(18)

母梁的曲率均方值表示为

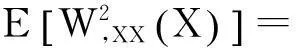
(19)

(20)

输出功率的均值为

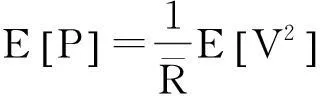
(21)

式(17)～(21)可用于预测任意平稳随机激励作用下的稳态响应统计量.为了研究的确定性,本文限定激励为限带白噪声过程,其功率谱密度分段表示为

(22)

式中:S0为常数.对限带白噪声激励,各响应统计量公式中的无穷积分限可改为有限积分限[-ω0,ω0],且可将功率谱密度S0从积分号中提出.上述各响应统计量均与S0成正比,因此在以下分析中所有统计量均用S0做了归一化.

2局部强化现象的证实

线性随机振动理论的研究表明,纯弹性结构中存在奇异的局部强化现象,即速度均方值在某些特定位置出现极大的强化[17].有理由猜测其他特征响应,如曲率等的响应均方值亦会存在类似的局部强化现象.本节将首先验证纯弹性结构中曲率均方值的局部强化现象,并讨论小尺寸压电片对纯弹性母结构曲率强化现象的影响；进而证实压电片布置位置变化时,输出功率均值的强化现象.

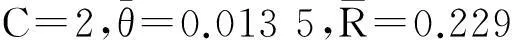
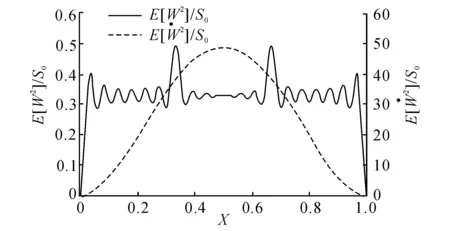
图2　位移和速度响应均方值沿母梁轴线分布图Fig.2　Variation of mean-square displacement and mean-square velocity along axis of beam

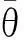
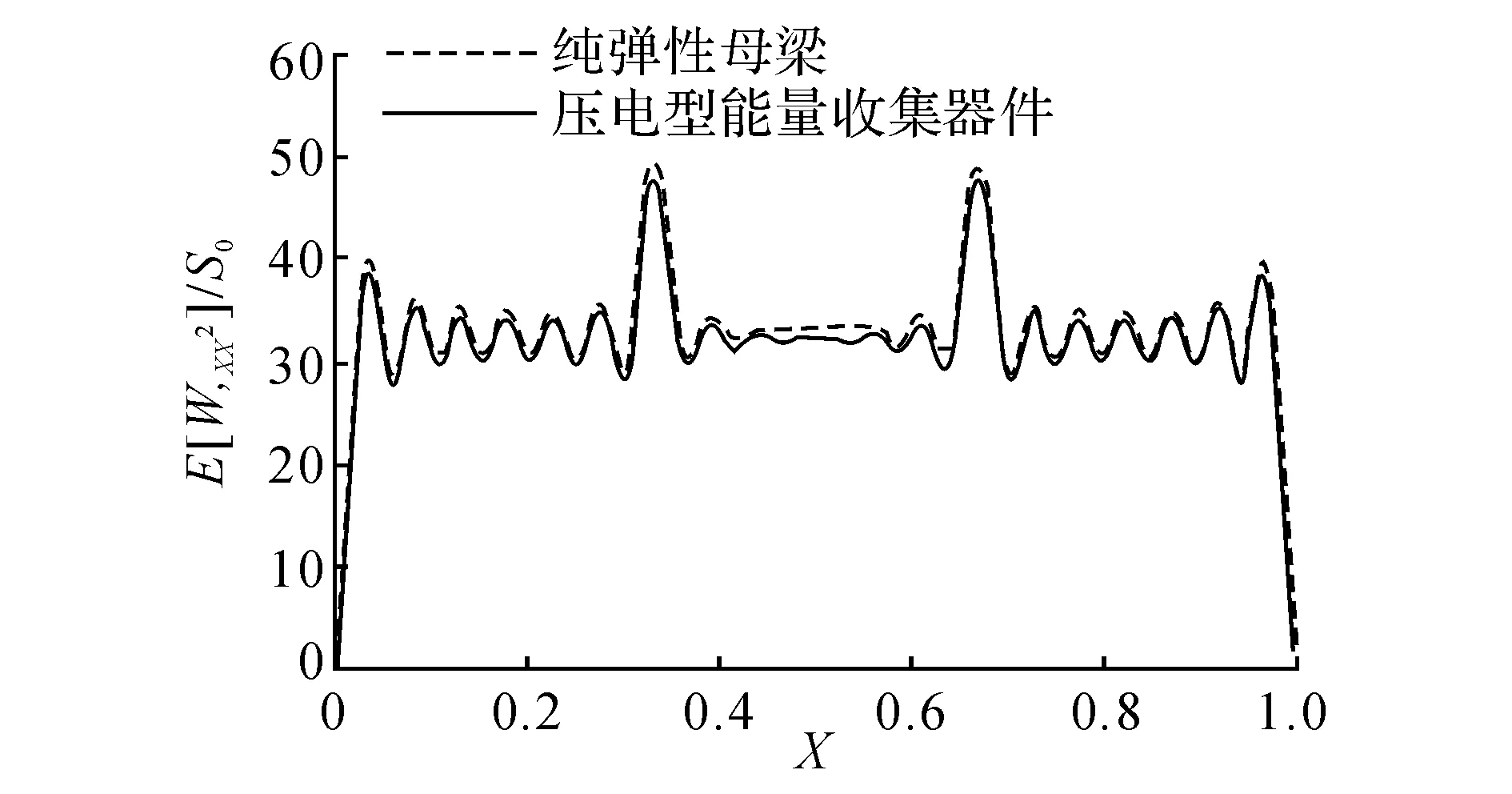
图3　曲率均方值沿母梁轴线分布图Fig.3　Variation of mean-square curvature along axis of beam

压电型能量收集器件通过母结构变形引起压电材料变形实现能量收集,因此若布置压电层于曲率强化峰值处,必将显著提高收集功率.然而,压电层通过机电耦合效应影响母结构的动态行为,因此需首先研究小尺寸压电片对纯弹性母结构曲率强化现象的影响.取X0=1/3,ω0=4 000,Xm=1/3,Lp=0.01,压电型能量收集器件的母结构曲率均方值沿轴线分布如图3中实线所示,由图3可见,小压电片的存在对母结构曲率均方值的影响很小,数值上略微变化且仍近似对称.因此,通过曲率强化现象指导压电型能量收集器件的优化设计是合理的.

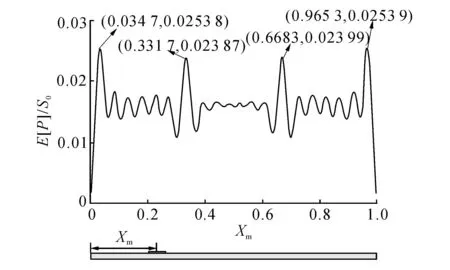
图4　压电层中心位置移动时,输出功率均值的强化现象Fig.4　Local strengthening phenomenon of mean output power with moving of piezoelectric patch center

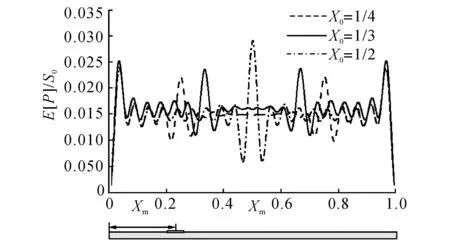
图5　平均输出功率随压电片中心位置变化的强化现象Fig.5　Local strengthening phenomenon of mean output power with moving of piezoelectric patch center

取X0=1/3,ω0=4 000,Lp=0.01,压电片中心位置从梁端移动到梁尾过程中,其平均输出功率的变化如图4所示.由图4可见,平均输出功率亦出现局部强化现象,且相对于简支结构中心位置具有近似对称性.其强化位置与图3中曲率均方值的强化位置一一对应,这是由于输出电压与母梁曲率的直接相关性.由于复杂的机电耦合行为,2种强化现象中最大及次大的强化峰发生了切换.取ω0=4 000, Lp=0.01,如图5所示给出了激励作用于不同位置(X0=1/4,1/3,1/2)时,平均输出功率随压电片位置的变化关系.结果表明：无论激励作用于何处,平均功率均有强化现象出现.注意到平均功率的近似对称性,在以下分析中,该强化现象均按对称处理.图5亦体现了平均功率强化现象的剧烈变化特征,即极大和极小平均功率交替出现.这表明,为得到最大的输出功率,需谨慎选择压电片的中心位置.

3压电片位置优化

如图6和7所示分别为X0=1/2,Lp=0.01时,随激励带宽变化压电片最优、次优、最差及次差位置的变化及相应的平均输出功率.由图6、7可知,对于任意的激励带宽,压电片最优位置处于母梁中心,即激励作用点位置.当激励带宽增大时,压电片次优位置向梁端偏移,并最终处于某稳定位置.压电片最差位置及次差位置分别紧邻最优及次优位置,最优位置与次优位置的输出功率偏差不是非常显著.当压电片分别布置于最优位置和最差位置时,平均输出功率有相当大的差别.例如,当外激励的上截止频率为 ω0=4 000,压电片处于最优位置X0=0.5的平均输出功率为3.808×10-2,处于最差位置X0=0.470的平均输出功率为8.522×10-3,即最优平均输出功率是最差平均输出功率的4.47倍.

图6　激励带宽对压电片最优、次优、最差及次差布置位置的影响Fig.6　Effect of excitation bandwidth on optimal, sub-optimal, worst and sub-worst locations of piezoelectric patch

图7　激励带宽对最优、次优、最差及次差功率均值的影响Fig.7　Effect of excitation bandwidth on optimal, sub- optimal, worst and sub-worst mean output power

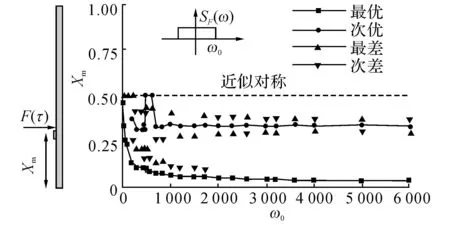
图8　激励带宽对压电片最优、次优、最差及次差布置位置的影响Fig.8　Effect of excitation bandwidth on optimal, sub- optimal, worst and sub-worst locations of piezoelectric patch

如图8和9所示分别给出了X0=1/3, Lp=0.01时,压电片最优、次优、最差及次差位置以及相应的各平均输出功率.由图8、9可见,随着激励带宽的增大,最优位置迅速向梁端偏移,次优位置发生剧烈波动后稳定在激励作用点附近；最差及次差位置在带宽较小时十分混乱,而带宽较大时稳定在次优位置附近,尽管有显著跳跃现象发生.最优及次优平均输出功率值接近,最差及次差平均输出功率值接近,2组值相差约一倍.为进一步总结规律,如图10和11所示给出了X0=1/4,Lp=0.01时的情形.由图10、11可知,当激励带宽较小时,最优、次优、最差及次差位置没有规律可言；当激励带宽较大时,最优及次优位置分别位于梁端及激励作用点附近,最差及次差位置位于次优位置两侧.

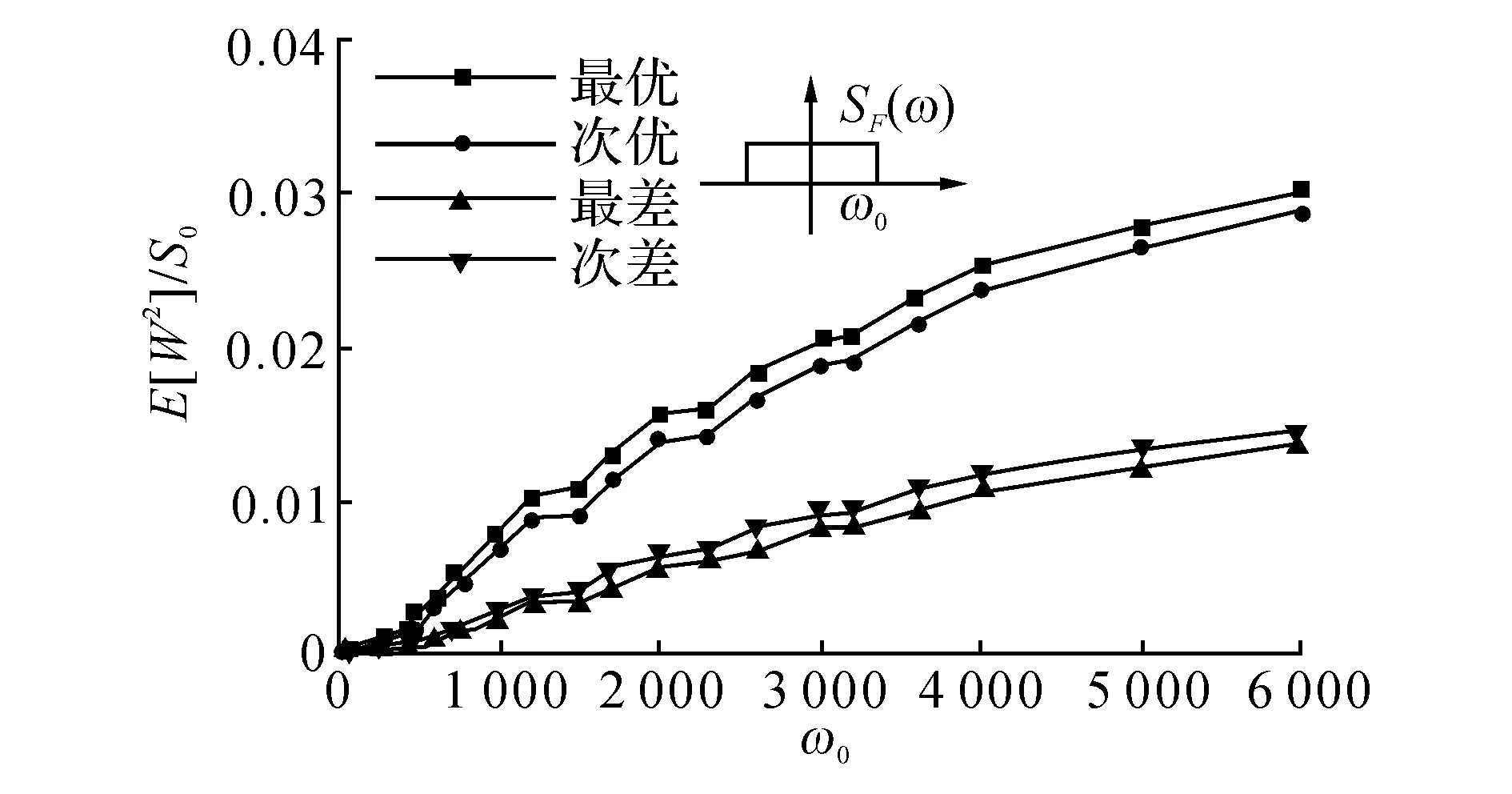
图9　激励带宽对最优、次优、最差及次差功率均值的影响Fig.9　Effect of excitation bandwidth on optimal, sub- optimal, worst and sub-worst mean output power

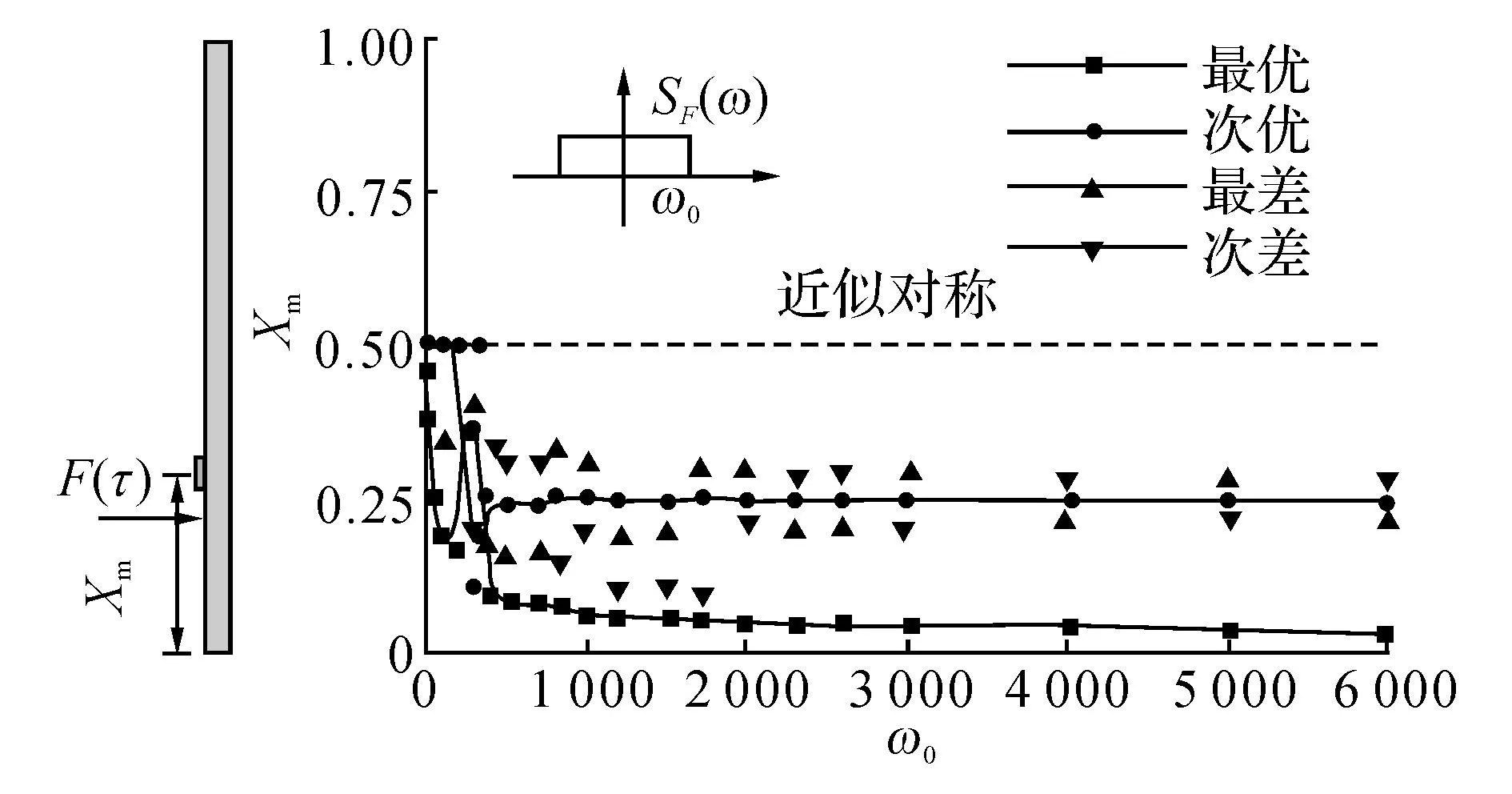
图10　激励带宽对压电片最优、次优、最差及次差布置位置的影响Fig.10　Effect of excitation bandwidth on optimal, sub- optimal, worst and sub-worst locations of piezoelectric patch

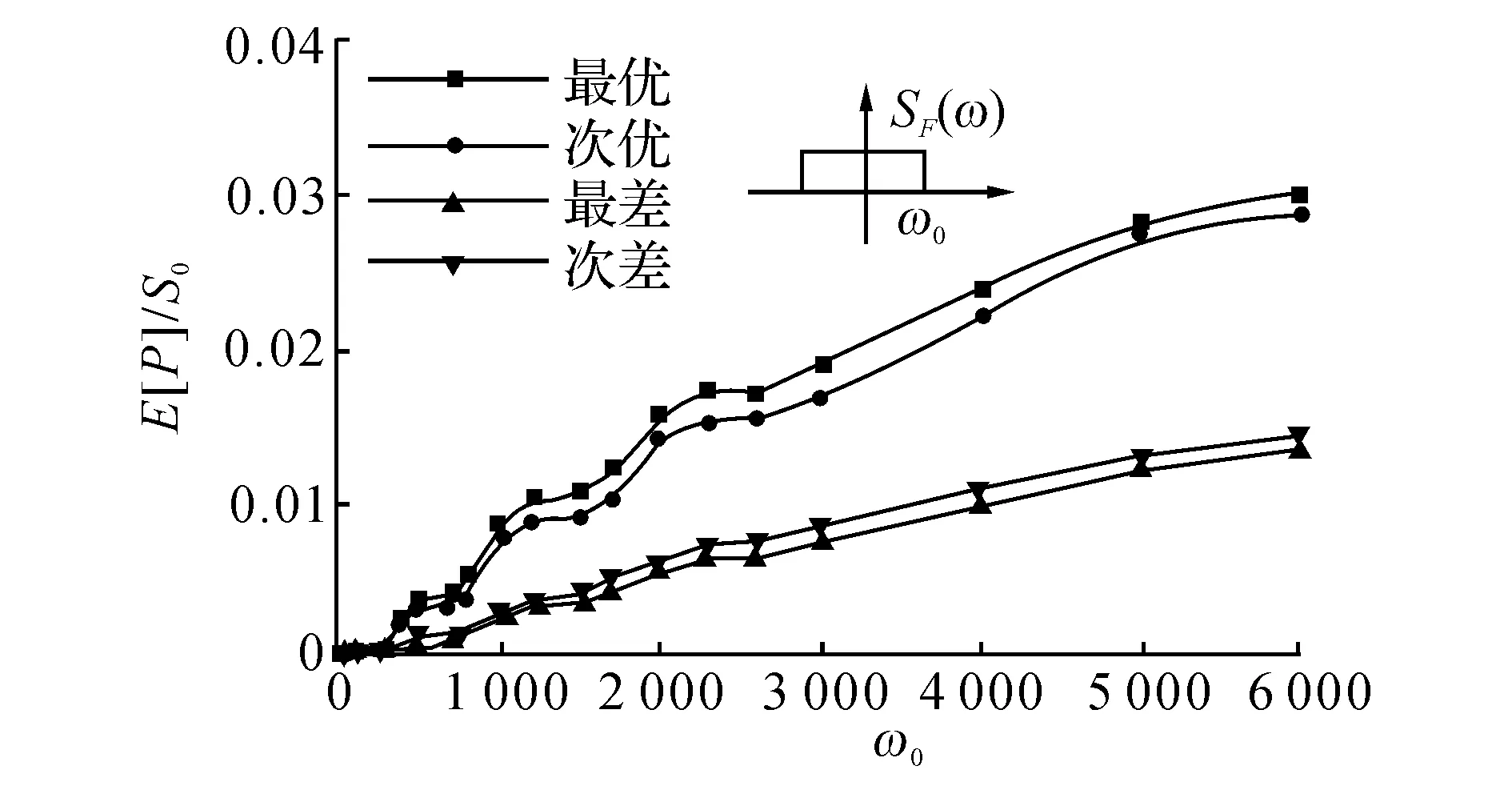
图11　激励带宽对最优、次优、最差及次差功率均值的影响Fig.11　Effect of excitation bandwidth on optimal, sub- optimal, worst and sub-worst mean output power

对上述3种典型情况的讨论说明,当激励带宽较小时,最优、次优、最差及次差位置没有明显规律可言,这是由于带宽较小时局部强化现象不明显；当激励带宽较大时,最优及次优两位置位于激励作用点及梁端附近,而最差及次差两位置紧邻最优及次优两位置.因此,激励带宽较大的情形对宽带能量收集更有意义.又注意到最优及次优位置的平均输出功率并没有明显偏差,因此在后文关于压电片最优尺寸的讨论中均保持压电片与激励点处于同一位置.

4压电片尺寸优化

太小的压电片尺寸产生过少的电荷,而过大的压电片尺寸将覆盖应变的正负交替区域,即越过应变节点,从而引起电荷相消[11],这些对于能量收集都是非常不利的.存在最优的压电片尺寸,使得平均输出功率达到最大值.如图12所示给出了ω0=4 000下,平均输出功率随压电片尺寸的变化关系,由图12可见,对于典型的3种激励作用及压电片布置位置,确实都有最优的压电片尺寸.压电片小于最优尺寸时输出功率剧烈下降,因此应使得压电片尺寸不小于最优尺寸以期获得较大平均输出功率.如图13所示给出了压电片最优尺寸随着激励作用点位置,也即压电片中心位置的变化关系.由图13可见,随着激励作用点位置的移动,压电片最优尺寸发生波动；且总体而言,越大的激励带宽相应于越小的压电片最优尺寸.从实用角度讲,对给定的激励带宽,压电片尺寸可取最优尺寸的最大值,这是由于若压电片尺寸小于最优尺寸则将导致输出功率的急速下降(如图12所示).如图14所示给出了压电片最优尺寸随激励带宽的变化关系.由图14可知随着激励带宽的增加,压电片最优尺寸显著减小.且压电片最优尺寸对激励作用点位置,即压电片中心位置不太敏感.

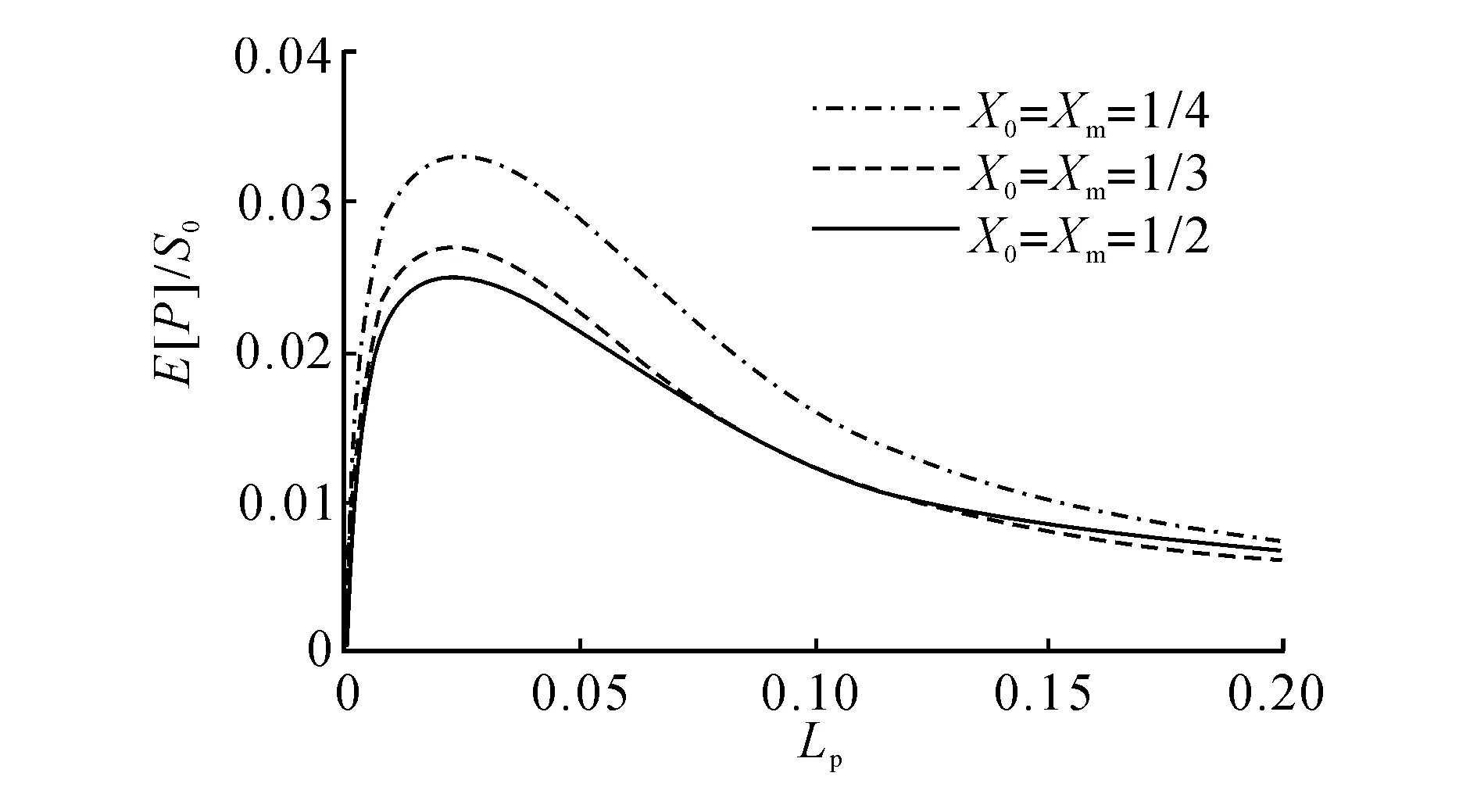
图12　平均输出功率随压电片尺寸的变化Fig.12　Mean output power vs. size of piezoelectric patch

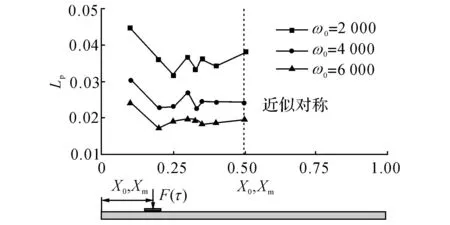
图13　压电片最优尺寸随激励作用点(压电片中心)位置的变化Fig.13　Optimal size of piezoelectric patch vs. excitation location, i.e., piezoelectric patch center

图14　压电片最优尺寸随激励带宽的变化Fig.14　Optimal size of piezoelectric patch vs. excitation bandwidth

5结论

在线性随机振动理论局部强化现象的启发下,本文系统研究了压电型随机振动能量收集器件的优化设计问题.主要结论如下：

(1)对于给定的激励带宽和激励点位置,压电片最优及次优两位置分别处于梁端附近及激励作用点附近,且最差和次差位置分别临近上述两较优位置,这要求压电片的中心位置需谨慎选择.

(2)激励作用点及激励作用点的中心对称位置一定是最优位置或次优位置,而激励作用点可能不适合布置压电片,因此,直接布置压电片于激励作用点的中心对称位置就成为最好选择.

(3)当压电片尺寸小于最优尺寸时,平均输出功率将急剧下降,因此应选择压电片尺寸略大于最优尺寸,从而提高鲁棒性,应对外界环境的不确定变化.

(4)若外界激励不具有固定带宽,需考察哪个带宽占据主导地位,并据此给出最优尺寸.

参考文献(References):

[1] BEEBY S P, TUDOR M J, WHITE N M. Energy harvesting vibration sources for microsystems applications [J]. Measurement Science and Technology, 2006, 17(12): R175-R195．

[2] TANG L, YANG Y, SOH C K. Toward broadband vibration-based energy harvesting [J]. Journal of Intelligent Material Systems and Structures, 2010, 21(18): 1867-1897．

[3] DAQAH M F, MASANA R, ERTURK A, et al. On the role of nonlinearities in vibratory energy harvesting: a critical review and discussion [J]. Applied Mechanics Reviews, 2014, 66(4): 040801．

[4] ANTON S R, SODANO H A. A review of power harvesting using piezoelectric materials (2003-2006) [J]. Smart Materials and Structures, 2007, 16(3): R1-R21．

[5] ARIDOGAN U, BASDOGAN I, ERTURK A. Analytical modeling and experimental validation of a structurally

integrated piezoelectric energy harvester on a thin plate [J]. Smart Materials and Structures, 2014, 23(4): 045039．

[6] ARIDOGAN U, BASDOGAN I, ERTURK A. Multiple patch-based broadband piezoelectric energy harvesting on plate-based structures [J]. Journal of Intelligent Material Systems and Structures, 2014, 25(14): 1664-1680．

[7] ERTURK A, INMAN D J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations [J]. Smart Materials and Structures, 2009, 18(2): 025009．

[8] ERTURK A, TARAZAGA P A, FARMER J R,et al. Effects of strain nodes and electrode configuration on piezoelectric energy harvesting from cantilevered beams [J]. Journal of Vibration and Acoustics, 2009, 131(1): 011010．

[9] RUPP C J, EVGRAFOV A, MAUTE K, et al. Design of piezoelectric energy harvesting systems: a topology optimization approach based on multilayer plates and shells [J]. Journal of Intelligent Material Systems and Structures, 2009, 20(16): 1923-1939．

[10] FRISWELL M I, ADHIKARI S. Sensor shape design for piezoelectric cantilever beams to harvest vibration energy [J]. Journal of Applied Physics, 2010, 108(1): 014901．

[11] WICKENHEISER A M. Design optimization of linear and nonlinear cantilevered energy harvesters for broadband vibration [J]. Journal of Intelligent Material Systems and Structures, 2011, 22(11): 1213-1225．

[12] WANG Q, WU N. Optimal design of a piezoelectric coupled beam for power harvesting [J]. Smart Materials and Structures, 2012, 21(8): 085013.

[13] ZHU D, TUDOR M J, BEEBY S P. Strategies for increasing the operating frequency range of vibration energy harvesters: a review [J]. Measurement Science and Technology, 2010: 21(2): 022001．

[14] WICKENHEISER A M. Model reduction in stochastic vibration energy harvesting using compressive sampling [J]. Smart Materials and Structures, 2013, 22(9): 094029．

[15] ZHAO S, ERTURK A. Electroelastic modeling and experimental validations of piezoelectric energy harvesting from broadband random vibration of cantilevered bimorphs [J]. Smart Materials and Structures, 2013, 22: 015002．

[16] YANG J S. The Mechanics of Piezoelectric Structures [M]. New York: World Scientific, 2006: 22-34．

[17] 朱位秋. 随机振动[M].北京:科学出版社,1994:179-201．

Strengthening phenomenon-inspirited optimum design ofrandom vibration energy harvester

TIAN Yan-ping1, JIN Xiao-ling2, WANG Yong2

(1.SchoolofMechanicalEngineering,HangzhouDianziUniversity,Hangzhou310018,China;2.DepartmentofEngineeringMechanics,ZhejiangUniversity,Hangzhou310027,China)

Abstract:The optimum design of piezoelectric-type random vibration energy harvester was investigated to acquire the maximum mean output power. The analytical formula for the statistics of random responses and output power were established. Then the local strengthening phenomenon of mean output power were verified. For given excitation locations, the optimal locations and optimal length of piezoelectric patch were derived, and the relations of the optimal length to the excitation location and excitation bandwidth were discussed. Results show that the excitation and its symmetry location are good places for piezoelectric patch. The optimal, sub-optimal, worst and sub-worst locations of piezoelectric patch are very close. The length of piezoelectric patch should be slightly larger than the optimal design value in order to obtain the maximum output power．

Key words:Random vibration; energy harvester; optimum design; mean output power

收稿日期：2015-05-23.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(11302064, 11472240, 1153000141, 51405118);中央高校基本科研业务费(2016FZA4025).

作者简介：田燕萍(1983- )，女，讲师，从事结构动力学、智能材料与结构的等研究. ORCID: 0000-0003-1684-9749. E-mail: tianyanp@sina.cn通信联系人：王永，男，副教授.ORCID: 0000-0002-9741-3367. E-mail: ypwang@zju.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.05.017

中图分类号：O 324

文献标志码：A

文章编号：1008-973X(2016)05-0934-07