基于单点变异算法的单元分组问题的研究

韩　毅,王德志,林华珍,顾　冰

(1.浙江工业大学 经贸管理学院，浙江 杭州 310023;2.浙江工业大学 浙江省技术创新与企业国际化研究中心，浙江 杭州 310023)



基于单点变异算法的单元分组问题的研究

韩毅1,2,王德志1,林华珍1,顾冰1

(1.浙江工业大学 经贸管理学院，浙江 杭州 310023;2.浙江工业大学 浙江省技术创新与企业国际化研究中心，浙江 杭州 310023)

摘要：针对单元制造中单元构建问题所涉及到的单元分组数问题，结合零件—设备关联矩阵的特点，提出一种划分单元数的新颖算法.以直接聚类算法(DCA)的计算结果为基础，根据4种不同的扩张路径形成决策序列.对决策序列进行单点变异，利用单元成组效率评价指标对决策序列进行评价.算例结果表明：对于复杂的初始关联矩阵,所提算法可以提高单元划分的成组效率，得到较满意的结果.

关键词：单元制造系统；直接聚类算法；单元分组数；单元构建

当前，国家发布了《中国制造2025》行动纲领，全面部署推进实施制造强国战略，力图打造一批具有国际竞争力的制造业，从而把我国建设成为引领世界制造业发展的制造强国.单元生产是根据加工零件的工艺路线的相似性形成零件簇，从而利用机器设备对零件簇进行生产加工的一种先进生产方式，具有订单响应时间短、成品库存少和生产成本低等多方面的优点[1]，从80年代成功运用之后，就受到国内外学者和企业界越来越多的关注与重视.Wang等[2]通过采用分散搜索算法解决了多目标动态单元构建问题；金晶等[3]等以物流量最少和机床负荷均衡为目标，采用遗传算法验证了模型的有效性；针对单元制造中异常零件最少与设备利用率最高的问题，Jamal等[4]根据问题的规模，提出了2种不同的解决方案；余世根等[5]利用遗传算法对多目标情况下具有固定约束条件的制造车间的布局问题进行研究；而马玉敏等[6]通过对传统遗传算法进行改进，提高了算法求解同一问题的效率.范佳静等[7]等考虑了总搬运成本及机器设备的维修和折旧成本为目标，利用改进的遗传算法对数学模型进行求解.Rafiei等[8]和Niakan等[9]讨论了操作者在单元生产中的作用，以此实现企业利益和社会责任的平衡.

但是以上研究中，针对单元制造中单元构建问题所涉及到的单元分组数，大多数情况都是学者根据经验判断事先给定.单独针对单元分组数的相关研究文献还比较少.Zahir等[10]根据加工费用和零件搬运距离为目标，以获得最佳单元数；陈形丰等[11]研究了在多品种少批量下的离散型制造企业车间布局分布问题；王建维[12]利用4个经典的聚类有效性函数作为综合性能指标，选择最佳单元分组数，从而避免单一指标做出误判的情形.张传忠等[13]等通过对直接聚类算法进行改进，直接对零件—设备关联矩阵进行操作，从而确定单元分组数.针对单元分组数问题，将在直接聚类算法求解结果的基础上，根据矩阵自身的特点提出4种不同的扩张路径，从而形成不同的决策序列，对每一种决策序列进行变异和评价，从而确定最佳单元分组数.

1单元构建问题描述与直接聚类算法(DCA)

1.1问题描述

单元构建主要是通过对零件进行工艺分析，将所加工零件和机器设备进行分组，从而形成特定的零件簇和设备组，构成一个独立的制造单元.在形成制造单元的过程中，某些零件需要进行跨单元加工，这导致生产单元不能独立进行管理.因此，合理进行单元划分减少跨单元件的数量成为单元构建问题最重要的目标函数之一.而单元分组数作为单元构建问题的重要参数之一，如何进行优化以获取最优单元分组数至今尚没有一致性的方法.

1.2直接聚类算法(DCA)

基于矩阵的簇聚法是解决制造单元划分问题中最常用的方法之一.该方法主要利用表1所示的零件—设备关联矩阵，矩阵中元素“1”表明零件需要相应设备的加工，否则为空格.将零件作为行、设备作为列填入到矩阵中，通过对该初始矩阵按照一定的规则进行行列置换，最终将相似零件和对应加工机器设备聚集在一起，形成一组具有较高密度“1”的对角块矩阵.其中每一个子矩阵就代表一个制造单元.Chan等[14]提出的直接聚类算法就是将行列交错移位，在矩阵的左上角形成簇聚组.

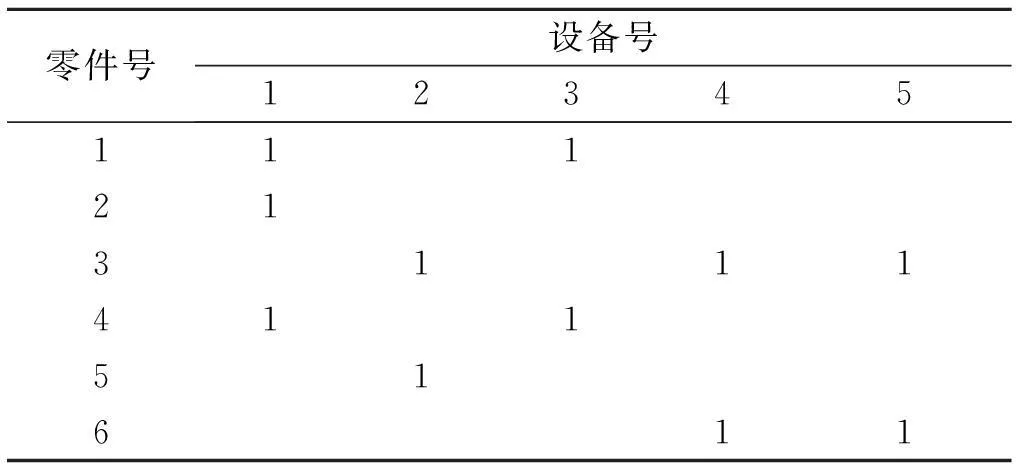
表1　零件—设备关联矩阵

直接聚类算法根据对初始矩阵的零件行和设备列进行置换，最终形成由元素“1”组成的集中块，如表2所示.其具体算法步骤如下：

步骤1对行、列进行排序.将初始矩阵的每行、每列的元素“1”相加.其中以行总和递减的方式从上到下排列，各列以列总和递增的方式从左到右排列.如果行或列总和相同，再以零件号或设备号递减方式排列.

步骤2列移动.将第一行有元素“1”的各列移到矩阵的左边，对剩余各行重复上述过程，直到不能再移动.

步骤3行移动.将第一列有元素“1”的各行向上移动，尽可能组成由“1”组成的集中块.对剩余各列重复上述过程.

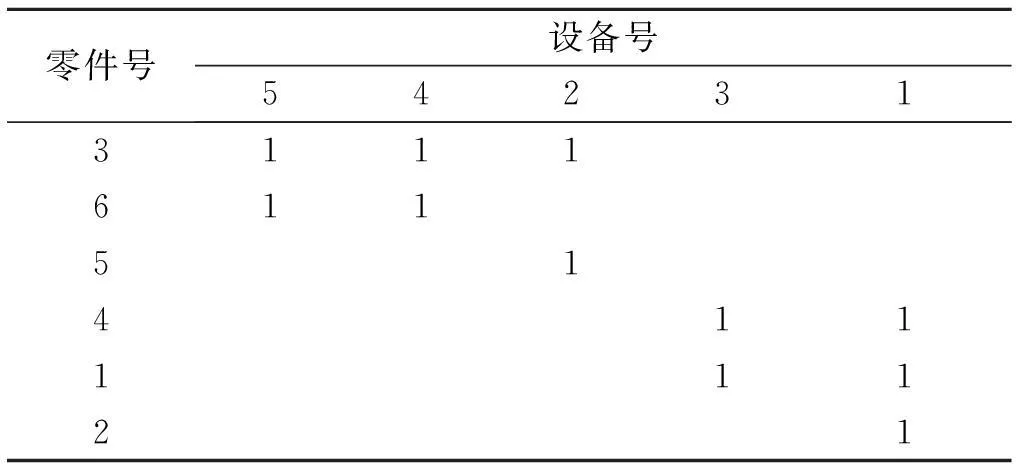
表2　行和列调整后的矩阵

在表2所形成的对角矩阵块的基础上，制造企业可以根据自身实际情况自由组合，将设备和零件进行不同划分，从而形成多种目标效果不同的制造单元，如图1所示.

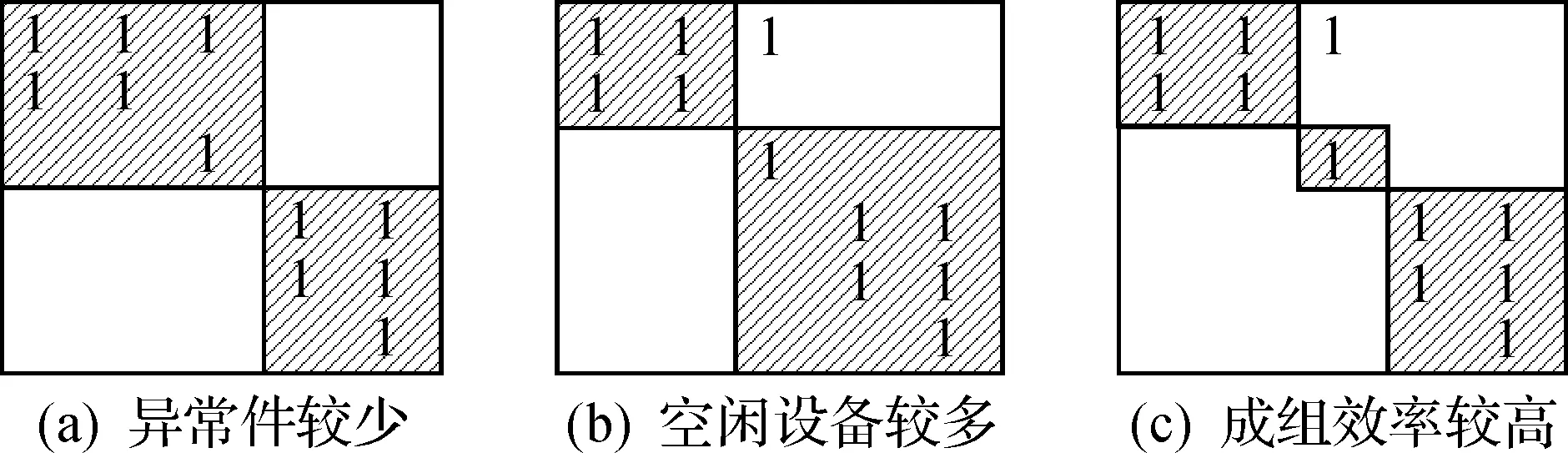
图1　三种不同的单元划分方式Fig.1　Three different ways of cell division

24种扩张路径与评价指标

2.14种扩张路径

通过对图1中不同的单元划分方式的分析，结合矩阵自身的特点，可以将矩阵中的每一个坐标点看作是一个决策点，每个决策点可以有4种选择路径，分别是不扩张、向右扩张、向下扩张和向斜下扩张.不同制造单元的划分主要由这4种不同的扩张路径形成.针对这4种路径，可以采用0～3之间的整数进行表示，如图2所示.

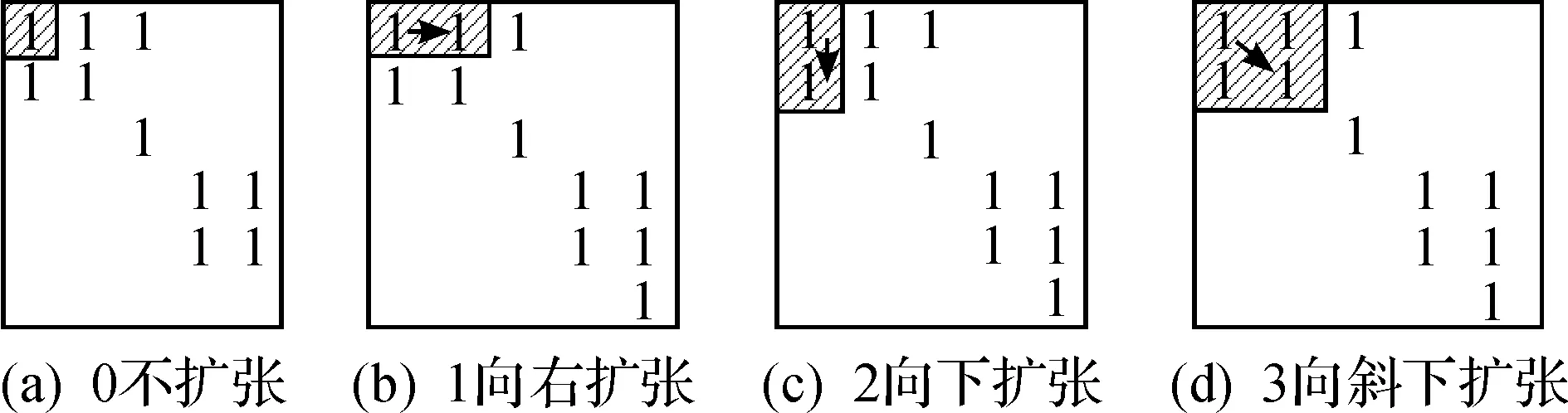
图2　4种不同的扩张路径 Fig.2　Four different expansion path

根据图2中4种不同的扩张路径，随机产生0～3之间的随机数.根据该随机数将不同的设备和零件进行分组，形成制造单元.一个制造单元中含有元素“1”的个数越多，该单元的成组效率越高，说明在该单元中可以加工更多的零件，从而能够提高设备的利用率.笔者采用单元密度来评价在形成制造单元前后，单元中元素“1”在整个单元中所占比例的变化率.单元密度可表示为

(1)

式中：N1为制造单元中元素“1”的数量；c为当前的制造单元；N0为制造单元中元素“0”的数量.

2.2评价指标

目前，评价指标主要是使用设备—零件关联矩阵中的异常零件(该零件未分配到单元中，需要跨单元加工)和每个制造单元中元素“0”所占的比率对单元成组的效率进行评价.采用Kumar和Chandrasekharan提出的单元分组效率指标作为目标函数.该评价指标对制造单元中元素“0”的数量的变化非常敏感.目标函数表示为

(2)

式中：e为设备—零件关联矩阵中元素“1”的总数量；e1为制造单元外的元素“1”(异常零件)的数量；e0为制造单元中元素“0”的数量；ψ为异常零件与矩阵中元素“1”的总数量的比率；φ为制造单元中元素“0”的数量与矩阵中元素“1”的总数量的比率.

3基于DCA的单点变异算法步骤

随着问题规模的扩大，很难根据已有的知识给出准确的单元分组数.因此，笔者提出来一种新颖的启发式算法，它能够有效的进行单元划分，从而使异常零件的数量最少.其具体的算法步骤如下：

步骤1根据DCA算法的求解结果，以矩阵的左上角第一个点为起始点，并且将该点作为决策点，记录该点的坐标.

步骤2根据4种不同的选择策略，在每一个决策点随机产生0～3之间的随机数，然后进行判断.

1) 如果随机数为0，则形成一个单元，记录该单元的坐标，同时将决策点的横纵坐标各移动1个单位，若移动后的坐标没有越界，则将其作为新的决策点.否则执行步骤3.

2) 如果随机数是1，将决策点的纵坐标向右移动一位，如果新坐标越界，则执行步骤3，否则判断新坐标位置的值是否是元素“1”，如果是元素“1”，则将该坐标点对应的设备和零件划入单元中，以该新坐标为新决策点；如果是元素“0”，判断该列是否存在其他非零元素，并且执行5).

3) 如果随机数是2，将决策点的横坐标向下移动一位，如果新坐标越界，则执行步骤3，否则判断新坐标位置的值是否是元素“1”，如果是元素“1”，则将该坐标点对应的设备和零件划入单元中，以该新坐标为新决策点；如果是元素“0”，判断该行是否存在其他非零元素，并且执行5).

4) 如果随机数是3，将决策点的行列坐标各移动一位，如果新坐标越界，则执行步骤3，否则判断新坐标位置的值是否是元素“1”，如果是元素“1”，则将该坐标点对应的设备和零件划入单元中，以该新坐标为新决策点；如果是元素“0”，判断该行或该列是否存在其他非零元素，执行5).

5) 若存在非零元素，则计算将该非零元素处对应的设备和零件划入单元前后的单元密度，同时产生一个0～1之间的随机数，如果划入前的单元密度大于划入后的单元密度，并且随机数大于0.5，则将该非零元素处对应的设备和零件划入单元，将决策序列随机数变为0，形成新的制造单元.否则，不将该非零元素划入单元中，决策点依旧是移动前的坐标值，然后执行步骤4.

步骤3将矩阵中剩余的行和列划入该单元中，将决策序列随机数变为0，从而形成一个新的制造单元.

步骤4对以上步骤不断迭代，产生一组决策序列.该序列中的每个值代表决策点所产生的0～3之间的随机值.

步骤5对产生的决策序列进行变异操作.在决策序列值的个数范围内产生随机数，该随机数决定决策序列中发生变异的决策点，该点的变异操作会导致后续的随机值发生变化.

步骤6比较变异前后目标函数值的大小，保留目标函数值较大的序列.在最终保留的决策序列中，选择目标函数值最大的决策序列作为最终的单元划分的依据.

4数值算例

为检验本算法的有效性，利用Matlab软件随机产生6种零件和10种设备组成大小为6×10的零件—设备关联矩阵，如表3所示.通过采用笔者提出的算法对关联矩阵进行求解，进而获得单元构建中最佳的制造单元数量.

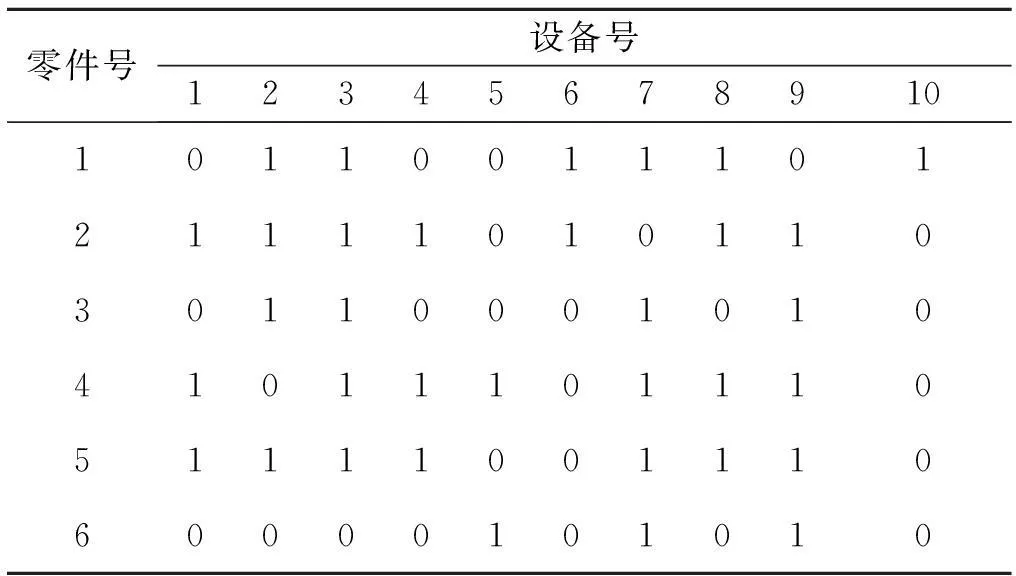
表3　零件—设备关联矩阵

利用直接聚类算法(DCA)对零件—设备关联矩阵进行变换，最终的变换结果如表4所示.

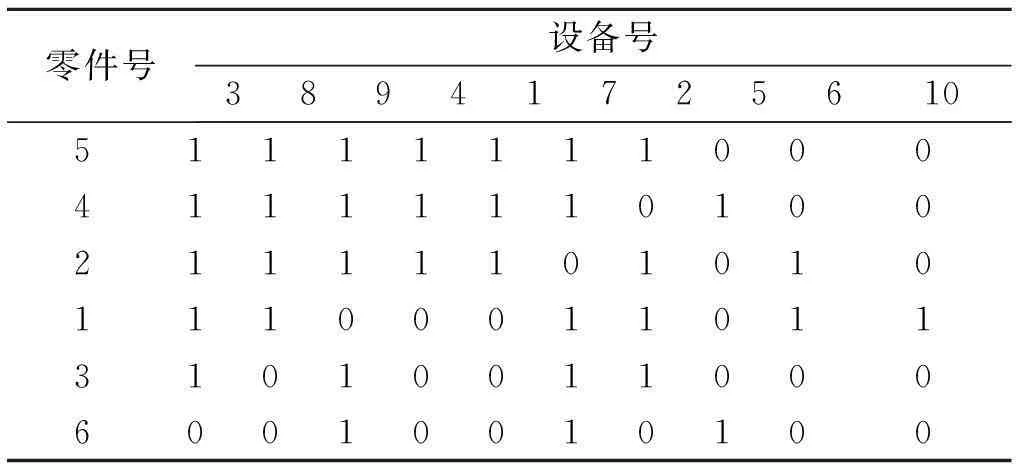
表4　行和列调整后的矩阵

由表4可知：根据DCA算法将相似零件与对应加工机器设备聚集在一起，最终形成由元素“1”组成的集中块.针对该集中块，采用笔者所提出的算法，产生10组不同的决策序列，如表5所示，而每一种决策序列都代表一种单元划分方案.

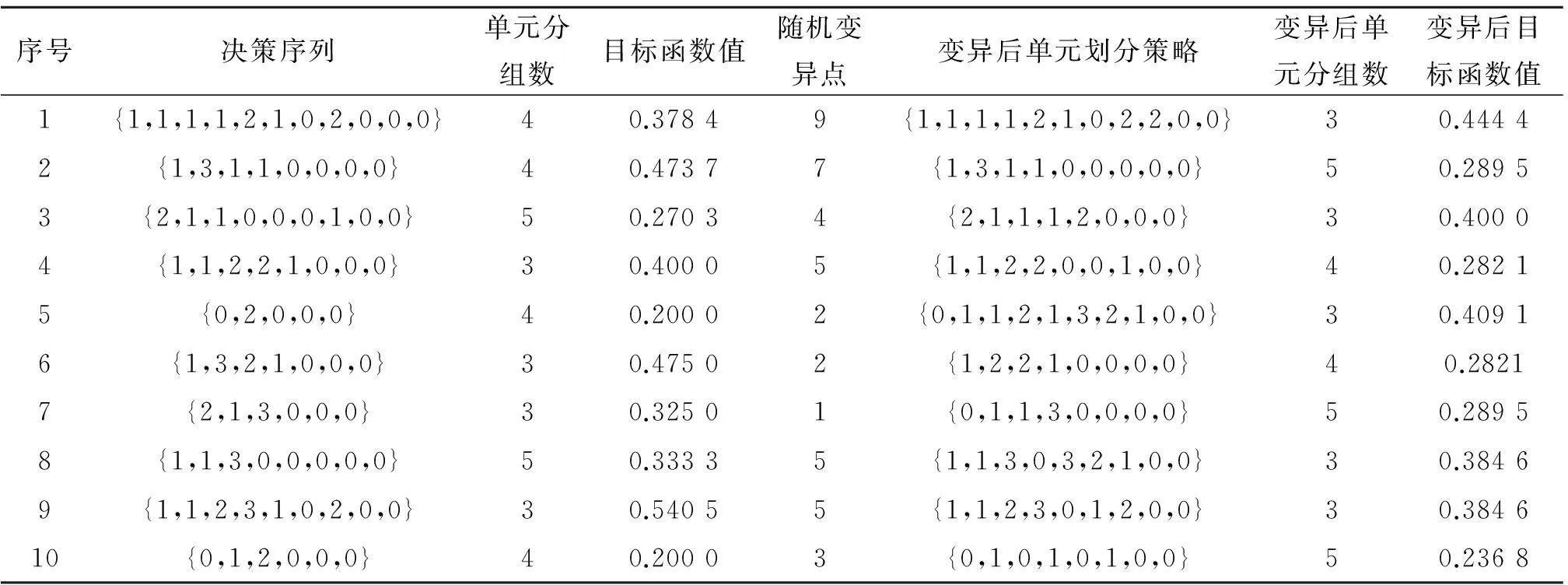
表5　单元划分的决策序列

通过对表5的决策序列进行分析，可以发现：在每一次随机产生的决策序列中，所组成的序列规模都是不一致，这也带来了单元分组数之间的差异性，从而对每一种决策序列进行评价的目标函数值优劣不一.这说明了不同的单元划分策略关系到单元构建实施成功与否的关键.在第7组的决策序列中，通过对决策序列进行多点变异，最终得到比较满意的目标函数值，而单元数量由原来的4个减少为2个.这不仅能提升单元内设备的利用率，而且可以减少企业布置生产单元的成本.

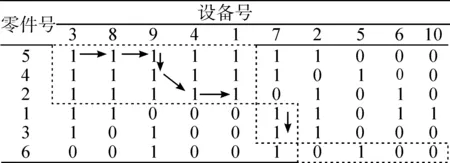
因此，针对表3随机产生的零件—设备关联矩阵，利用所提出的新颖算法，可以确定的决策序列是{1,1,2,3,1,0,2,0,0},产生3个生产单元，分别是单元1由零件{5,4,2}和设备{3,8,9,4,1}共同组成；单元2由零件{1,3}和设备{7}所组成；单元3由零件{6}和设备{2,5,6,10}共同组成.最终的目标函数值是0.540 5.该决策序列的最终决策路径，如表6所示.

表6单元划分的决策路径

Table 6Decision path of unit partition

5结论

利用直接聚类算法对零件—设备关联矩阵进行排序，将该排序结果作为新算法的初始矩阵.根据矩阵本身的特点，利用4种不同的扩张策略得到10组不同的决策序列，对每一种决策序列采取单点变异，并利用成组效率评价指标对每一种决策序列进行评价，找出其中评价指标最大的决策序列作为最终单元划分的策略.通过数值算例可以看出：对于复杂的初始关联矩阵,所提算法可以提高单元划分的成组效率，得到较满意的结果.

参考文献：

[1]王晓晴，唐家福，宫俊.基于分散搜索的多目标动态单元构建方法[J].管理科学学报，2009,12(5):44-52.

[2]WANG Xiaoqing, TANG Jiafu. Optimization of the multi-objective dynamic cell formation problem using a scatter search approach[J]. International journal of advanced manufacturing technology,2009,44(3):318-329.

[3]金晶,冯定忠，金寿松.基于负荷均衡和物流量控制的制造单元构建技术[J].轻工机械,2010,28(1):107-111.

[4]JAMAL A, LEILA H. Minimization of exceptional elements and voids in the cell formation problem using a multi-objective genetic algorithm[J]. Expert systems with applications,2011,38(8):9597-9602.

[5]余世根，鲁建厦.基于GA的固定约束条件下多目标车间设备布局问题研究[J].浙江工业大学学报，2010,38(4):401-405.

[6]马玉敏，陈炳森，张为民.基于多条工艺路线单元构建的遗传算法[J].现代设计技术，2001,18(1):18-21.

[7]范佳静,冯定忠.基于改进遗传算法的制造单元设计研究[J].中国机械工程，2011，22(1):39-43.

[8]RAFIEI H,GHODSI R. A bi-objective mathematical model toward dynamic cell formation considering labor utilization[J].Applied mathematic modeling,2013,37(4):2308-2316.

[9]NIAKAN F, ARMAND B. A Multi-objective mathematical model considering ecomomic and social criteria in dynamic cell formation[J]. Advances in information and communication technology,2014,439:46-53.

[10]ZAHIR A, HAMDI A. A mathematical approach for the formation of manufacturing cells[J]. Computers & industrial engineering,2005,48(1):3-21.

[11]陈形丰，鲁建厦，李英德,等.离散型制造企业车间布局缓冲区面积设置仿真决策研究[J].浙江工业大学学报，2010,38(3):246-256.

[12]王建维.制造单元构建的关键技术研究[D].大连：大连理工大学，2009.

[13]张传忠，李祖庚.形成单元制造的组的直接聚类算法[J].成组技术,1985，4(3):35-44.

[14]CHAN H M, MILNER D A. Direct clustering algorithm for group formation in cellular manufacturing[J]. Journal of manufacturing systems,1982,1(1):65-74.

(责任编辑：陈石平)

Research on the cell partition problem based on single point mutation algorithm

HAN Yi1,2, WANG Dezhi1, LIN Huazhen1, GU Bing1

(1.College of Economics and Management, Zhejiang University of Technology, Hangzhou 310023, China 2.Research Center for Technology Innovation and Enterprise Internationalization, Hangzhou 310023, China)

Abstract:Aiming at cell partition problem in the cellular manufacturing system, a novel algorithm, combining with the characteristics of the parts and equipment association matrix for partitioning cells is presented. During the process of cell formation，the result from the direct clustering algorithm(DCA) is adopted as an initial solution. A decision sequence is then reached according to four different expansion directions. Then, the single point mutation on the decision sequence is carried out，and the efficiency evaluation index of cell formation is used as the objective function to evaluate the algorithm. The results show that the proposed algorithm can improve the efficiency of cell partition and get better satisfactory results for those problems with complicated initial correlation matrix.

Keywords:cellular manufacturing system; direct clustering algorithm; cell number; cell formation

收稿日期：2015-10-08

基金项目：国家自然科学基金资助项目(71301147,71301148,71302051)；教育部人文社科基金资助项目(12YZCZH065)

作者简介：韩 毅(1979—)，男，辽宁沈阳人，副教授，博士，研究方向为生产批量计划与调度、智能优化算法与应用、供应链优化以及逆向物流等，E-mail:hanyi@zjut.edu.cn.

中图分类号：TH163

文献标志码：A

文章编号：1006-4303(2016)02-0202-05