气相F因子对规整填料内液膜流动的影响

李相鹏，杨立军，李　锋

(浙江工业大学 机械工程学院，浙江 杭州310014)



气相F因子对规整填料内液膜流动的影响

李相鹏，杨立军，李锋

(浙江工业大学 机械工程学院，浙江 杭州310014)

摘要：采用CFD数值模拟方法研究规整填料内液相参数改变时气相F因子对气液两相流体动力学的影响，建立基于流体力学软件FLUENT并与Navier-Stokes方程和VOF方法相结合的二维模型，湍流结构模拟采用RNG K-ε模型.对Mellapak 250Y型金属板波纹填料在不同液相流量和表面张力下气相F因子对液膜流体动力学的影响进行模拟分析，并与文献实验结果对比验证.结果表明：不同液相参数下，受气相F因子的影响，液膜逐渐由稳定流动变为液滴；持液量随流量的增大而增加，随表面张力的增加先增大后减小；当流量超过临界值时，有效传质面积突然增大，而有效传质面积随表面张力的增加而持续增大；受气相F因子和液相参数的影响，速度分布Vy存在临界值，当液相参数大于临界值时Vy波动较大，液面变化较大.

关键词：气相F因子；气液两相流；规整填料；液相流量

规整填料塔具有效率高、通量大、压降低和放大效应小等优点，已在诸多工业分离过程中得到广泛应用[1].目前，对于规整填料塔的研究主要集中在传质过程和流体力学的实验方面[2]，但对于复杂的流场、温度场和浓度场等的实验研究，并未形成一个普遍适用的经验模型，而仅仅适用于特定的实验范围，因此所得出的预测结果具有一定的局限性[3].随着计算机技术的广泛应用，计算流体力学(CFD)已经成为研究流体动力学的重要分析方法[4].Van Gulijk[5]利用CFD软件对填料内液相流动及径向返混行为进行了研究，提出了“Toblerone”三维简化模型.在此基础上Van Baten等[6-8]建立针对KATAPAK-S型反应精馏规整填料的8孔道模型，模拟液相轴向和径向的返混情况，得出的返混系数与实验值近似.Szulczewaka B等[9]建立了Mellapak 250Y型金属填料的二维两相逆流模型，对多种形式波纹板的气液两相逆流流动的过程进行了模拟，并将气速、液速和液体的物理性质对气液相界面面积的影响进行模拟研究.Raynal等[10]为研究规整填料液膜厚度、持液量等，建立了“Z”状流动路线的二维两相流模型，并进一步针对界面传质进行了研究.浙江工业大学李相鹏[11]通过模拟研究液相物性对规整填料内气液两相流的影响，重点研究了密度、粘度改变时对液膜流动的影响；李相鹏等[12]模拟研究不同气相F因子对液膜流体动力学的影响，特别是各工况下液膜动态运动分布、持液量以及有效传质面积的变化情况.

笔者结合前人的研究结果，建立填料的二维模型，并结合Navier-Stokes方程和VOF模型，研究气液两相流在填料内的流动情况，并通过改变液相参数，研究气相F因子对液膜分布状况、两相流场的结构变化、速度分布以及有效传质面积的影响情况.

1计算模型

1.1建模

Mellapak 250Y型金属板波纹填料参数如表1所示.根据结构尺寸，选其中的5个波纹建立二维气液两相流模型，其中模型总长180 mm，气相入口9 mm，气相出口63 mm，液相入口5 mm，液相出口3 mm，波纹板间距为24 mm如图1(a)所示.气相由气相进口进入，在压力的作用下穿过曲折的流道，并最终由气相出口流出，在此过程中，气相与由液相进口进入的液相在曲折的流道中不断地接触，达到传质、混合的目的，液相最终由液相出口流出；图1(b)为局部的网格、尺寸图，网格为结构化网格，利于跟踪复杂的界面变化，同时在界面区域对网格进行加密.

表1　Mellapak 250Y型填料参数

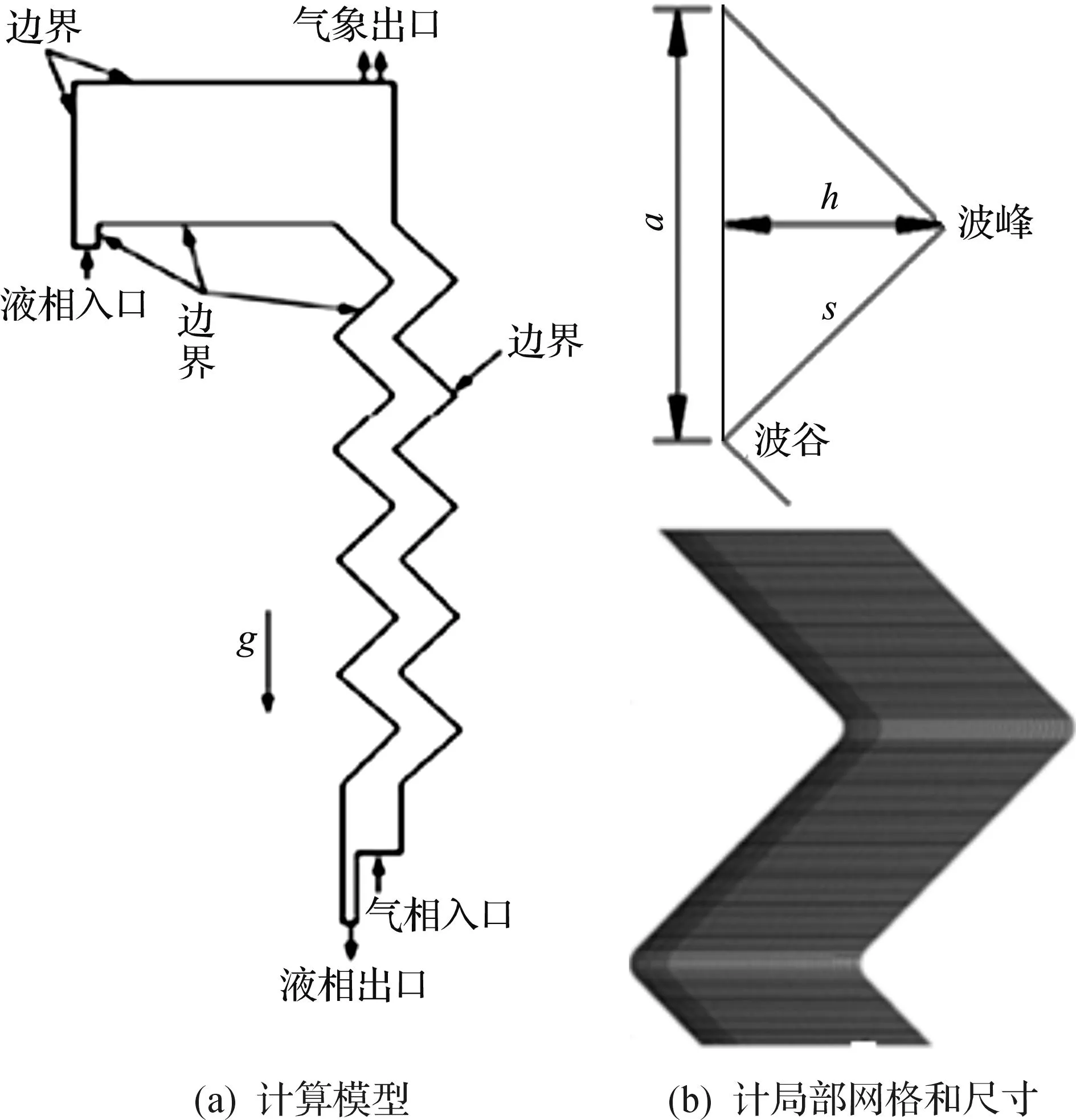
图1　模型结构示意图Fig.1　Model structure diagram

1.2边界条件和计算方法

设置边界条件，气相入口和液相入口为velocity-in，气相出口和液相出口为pressure-out，壁面无滑移，计算方法为VOF多相流模型和RNGK-ε气液两相湍流结构相结合，这种方法能够更为准确的跟踪气液两相界面的变化情况，以及液膜的形成和发展过程.

2模型的验证

为了验证CFD模型和计算方法的准确性，以文献[14]中的复杂表面液膜流动实验数据为基础，采用相同的试验工况建立模型，并将实验结果与模拟结果相互对比.根据文献[14]中规整填料的结构形式，选用其中的C型表面结构作为实验对象，其表面结构的圆弧半径为1.587 5 mm，圆弧之间间距为0.2 mm，单节波纹总长3.375 mm；以硅油为对比模拟介质，其物理参数如下：密度969 kg/m3，粘度0.088 5 Pa·s，表面张力0.021 4 N/m，单位宽度液相流量为1.979×10-6m3/(s·m).如图2所示，将流动稳定时的液膜状态与CFD模拟结果对比发现：两者契合度较好，误差较小，绝对值偏差均小于10%，平均绝对偏差为3.06%，所建立的模型符合要求.

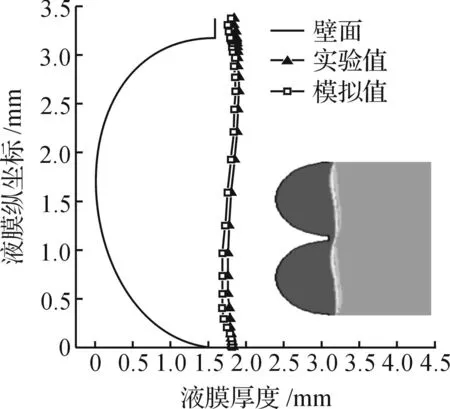
图2　模拟结果与实验结果的对比Fig.2　Comparison of simulation result and experimental result

3液相流量改变时气相F因子对液膜流动的影响

液膜流动状态主要是由气相因子决定的，气相作用在液膜表面使得液膜发生变化，但气相F因子的作用会受到液相流量的影响，因此在此以空气-甲醇为模拟对象，研究单位宽度液相流量改变时逆向气载对气液两相流体动力学特性的影响，单位宽度液相流量Q分别为1.5×10-4，3.0×10-4，4.5×10-4，6.0×10-4m3/(s·m)，气相进口速度取2 m/s(气相F因子1.66 Pa0.5).

3.1对液膜流速度场分布的影响

由图3可得规整填料内的气液流动状况，液膜速度沿波纹板表面呈周期性变化，靠近液膜的气体在曳力的作用下一同下降，并与其他气体产生剪切作用，从而在液膜附近形成回流.

图3　气液两相流分布云图Fig.3　Contours of gas-liquid

图4为不同单位宽度液相流量时，气相F因子作用下液膜自由界面沿填料表面分布图.从图4可得：单位宽度液相流量Q从1.5×10-4～4.5×10-4m3/(s·m)时，在气相F因子作用下液膜表面分布基本一致，液膜贴合在填料表面，厚度在6.0×10-4m左右，只有微小波动，且随着时间的变化不大，只有在波纹板波峰和波谷处液流发生积聚，尤其在波纹板波谷处液流积聚比较明显，4.5×10-4m3/(s·m)即为单位液相流量的峰值，当小于峰值时，液膜流动稳定，而当液体流量超过峰值时，液膜则会发生剧烈波动，以Q=6.0×10-4m3/(s·m)为例，气相F因子的作用变大，液膜波动剧烈，破坏了液膜平衡，液膜厚度达到9.9×10-4m，且随时间变化很大，部分液流被气流吹起形成小液滴.

单位液相流量改变时，气相F因子对速度分量vx和vy的影响基本一致，现只分析vy变化情况，如图5所示，速度分量vy沿波纹板表面呈周期性变化，波峰处的速度vy>0，说明在波纹板波峰处液膜有向上的流动；单位宽度液相流量从1.5×10-4m3/(s·m)增大到4.5×10-4m3/(s·m)时，随着单位宽度液相流量的增大，气相F因子作用下vy峰值有所变小，而vy谷值几乎不变；当Q=6.0×10-4m3/(s·m)时，即液相流量超过峰值时，气相F因子作用下，液膜波动剧烈，vy峰值急剧变小.

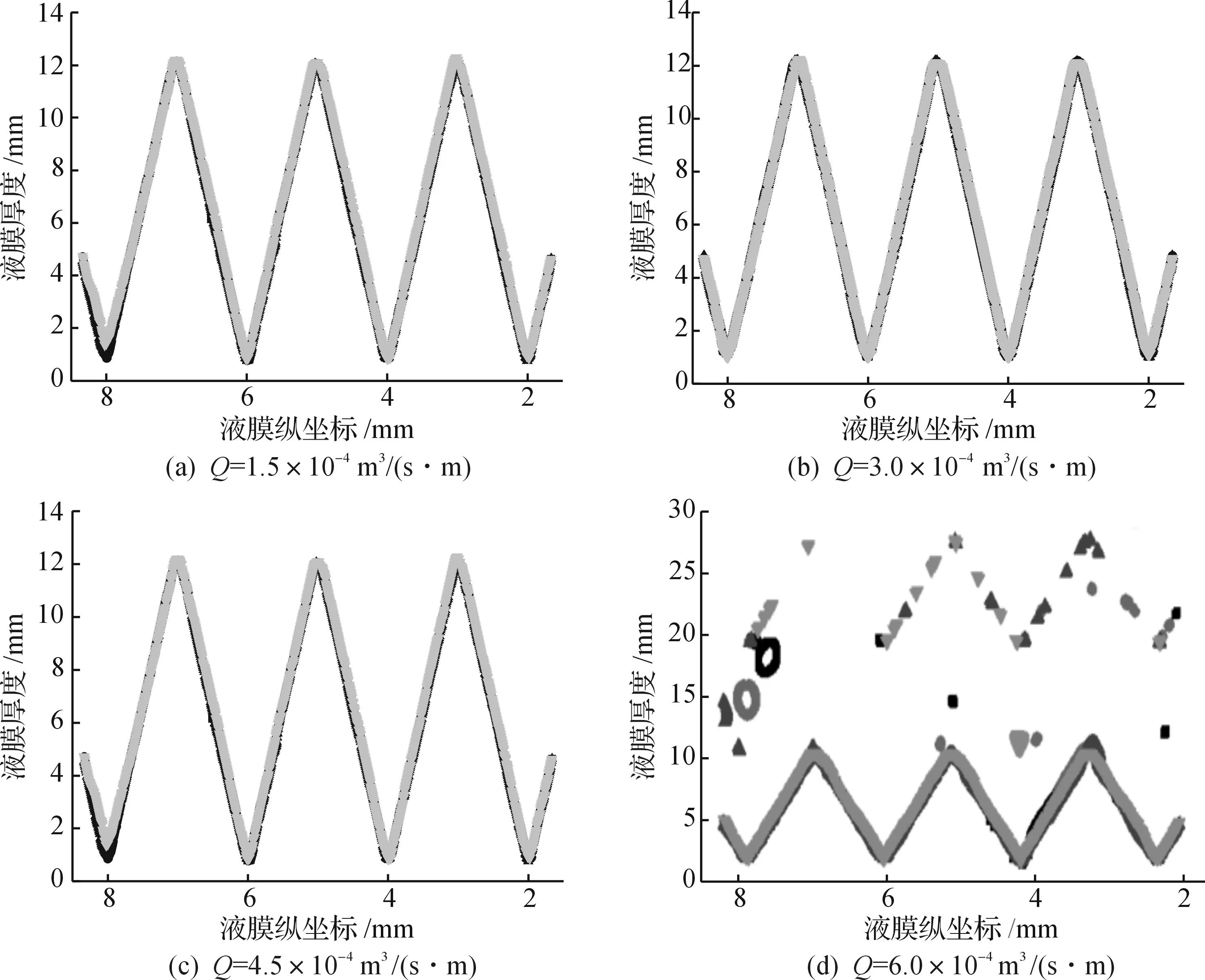
图4　液膜分布随液相流量Q的变化曲线Fig.4　Distribution of liquid surface with different Q

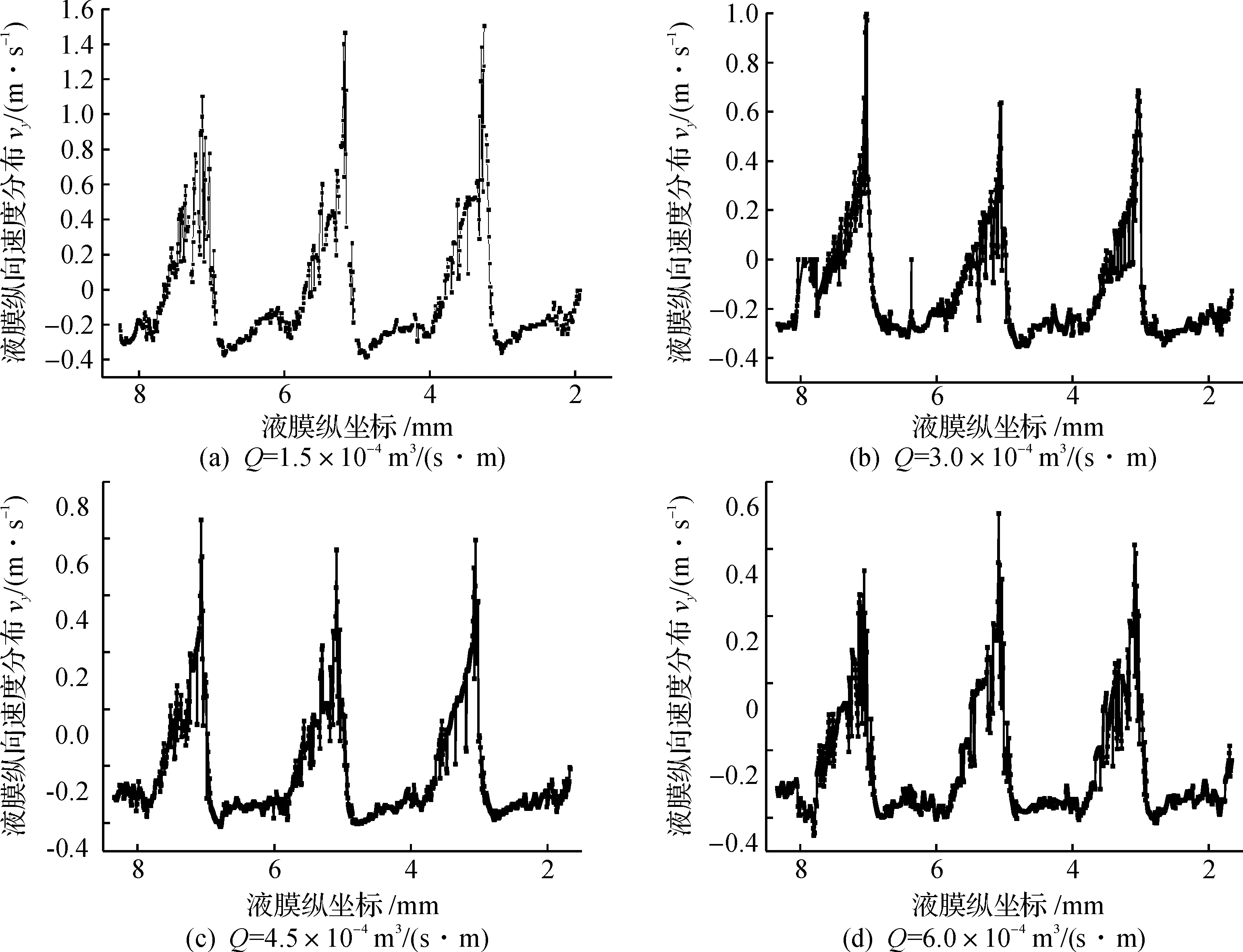
图5　速度分布Vy随液相流量Q的变化曲线Fig.5　Distribution of Vy with different Q

3.2对液膜传质参数的影响

图6为单位宽度液相流量改变时，气相F因子对持液量hL及有效界面传质面积与填料比表面积比值ae/ap的影响.单位宽度液相流量Q从1.5×10-4m3/(s·m)增大到4.5×10-4m3/(s·m)时，随着液相流量的增加，在气相F因子作用下，持液量hL随之增大，但增幅较小；当液相流量Q增大到6.0×10-4m3/(s·m)，流量超过临界值时，hL增幅较大，而ae/ap的变化情况基本类似；在单位宽度液相流量Q从1.5×10-4m3/(s·m)增大到4.5×10-4m3/(s·m)时几乎不变，当单位宽度液相流量Q增大到6.0×10-4m3/(s·m)时，流量超过峰值，气相F因子作用下，液膜波动剧烈，有效传质面积增幅较大.

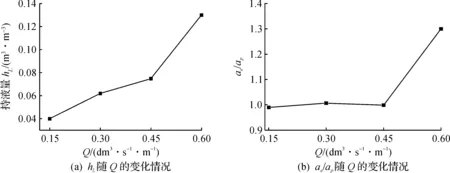
图6　不同Q下，hL和ae/ap的变化曲线图Fig.6　Curve of hL and ae/ap with different Q

4表面张力改变时气相F因子对液膜流动的影响

气相F因子对液膜流动状态的影响同样会受到液相流量的作用，在气液两相体系中，表面张力的作用主要是通过减小界面的面积而使自由能最小化，所以在液相物性中表面张力的作用至关重要.模拟时，表面张力σ选取0.02，0.04，0.06，0.08 N/m，将单位宽度液相流量Q设为3.0×10-4m3/(s·m).

4.1对液膜流速度场分布的影响

由图7可得：表面张力σ从0.02 N/m增大至0.04 N/m时，在气相F因子作用下液膜厚度有一定增大，但增幅不大，液膜平均厚度为6.0×10-4m左右，此时液膜达到临界值；当表面张力σ超过0.04 N/m后，临界状态打破，在气相F因子的作用下液膜发生波动，气流吹动液流形成小液滴，并且液膜厚度逐渐减小；表面张力σ在0.06 N/m时液膜平均厚度为6.59×10-4m，表面张力σ在0.08 N/m时液膜平均厚度为5.58×10-4m.

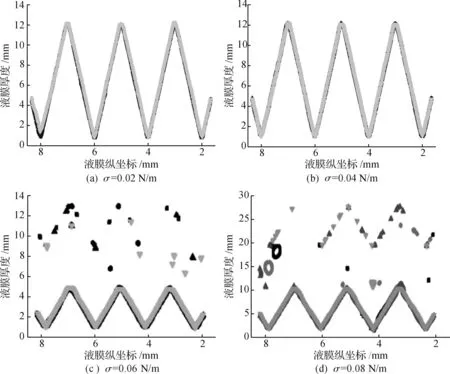
图7　液膜分布随表面张力σ的变化情况Fig.7　Distribution of liquid surface with different σ

表面张力对液膜界面速度分量vx和vy的影响基本一致，图8为界面速度分量vy分布曲线图，表面张力σ从0.02 N/m增大至0.04 N/m时，速度分量vy沿波纹板表面呈周期性分布，在气相F因子作用下vy峰值随着表面张力增大有所减小；当表面张力σ为0.06，0.08 N/m时，液膜发生波动，但vy主体变化情况几乎不变，且随着表面张力增大vy峰值继续减小.

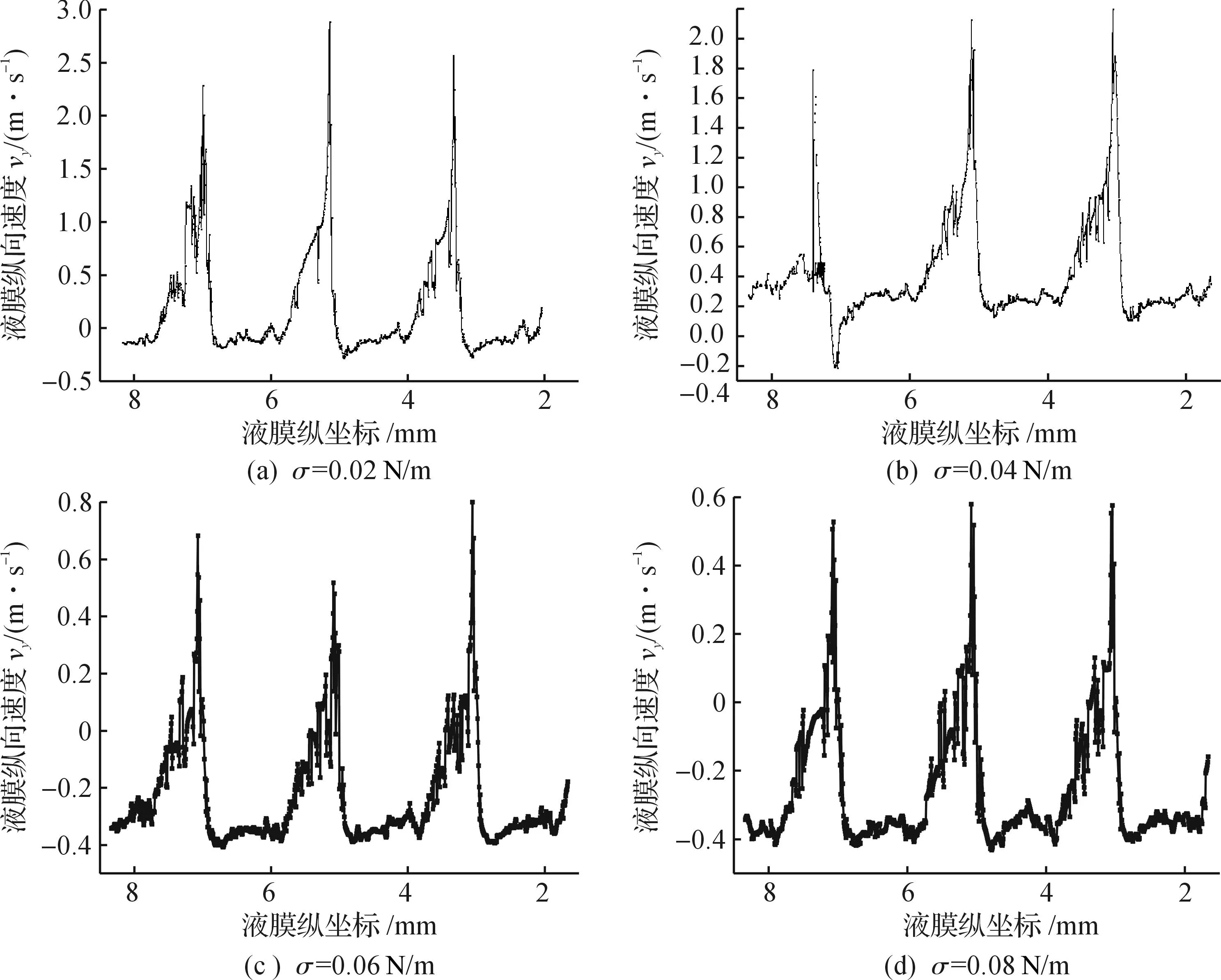
图8　液膜速度分布Vy随表面张力σ的变化情况Fig.8　Distribution of Vy with different σ

4.2对液膜传质参数的影响

图9为表面张力σ改变时逆向气载对持液量hL及有效界面传质面积与填料比表面积比值ae/ap的影响.从图9发现：表面张力σ从0.02 N/m增大至0.04 N/m时，在气相F因子作用下持液量hL随表面张力的增大而增加；表面张力σ超过0.04 N/m后，即表面张力超过临界值时，持液量hL随表面张力的增大而减少；而传质面积与填料比表面积比值ae/ap随表面张力的增大而增加，但是增长趋势不明显.

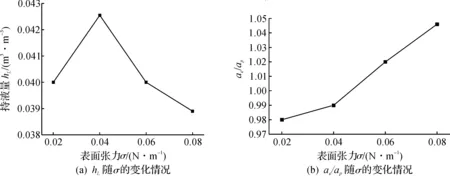
图9　hL和ae/ap的变化曲线图Fig.9　Curve of hL and ae/ap

5结论

通过对Mellapak 250Y型金属板波纹填料建立二维模型，分析当改变单位宽度液相流量Q和表面张力σ时，填料表面的液膜厚度、流动情况以及气相F因子对持液量hL和传质面积与填料比表面积比值ae/ap的影响情况.模拟结果表明：随着单位宽度液相流量Q和表面张力σ的变化，填料表面均有一层稳定的液膜，但在气相F因子作用下，液膜流动会发生变化，并在波峰、波谷处发生聚集；随单位宽度液相流量Q的增加，流道变窄，气相F因子作用增大，液膜波动剧烈，液膜厚度随之增大；速度分量vy波动幅度增大，并有液滴形成；hL和ae/ap也随之增大；而随着表面张力σ的增加，稳定液膜流产生波动，形成液滴；速度分量vy主体不变，峰值减小；气相F因子与表面张力σ共同作用下会使ae/ap值随之增大，但hL值却先增大后减小.同时，模型采用FLUENT软件，可以更为直观的得出液膜在不同液相参数时随时间的变化情况，这为得出临界条件、设置合理的操作参数提供了便利，同时FLUENT还可以随意改变各项参数，为得出不同状态下的试验参数提供了方便，而且节约了大量的时间和资金，也为装置结构的改进提供参考.

参考文献：

[1]裘俊红，陈国标，计建炳.波纹板规整填料塔液体分布[J].化工学报，2003，54(5):646-652.

[2]胡晖，徐世民，李盡钢.大型填料塔技术及其工业应用[J].现代化工，2005，25(7):53-55.

[3]陈江波，刘春江.计算流体力学方法模拟规整填料塔内流体流动行为的研究进展[J].石油化工，2007，36(9):961-965.

[4]张兆鑫，赵元虎，徐奔驰.基于CFD法的小型风机非扭曲叶片气动性能分析[J].浙江工业大学学报，2013，41(1):68-72.

[5]VAN C G. Using computational fluid dynamics to calculate transversal dispersion in a structured packed bed Computers[J]. Computers & chemical engineering,1998,22:767-770.

[6]VAN BATEN J M, KRISHNA R. Liquid-phase mass transfer within KATAPAK-S structures studied using computational fluid dynamics simulations[J]. Catalysis today,2001,69:371-377.

[7]VAN BATEN J M, ELLENBERGER J, KRISHNA R. Radial and axial dispersion of the liquid phase within a KATAPAK-S structure: experiments vs CFD simulations[J]. Chemical engineering science,2001,56:813-821.

[8]VAN BATEN J M, KRISHNA R. Gas and liquid phase mass transfer within KATAPAK-S structures studied using CFD simulations[J]. Chemical engineering science,2002,57:1531-1536.

[9]SZULCZEWAKA B, ZBICINSKI I, GORAK A. Liquid flow on structured packing: CFD simulation and experimental study[J]. Chemical engineering technology,2003,26(5):580-584.

[10]RAYNAL L, BOYER C, BALLAGUET J P. Liquid holdup and pressure drop determination in structured packing with CFD simulations[J]. The canadian journal of chemical engineering,2004,82:871-879.

[11]李相鹏，汪蓉梅.液相物性对规整填料内气液两相流的影响[J].化学工程，2014，42(1):40-44

[12]李相鹏，李锋，张超.规整填料内气相载荷对液膜流动特征的影响[J].中南大学学报(自然科学版)，2015，46(4):1239-1246.

[13]王树楹.现代填料塔技术指南[M].北京:中国石化出版社，1998:9.

[14]ZHAO L Q, CERRO R L. Experimental characterization of viscous film flows over complex surfaces[J]. International journal of multiphase flow,1992,18(4):495-516.

(责任编辑：陈石平)

Influences of countercurrent gasFfactor on dynamics of liquid film flow over structured packing

LI Xiangpeng, YANG Lijun, LI Feng

(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:The influences of F factor in different liquid parameters on the hydrodynamics simulation of gas-liquid two-phase flow in the structured packing were simulated using the CFD numerical techniques. A 2D model based on Navier-Stokes equations and VOF method was developed based on the platform of FLUENT, and the turbulent structure was modeled with RNG K-ε model. The simulations were conducted to study the variations of liquid film hydrodynamic with F factor at different liquid flow rate, surface tension over Mellapak 250Y corrugated packing sheet, and the model was validated by the experimental results presented in literature. The results show that at the different liquid parameters, because of the impact of F factor, the liquid film from a steady flow into droplets; the liquid holdup increases with the Q, decreases with the increase of the σ; When the flow exceeds a critical value, a sudden increase in the ae/ap, and the ae/ap increase with the increase of the σ; as the influence of F factor and liquid parameters, the Vy has a critical value, when the phase parameter is greater than the critical value, the Vy changes in the larger level.

Keywords:F factor; gas-liquid two-phase flow; structured packing; liquid flow rate

收稿日期：2015-09-14

基金项目：浙江省自然科学基金资助项目(Y20110169)；“十二五”科技支撑计划项目(2011BAK06B02)

作者简介：李相鹏(1977—)，男，湖南宁乡人，副教授，主要从事热能工程、化工过程等数值模拟与优化研究，E-mail：rocleexp@zjut.edu.cn.

中图分类号：TQ028.4

文献标志码：A

文章编号：1006-4303(2016)02-0195-07