深空通信中码率兼容原模图LDPC码的设计
2016-06-16刘勇秦亮汪振兴
[刘勇 秦亮 汪振兴]
深空通信中码率兼容原模图LDPC码的设计
[刘勇 秦亮 汪振兴]
摘要针对深空通信信道的时变特性,文章基于ARAPA原模图提出了一种适用于深空通信的码率兼容LDPC码的构造方法。这种码率兼容的LDPC码字采用矩阵扩展的方法构造,具有较低的译码门限,从而更有利于降低误码平层。此外,对ARAPA原模图分两次进行拓展,使得所构造的码率兼容LDPC码的校验矩阵具有准循环特性,从而能够进行高速的译码。仿真结果表明:与基于AR4JA原模图构造的码率兼容LDPC码相比,文章构造的码率兼容LDPC码的性能尽管与之相近,但是其具有更低的译码门限和译码计算复杂度,尤其是在高码率时具有更优越的性能,在BER为 时可获得大约0.2dB的性能增益。
关键词:深空通信LDPC码原模图码率兼容译码门限
刘勇
广东省电信规划设计院有限公司。1997年毕业于重庆邮电大学计算机通信专业,2007年获得华南理工大学电子与通信工程硕士专业学位。一直在通信行业工作了近20年,主要从事过GSM移动通信技术研究、TD-SCDMA技术和设备研发,参与了中国联通WCDMA、中国移动LTE等移动通信网络的建设设计,在通信行业经验丰富。
秦亮
广东省电信规划设计院有限公司。
汪振兴
广东省电信规划设计院有限公司。
引言
由于深空通信具有传输距离遥远、时延大、信号能量衰减严重等特点,因而高性能、低复杂度的信道编码技术成为保证深空通信系统可靠性和有效性的一项关键技术[1]。对于实际的深空通信系统而言,往往需要根据信道的环境变化实时地改变发送码字的码率以确保信号的可靠传输,因此对深空通信中码率兼容码字的设计展开研究具有现实意义。
低密度奇偶校验(Low-DensityParity- Check,LDPC)码[2]具有并行的译码结构,更适于高速硬件实现,错误平层更低,被认为是迄今为止纠错性能最好的码[3]。2003年,美国宇航局(NASA)的空气动力实验室(JPL)首次提出了原模图(Protograph)LDPC码[4],弥补了传统LDPC码编码复杂度较高的不足,其设计的AR4JA码[5]于2006年由太空数据系统咨询委员会(Consultative Committee for Space Date Systems,CCSDS)推荐给NASA作为深空通信的标准码型。
目前,实现原模图码率兼容的主要方法有打孔(puncture)和扩展(extension)两种。针对原模图的打孔,虽然操作简单但是随着打孔所得码字的码率不断增大,其译码门限值离香农限的距离会逐渐增大,因此仅仅依靠打孔并不能在较大码率范围内得到性能良好的码字[6]。为了能够在更大码率范围内,得到性能良好的码率兼容原模图LDPC码,Nguyen等人提出了一种基于AR4JA原模图的扩展构造码率兼容原模图LDPC码的方法[7]。然而鉴于深空通信的特点,其采用的码率兼容原模图LDPC码需具备更优越的性能、更低的译码门限和译码计算复杂度,针对这一问题,本文提出了一种基于ARAPA原模图[8]的矩阵扩展构造码率兼容原模图LDPC码的方法。
深空应用的LDPC码采用原模图LDPC码,选定的码率是1/2,2/3,4/5,信息位长度有1024,4096,16384[1]。根据这些要求,本文设计了一种基于ARAPA原模图的扩展构造适用于深空通信系统的码率兼容LDPC码。由于该系列码字采用性能优于AR4JA原模图的ARAPA原模图作为母码进行扩展,故其产生的子码能够很好地继承了母码的优越性能。
本文后续部分的组织如下:首先定义了原模图LDPC码,然后介绍了基于ARAPA原模图构造码率兼容原模图LDPC码的方法,接着给出了在AWGN信道下,本文提出的码率兼容原模图LDPC码的性能仿真以及和基于AR4JA原模图构造码字的性能比较,最后陈述了本文的结论。
1 原模图LDPC码
1.1原模图LDPC码的基本原理
所谓原模图,是指节点数量相对较少,图中允许有重边的Tanner图。原模图LDPC码属于多边类LDPC码的一个子类。一个原模图G=( V,C,E)包含变量节点集合V,校验节点集合C和边集合E。每条边e=( v,c)∈ E连接一个变量节点v∈ V和一个校验节点c∈ C。作为一个简单的例子,考虑如图1所示的一个原模图:

图1 原模图G
通过对原模图复制,并对图中相同类型节点间的边置换去掉重边,就可以扩展得到不同大小的图。对图1复制3次如图2:

图2 原模图G复制3次
对图2中相同类型节点间的边置换后如图3:
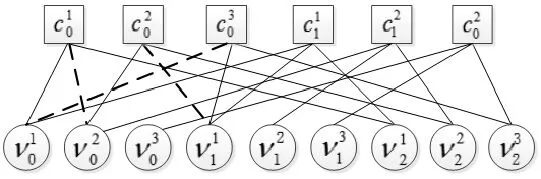
图3 相同类型节点间的边置换
图3这种Tanner图为导出图,其对应的LDPC码称之为原模图LDPC码。由此可得原模图LDPC码的构造过程:首先设计一个原模图,然后对原模图进行N次复制,最后把N个相同类型的变量节点和校验节点之间的边置换。原模图在扩展时采用的置换方式不仅会影响所得码的性能,而且还决定了硬件实现的复杂度,因此针对原模图基于复制-置换的拓展算法进行研究极具现实意义。
1.2ARAPA码
ARAPA码是一种基于ARA码改进得到的原模图LDPC码[8],它不仅具有较低的译码门限和线性码距特性,而且保持了其编码的简易性和译码的较低复杂度。图4给出了ARAPA码的原模图:

图4 ARAPA原模图
图4中实心圆表示传入信道的传输码元;空心圆表示打孔码元;包含加号的圆表示校验节点。则ARAPA原模图相应的基础矩阵B如下:

由图1可知,传输码元数为N=4+2m,打孔码元数P=1,校验节点数M=3,则该码的码率为:

研究表明,ARAPA原模图LDPC码的编码简单,译码器具有码率兼容特性,迭代译码门限低。另外,它具有线性码距特性,减少了不可检错误,从而误码平层比较低。与AR4JA码相比,ARAPA码与之性能相近甚至略优,但是由于其节点的平均度数低于AR4JA码,从而使得其译码计算法复杂度更低。
2 码率兼容原模图LDPC码的构造
码率兼容LDPC码是由一个嵌套结构组成,它能够在一定码率范围内采用单个编译译码器工作[9]。由于深空通信通常采用原模图LDPC码作为其信道编码,同时为了适用于深空通信的实际应用,真正意义上的码率兼容往往需要保证这一系列码字信息位长度的不变,故本方案采用原模图设计信息位长度不变的码率兼容LDPC码。
扩展是选取一种高码率及性能良好的码字作为母码,然后通过不断地增加额外的校验比特来获取一系列低码率的子码,而矩阵扩展是最早提出的一种扩展方法[10]。
本方案首先采用高码率、性能较好的ARAPA原模图进行矩阵扩展,即对APAPA原模图的母码基础矩阵同时增加相同的行(校验节点)数和列(变量节点)数,以获得低码率的原模图,然后对所得到的原模图进行一定次数的拓展即可得到一定码长的码率兼容原模图LDPC码。在与之对应的Tanner图中,新增的变量节点仅仅与新增的校验节点相连,从而保证了高码率的码字内嵌于低码率的码字之中。
2.1基于ARAPA原模图的矩阵扩展
一种基于4/5码率的ARAPA原模图矩阵扩展的码率兼容校验矩阵结构如图5。
4/5 码率的ARAPA原模图如图4。其原模矩阵B4/5如图5。

图5 一种基于ARAPA原模图矩阵扩展的码率兼容设计

在上述原模图基础矩阵中,度数最大的最后一列作为原模图打孔节点。例如,为了得到1/2到4/5码率范围的码率兼容原模图LDPC码,故通过对4/5码率的基础矩阵每次增加一行一列,从而获得一系列码率兼容原模图LDPC码字,其码率分别为:

n表示母码基础矩阵新增加的行数与列数的总数。
对4/5码率的原模基础矩阵经过6次一行一列的扩展,最终可得7种码率的码率兼容原模图LDPC码。最终得到的一种1/2码率的原模图基础矩阵如下:

上述原模矩阵包含了另外6个高码率的原模基础矩阵。为确保高码率的码字内嵌于低码率的码字之中,每次新增一列时仅在新增的一行处有非零元素,在确定新增的每一行里面非零元素的分布时,可以通过以译码门限值为标准展开搜索,从而得到较好性能的码率兼容的原模图。
为了方便与文献[7]构造的码率兼容原模图LDPC码比较,本文的原模矩阵的行列扩展过程与文献[7]相同,即每一次扩展过程中相应行新增的元素分布相同。如式(5)所示,其基于4/5码率扩展得到的1/2码率原模图的扩展部分与文献[7]相同。
译码门限是衡量一个原模图性能的重要因素,低的译码门限值意味着更低的误码平层和更高的编码增益。因此,表1给出了本文设计的各个码率下的码率兼容原模图LDPC码的迭代译码门限值,迭代译码门限值的计算采用PEXIT算法[11]。作为对比,表2给出了文献[7]设计的相应的多个码率下基于AR4JA原模图的码率兼容码的迭代译码门限值。

表1 码率兼容ARAPA的迭代译码门限
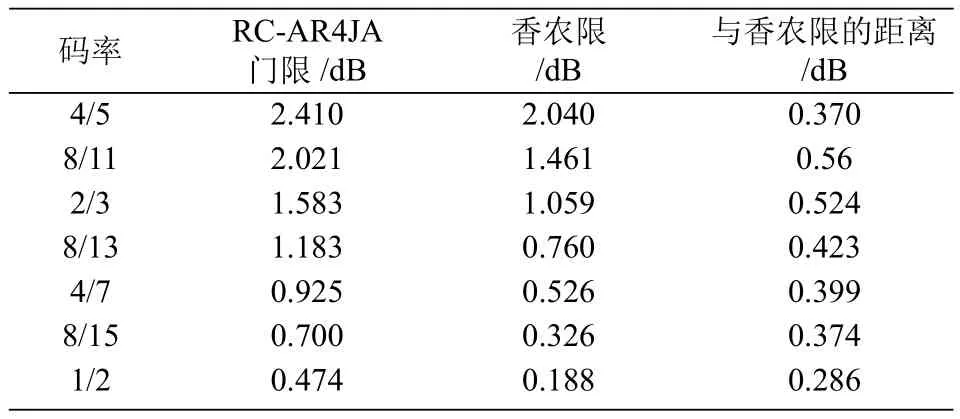
表2 码率兼容AR4JA的迭代译码门限
通过表1可以发现,本文设计的这类码率兼容原模图LDPC码的迭代译码门限距信道容量都在0.5dB以内。将表1与表2的数据对比,说明了本文设计的这类码率兼容码具有更低的译码门限值,从而更加有利于降低错误平层(error floor)。
LDPC码所对应的Tanner图中节点的平均度数往往决定了该类LDPC码的译码计算复杂度。为了与码率兼容AR4JA码对比,表3给出了本文设计的7种码率兼容ARAPA原模图和码率兼容AR4JA原模图的变量节点的平均节点度数和校验节点的平均度数。

表3 码率兼容的ARAPA与AR4JA节点平均度数
通过表3中的数据对比可知,码率兼容ARAPA原模图的变量节点与校验节点的平均度数,均小于码率兼容AR4JA原模图的变量节点与校验节点的平均度数,说明了本文设计的码率兼容ARAPA码的译码计算复杂度低于文献[6]中的码率兼容AR4JA码的译码计算复杂度。
2.2原模图的拓展算法
根据深空通信对所采用原模图LDPC码的一些相关要求,对上述原模图进行复制-置换,也即拓展(Lifting)后,就能够得到长度不同的码率兼容LDPC码。由于具有循环置换特性的原模图LDPC码能够进行高速的译码[12],故本文对所设计的码率兼容的原模图分两步进行拓展。首先,采用PEG算法[13]分别对各个码率的原模图拓展4次以移去重边,然后再次采用PEG算法进行若干次拓展以得到长度一定的具有循环置换特性的码率兼容原模图LDPC码。
3 性能仿真
考虑到本文设计的码率兼容码字需要满足深空通信的一些关于LDPC码的码率、码长的要求,本文在第2次采用PEG算法拓展时选择的拓展次数为32,得到了由维数为32的循环置换矩阵组成的一系列信息位长度k=1024的码率兼容原模图LDPC码,其拓展后码字的围长为6。
我们采用上一部分的方法基于ARAPA原模图构造码率兼容LDPC码,并对这种码率兼容的码字进行了仿真。仿真在AWGN信道下进行,采用BPSK的方式调制,采用BP算法译码,最大迭代次数设置为100。
图6给出了基于ARAPA原模图的扩展,码率范围为1/2到4/5的7种码率兼容原模图LDPC码的BER性能仿真曲线。

图6 7种信息位长度k=1024的码率兼容ARAPA原模图LDPC码的性能
由图6可知,7种基于ARAPA原模图的码率兼容LDPC码的BER性能曲线从右至左,随着码率的降低,性能越来越好,而且各个码率下的原模图LDPC码的BER曲线具有良好的“瀑布”特性,在BER低至10-6处,未出现错误平层。而且这7种码率中包含1/2,2/3,4/5

图7 3种信息位长度k=1024的码率兼容ARAPA原模图
LDPC码与码率兼容AR4JA原模图码字性能比较这3种深空通信选定的码率,k=1024的信息长度也符合深空通信关于LDPC码的码长要求。
图7给出了基于本文所提出的构造方法得到的信息位长度k=1024,码率分别为1/2,2/3,4/5这3种深空通信选定码率的码率兼容码字与文献[6]基于AR4JA原模图构造的同等码率码长的码字性能的仿真比较。
由图7可知,在同等的码率、码长以及扩展方式的条件下,基于ARAPA原模图构造的4/5和2/3码率的码率兼容LDPC码的性能皆优于传统的基于AR4JA原模图构造的码率兼容LDPC码,仅当码率为1/2时,码率兼容ARAPA码的性能稍差于码率兼容AR4JA码。此外,这种码率兼容的ARAPA短码在误码率低至10-6时未出现错误平台,那么这种码率兼容的长码在这一误码率下亦不会出现错误平台。同时,这一仿真结果也说明了这种码率兼容ARAPA高码率码字,较传统的码率兼容AR4JA码具有较大的优势,与近年来深空通信越来越倾向采用高码率、中长码的LDPC码以满足日益剧增的数据传输这一趋势相契合。
4 结束语
本文提出了一种基于ARAPA原模图构造适用于深空通信的码率兼容LDPC码的方法。这种码率兼容的原模图LDPC码具有较低的迭代译码门限与线性的码距特性,从而更有利于较低误码平层。而且在拓展ARAPA原模图的时候,本文分两次采用PEG算法拓展的方法使得校验矩阵具有准循环特征,从而使得所得的码率兼容ARAPA码具有高速译码的特性。与传统的基于AR4JA原模图构造的码率兼容LDPC码相比,码率兼容APAPA码具有更低的译码门限值,更低的译码计算复杂度,尤其是在高码率时具有更优越的性能,可以用于越来越倾向采用高码率、中长码的LDPC码的深空通信之中以满足其日益剧增的数据传输量。
参考文献
1Orange Book.Experimental specifications,Low density parity check codes for use inNear-Earth and deep space applicationsCCSDS131.1-O-2[J].CCSDS,Sept,2007
2Gallager R G.Low-density parity-check codes [M].Cambridge.MA: M.I.T.Press,1963
3D.J.C MacKay.Good error-correcting codes based on very sparse matrices[J].IEEE Transactions on Information Theory .1999,45(2): 399-431
4Thorpe J.Low-density parity-check (LDPC)codes constructed from protographs[C]//Tech Rep ProgressReport Pasadena,CA.USA: JPL IPN,2003: 42-254
5Divsalar D,Jones C,Thorpe J.Protograph based LDPC codes with minimum distance linearly growing withblock size[C]//IEEE.IEEE Communications Societysubject.ST,louis:IEEE Globecom,2005:1152-1156
6Ha J,Kim J,McLaughlin S W .Rate-compatible puncturing of low-density parity-check codes[J].Information Theory,IEEE Transactions on,2004,50(11): 2824-2836
7Nguyen T V,Nosratinia A,Divsalar D.The design of ratecompatible protograph LDPC codes[J].Communications,IEEE Transactions on,2012,60(10): 2841-2850
8夏国江,孙辉先,熊蔚明.一族适用于空间通信的原型图LDPC码[J].兵工学报,2009,30(11):1546-1552
9Yazdani M R,Banihashemi A H.On construction of rate-compatible low-density parity-check codes[J].Communications Letters,IEEE,2004,8(3): 159-161
10Li J,Narayanan K R.Rate-compatible low density parity check codes for capacity-approaching ARQ schemes in packet data communications[C]// Communications,Internet,and Information Technology.2002: 201-206
11Liva G,Chiani M.Protograph LDPC codes design based on EXIT analysis[C]//Global Telecommunications Conference,2007.GLOBECOM’07.IEEE.IEEE,2007: 3250-3254
12Divsalar D,Dolinar S,Jones C R,et al.Capacityapproaching protograph codes[J].Selected Areas in Communications,IEEE Journal on,2009,27(6): 876-888
13Hu X Y,Eleftheriou E,Arnold D M.Regular and irregular progressive edge-growth tanner graphs[J].Information Theory,IEEE Transactions on,2005,51(1): 386-398
DOI:10.3969/j.issn.1006-6403.2016.05.010
收稿日期:(2016-03-27)
