一种新型单相并联型有源电力滤波器实现方法的研究

唐雄民， 杜芳洲， 陈思哲

(广东工业大学 自动化学院， 广东 广州 51006)



一种新型单相并联型有源电力滤波器实现方法的研究

唐雄民， 杜芳洲， 陈思哲

(广东工业大学 自动化学院， 广东 广州 51006)

摘要:提出了一种能在单相并联型有源电力滤波器(Active Power Filters, APF)中使用单闭环控制策略的实现方法.该实现方法通过构造与网侧电压、电流正交的虚拟电压、电流分量后，采用单相PQ理论推导出了单相并联型APF在理想情况下补偿电流指令的表达式.在此基础上，本文通过功率预测算法求取了用于稳定APF直流侧电压而必须从电网吸收的有功功率表达式，进而获得实际工作状态下补偿电流指令.功率预测算法的使用可使本文提出的实现方法能取消常规方法中必须具备的电压调节环节而仅采用单闭环控制策略来对APF进行控制，因而具有控制参数设定简单、系统的动态响应快和鲁棒性强等特性.文中还以实际中使用最为广泛的一种单相并联型APF的电路为例，研究了APF在启动、正常运行和负载突变状况下的动态响应过程.仿真和实验结果验证了本文提出的实现方法的有效性.

关键词:单相电路； 并联型有源电力滤波器； 补偿电流指令； 功率预测

随着社会的发展，越来越多的电力电子设备，特别是单相电力电子设备的广泛使用，严重地影响单相电网的电能质量，作为改善单相电网电能质量的单相有源滤波器的性能对改善电能质量的作用至关重要.传统的单相无源滤波器存在诸如体积大、补偿性固定、谐振等固有缺陷[1]，因此应用范围日益受限.

目前国内外对有源电力滤波的研究主要集中在三相有源电力滤波上[2-7].近年来由于对单相电网电能质量治理的关注度持续上升，对单相有源电力滤波器的研究也在逐步开展.现阶段各国学者对单相并联型APF的研究主要集中在补偿电流指令求取、主电路拓扑结构研究及系统控制策略[8-17]分析等方面.其中对补偿电流指令求取的研究最为活跃，文献[8-9]提出了基于快速傅里叶变换(FFT)的方法，但在实施过程中需要实时采集大量数据，并进行复杂的四则运算，造成补偿指令电流求取速度慢，难以满足单相APF实时工作的需求；文献[10]提出了利用正交函数的正交特性来求取补偿电流指令，这种方法速度较快，但运算电路复杂，削弱了其在实际中可操作性；对单相APF的主电路拓扑结构的研究主要集中在如何根据不同应用场合选取合适的拓扑结构上，因此国内外文献对单相全桥结构[11]、单相半桥结构[12]、级联多电平结构[13]、软开关结构[14]等不同拓扑结构都有研究，但在这些拓扑结构中，使用最为广泛的还是单相全桥结构；对控制策略的分析则主要集中在采用不同控制策略，例如单周控制[15]、重复控制[16]、滑膜控制[17]、基于李雅普诺夫方程控制[18]等，来改善单相APF的动态特性，但以上控制策略均采用传统的双环结构且都存在其固有的缺陷，如单周控制易受外界条件影响及存在功率开关管工作频率不恒定的缺陷，重复控制存在控制系统响应速度慢和控制器参数难以确定的问题，滑膜控制存在固有的抖震问题，基于李雅普洛夫方程控制存在算法实现复杂等问题.针对上述问题，本文提出了一种能在单相并联型有源电力滤波器中使用单闭环控制策略的实现方法.该实现方法采用单相PQ理论[19]和功率预测的方法获得补偿电流指令，并采用单闭环结构控制策略来对APF进行控制，具有动态响应速度快、鲁棒性好等特点，具有较好的工程应用价值.

1单相并联型APF的补偿电流指令求取

1．1单相并联型APF的工作原理

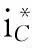
图1　单相并联型APF的工作原理图

显然，要实现APF的功能就必须满足

iC=iL-iS=iLq+∑iLh，

(1)

式(1)中：iLq为iL的基波无功电流分量；∑iLh为iL的高次谐波电流.

1．2理想状态下补偿电流指令的求取

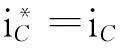
(2)

采用与式(3)相同的构造方法可得iL和iS在αβ坐标系中的表达式为

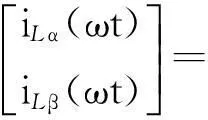
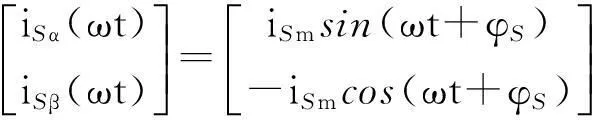
(5)

式(4)中：iLα和iLβ分别为iL在αβ坐标系中的α和β分量；iSα和iSβ分别为iS在αβ坐标系中的α和β分量；iLm为iL中的基波幅值；iSm为iS的幅值；φL和φS分别为iL的基波分量和iS与uS的相位差；in为iL中的n次谐波幅值；φn为iL中的n次谐波与uS的相位差.

仿照三相系统中瞬时有功无功的定义，可得单相电网侧和负载侧的瞬时有功无功表达式分别为

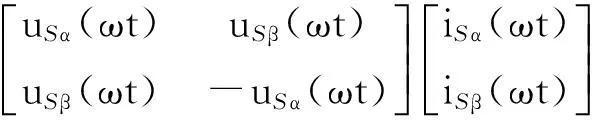
(6)

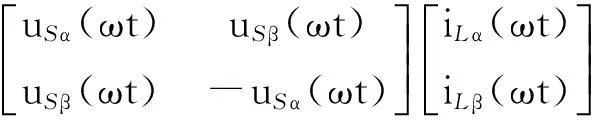
(7)

式(6)、(7)中：pS和qS分别为电网侧瞬时有功和瞬时无功功率；pL和qL分别为负载侧的瞬时有功和瞬时无功功率.

根据APF的补偿原则并考虑图1所示的参考方向，易得APF交流侧的瞬时有功功率pC和瞬时无功功率qC与 pS、qS、pL和qL的约束关系为

(8)

由于iL中含有谐波，故pL(ωt)、qL(ωt)可用直流分量和交流分量相组合的形式来描述，即

(9)

在理想情况下，APF需要补偿由于非线性负载产生的高次谐波电流和无功功率，才能确保补偿后的单相电网电流iS为标准正弦波，即

(10)

由式(8)、式(9)和式(10)可得

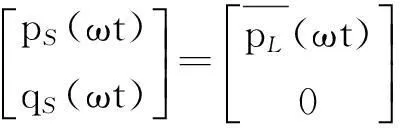
(11)

将式(11)代入式(6)，可得理想状态下iSα和iSβ的表达式为

(12)

由式(12)中的第1式可得

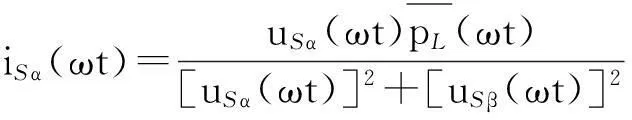
(13)

综合式(1)、式(2)、式(4)和式(13)可得理想状态下的电流补偿指令为

(14)

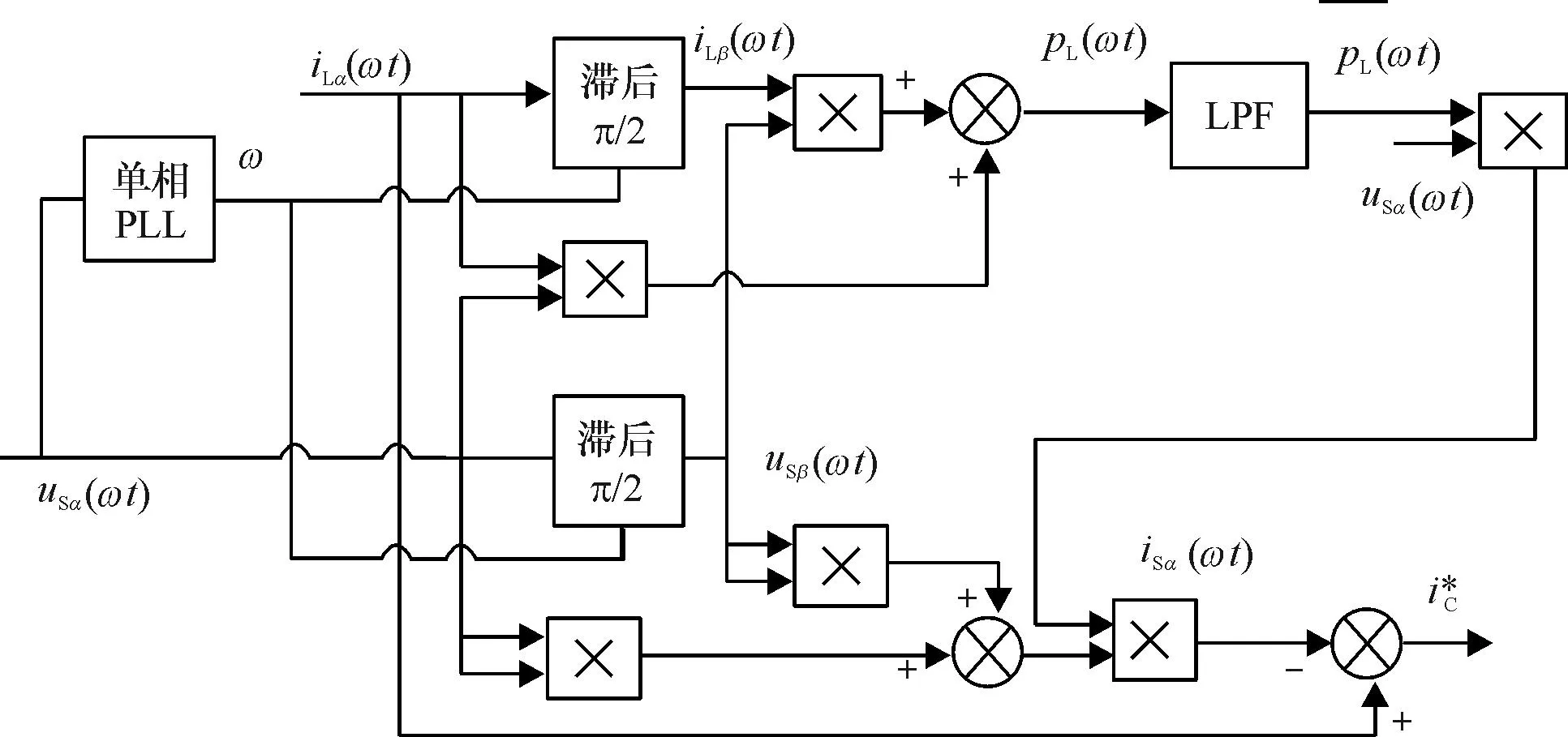
图2　理想状态下补偿电流指令求解图

1．3实际工作状态下补偿电流指令的求取

从图1中可以看出，APF输出的电流都需要由直流侧电容来提供，因此在选择合适的参考电流方向后可认为

iC=idc，

(15)

式(15)中，idc为直流侧电容输出的电流.

待APF稳定工作后，其直流侧电压udc(t)的表达式为

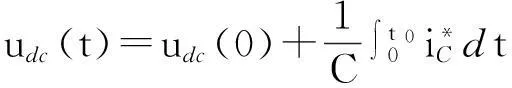
(16)

式(16)中，udc(0)为直流侧电压的初值，C为直流侧电容的容量.

由式(4)、式(7)、式(14)和式(16)可得

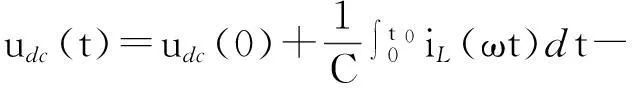
(17)

式(17)表明，在理想情况下的APF直流侧电压为一波动值，其电压波动状况与负载电流iL和电网电压uS有密切关系.但在一个完整工作周期后，直流侧电压会重新回到工作周期开始时的电压值.

考虑到在实际应用中，APF总会存在一些损耗(诸如主回路元器件热损耗和功率开关管的损耗)，使得APF必须从电网中吸收适当的有功功率，用于稳定直流侧电压.因此在实际工作状态下，还必须对式(10)进行修订，修订后式(10)变为

(18)

式(18)中：Δpdc为维持APF直流侧电压所必须从单相电网中吸收的有功功率.

由式(6)、式(8)、式(9)和式(18)，可得实际工作状态下iSα和iSβ的表达式为

(19)

综合式(1)、式(2)、式(4)和式(19)可得实际工作状态下补偿电流补偿指令为

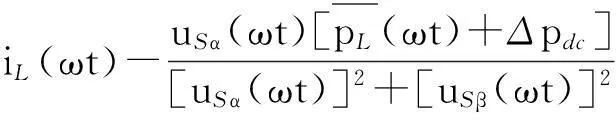
(20)

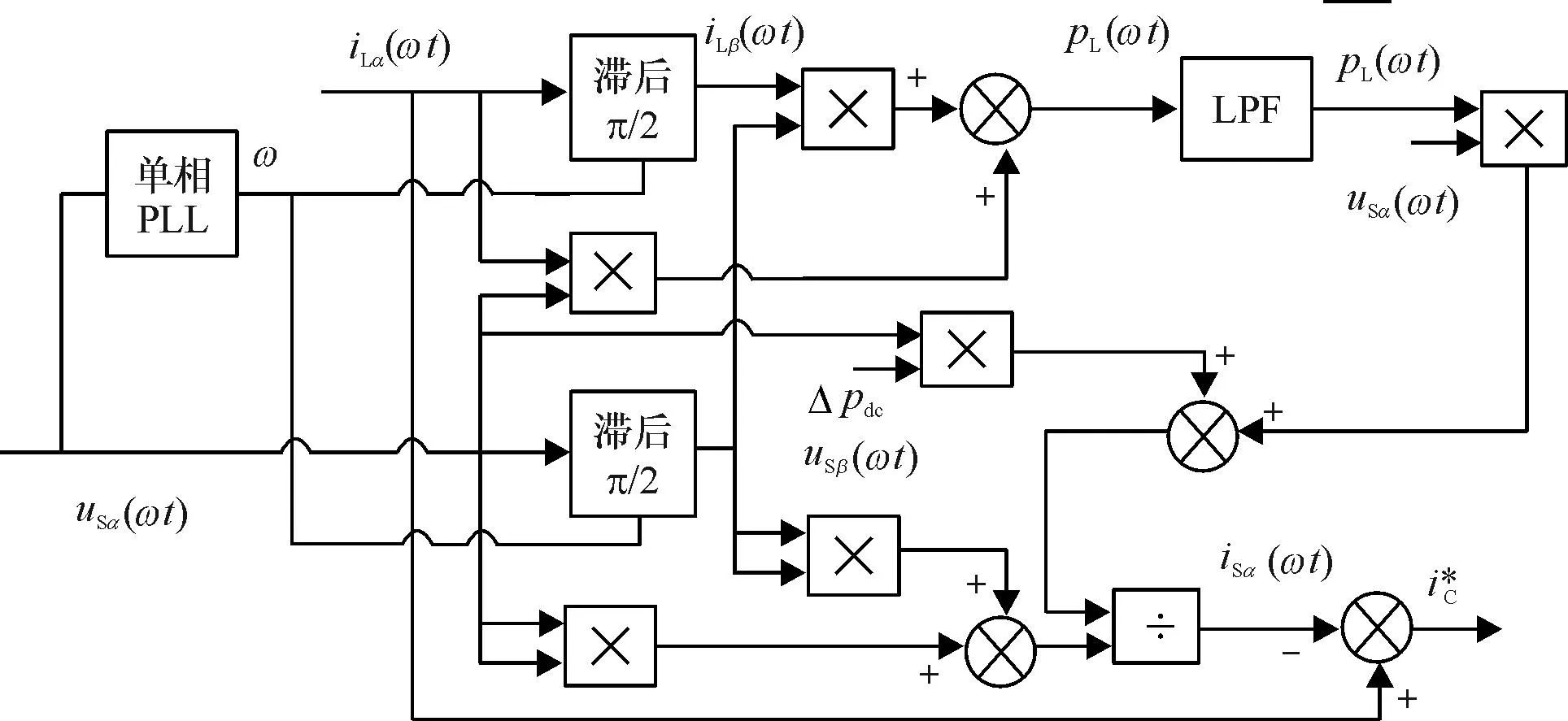
图3　实际状态下补偿电流指令求解图

采用图3所示的流程图计算得到的补偿电流指令的方法，相比文献[8-10]提出的方法具有快速性好、易于在数字控制芯片中实现等优点.

2APF吸收的有功功率求取

式(20)和图3给出了实际工作状态下补偿电流指令的求取表达式和求解流程图，但并未给出Δpdc的求解方法.这一节主要采用基于功率预测模型的方法来解决这一问题.

从前面分析可知，如不对直流侧的电压进行稳压控制，APF将丧失其功能，但考虑到APF直流侧的电压处于不断波动中(式(17))，因此，对直流侧的电压的控制实际上是对其平均值进行控制.为实现这一目的，就必须在直流电压检测环节中使用LPF环节，考虑到滤波效果和动态响应速度，LPF的截止频率一般可设置为20～30 Hz.

在一个控制周期内，直流侧电容的能量变化为

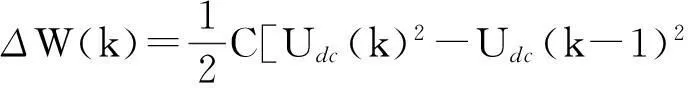
(22)

式(21)、(22)中：k-1、k和k+1为相邻的3个控制时刻；ΔW(k)、ΔW(k+1)分别为第k、k+1个控制周期内直流侧电容的能量变化；Udc(k-1)、Udc(k)和Udc(k+1)分别为k-1、k和k+1时刻udc(t)中直流侧电压经过LPF环节后的电压值.

由于在数字控制实现过程中，相邻控制周期内Δpdc的数值为一恒定值，由式(21)和(22)可得

ΔW(k+1)-ΔW(k)=Δpdc(k+1)Tk，

(23)

式中Tk为控制周期.

对式(23)进行简化可得

Δpdc(k+1)Tk.

(24)

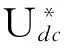
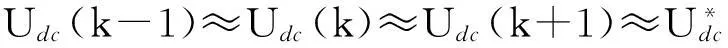
(25)

将式(25)代入式(24)可得

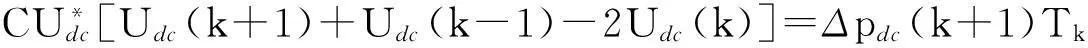
(26)

即有

Δpdc(k+1)=

(27)

或

Δpdc(k)=

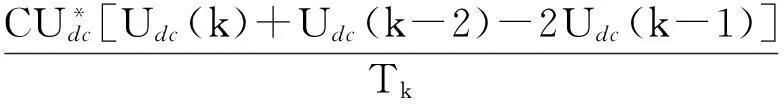
(28)

很显然，在求得控制量Δpdc(k)的基础上，就能利用式(28)和图3求取实际工作状态下补偿电流指令.

3单相并联型APF控制模型构建

图4给出了在实际中使用最为广泛的一种单相并联型APF的电路拓扑结构图.

由图4可得单相并联型APF的数学模型为

(29)

式(29)中：S1、S2分别为各桥臂的开关函数(1表示桥臂中上管导通、下管关断，0表示桥臂中下管导通、下管关断)；L为滤波电感；R为其等效电阻.

由式(20)、式(28)、式(29)和图4可得如图5所示的单相并联型APF的控制框图.

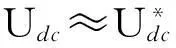
图4　单相并联型APF的电路拓扑结构图

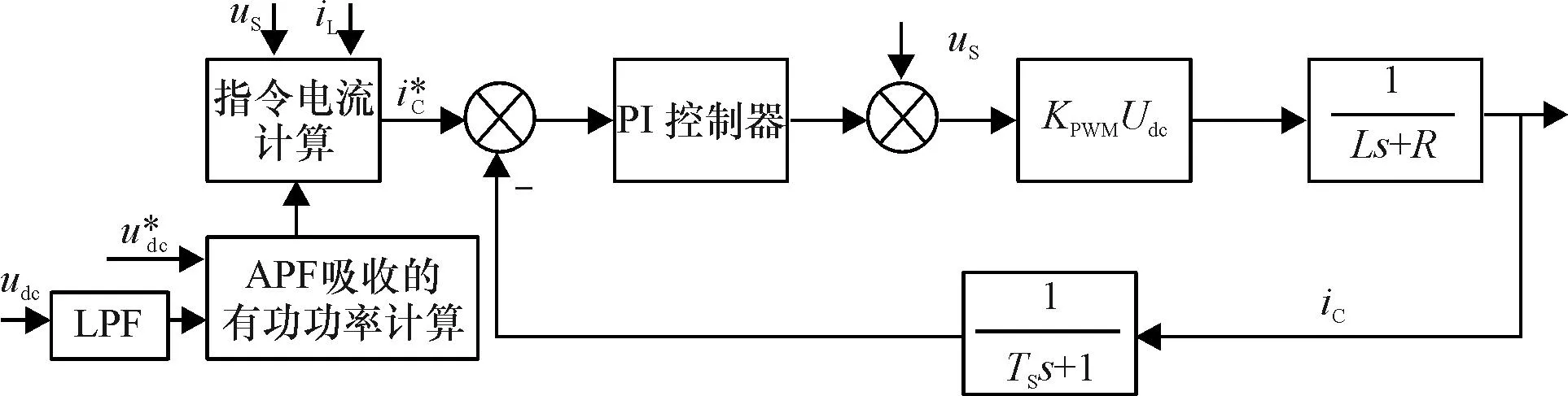
图5　单相并联型APF的控制框图

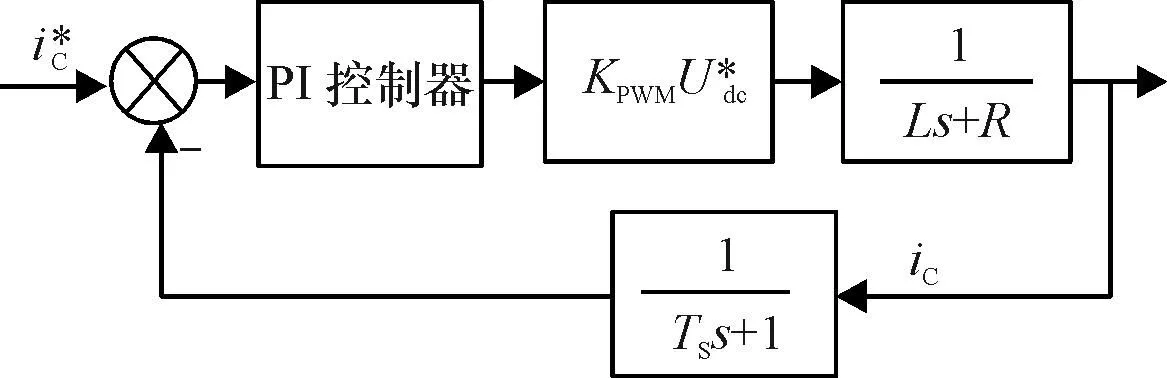
图6　单相并联型APF的简化控制框图

Fig.6The simplified control diagram of single-phase shunt APF

显然，在本文提出的控制方案中，取消了常规单相并联型APF中的所必须的电压调节环节，因而具有控制参数设定简单、动态过程短、鲁棒性好等特性.

4仿真和实验

4．1仿真结果分析

表1　APF运行的主要参数

图7、图8和图9分给出了APF补偿前后、启动过程和负载突变时的仿真波形.其中图7(a)中uS为电网侧电压，iL为流过非线性负载的电流，ih为iL中的谐波和无功电流；图7(b)、图8和9中udc为APF直流侧电压，iS为补偿后的单相电网电流，iC为APF输出的补偿电流.

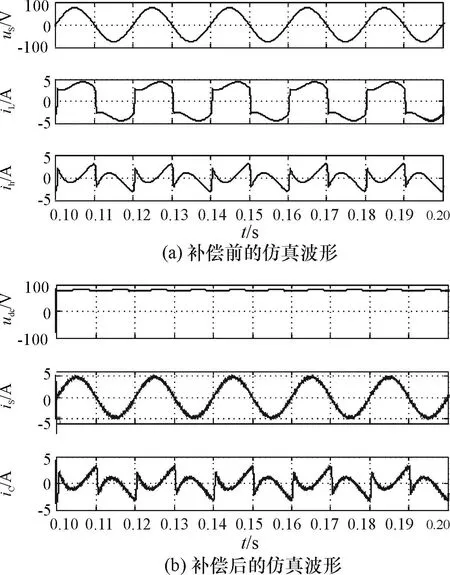
图7　APF补偿前后的仿真波形

Fig.7The simulation waveforms before and after APF compensation

图8　APF启动时仿真波形

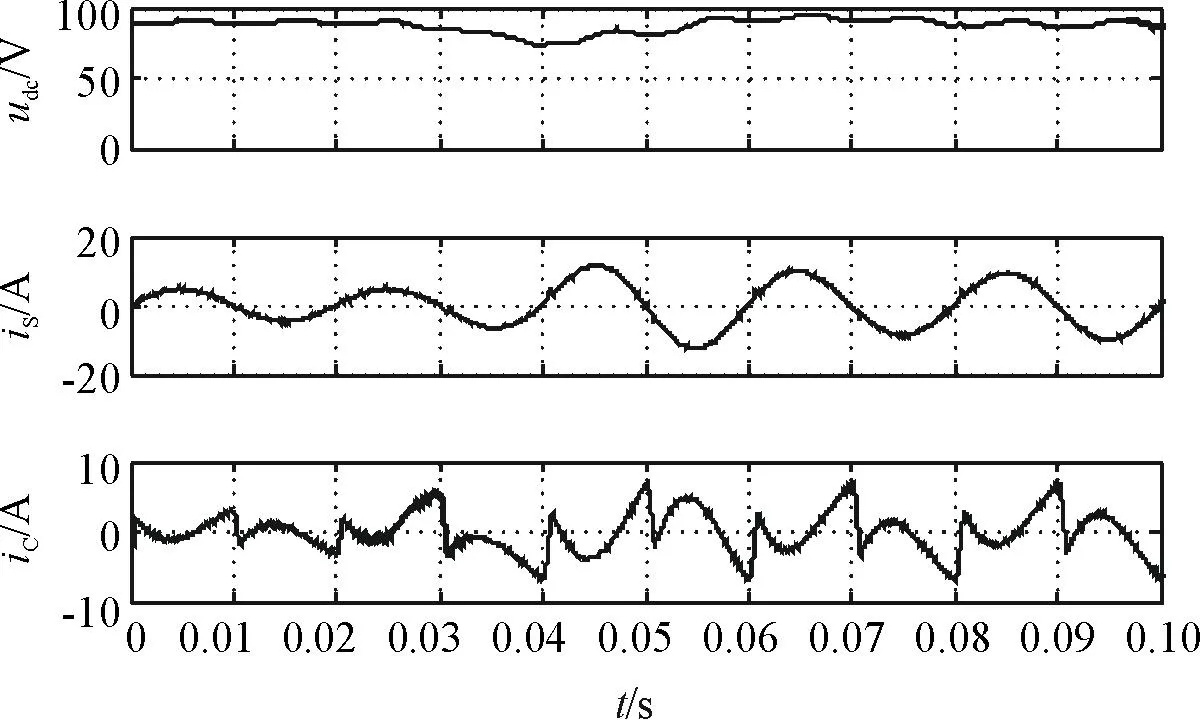
图9　负载突变仿真波形

通过对单相并联型APF的仿真图分析可知：

(1) APF输出电流iC能够很好地对负载谐波电流ih进行补偿.通过对电网电流iS补偿前后的波形进行FFT分析，iS的总谐波含量(THD)从33.41%降到4.25%，达到国家标准.

(2) 仿真运行到0.02 s时APF投入运行，系统可在1个周波内达稳定状态，表明APF具有较短的启动时间.

(3) 当非线性负载切换时(仿真运行到0.205 s时非线性负载R0由13.5 Ω切换到6 Ω)，系统能在1个周波内重新达到稳定状态，表明APF不仅对负载变化具有很好的适应性，而且具有对负载变化的快速跟踪能力.

(4) APF直流侧电压在不同工作状况下(启动、负载切换和正常工作下)都能够维持在设定值附近.

(5) 当在电网电压过零时，APF的指令电流具有最大的变化率，而PI控制规律对快速变换给定信号的跟踪始终存在一定的滞后效应，这就造成了iS在电压过零点会出现畸变(出现电流尖峰).可以预见当降低非线性负载电流的变化率时，iS在电压过零点的畸变率将大为减少.

(6) 上述分析结果验证了本文推导的补偿电流指令和提出的实现方法的有效性.

4．2实验结果分析

为进一步验证本文理论推导的正确性，笔者搭建如图10所示的实验平台，其中实验过程中采用的参数与和仿真中采用的参数一致.

系统稳定运行的实验波形如图11所示，其中图11(a)中CH1为电网电压uS，CH2为非线性负载电流iL；图11(b)中CH1为PWM驱动信号，CH2为直流侧电压udc，CH3为补偿后的电网电流iS，CH4为补偿电流iC.通过对比实验波形图11和仿真波形图7，可以发现它们之间具有高度一致性，这验证了本文提出的实现方法的可行性.需要指出的是，造成实测iS的总谐波比仿真时要稍大的原因主要有以下两点：

(1) 仿真过程中使用的单相电网电压为理想的正弦波形，而实验过程中的单相电网电压存在一定程度的畸变(图11(a)中的CH1)；

(2) 仿真中使用的功率开关模型为理想开关管，这与实际中使用的并联有吸收回路的功率开关管存在一定差异.

图10　实验平台实物图

图11　APF补偿前后实验波形

Fig.11Experimental waveforms before and after APF compensation

5结语

(1) 通过构造与网侧电压、电流正交的虚拟电压、电流分量后，采用单相PQ理论推导出了单相并联型APF在理想情况下补偿电流指令的表达式，在此基础上通过采用功率预测方法计算得到实际情况下补偿电流指令的表达式.采用这种方法求取补偿电流指令的表达式具有实时性好，准确性高的特点.

(2) 将APF的控制结构由传统控制电流和电压的双环结构变成了只需控制电流的单环结构，具有控制参数设定简单、系统的动态响应快和鲁棒性强等特性.

(3) 仿真和实验结果验证了本文提出的实现方法理论推导的正确性和实施的可行性.

参考文献：

[1] 王兆安, 杨君, 刘进军，等. 谐波抑制和无功功率补偿，2版[M]. 北京: 机械工业出版社, 2006.

[2] 许智升,陈少华,程汉湘. 消除单桥路静止无功发生器谐波的仿真[J]. 广东工业大学学报,2004,21(4): 9-14.

XU Z S, CHEN S H, CHENG H X. Eliminate single bridge STATCOM harmonic simulation[J]. Journal of Guangdong University of Technology,2004,21(4): 9-14.

[3] 罗建文, 冯垛生, 王晓毛. 基于DSP 有源电力滤波器的实验研究[J]. 广东工业大学学报, 2001,18(2): 40-43.

LUO J W, FENG D S, WANG X M. Experimental study of active power filter based on DSP[J].Journal of Guangdong University of Technology, 2001, 18(2): 40-43.

[4] CHAUHAN S K, SHAH M C, TIWARI R R, et al. Anaysis, design and digital implementation of a shunt active power filter with different schemes of reference current generation[J]. IET Power Electron, 2014, 7(3): 627-639.

[5] XIAO Z F, DENG X T, YUAN R X, et al. Shunt active power filter with enhanced dynamic performance using novel control strategy[J].IET Power Electron, 2014, 7(12): 3169-3181.

[6] 乐江源, 谢运祥, 张志, 等. 三相有源电力滤波器精确反馈线性化空间矢量PWM复合控制[J]. 中国电机工程学报, 2010, 30(15): 32-39.

LE J Y, XIE Y X, ZHANG Z, et al. Space vector PWM control of three-phase active power filter using exact feedback linearization[J]. Proceedings of the CSEE, 2010, 30(15): 32-39.

[7] TRINH Q N, LEE H H. An advanced current control strategy for three-phase shunt active power filters[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5400-5410.

[8] 薛蕙, 杨仁刚. 基于 FFT 的高精度谐波检测算法[J].中国电机工程报, 2002, 22(12): 106-110.

XUE H, YANG R G. Precise algorithms for harmonic analysis based on FFT algorithm[J]. Proceedings of the CSEE, 2002, 22(12): 106-110.

[9] 向东阳,王公宝,马伟明,等.基FFT 和神经网络的非整数次谐波检测方法[J].中国电机工程报, 2005, 25(9): 35-39.

XIANG D Y, WANG G B, MA W M, et al. A new method for non-integer harmonics measurement based on FFT algorithm and neural network[J]. Proceedings of the CSEE, 2005, 25(9): 35-39.

[10] 陆秀令, 张松华, 曹才开, 等. 单相电路谐波及无功电流新型检测方法[J].高电压技术, 2007, 33(3): 163-166.

LU X L, ZHANG S H, CAO C K, et al. New detecting method for harmonics and reactive currents in single phase circuits[J]. High Voltage Engineering, 2007, 33(3): 163-166.

[11] RAHMANI S, AL-HADDAD K, KANAAN H Y. Two PWM techniques for single-phase shunt active power filters employing a direct current control strategy[J]. IET Power Electronics, 2008, 3(1): 376-385.

[12] KOMURCUGIL H. Hysteresis current-control strategy for single-phase half-bridge shunt active power filters[C]∥2013 International Conference on Environment and Electrical Engineering (EEEIC).Wroclaw: IEEE Conference Publications, 2013:35-40.

[13] ZENG F P, TAN G H, WANG J Z, et al. Novel Single-phase five-level voltage-source inverter for the shunt active power filter[J]. IET Power Electron, 2010, 3(4): 480-489.

[14] JIANG M C, WANG C M, PERNG S S, et al. A novel single-phase soft-switching unipolar PWM shunt active power filter[C]∥ 2012 IEEE Conference on Industrial Electronics and Applications (ICIEA).Singapore: IEEE Conference Publications, 2012: 2081-2086.

[15] CHONG M Q, SMEDLEY K M, MADDALENO F. A single-phase active power filter with one-cycle control under unipolar operation[J]. IEEE Transactions On Circuits And Systems—I: Regular Papers, 2004, 8(51): 1623-1630.

[16] 张振环, 刘会金. 单相有源电力滤波器L2增益重复控制新方法[J].中国电机工程报, 2008, 28(12): 79-87.

ZHANG Z H, LIU H J. A novel L2-gain repetitive control algorithm for single-phase active power Filter[J]. Proceedings of the CSEE, 2008, 28(12): 79-87.

[17] FEI J T, ZHANG S L, ZHOU J. Adaptive harmonic compensation of shunt active power filter using sliding mode controller[C]∥ 2012 IEEE International Conference on Robotics and Biomimetics(ROBIO).Guangzhou: IEEE Conference Publications,2012:2175-2180.

[18] KOMURCUGIL H, KUKRER O. A new control strategy for single-phase shunt active power filters using Lyapunov function[J]. IEEE Transactions on Industrial Electron, 2005, 53(1): 305-312.

[19] KHADKIKAR V, CHANDRA A, SINGH B N. Generalised single-phase p-q theory for active power filtering: simulationand DSP-based experimental investigation[J]. IET Power Electron, 2009, 1(2): 67-78.

Research on a New Implementation Method for Single-Phase Shunt Active Power Filter

Tang Xiong-min, Du Fang-zhou, Chen Si-zhe

(School of Automation, Guangdong University of Technology, Guangzhou 510006, China)

Abstract:A new implementation method for single-phase shunt active power filter (APF) with single closed-loop control strategy is presented. The ideal compensation current instruction is deduced with single PQ theory, which applies with actual and virtual quartered single-phase current and voltage. Based on the ideal compensation current, the practical compensation current instruction is achieved with power predictive algorithm. Because the power predictive algorithm is adopted, the single closed-loop control strategy can be used in APF application. There is no voltage control loop in the implementation method, so the method has many favorable characteristics, such as easy designing, fast responding, strong robustness, etc. The different conditions of APF, such as startup, normal operation and load change, are also researched in the paper. The validity of implementation method for APF is proved by simulation and experimental results.

Key words:single-phase circuit; shunt active power filters; compensation current instruction; power predictive algorithm

收稿日期:2015- 12- 20

基金项目:国家自然科学基金青年基金资助项目(51207026, 51307025)；广东省自然科学基金资助项目(2015A030313487)

作者简介:唐雄民(1977-)，男，副教授，博士，主要研究方向为电力电子变流技术.

doi:10.3969/j.issn.1007- 7162.2016.03.003

中图分类号:TM714

文献标志码:A

文章编号:1007-7162(2016)03- 0011- 08