一个视网膜血管肿瘤数学模型整体解的存在唯一性

卢创业， 卫雪梅

(广东工业大学 应用数学学院，广东 广州 510520)



一个视网膜血管肿瘤数学模型整体解的存在唯一性

卢创业， 卫雪梅

(广东工业大学 应用数学学院，广东 广州 510520)

摘要:研究了一个视网膜血管肿瘤的数学模型．该模型是肿瘤生长的固定边界问题，包含了反应扩散方程和常微分方程．文中先对模型进行分类讨论，然后通过运用Banach不动点定理，抛物方程的Lp估计，证明了模型在特定情况下局部解的存在唯一性.最后利用延拓的方法得到了模型在特定情况下整体解的存在唯一性．

关键词:肿瘤生长； 整体解； 存在性； 唯一性

1问题的提出

20世纪90年代，美国科学院院士A.Friedman开始研究偏微分方程的自由边界肿瘤生长模型问题[1]．随后，一大批科研工作者开始了这个领域的研究，得到了很多出色的研究成果(见文献[2-6]及所引的参考文献)．2011年Aubert等[7]通过一个系统的五个耦合偏微分方程准确描述了一维连续介质模型的星形胶质细胞和内皮细胞的迁移．然而，这种方法无法对整个视网膜表面产生空间信息和结构细节进行刻画．建立在早先的工作，McDougall等[8]在2012年提出了一个更现实的二维混合偏微分方程的离散模型．该模型是一个持续的功能的血管实验规划模型，采用大量的实验数据再通过数值模拟计算，从而从实验角度上说明已建立的模型的实际合理性，更好地刻画了血管肿瘤的生长过程与生长规律，原模型的主要焦点是了解血管里各种相互作用的细胞、分子和代谢过程，具体模型如下：

(1)

(2)

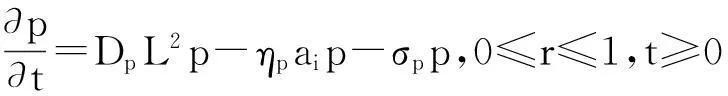
(3)

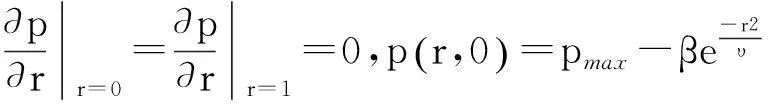
(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

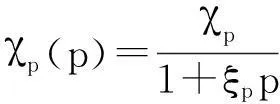
考虑到原模型存在复杂的不连续项，本文可以对上述模型分情况研究解的适定性，当ai=ni=1时，是符合医学实际的，本文将详细对该条件下的模型进行分析；当ai=ni=0时，模型将变得更加简单，其分析方法和过程与前者类同，因此本文将不再对其作详细分析.

很显然，原模型中各方程的边值均为0，初值属于Cα[0,1]，本文的主要结论如定理1.

定理1在ai=ni=1的情况下，对∀t≥0，问题(1)～(16)存在唯一解．

本文的主要结构如下：第1部分是问题及模型的介绍；第2部分先给出一些预备引理；第3部分求证模型局部解的存在唯一性；第4部分证明了此解是整体适定的，进而证得本文中的定理1.

2预备引理

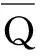
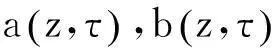
(17)

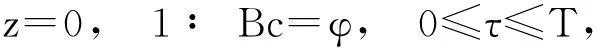
(18)

(19)

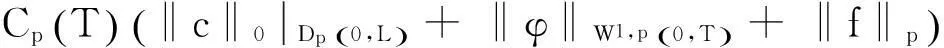
当(2)α=1，β≥0时，成立

3局部解的存在唯一性

当ai=ni=1，原模型即为

(20)

(21)

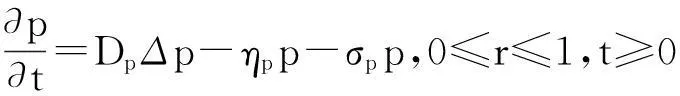
(22)

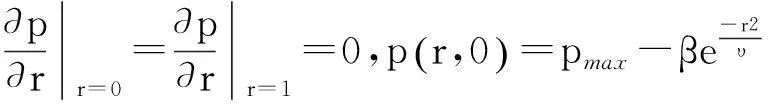
(23)

(24)

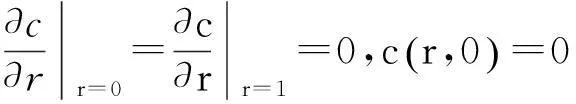
(25)

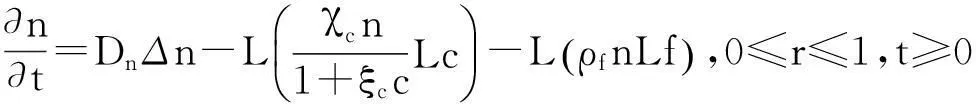
(26)

(27)

(28)

(29)

(30)

(31)

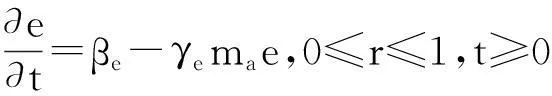
(32)

(33)

(34)

(35)

且

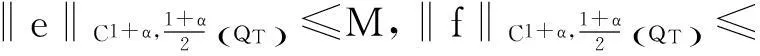
(36)

为了简便，记

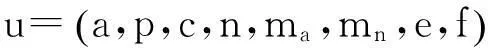
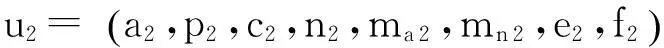
定义XM中的度量d为

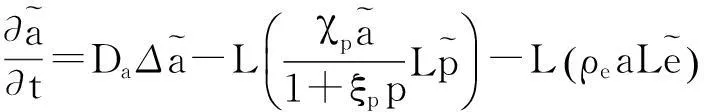
0≤r≤1,t≥0,

(37)

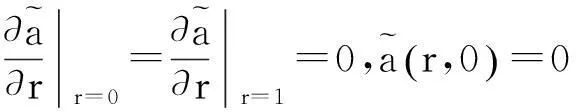
(38)

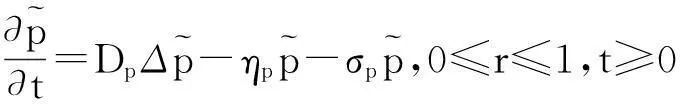
(39)

(40)

(41)

(42)

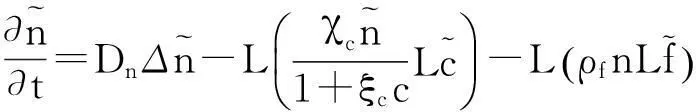
0≤r≤1,t≥0,

(43)

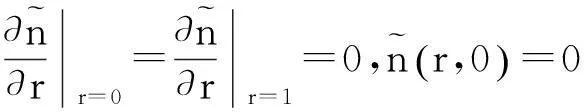
(44)

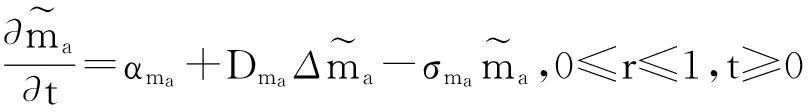
(45)

(46)

(47)

(48)

(49)

(50)

(51)

(52)

下面先证F映XM到它自身．

结合引理3可得

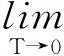
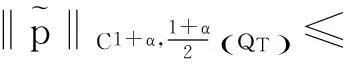
(53)

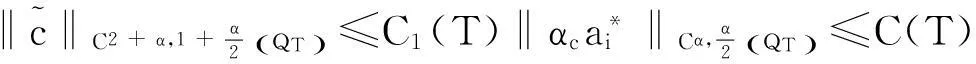
结合引理3可得

C(T)ξ(T).

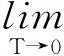
(54)

(55)

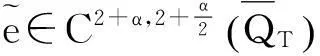
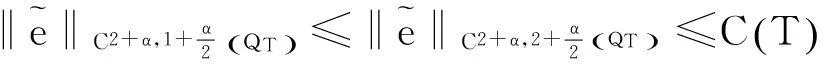
结合引理3可得

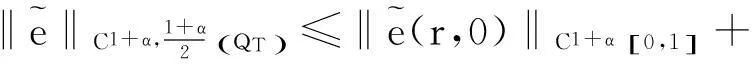
C(T)ξ(T).

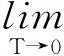
(56)

(57)

5) 问题(37)～(38)等价于以下问题：

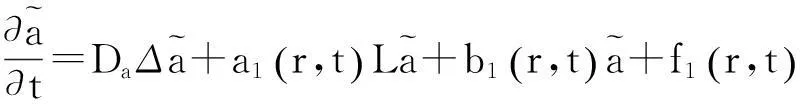
(58)

(59)

其中

(60)

(61)

(62)

(63)

结合引理3，可得

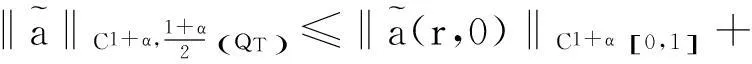
C(T，M)ξ(T).

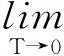
(64)

(65)

综上所述，由1)～5)可知，若取

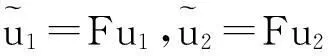
(66)

(67)

由引理2，可得

(68)

继而由引理3，可得

(69)

(70)

(71)

(72)

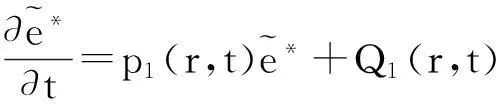
(73)

(74)

其中,

(75)

(76)

从而可得

(77)

继而由引理3，可得

(78)

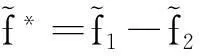
(79)

(80)

(81)

(82)

其中，

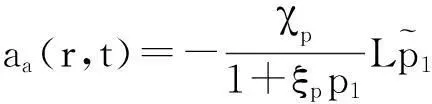
(83)

(84)

fa(r,t)=

(85)

由引理2，可得

(86)

(87)

继而由引理3，可得

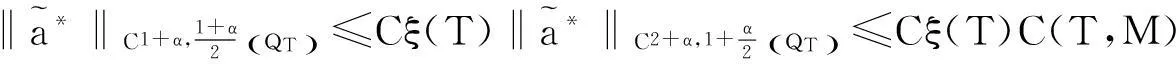
(88)

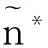
(89)

综上，由(i)～(iii)，可得

(90)

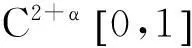
由上述结果可得到如下定理.

4整体解的存在唯一性

由上下解原理，可直接推得

引理4问题(20)～(35)的解有如下结论成立

a≥0，p≥0，c≥0，n≥0，ma≥0，mn≥0，e≥0，f≥0.

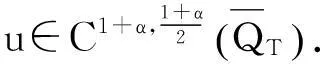
3) 考虑问题(20)～(21)，方程(21)等价于以下形式：

其中

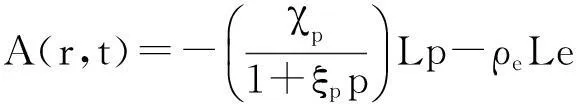
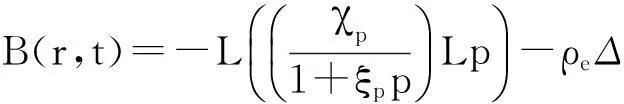
通过定理2、引理4和引理5以及时间T的任意性可证得本文的主要结论定理1．

参考文献：

[1] AVNER F，FERNANDO R．Analysis of a mathematical model for the growth of tumors[J]. Math Bio,1999, 38:262-284.

[2] CUI S B，AVNER F．Analysis of a mathematical model of the effect of inhibitors on the growth of tumors[J]. Math Bio, 2000, 164:103-107.

[3] AVNER F．Cancer models and their mathematical analysis[J].Lect Notes Math, 2006, 1872:223-246.

[4] AVNER F．Mathematical analysis and challenges arising from models of tumor growth[J].Math Models Appl Sci, 2007, 17:1751-1771.

[5] 崔尚斌．肿瘤生长的自由边界问题[J].数学进展(中),2009,38(1):1-18.

CUI S B．Free boundary problem of tumor growth[J].Advances In Mathematics,2009,38(1):1-18.

[6] WEI X M．Global Existence for a Free Boundary Problem Modeling the Growth of Necrotic Tumors in the Presence of Inhibitors[J]. Inter Pure Appl Math, 2006,28(3):321-338.

[7] AUBERT M，CHAPLAIN M A J，UGALL S R．A continuous mathematical model of the developing murine retinal vasculature[J].Bull Math Biol,2011, 73:2430-2451.

[8] MCDOUGALL S R，WATSON M G，DEVLIN A H，et al．A hybrid discrete-continuum mathematical model of pattern prediction in the developing retinal[J].Bull Math Biol,2012, 74:2272- 2314.

[9] AVNER F，GEORGIOS L．Analysis of a mathematical model of tumor lymphangiogensis[J].Math Models Appl Sci, 2005, 15:95-107.

[10] 王术．Sobolev 空间与偏微分方程引论[M].北京：科学出版社,2009:58-64.

[11] WEI X M，CUI S B．Existence and uniqueness of global solutions for a mathematical model of antiangiogenesis in tumor growth[J].Nonlinear Anal-Real, 2007(9):1827- 1836.

Existence and Uniqueness of Global Solution to a Mathematical Model of Retinal Vascular Tumors

Lu Chuang-ye,Wei Xue-mei

(School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China)

Abstract:In this paper the researchers study a mathematical model of a retinal vascular tumor. The model is a fixed boundary problem of tumor growth, including several reaction diffusion equations and ordinary differential equations. The paper first discusses the classification of the model, then applies Lp-estimate and Banach Fixed Point Theorem to prove the existence and uniqueness of local solution under special conditions. In the end, the local solution proves to be global in special cases by continuation method.

Key words:tumor growth; global solution; existence; uniqueness

收稿日期:2015- 05- 20

基金项目:国家自然科学基金资助项目(11101095);广东省高层次人才项目(2014011)

作者简介:卢创业(1990-)，男,硕士研究生，主要研究方向为偏微分方程.通信作者: 卫雪梅，女，教授，主要研究方向为偏微分方程. E-mail：wxm_gdut@163.com

doi:10.3969/j.issn.1007- 7162.2016.03.013

中图分类号:O175

文献标志码:A

文章编号:1007-7162(2016)03- 0070- 06