自适应步长神经网络盲分离算法的研究与应用

杨硕，刘小斌，杨建青

(1.甘肃农业大学工学院，甘肃 兰州　730070；2.兰州工业学院汽车工程学院，甘肃 兰州；730050)



自适应步长神经网络盲分离算法的研究与应用

杨硕1，刘小斌2，杨建青1

(1.甘肃农业大学工学院，甘肃 兰州730070；2.兰州工业学院汽车工程学院，甘肃 兰州；730050)

摘要：【目的】利用神经网络盲分离算法来解决含噪声音信号盲分离问题.【方法】提出了一种改进的自适应步长混合神经网络算法，该算法可以很好的掌控步长因子函数的形状，且在接近零点处步长变化缓慢，使性能更加优越；同时针对神经网络结构的不足引入了递归结构，通过与改进的自适应步长算法的结合达到更好的分离效果.【结果】通过在汽车发动机含噪声音信号中的应用，表明出该算法稳定性、收敛性好，可灵活的控制了步长因子分离出发动机噪声信号，达到较好的分离效果.

关键词：盲分离；神经网络；自适应步长

基于盲分离理论对含噪声音信号去噪方法的研究引起了人们的极大关注.Lee等[1]提出了通过神经网络进行独立分量分析(independent component analysis，ICA)方法，在这基础上其他研究者分别提出了联合对角化算法，自然梯度算法，基于固定点快速迭代算法(FastICA)[2-4].综上所述的方法在生物医学、图像处理、电路测试等领域有着广泛的应用，但针对含噪声音信号盲分离的问题上，上述算法的优势性能则会下降，不能达到预期分离效果.Hyvarinen等和Cichocki等[5-6]分别提出了联合最大似然估计法、基于累积量的方法来解决含噪声音信号盲分离的问题，但这2种方法运算繁琐，收敛速率慢，并且存在一定的误差，影响了盲分离的效果，本文针对上述算法存在的缺陷提出了一种改进的步长自适应神经网络盲分离算法，其算法既能减小误差还可以灵活控制步长因子，提高了收敛速率.在改进算法的基础上，又将递归结构引入其算法，这样可使收敛速度更快，达到更好的分离效果.

1研究内容与方法

为了能更好的将含噪声音信号进行分离，把整个分离过程分为2个层次，第1层为白化处理，第2层利用改进的步长自适应混合神经网络盲分离算法将白化信号进行分离.

1.1神经网络盲分离数学模型

首先建立神经网络的数学模型，设m个独立的声源信号s(t)=[s1(t),…,sn(t)]T，经过噪声n(t)=[n1(t),n2(t),…,nm(t)]T混合，经传感器接受得到n个观测信号x(t)=[x1(t),…,xm(t)]T，n≥m，其数学表达式如下：

x(t)=A[s(t)+n(t)]

(1)

(2)

1.2白化处理

W(t)=W0X(t)

(3)

(4)

2神经网络盲分离算法的改进

2.1基于最小互信息的神经网络盲分离算法

经过白化处理后，基于神经网络盲分离原理将含噪声音信号看做多输入多输出的混合系统，其原理图如图1所示.

图1　神经网络盲分离原理 Fig.1　The principle diagram of the neural blind source separation

通过神经网络原理图可以将盲分离问题转变成求逆神经网络系统，使得估计信号为

y(t)=[y1(t),y2(t)，…,yn(t)]T=Wx(t)

=WAs(t)=s(t)

(5)

其中W=[wij(t)](i=1,2,…,n;j=1,2,…,n)为权值矩阵.再利用联合概率密度和边缘概率密度乘积的KL( Kullback-Leibler)散度计算I(y):

(6)

对联合概率密度py(y)与各分信号边缘概率密度py(yi)存在的函数求导可知I(y)≥0，利用ICA的理论可以得出最小互信息的盲信号处理算法：

(7)

=-(W-T-f(y)xT)

(8)

其中：

f(y)=[f1(y1),f2(y2),…,fn(yn)]T

(9)

=W(t)+μ[I-f(y)yT]W(t)

(10)

其中μ为学习步长.

2.2自适应步长神经网络盲分离算法

对于学习步长μ影响分离效果来说，减少步长因子则能提高算法收敛精度，反之则加快收敛速度与跟踪速度[8].对于神经网络算法的收敛精度、收敛速度、跟踪速度方面学习步长存在一定的矛盾.为了解决这一矛盾，覃景繁等[9]提出了基于Sigmoid函数的变步长LMS算法：

(11)

该算法既可以获得获得较快的收敛速度和跟踪速度也可以获得较小的稳态误差，但是在误差函数接近零处不具有缓慢变化的特性，使得该算法在稳态阶段仍有较大补偿变化[4].因此，本文提出了一种新的调整步长的函数：

(12)

其中，k,α>0并且可以控制μ(t)的形状，β控制了μ(t)的取值范围.

图2为改进自适应步长函数在不同参数下的曲线图，μ(t)为纵坐标，e(t)为横坐标.图2-A在α=5，β=1的情况下，SVSLMS算法与本文改进自适应算法的对比曲线，经过对比可以看出SVSLMS算法稳定性失调，而改进后的算法在接近零点处具有更好的稳定性.图2-B-D分别为γ、α、β取不同值时本文自适应算法的步长因子曲线.从图(2)的仿真可以看出，本文的改进算法比SVSLMS算法的稳定性更好且能灵活控制.由于该算法要应用在含噪声音信号中，含噪声音信号及误差函数未知，所以要找一个替代函数.因此，改进的自适应步长算法具体步骤如下，首先进行离散余弦变换：

Xdct(t)=DCT[X(t)]

(13)

其中，DCT[X(t)]为离散傅里叶变换函数.

当式(10)中[I-f(y)yT]趋近于零，收敛变化与于误差变化特性相近，则误差信号为：

(14)

W(t+1)=W(t)+2μ(t)e(t)D-1Xdct(t)

(15)

2.3步长自适应混合神经网络盲分离算法

虽然利用步长自适应算法可以减小误差，并可控制步长因子提高收敛速度，较好的分离信号，但收敛速度仍不够理想.本文将引用递归网络，并利用本文改进算法来控制两种算法的学习步长，其原理如图3.

图2　改进自适应步长因子函数性能Fig.2　Improving the performance of adaptive step length factor function

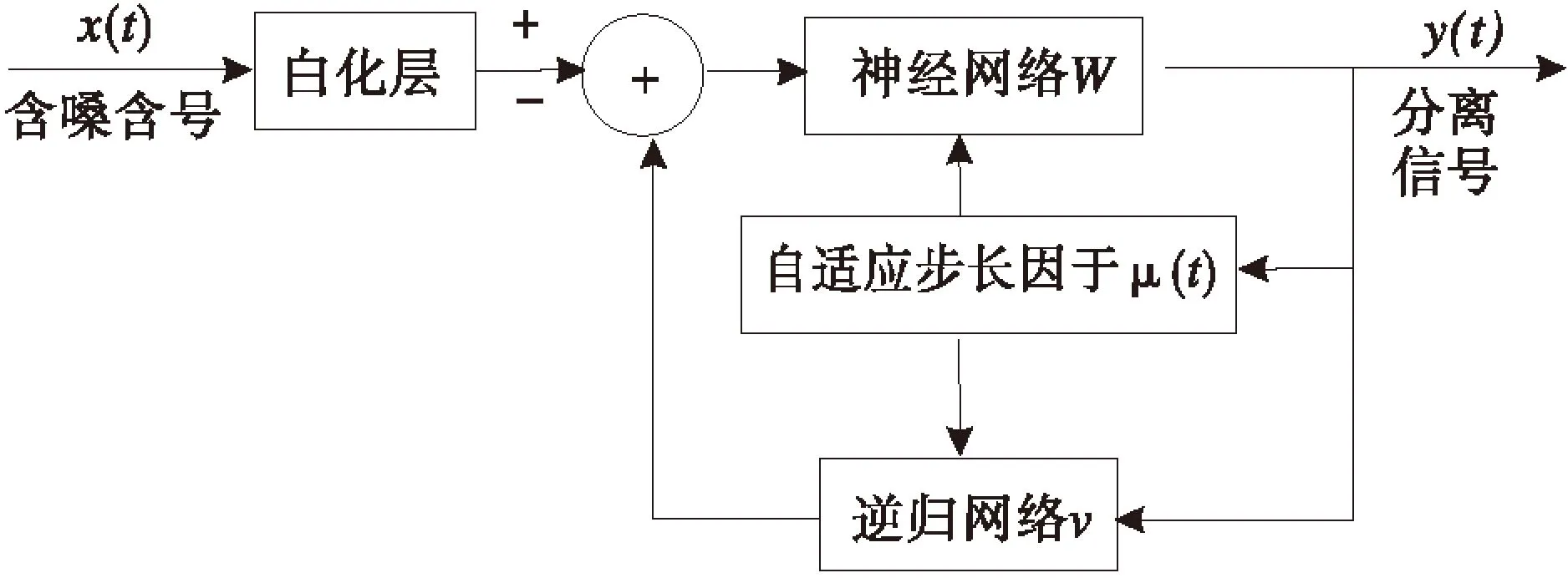
图3　自适应步长混合神经网络盲分离原理Fig.3　The adaptive step length hybrid neural network blind separation principle

由图3可知，含噪声音信号为：

y(t)=W[x(t)-Vy(t)]=Wx(t)-WVy(t)

(16)

递归网络权值矩阵V=[vij](i=1,2,…,n；j=1,2，…,n)，且vij≠0(1,2，…，n).由自然梯度原理可知，递归网络权值可改写为：

W(t+1)=W(t)+ΔW(t)

=W(t)+μ(t)[I-f(y)yT]W(t)

(17)

因此，求递归神经网络权值矩阵的计算方法如下：根据Jutten和 Hérault提出的递归神经网络结构示意图(图4)，可得出y(t)=x(t)-Vy(t)，即y(t)=[I+V]-1x(t).

图4　递归神经网络盲分离原理Fig.4　The principle diagram of the recursive neural network blind source sseparation

利用自然梯度算法得出，ΔV=-u(t)[I+V(t)][I-f(y)yT]，因此，该混合神经网络结构权值矩阵可改写为：

V(t+1)=V(t)+ΔV(t)

=V(t)-μ(t)[I+V(t)][I-f(y)yT]

(18)

其中式(15)(16)的步长因子μ(t)由式(11)确定，且可以得到新结构的全局矩阵：

C=(I+WV)WA

(19)

3改进算法在汽车发动机故障诊断中的应用

本文将对汽车发动机发生故障时的含噪声音信号作为试验数据.选取五菱宏光为被测汽车，发动机型号LMU，4气缸，最大功率63kW，最大功率转速6 000r/min.首先将被测发动机放在一个绝对安静的房间里，人为设置使一个气缸不工作，将传感器放在距离被测发动机0.1m处进行声音采集，然后再次对气缸不工作时的情况进行声音采集，但在采集过程中人为增添一些频率、大小接近气缸不工作时发动机的声音，并作为分离信号，选取前1 200个采样点作为源信号，步长因子按式(13)计算，选取β=0.1，α=10，γ=1，初始值μ(0)=0.01，分析可知自适应步长取值范围为[0,10]，曲线图与图2-cα=10时相同，由图2-c可明显的看出，当e(t)的取值接近零时步长因子变化稳定，当e(t)增大时，步长因子变化幅度增大，进而收敛速度较快.而步长取值范围为[10,∞]当时数值越大时，收敛性越不稳定，因为收敛性代表着分离效果，意味着最终的分离效果不佳.通过多次实验步长取值范围在[0,10]时，改进算法对本试验分离效果最佳，达到对汽车故障诊断的实验目的.图5-8分别为含噪故障发动机声音信号、自适应步长算法分离噪声后的信号、改进的自适应步长混合神经网络算法分离噪声后的信号以及故障发动机声音信号.通过图6-8的对比可明显的看出自适应步长算法已经有了明显的分离效果，但改进的自适应步长混合神经网络算法分离效果更好，体现出其方法去噪分离的优越性，通过对图7与图8的波形对比，经过去噪后的波形与故障发动机声音信号波形相似，对故障发动机的检测提供了较好的判断.

图5　故障发动机含噪声音信号Fig.5　The fault of engine noise signals

图6　自适应步长算法分离噪声后的信号Fig.6　The adaptive step length after algorithm to separate the noise signal

图7　改进的自适应步长混合神经网络算法分离噪声后的信号Fig.7　The improved adaptive step length after the hybrid neural network algorithm to separate the noise signal

图8　故障发动机声音信号Fig.8　The fault engine sound signals

为了进一步展示改进算法的分离效果，图9显示了3种算法下曲线收敛的情况.从收敛速度上看，固定步长神经网络在240步左右收敛，自适应步长神经网络提高到100步左右收敛，而改进的自适应步长混合神经网络则在20步左右就达到稳定，收敛速度极快，因为收敛程度也就代表了分离效果，所以很明显的看出改进的自适应步长混合神经网络分离效果最佳.

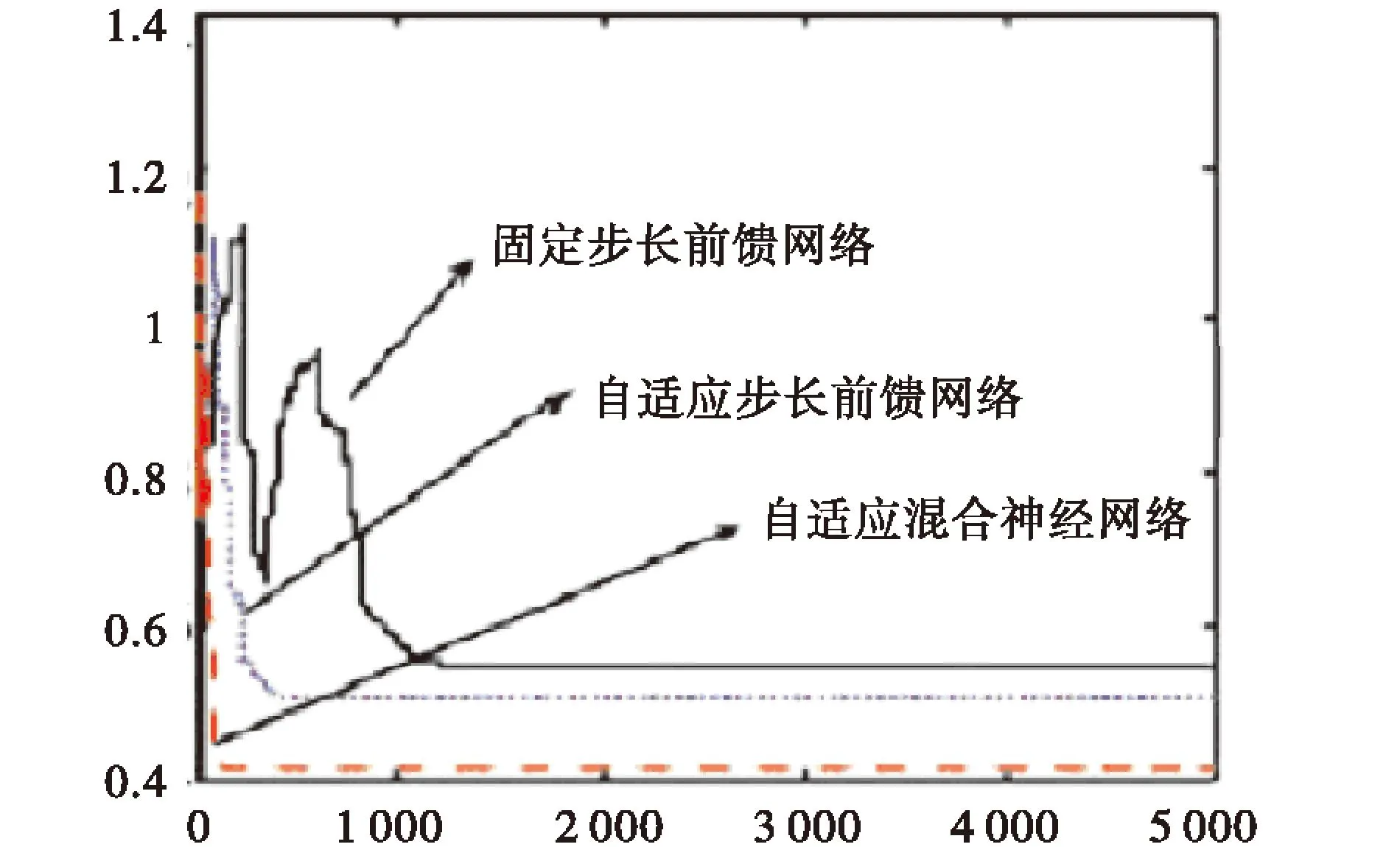
图9　3种算法收敛速度比较Fig.9　The kinds of algorithm convergence speed

4结论

本文针对传统的神经网络算法中步长固定的不足提出了一种改进的自适应步长混合神经网络算法，该算法可灵活的控制步长因子，达到更快的收敛速度.通过试验仿真，改进算法收敛性能好，对分离含噪声音信号的效果优越，在对汽车发动机故障检测的应用起到了很好的效果.但在改进算法中，对于不同的试验数据的步长因子取值范围不同且必须在一个固定的取值范围内其算法才可以有效应用.因此，为了能不受步长因子取值范围的影响使算法在其它领域中可进行应用，此算法还有待改进和完善.

参考文献

[1]Lee T W.Independent component analysis using an extended informax algorithm for mixed subgaussion and supergaussion sources[J].Neural Computation,1999,11(20):417-441

[2]叶重元，黄永东.小波阈值去噪算法的新改进[J].计算机工程与应用,2011,47(12):141-145

[3]任婕.含噪盲信号提取和分离技术研究[D].成都：电子科技大学，2012

[4]Hyvarinen A.Survey on independent component analysis[J].Neural Computing,1999,2(1):942-948

[5]Hyvarinen A.Gaussian moments for noisy independent compon- ent analysis[J].IEEE Signal Processing Letters,1990,6(6):145-147

[6]Cichocki A,Amari S.Adaptive blind signal and image processing-learning algorithms and applications[M].U S A：John Wiley & Sons Inc,2002

[7]张敬春，谷爱昱，王战盟，等.基于盲分离的电机故障诊断[J].电力系统及其自动化学报,2006,18(4):67-70

[8]赵来娟，张仁陟，陈映江，等.远程控制精准化灌溉系统中自适应均衡技术仿真研究[J].甘肃农业大学学报,2011,46(1):156-160

[9]覃景繁，韦岗.基于s型函数的变步长LMS自适应滤波算法[J].无线电工程,1996,26(4):44-47

[10]孙娟，王俊，刘斌.基于相对误差互相关函数的变步长LMS算法[J].系统工程与电子技术,2008,30(12):2316-2320

[11]吕淑平,方兴杰.基于独立分量分析的自适应在线算法[J].计算机应用研究,2010,27(11):4140-4145

[12]Ichocki A，Unbehauen R.Robust neural networks with on-line learning for blind identification and blind separation of sources[J].IEEE Trans on Circuit and Systems I:Fundamental Theory and Applications,1996,43(11):894-906

[13]Cruces S,Castedo L,Cickocki A.Robust blind source separa-tion algorithms using cumulates[J].Neurocomputing,2002,49(1):87-118

[14]王宇，迟毅林，伍星，等.基于盲信号处理的机械噪声监测与故障诊断[J].振动与冲击,2009,28(6):32-41

[15]牛亮，马建仓.一种新的基于峰度的盲源分离开关算法[J].系统仿真学报,2005,17(1):125-188

[16]余华，吴文全，刘忠.自适应步长EASI算法研究及改进[J].舰船电子工程,2009,28(4):118-120

[17]张洪渊，贾鹏，史习智，等.确定盲分离中未知信号源个数的奇异值分解法[J].上海交通大学学报,2001,35(8):1155-1158

[18]丛丰裕，雷菊阳，许海翔，等.在线增强型复值混合信号盲分离算法研究[J].西安交通大学学报,2006,40(9):1070-1073

(责任编辑李辛)

Research and application of blind source separation algorithm of adaptative-step-size neural network

YANG Shuo1,LIU Xiao-bin2,YANG Jian-qing1

(1.College of Engineering,Gansu Agricultural University,Lanzhou 730070,China;2.College of Automotive Engineering,Lanzhou Institute of Technology,Lanzhou 730050,China)

Abstract：【Objective】 Blind source separation algorithm based on neural network was used to solve the problem of blind source separation of sound signal including noise.【Method】 An improved adaptive-step-size compound neural network algorithm was proposed,which can well control the shape of the step size factor function,the step size changed slowly near the zero making the performance more superior.At the same time,recursive structure was introduced aiming at the shortcomings of the neural network structure,which was combined with the improved adaptive step size algorithm to achieve better separating effect.【Result】 Application of the algorithm in automobile engine including noise signal showed good stability and convergence and it could control flexibly the step factor and separate engine noise signal achieving good separating effect.

Key words：blind source separation;neural network;self-adaptive step size

通信作者：刘小斌，男，教授，主要从事嵌入式系统开发、机电控制与系统仿真方面的教学与研究工作.E-mail:LZGZ_LXB@163.com

收稿日期：2015-04-07；修回日期：2015-04-27

中图分类号：TP 301.6

文献标志码：A

文章编号：1003-4315(2016)02-0155-06

第一作者：杨硕(1988-)，男，硕士研究生，主要从事电气化与信息化方向的研究.E-mail:273449921@qq.com