倒Y型挡土墙结构的抗滑稳定性

施小平

(合肥工业大学 资源与环境工程学院, 安徽 合肥 230009)



倒Y型挡土墙结构的抗滑稳定性

施小平

(合肥工业大学 资源与环境工程学院, 安徽 合肥 230009)

[摘要]【目的】 研究倒Y型挡土墙结构的稳定性，为填土范围较小、施工空间有限、地基开挖难度较大区域倒Y型挡土墙的设计提供参考。【方法】 基于非线性有限元法，对倒Y型挡土墙结构的设计参数进行对比分析，确定其最优值。【结果】 对比计算结果表明，倒Y型挡土墙墙趾板长度每增加0.5 m其安全系数可提高3.5%，墙趾板与铅垂线夹角每增加10°其安全系数可提高2.73%，墙踵板长度每增加0.5 m其安全系数可提高4.35%；倒Y型挡土墙的安全系数随着墙踵板与铅垂线夹角的增大而呈现出先增大后减小的趋势。【结论】 倒Y型挡土墙墙趾板与铅垂线夹角为90°、墙踵板与铅垂线夹角45°时，挡土墙的稳定性最高。挡土墙的稳定性随墙趾板、墙踵板长度的增加而提高，但墙趾板、墙踵板的具体长度应根据具体地质条件及稳定性要求计算确定。传统悬臂式挡土墙也可视为倒Y型挡土墙的一个特例。

[关键词]倒Y型挡土墙；抗滑稳定性；滑裂面；墙趾板；墙踵板

挡土墙是指支承路基填土或山坡土体，防止其变形失稳的构造物，在土木建筑、水利水电、铁道交通等工程建设中应用广泛[1-3]。

在一些石料来源丰富的地区，石砌的重力式挡土墙因就地取材方便、施工方法简单而成为我国广泛使用的支档结构。但随着经济的不断发展，岩土工程对节能、环保提出了更高的要求。挡土墙结构已由单纯依靠自重来抵抗墙后土压力的支护方式，发展为采用支撑、锚固及加筋复合结构的多种新型支档结构[4-6]。

在某些特殊地段，为了满足某些特殊附加功能及要求，可以设计出一些特殊的、不常见的挡土墙类型[7-8]。在填土范围较小、施工空间有限，或地基开挖难度较大的岩石、碎石山区，为减小挡土墙基础开挖工程量且有效利用较高的地基承载力，可采用倒Y型挡土墙结构[9]，其一般仅需开挖墙踵板位置处的山体，工程开挖量较小。倒Y型挡土墙类似于“壳体”基础，能将土压力扩散到较大的土层中去，一般多采用钢筋混凝土浇筑而成。

本研究基于非线性有限元法，对倒Y型挡土墙结构的设计参数进行了对比分析，以期得到其稳定性变化规律，进而提出最优设计形式，为倒Y型挡土墙结构在工程中的应用提供参考。

1有限元计算模型

一般而言，倒Y型挡土墙结构(图1)的立臂高度由现场地形地势决定，取值变化性不强，而墙趾板、墙踵板的长度及与铅垂线的夹角则可以灵活组合变化，其是倒Y型挡土墙结构的重要设计参数。

图 1　倒Y型挡土墙的结构

建立如图2所示的计算模型，墙趾板的长度及其与铅垂线的夹角分别为L1、β1，墙踵板的长度及与铅垂线的夹角分别为L2、β2，此4个参数即为倒Y型挡土墙设计过程中需要确定的重要参数。挡土墙后为填土，填土高度4.0 m；挡土墙立臂、墙趾板及墙踵板的厚度均为0.50 m；挡土墙置于地基土上，其中地基土Ⅰ厚2 m,地基土Ⅱ厚4 m，地基土III厚5 m。将挡土墙按平面应变问题考虑，地基土与填土材料的本构模型采用莫尔-库仑理想弹塑性模型，挡土墙为钢筋混凝土结构，其强度较高，可按线弹性材料考虑，土层及结构物的计算参数见表1。

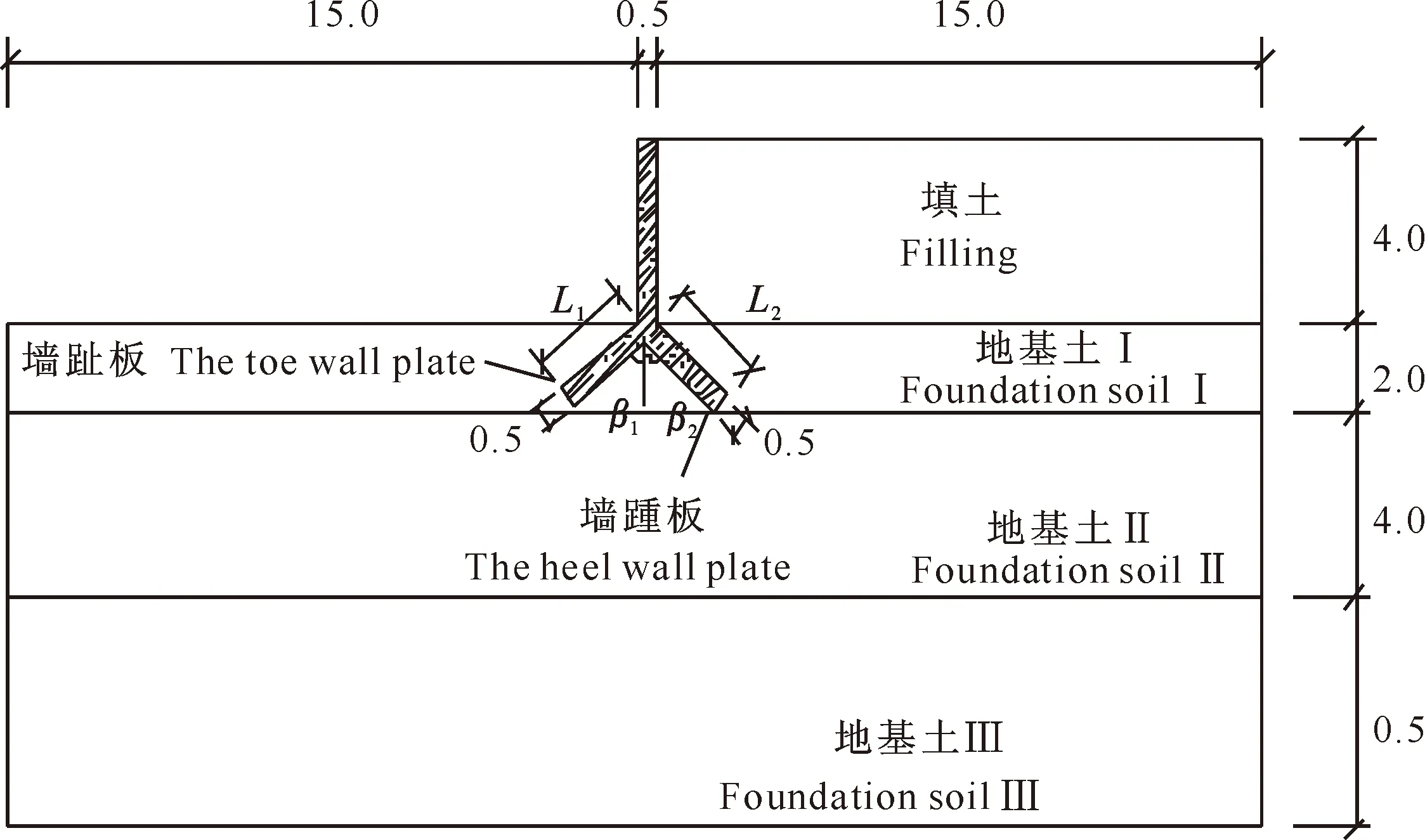
图 2　倒Y型挡土墙的几何断面构型(单位:m)

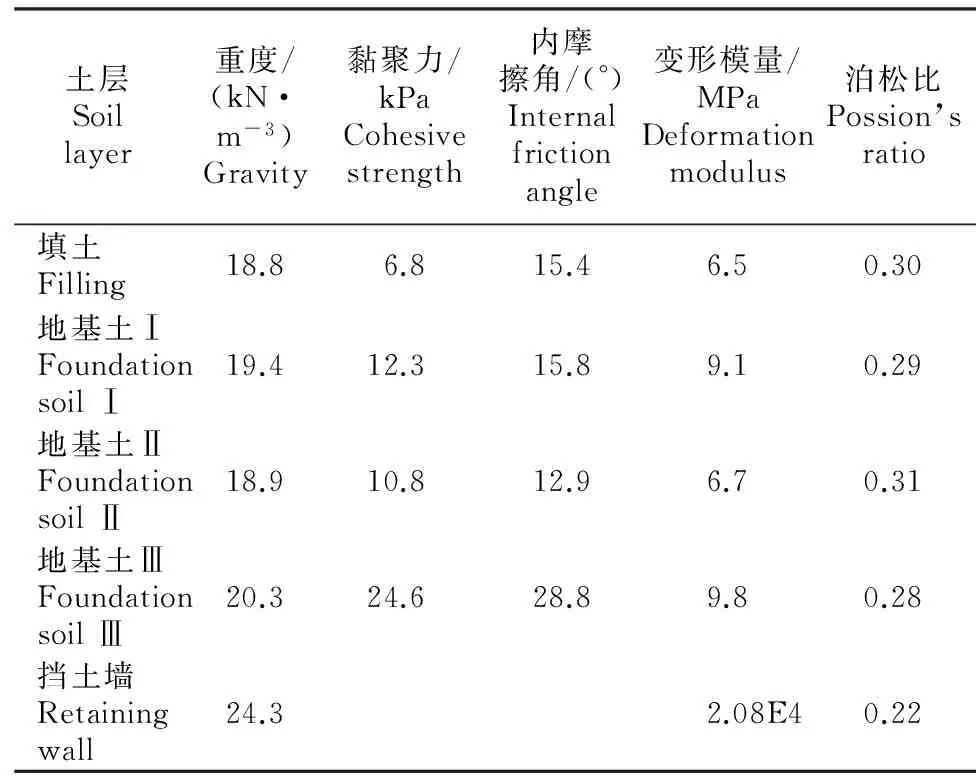
土层Soillayer重度/(kN·m-3)Gravity黏聚力/kPaCohesivestrength内摩擦角/(°)Internalfrictionangle变形模量/MPaDeformationmodulus泊松比Possion’sratio填土Filling18.86.815.46.50.30地基土ⅠFoundationsoilⅠ19.412.315.89.10.29地基土ⅡFoundationsoilⅡ18.910.812.96.70.31地基土ⅢFoundationsoilⅢ20.324.628.89.80.28挡土墙Retainingwall24.32.08E40.22

挡土墙与土体之间的摩擦通过设置接触面单元来实现，采用参数Rinter来反映两者相互作用的程度，Rinter=[0,1.0]。参考文献[10]，并结合墙后土体的物理力学参数，本次计算中取Rinter=0.68。

有限元计算域应足够大，以便消除边界条件对计算结果的影响。有限元计算的边界条件为：底部采用固定边界条件，即水平和竖向均不发生位移，两侧为水平方向位移约束条件。采用15节点的三角形单元对计算模型进行网格划分，图3给出了挡土墙有限元网格的划分情况，网格单元共1 288个。

一般地，挡土墙常先于填土施工，故可认为在填土施工时，地基土及挡土墙的自重应力固结沉降和变形已完成，通过激活填土计算单元的方法来模拟填土的填筑。

图 3　倒Y型挡土墙的有限元网格划分

大量研究表明，采用强度折减有限元方法分析挡土墙的稳定性是可行的[11-12]。本研究采用强度折减有限元方法[13-15]来计算挡土墙的抗滑稳定性。其操作步骤为：在弹塑性有限元数值计算中，首先假定强度折减系数Ftrial，然后将各土层的实际强度参数c、φ按照下式同时进行折减：

(1)

式中：cr、φr分别为折减后的黏聚力和内摩擦角。

以此对边坡进行弹塑性有限元计算，如果根据一定的失稳判据[16]确定边坡达到极限平衡状态，则与此相对应的强度折减系数Ftrial就是总体安全系数Fs，否则重新假定折减系数，重复进行计算，直至土体达到临界极限平衡状态。

2结果与分析

2.1墙趾板长度对倒Y型挡土墙稳定性的影响

基于强度折减有限元法，计算得到了墙趾板长度L1变化情况下的挡土墙后土体滑裂面的分布情况，结果见图4，相应的安全系数变化情况见图5。

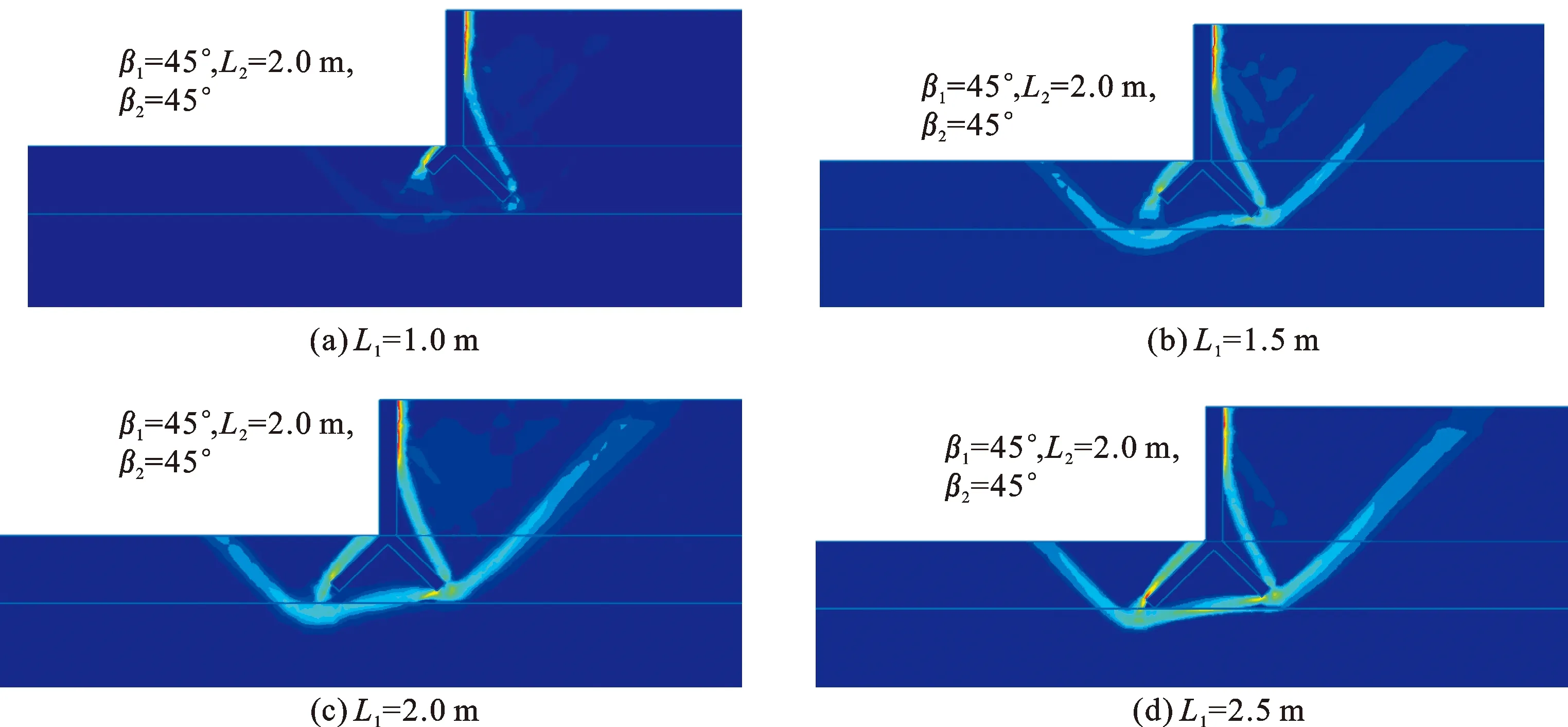
图 4　墙趾板长度(L1)对倒Y型挡土墙墙后土体滑裂面位置的影响

图 5　墙趾板长度(L1)对倒Y型挡土墙稳定性的影响

由图4-(a)可见，当墙趾板长度较小时，挡土墙呈现出倾覆破坏，滑裂面紧贴墙背，而墙后土体中无明显破裂面。由图4-(b)～图4-(d)可见，随着墙趾板长度的增大，挡土墙由倾覆破坏转变为滑移破坏，墙后土体中出现了明显的破裂面，即土体内部被剪切破坏。图5显示，墙趾板L1=1.0m时挡土墙的安全系数Fs=1.416，墙趾板L1=2.5 m时挡土墙的安全系数Fs=1.563，可见挡土墙的安全系数随着墙趾板长度的增加而增大，平均意义上讲墙趾板长度每增加0.5 m，挡土墙的安全系数提高3.5%。

2.2墙趾板与铅垂线夹角对倒Y型挡土墙稳定性的影响

墙趾板与铅垂线夹角β1变化情况下挡土墙后土体的滑裂面位置分布情况见图6，相应的安全系数的变化情况见图7。由图6可见，当β1较小时，挡土墙呈现出倾覆破坏，墙后土体中无明显的破裂面；随着β1的增大，墙后土体中出现了明显的破裂面，挡土墙由倾覆破坏转变为滑移破坏。图7表明，β1为30°时挡土墙的安全系数Fs=1.447，β1为90°时挡土墙安全系数Fs=1.684，可见挡土墙的安全系数随着β1的增加而增大，平均意义上讲β1每增加10°，挡土墙的安全系数提高2.73%。故设计中可取β1=90°，相同条件下此时的安全系数最大。

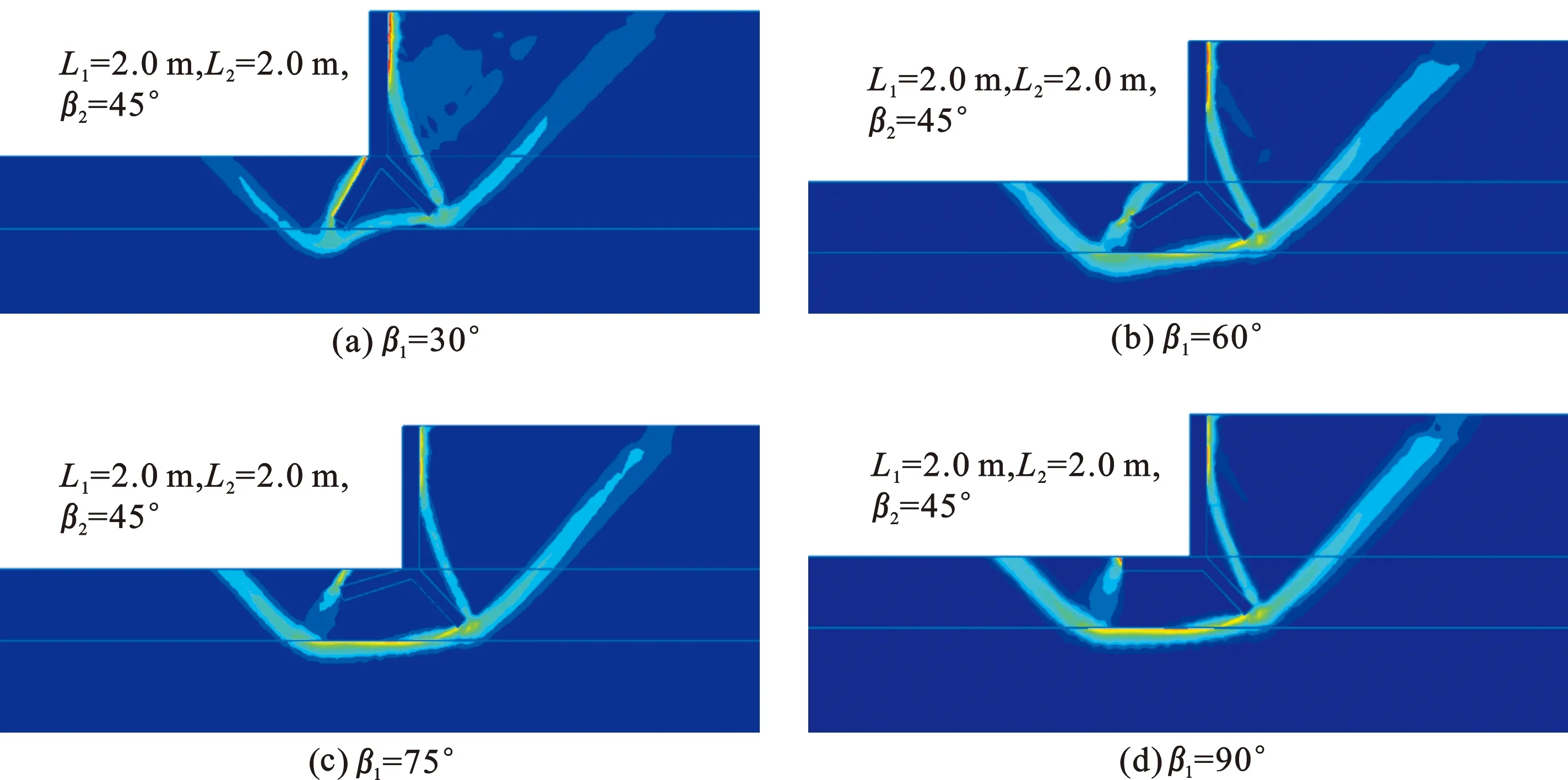
图 6　墙趾板与铅垂线夹角β1对倒Y型挡土墙墙后土体滑裂面位置的影响

图 7　墙趾板与铅垂线夹角β1对倒Y型挡土墙稳定性的影响

2.3墙踵板长度对倒Y型挡土墙稳定性的影响

图8给出了墙踵板长度变化情况下挡土墙后土体的滑裂面位置，相应的安全系数的变化情况见图9。由图8可见，随着墙踵板长度的增大，墙后土体的滑裂面向更深的土体中发展，即更多的土体被包含在滑裂范围内，滑裂面的长度也增大，滑动破坏更加困难。由图9可知，L2=1.0 m时挡土墙安全系数Fs=1.402，L2=2.5 m时挡土墙安全系数Fs=1.585，平均意义上讲墙踵板长度每增加0.5 m挡土墙的安全系数提高4.35%。因而，增加挡土墙墙踵板的长度可以增强挡土墙的稳定性。

图 8墙踵板长度L2对倒Y型挡土墙墙后土体滑裂面位置的影响

Fig.8Influence of length of the heel wall plateL2on position of fractured

surface of soil behind inverted Y type retaining wall

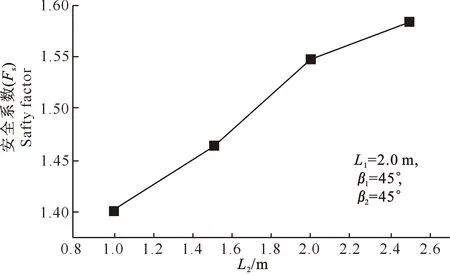
图 9　墙踵板长度L2 对倒Y型挡土墙稳定性的影响

2.4墙踵板与铅垂线夹角对倒Y型挡土墙稳定性的影响

墙踵板与铅垂线夹角β2变化情况下(β2=15°,30°,60°,75°,90°),倒Y型挡土墙墙后土体的滑裂面位置分布情况如图10所示，相应的安全系数的变化情况见图11。由图10可以看出，当墙踵板与铅垂线夹角较小时(如β2=15°)，挡土墙呈现出倾覆破坏，墙后土体中无明显的滑裂面。可见，墙踵板与铅垂线夹角必须大于一定的数值，才能使墙踵板上方的土体质量作用于墙踵板而提高挡土墙的稳定性。

图 10墙踵板与铅垂线夹角(β2)对倒Y型挡土墙墙后土体滑裂面位置的影响

Fig.10Influence of angle between the heel wall plate and the plumb lineβ2on

position of fractured surface of soil behind inverted Y type retaining wall

图11表明，挡土墙的安全系数随着墙踵板与铅垂线夹角的增大呈现出先增大后减小的趋势；当墙踵板与铅垂线夹角β2=45°时，安全系数达到最大值(Fs=1.549)，倒Y型挡土墙的稳定性最好；当墙踵板与铅垂线夹角β2>45°时，倒Y型挡土墙的稳定性逐步降低。故在设计中，墙踵板与铅垂线夹角可取β2=45°，相同条件下此时的安全系数最大。

图12给出了β2不同取值情况下挡土墙后土体的滑裂面长度变化情况。由图12可知，β2=45°时滑裂面长度最大，安全系数最大。故滑裂面长度大的挡土墙稳定性高，滑裂面长度小的挡土墙结构稳定性低。若要提高挡土墙的稳定性，本质上应使该挡土墙结构产生的滑裂面长度变大。

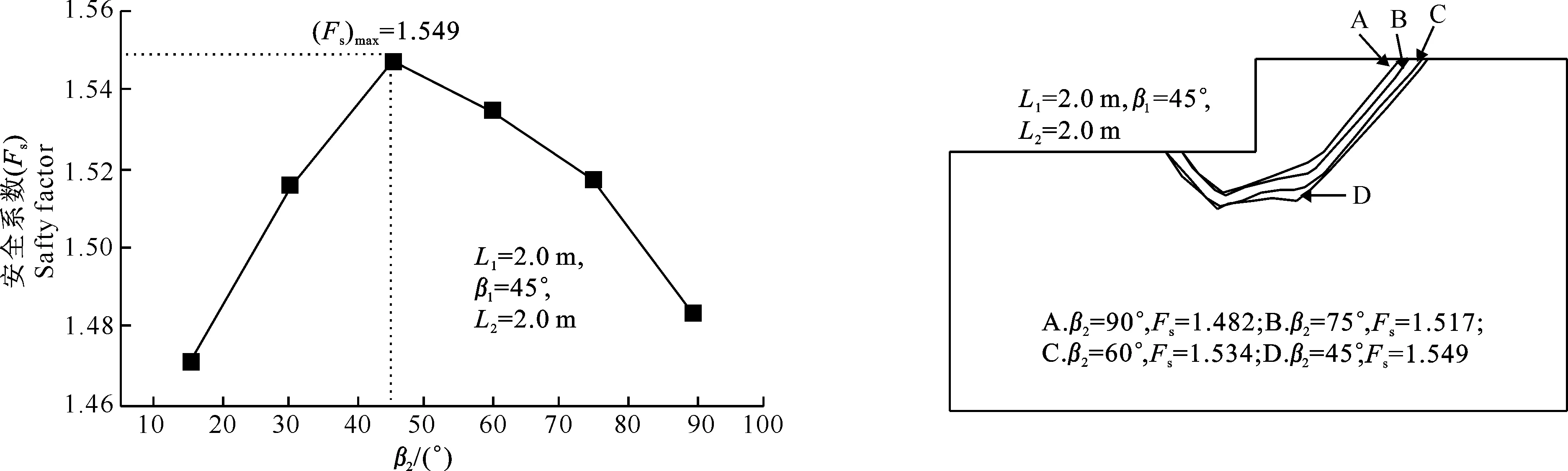
图 11　墙踵板与铅垂线夹角(β2)

3倒Y型挡土墙结构的最优构型

倒Y型挡土墙的主要设计参数包括：墙趾板的长度L1、墙趾板与铅垂线的夹角β1、墙踵板的长度L2、墙踵板与铅垂线的夹角β2。对比上述有限元计算结果可知，墙趾板与铅垂线夹角β1=90°、墙踵板与铅垂线夹角β2=45°情况下挡土墙的安全系数最高。由此可确定倒Y型挡土墙结构的最优构型如图13所示。虽然其合理性与有效性有待通过模型试验进行验证，但进一步分析图13可知其与传统的悬臂式挡土墙(图14)具有一定的相似性。两者的区别在于：传统悬臂式挡土墙的墙踵板为水平分布，而倒Y型挡土墙最优设计构型的墙踵板与铅垂线呈45°夹角。某种程度上说，传统悬臂式挡土墙可看作是本文所提倒Y型挡土墙在β1=β2=90°情况下的特例。

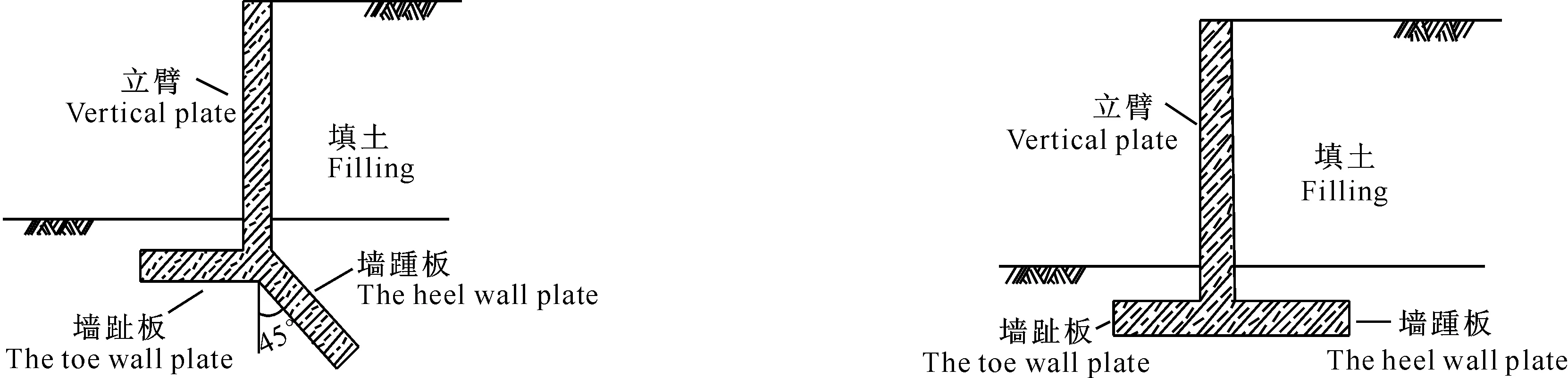
图 13　倒Y型挡土墙的最合理布置方式

对比图13与图14便产生疑问：通过旋转传统悬臂式挡土墙结构的墙踵板45°是否可提高挡土墙的稳定性？图15给出了图13与图14 2种情况下土体位移增量的分布结果。由图15可见传统悬臂式挡土墙修建于地基土Ⅰ上，其潜在破裂的土体为墙后填土，破裂面沿挡土墙底部即地基土Ⅰ顶部穿过；而对于倒Y型挡土墙的最优构型，由于其墙踵板向地基土Ⅰ倾斜插入45°，使得挡土墙破坏时的滑裂面必然经过地基土Ⅰ土体内，即填土与地基土Ⅰ共同形成潜在的破裂土体，地基土Ⅰ的参与必然可提高挡土墙的稳定性。计算得到图15(a) 的安全系数Fs=1.585，而图15(b)的安全系数Fs=1.684。

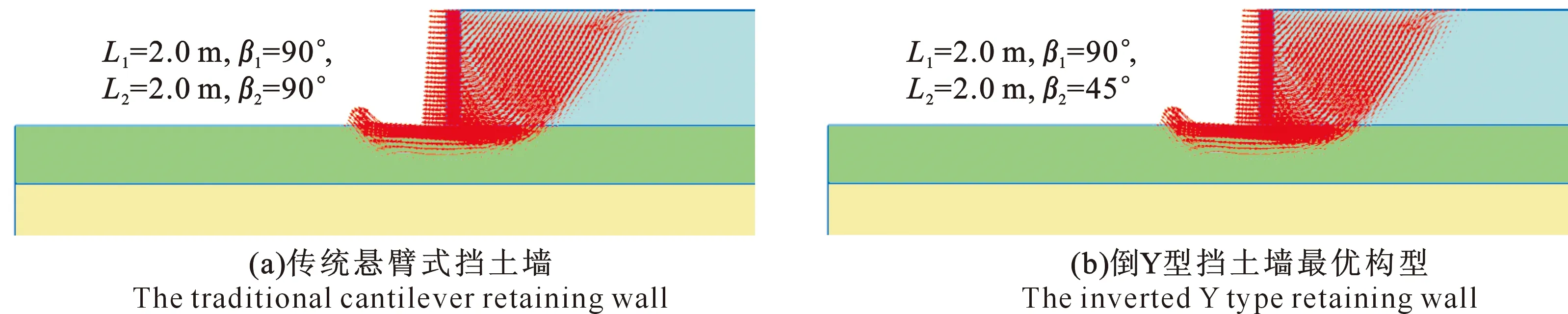
图 15　不同挡土墙结构的填土位移增量分布图

图16给出了图13与图14 2种情况下墙后土体滑裂面的分布情况，可见相同条件下倒Y型挡土墙最优构型的滑裂面长度大于传统悬臂式挡土墙，而滑裂面长度越大稳定性越高。

图 16　不同挡土墙结构的滑裂面长度对比分析

与传统的重力式挡土墙相比，倒Y型挡土墙结构具有下列特点[9]：

(1) 由挡土墙背土压力、挡土墙自重、墙踵板上的土体重力形成的合力几乎垂直作用于墙踵板的基础底面上，使得挡土墙的稳定性得到提高。即墙踵板上的土体重力有助于提高挡土墙的稳定性。而重力式挡土墙主要依靠墙身的重力来平衡土压力，工程量大，经济效果差。

(2) 倒Y型挡土墙可用于受周围条件限制或施工及开挖困难的地基，也可用于软弱地基或者承载能力较小的地基。

(3) 倒Y型挡土墙墙身可建成直立墙，墙身断面较小，圬工数量较少，体积比较轻盈，占地面积较小。

4结论

1) 随着墙趾板长度的增大，倒Y型挡土墙由倾覆破坏转变为滑移破坏，墙后土体中出现了明显的破裂面。挡土墙的安全系数随着墙趾板长度的增加而增大。

2) 倒Y型挡土墙的安全系数随着墙趾板与铅垂线夹角的增加而增大，故设计中墙趾板与铅垂线夹角可取90°。

3) 随着墙踵板长度的增大，墙后土体中的滑裂面向更深的土体中发展，即更多的土体被包含在滑裂范围内，滑裂面的长度变大，因而挡土墙的安全系数增大。

4) 倒Y型挡土墙的安全系数随着墙踵板与铅垂线夹角的增大呈现出先增大后减小的趋势。当墙踵板与铅垂线夹角为45°时，倒Y型挡土墙的稳定性最好。

5) 倒Y型挡土墙结构的最合理构型为：墙趾板与铅垂线夹角为90°、墙踵板与铅垂线夹角为45°，此时挡土墙稳定性最高。传统悬臂式挡土墙也可视为倒Y型挡土墙的一个特例。

[参考文献]

[1]梁波,王家东,葛建军,等.青藏铁路L型挡土墙的土压力实测与分析 [J].岩土工程学报,2004,26(5):627-631.

Liang B,Wang J D，Ge J J,et al.Testing and analysis of earth pressure about L type retaining wall in Qinghai-Tibet Railway [J].Chinese Journal of Geotechnical Engineering,2004,26(5):627-631.(in Chinese)

[2]胡荣华,齐明柱,余海忠,等.卸荷板挡墙的设计实践 [J].铁道建筑,2010(11):87-90.

Hu R H,Qi M Z,Yu H Z,et al.Practical design of retaining wall with relieving plate [J].Railway Engineering,2010(11):87-90.(in Chinese)

[3]阮长青,屠毓敏,俞亚南.齿坎式挡土结构物极限抗滑力研究 [J].岩土力学,2010,31(8):2514-2518.

Ruan C Q,Tu Y M,Yu Y N.Study of limit sliding resistance force on retaining structure with tenon [J].Rock and Soil Mechanics,2010,31(8):2514-2518.(in Chinese)

[4]邓国华,邵生俊,程新星.膨胀土加筋挡土墙现场试验研究与分析 [J].西北农林科技大学学报：自然科学版,2007,35(2):220-224.

Deng G H,Shao S J,Cheng X X. Field study and analysis of reinforced earth wall for expansive soils [J].Journal of Northwest A&F University：Natural Science Edition,2007,35(2):220-224.(in Chinese)

[5]铁道第二勘察设计院.铁路路基支挡结构设计规范(TB10025-2006) [S].北京:中国铁道出版社,2006.

The Second Reconnaissance and Design Research Institute of Railroad.Code for design on retaining structures of railway subgrade(TB10025-2006) [S].Beijing：China Railway Press,2006.(in Chinese)

[6]刘金龙,陈陆望,王吉利.软弱地基上齿坎式挡土结构物抗滑特征分析 [J].西北农林科技大学学报：自然科学版,2012,40(6):224-229.

Liu J L,Chen L W,Wang J L.Character of retaining structure with tenon on weak foundation [J].Journal of Northwest A&F University:Natural Science Edition,2012,40(6):224-229.(in Chinese)

[7]李海光.新型支挡结构设计与工程实例 [M].北京:人民交通出版社,2004:5-48.

Li H G.Design of new structure of retaining wall and its application [M].Beijing:China Communications Press,2004:5-48.(in Chinese)

[8]刘桂生.两种新型挡土墙 [J].中外公路,1990,10(6):20-22.

Liu G S.Two new types of retaining wall [J].Journal of China & Foreign Highway,1990,10(6):20-22.(in Chinese)

[9]陈亮,谌晓静.倒Y型挡土墙力学特性研究 [J].重庆交通大学学报:自然科学版,2013,32(3):419-423.

Chen L,Chen X J.Research on the mechanical properties of inverted Y type retaining wall [J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(3):419-423.(in Chinese)

[10]冯忠居,任文峰,谢富贵,等.公路路基特长箱涵顶进模拟试验 [J].交通运输工程学报,2007,7(4):74-78.

Feng Z J,Ren W F,Xie F G,et al.Simulation experiment about oversize box culvert jacked into highway subgrade [J].Journal of Traffic and Transport Engineering,2007,7(4):74-78.(in Chinese)

[11]梁学文,刘倩.悬臂式挡土墙的有限元分析 [J].华中科技大学学报,2003,20(2):99-102.

Liang X W,Liu Q.Finite element analysis of the cantilever retain wall [J].Journal of Huazhong University of Science and Technology,2003,20(2):99-102.(in Chinese)

[12]戴自航,林智勇,郑也平,等.L型挡土墙主动土压力计算的基底摩擦系数折减有限元法 [J].岩土工程学报,2009,31(4):508-514.

Dai Z H,Lin Z Y,Zheng Y P,et al.Finite element method for computations of active earth pressures acting on L-shaped retaining walls with reduced friction coefficients of base bottoms [J].Chinese Journal of Geotechnical Engineering,2009,31(4):508-514.(in Chinese)

[13]Dawson E M,Roth W H,Drescher A.Slope stability analysis by strength reduction [J].Geotechnique,1999,49(6):835-840.

[14]Manzari M T,Nour M A.Significance of soil dilatancy in slope stability analysis [J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2000,126(1):75-80.

[15]万少石,年廷凯,蒋景彩,等.边坡稳定强度折减有限元分析中的若干问题讨论 [J].岩土力学,2010,31(7):2283-2288.

Wan S S,Nian T K,Jiang J C,et al.Discussion on several issues in slope stability analysis based on shear strength reduction finite element methods (SSR-FEM) [J].Rock and Soil Mechanics,2010,31(7):2283-2288.(in Chinese)

[16]刘金龙,栾茂田,赵少飞,等.关于强度折减有限元方法中边坡失稳判据的讨论 [J].岩土力学,2005,26(8):1345-1348.

Liu J L,Luan M T,Zhao S F,et al.Discussion on criteria for evaluating stability of slope in elastioplastic FEM based on shear strength reduction technique [J].Rock and Soil Mechanics,2005,26(8):1345-1348.(in Chinese)

Stability of inverted Y type retaining wall against sliding

SHI Xiao-ping

(SchoolofResourceandEnvironmentalEngineering,HefeiUniversityofTechnology,Hefei,Anhui230009,China)

Abstract:【Objective】 The stability of inverted Y type retaining wall was studied to provide reference for the design of inverted Y type retaining wall in areas with small filling range,limited construction space,and having difficulty in foundation excavation.【Method】 Based on shear strength reduction finite element method,the stability of inverted Y type retaining wall with different parameters was analyzed to determine the optimal design value.【Result】 The stability of inverted Y type retaining wall on average increased by 3.5% when the length of the toe wall plate increased by 0.5 m,the stability increased by 2.73% when the angle between the toe wall plate and the plumb line increased 10°,and the stability increased by 4.35% when the length of the heel wall plate increased 0.5 m.While the stability of inverted Y type retaining wall increased first and decreased later with the increase of the angle between the heel wall plate and the plumb line.【Conclusion】 When the angle between the toe wall plate and the plumb line valued 90° and the angle between the heel wall plate and the plumb line valued 45°,the stability of retaining wall obtained its maximal value.The stability of retaining wall enhanced when the length of the toe wall plate or the length of the heel wall plate increased,but the specific length of the toe wall plate or the heel wall plate should be calculated and determined according to the geological conditions and stability requirement.The traditional cantilever retaining wall could be treated as a special case of inverted Y type retaining wall.

Key words:inverted Y type retaining wall;anti-slide stability;slip surface;the toe wall plate;the heel wall plate

DOI：网络出版时间:2016-02-0209:3710.13207/j.cnki.jnwafu.2016.03.028

[收稿日期]2014-07-16

[基金项目]国家自然科学基金项目(41306088);安徽省自然科学基金项目(1308085ME61)

[作者简介]施小平(1971-),男,安徽枞阳人,讲师,博士,主要从事岩土工程研究。E-mail:165638797@qq.com

[中图分类号]TU432

[文献标志码]A

[文章编号]1671-9387(2016)03-0203-08