LIDAR点云数据全自动滤波算法研究

李　健, 方宏远, 崔雅博, 范　涛

LIDAR点云数据全自动滤波算法研究

李健1, 方宏远1, 崔雅博2, 范涛3

(1.郑州大学 水利与环境学院，河南 郑州 450001；2.开封大学 实验实训中心，河南 开封 475004；

3.河南省地质环境监测院，河南 郑州 450001)

摘要：提出了一种基于移动最小二乘法的点云数据全自动滤波算法，该方法首先对LIDAR点云数据进行合理分块，并建立分块网格的动态四叉树空间索引，便于数据操作和管理.对分块网格中的点云数据利用精简移动最小二乘法拟合出参考地形，将拟合得到的参考地形用于LIDAR点云高程阈值的迭代计算，将每次迭代前后高差小于阈值的点划为地面点，其余点划分为非地面点，迭代运算直至阈值满足要求为止.实验表明，精简移动二乘法效率高，计算量小，并且精度高，适合点云数据DEM(digital elevation model)拟合，利用该算法对LIDAR点云数据进行滤波的速度快、精度高，能够有效地识别地面点和非地面点，并保留地形的细节信息.

关键词：点云数据；数字地面模型；滤波算法；动态四叉树；移动最小二乘法

0引言

随着激光技术的快速发展和完善，激光数据在众多领域得到了广泛的应用.由于激光能在短时间内获得地物三维坐标信息，并且数据量极大，故而如何快速从海量LIDAR点云数据中提取有用的信息是目前研究的热点和难点[1].国内外许多学者都对点云滤波进行了讨论和研究，并且提出了许多滤波算法，包括基于数学形态学的滤波算法[2-3]、基于坡度的滤波算法[4-6]、基于TIN的渐进加密算法[7-8]等，都取得了一些研究成果，但其中还存在一些问题尚未解决.不管是机载LIDAR数据还是地面LIDAR数据大部分是基于激光点云中高程突变信息进行滤波，假定点云中高程低的点为地面点，高程较高的点为非地面点，由于系统误差的存在，这种情况未必完全正确.另外一些滤波算法适用范围有限.从上述问题可看出，提出一种简单、快速、适用范围广、效率高的点云滤波算法是非常必要的[9].

由于激光点数据量大，并且点云数据的不规则、散乱复杂等性质决定了点云数据处理工作的复杂困难[10-11].针对LIDAR点云数据的特点，笔者提出了先将点云数据进行网格分块，保证点云数据的原始性，减少单次数据处理量.对分块数据建立空间索引，提高点云数据处理的效率.

1关键技术与算法

1.1LIDAR点云数据的滤波流程

将海量激光点云分块并建立相应的空间索引关系后，进行地物的自动过滤处理，滤波要考虑当前点所在的网格，并对其进行计算，每次计算的结果再以索引的方式动态存储，作为下次迭代计算的基础数据，具体滤波流程如图1所示.

1.2点云数据的网格分块与动态四叉树空间索引

为了进行激光点云的海量数据管理、处理与显示，对激光点云分块处理显得尤为必要.分块的大小直接影响到数据处理层次及深度，相应地影响算法的效率.分块越小，分割越细，效率就越低，其合并的区域相对增大，数据的压缩比就越高；反之，效率就越高，而压缩比相对降低.最小格网大小的选择应是最小采样间距的整数倍，具体数值的确定取决于被测对象的复杂度、仪器的最小采样间距以及期望的数据压缩比.

图1　点云滤波处理流程图

为了高效地管理和存储分块网格及网格内的激光点云数据，需要对所有存在点的网格与点云之间建立索引关系，在对点云进行处理和过滤时，只需要考虑点所在的网格即可，这里采用四叉树结构[12].

由于激光点云的分布不均匀和边界形状极其不规则，为了克服常规四叉树空间索引结构中的问题，笔者采用空间动态四叉树的方法对分块网格建立索引关系.其算法要点为：在开始建立四叉树时，不需要事先确定工作区域的范围，只须把要插入空间数据库的第一个对象的MBR(minimum bounding rectangle)中心作为四叉树的顶点，随着数据处理工作的进行，对作业空间进行分解.

1.3精简移动最小二乘法拟合DEM

移动最小二乘法提供一种较高次数的多项式逼近方式对散乱点云进行曲面拟合[13]，并且要求拟合函数在各个节点处的误差的平方和最小，能够保证比较高的精度.用该算法拟合的曲面比较平滑，与实际曲面近似[14-15].但是移动最小二乘算法比较复杂，运算效率不高，如果点云数据量比较大，则处理比较困难，因此需要对该方法进行精简，在保证精度前提下提高其运算效率.精简移动最小二乘法采用带权的正交函数作为基函数[16-18]，在求解系数矩阵时可只考虑对角线元素，不用求逆矩阵，减少了运算量、提高了运算效率，同时也提高了精度，适合于数据量比较大的点云数据拟合.

最小二乘拟合函数：

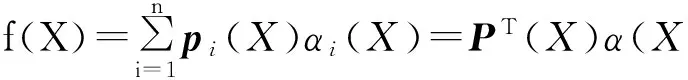
(1)

式中：αi(X)为待求系数(i=1,2,...，n)，是坐标X的函数；pi(X)称为基函数，它是一个k阶完备的多项式；n是基函数的项数.

对于二维空间拟合，基函数PT(X)的形式为

线性基：PT=(1,x1,x2).

(2)

(3)

为了使得曲面在点x局部拟合最优，定义误差方程：

(4)

式中：w(X-Xi)为权重函数;m为计算域内节点总数.

式 (4) 可写为

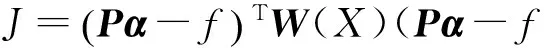
(5)

式中：

(6)

(7)

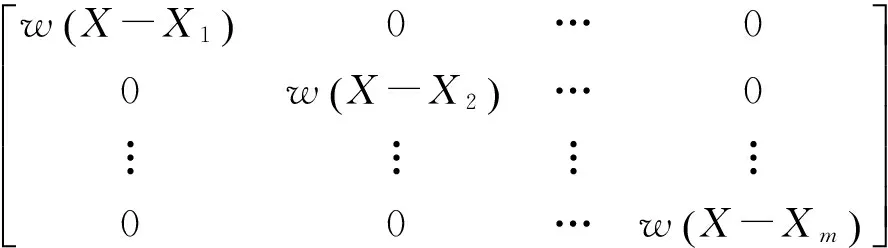
(8)

待求系数α(x)通过求取目前函数J的极值获取(见式(9)).

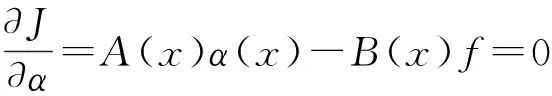
(9)

式中：

A(x)=PTW(x)P.

(10)

B(x)=PTW(x).

(11)

为了避免式(9)在求解过程中出现病态和奇异，这时如果假定对于点集{x}和权{wiJB(i=1,2,...n)},若存在一组函数pi(x)(i=1,2,...,n)满足：

(12)

则称pi(x)(i=1,2,…n)为点集{x}和权{wi}的正交函数集，那么移动最小二乘可变为：

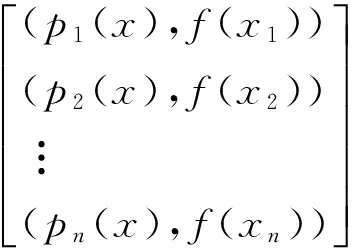
(13)

那么很容易就解出αi(x)：

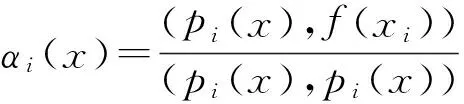
(14)

待定系数αi(x)可以通过求解式(14)得到，并且αi(x)的求解过程避免了求矩阵的逆，避免了求解病态方程，计算效率得到了提高.

为了验证该算法，利用扫描点云数据中2 658个点来检测对比精简移动最小二乘算法与移动最小二乘算法拟合的DEM，图2为在MATLAB中使用移动最小二乘拟合的DEM，耗时156s，从拟合DEM数据可以看出构建的DEM精度较低，而使用IDL(interactivedatalanguage)编程开发的精简移动最小二乘法拟合的DEM(如图3所示)，只用了30s，时间减少了126s，效率得到提高，从效果来看,拟合DEM比较平滑，与实际地形较接近.

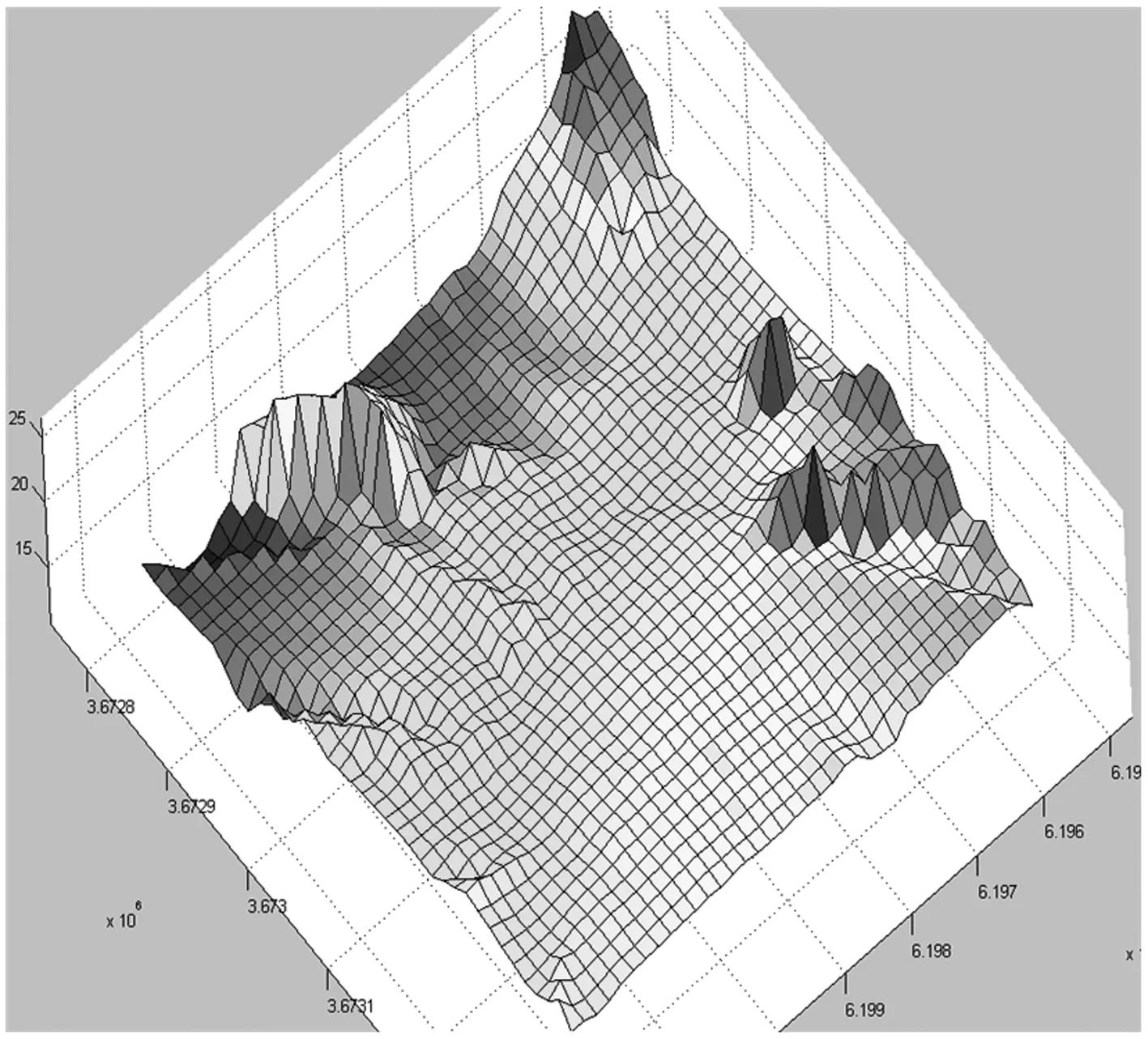
图2　MLS算法拟合DEM

2实验与应用

笔者主要通过IDL编程实现上述算法， IDL是面向矩阵、语法简单的第四代可视化语言，可以应用于任何领域的三维数据可视化、数值计算、三维图形建模、科学数据读取等功能中.IDL是完全面向矩阵的，它具有快速分析超大规模数据的能力，这在海量点云处理方面具有独特的优势[19].

图3　精简MLS算法拟合DEM

为了验证本算法的精度，将滤波算法得到的地面点云数据进行抽稀，与本区域内采集GPS测量数据进行对比，来评定该算法的精度.通过十站扫描采集约一平方公里的点云，原始点云数据约2.5G(如图4)，获得本区域内200个GPS点数据.将扫描点云数据拼接后使用笔者提出的算法对点云数据进行滤波，得到地面点云数据并进行抽稀，如图5所示.将抽稀后的地面点云数据在CAD中进行高程展点，并将200个GPS点高程数据加入CAD中，将两组数据进行统计对比，如图6所示.浅色为激光点云高程数据，深色为GPS高程数据.在这里由于获得的地面点云数据与采集的GPS点坐标不是同名点，因此只能根据离GPS点最近或者附近的地面激光点的高程进行统计，存在一些高程异常点，高程点误差范围见表1.

图4　原始扫描激光点云数据

利用笔者提出的滤波算法对十站扫描点云数据滤波，过滤后地面激光点云个数约为8 145 631个.在滤波算法中分块网格大小为2 m，迭代3次，普通笔记本电脑过滤时间约1 min将过滤后激光点云数据构建间距2 m的DEM网格如图7所示.

图5　滤波抽稀10 m点云数据

图6　激光点云高程与GPS高程数据对比

绝对值高程误差/cm激光点云数目<1542～5776～102811～152216～2014高程异常点7

图7　过滤后的激光点云数据生成DEM数据

3结论

(1)根据LIDAR点云数据的特点，提出了基于网格分块的过滤方法，并建立了分块网格的动态四叉树的空间索引方法，解决了海量激光点云数据的存储和管理，进而实现了海量激光点云数据的快速处理.并且使用动态最小二乘法拟合DEM对点云数据进行滤波，拟合平面比较平滑，与实际地形接近.

(2)从分类得到点云数据与GPS高程点精度对比可以看出，笔者所采用的滤波算法精度较高，能够快速有效地从激光点云数据中识别地面点和非地面点，实用性强.

(3)从文中两个案例可以看出本算法适用于机载LIDAR和地面LIDAR的滤波处理，且能够高效地对海量点云数据进行滤波处理.但对一些特殊地形(如悬崖)仍然存在一定的问题，需要采用转换坐标系或进行局部过滤等处理方法.

参考文献：

[1]AXELSSON P. Processing of laser scanner data algorithms and applications [J]. ISPRS international journal of photogrammetry and remote sensing, 1999,54(2/3):138-147.

[2]隋立春,张熠斌.基于改进的数学形态学算法的LiDAR点云数据滤波[J].测绘学报,2010, 39(4): 390-396.

[3]罗伊萍,姜挺,龚志辉,等. 基于多尺度和自适应数学形态学的数据滤波方法[J].测绘科学技术学报,2009, 26(6):426-429.

[4]杨应,苏国中,周梅.影像分类信息支持的LiDAR点云数据滤波方法研究[J].武汉大学学报(信息科学版),2010, 35(12): 1453-1456.

[5]袁枫,张继贤,张力,等.结合强度信息的LiDAR数据滤波方法[J].测绘科学,2010,35(5): 39-41.

[6]刘凯斯.机载激光LiDAR点云数据滤波和分类算法研究[D].北京：首都师范大学资源环境与旅游学院,2014.

[7]左志权,张祖勋,张剑清.知识引导下的城区LiDAR点云高精度三角网渐进滤波方法[J].测绘学报,2012, 41(2): 246-251.

[8]AXELSSON P. DEM Generation from laser scanner data using adaptive TIN models [J]. International archives of photogrammetry and remote sensing, 2000,XXXIII (B4):110-117.

[9]KRAUS K, PFEIFER N. Determination of terrain models in wooded areas with airborne laser scanner data [J]. ISPRS Journal of photogrammetry and remote sensing, 1998, 5(4):193-203.

[10]李乐林. 基于等高线族的机载LiDAR数据建筑物三维模型重建方法研究[D].武汉:武汉大学测绘遥感信息工程国家重点实验室,2012.

[11]KHAMARRUL A R, MICHELE S C J， VAN W., et al. Generating an optimal DTM from airborne laser scanning data for landslide mapping in a tropical forest environment [J]. Geomorphology,2013,190:112-125.

[12]赵波,边馥苓. 面向移动GIS的动态四叉树空间索引算法[J].计算机工程,2007,33(15):86-88.

[13]LANCASTER P. SALKAUSKAS K. Surfaces generated by moving least squares methods [J]. Mathematics of computation,1981,37:141-158.

[14]TSCHKO T B, Lu Y Y, GU L. Elements-free galerkin methods [J]. International journal for numerical methods in engineering,1994,37:229-256.

[15]LEVIN D. The Approximation power of moving least squares [J]. Mathematics of computation,1998, 67:1517～1531.

[16]陈美娟,程玉民.改进的移动最小二乘法[J].力学季刊,2003,24(2):266-272.

[17]倪慧,李重,宋红星,等.带插值条件的最小移动二乘曲线拟合[J].浙江理工大学学报,2011,28(1):135-139.

[18]任红萍, 程玉民,张武.改进的移动最小二乘插值法研究[J].工程数学学报,2010,27(6):1021-1029.

[19]韩培友. IDL可视化分析与应用[M].西安:西北工业大学出版社,2006.

An Automatic Point Clouds Filtering Algorithm Based on Grid Partition and Simplified Moving Least Squares

LI Jian1, FANG Hongyuan1, CUI Yabo2, FAN Tao3

(1 College of Water Conservancy & Environmental Engineering, Zhengzhou University, Zhengzhou 450001， China; 2 Training Center，Kaifeng University, Kaifeng 475004， China; 3 Henan Geological Environment Information, Zhengzhou 450001， China)

Abstract:An automatic point clouds filtering algorithm is presented on the basis of Grid Partition using Dynamic Quad Trees and reference surface fitted by Moving Least Squares. The filtering processing contains three major steps: Firstly, it gives the LIDAR point clouds reasonable grid partitions and establishes the corresponding dynamic quad trees spatial indices. Secondly, the points in the partitioned grids are utilized to fit a DEM reference plane using moving least squares technology. Finally, the elevation threshold is setup to separate ground points from those non-ground ones who are positioned above the reference plane and have a distance exceeding the threshold value to the plane. The aforementioned steps have to be repeated on the obtained ground points with gradually decreasing thresholds and grid size until desired precision is achieved. The experiments show that simplified moving least squares is high efficiency, small amount of calculation and high precision DEM data for point cloud fitting, and the filtering algorithm has high precision and can effectively identify ground points and non-ground ones without losing the detailed information of topography.

Key words:point clouds data; DEM; filtering algorithm; dynamic quad trees; moving least square

收稿日期:2015-04-02；

修订日期：2015-10-28

基金项目：国家自然科学基金青年基金资助项目(41404096)；河南省教育厅基金资助项目(14A420002,15A420002)

作者简介：李健(1983—)，男，河南孟州人，郑州大学讲师，博士，主要从事点云数据处理，E-mail:jianli@zzu.edu.cn.

文章编号:1671-6833(2016)01-0092-05

中图分类号：P237

文献标志码：A

doi:10.3969/j.issn.1671-6833.201504004

引用本文：李健, 方宏远, 崔雅博，等.LIDAR点云数据全自动滤波算法研究[J].郑州大学学报(工学版)，2016,37(1):92-96.