多指标约束下齿轮传动机构模糊可靠性优化设计

胡启国，谢国宾，罗天洪,庹　奎

多指标约束下齿轮传动机构模糊可靠性优化设计

胡启国，谢国宾，罗天洪,庹奎

(重庆交通大学 机电与汽车工程学院，重庆 400074)

摘要：针对齿轮传动的优化设计问题，以模糊数学为基础，运用可靠性优化设计理论，将膜厚比、临界转速比纳入约束条件，考虑齿轮应力及强度的概率分布，建立了泥浆泵齿轮传动机构的模糊可靠性优化设计数学模型，并通过运用Matlab遗传算法工具箱编程求解，得出全局最优解.结果显示，齿轮传动的综合性能得到有效改善，并证明了优化方法的正确性与合理性，为齿轮传动优化设计提供了新的参考.

关键词：齿轮传动；多指标约束；模糊可靠性；优化设计

0引言

随着齿轮传动机构的广泛应用，齿轮的润滑问题也日益引起人们的关注. 美国齿轮制造者协会(AGMA)曾建议把弹流油膜厚度计算作为齿轮设计的一个重要部分[1]. 也正因如此，润滑膜厚度被认为是齿轮传动设计评价的指标之一[2]，所以，为提高齿轮传动的抗胶合能力和润滑性能，将膜厚比作为约束条件是有必要的.

基于振动理论，齿轮动力学中提出了关于临界转速比的计算公式，可以将此公式直接引入到优化设计约束条件中，这样，所建立的静态优化数学模型就隐含了一些动态性能指标[3].

在机械设计领域中出现的众多现代设计方法中，可靠性优化设计方法的发展给整个机械设计学科带来了深刻的影响，该方法的应用取得了良好的效果[4-6]. 根据国内外对齿轮的相关实验结果及对齿面强度和应力的研究分析[7-8]，笔者将圆柱齿轮应力及强度按对数正态分布计算，弧线圆锥齿轮应力及强度按正态分布计算.

笔者以泥浆泵齿轮传动机构设计为例，在静态优化设计中引入部分动态性能指标，同时考虑润滑油膜厚度的影响，针对存在的模糊因素，运用模糊可靠性优化理论，以寻求最优的设计参数为宗旨，建立单目标模糊可靠性优化设计数学模型.

1可靠性优化设计建模

1.1建立目标函数

泥浆泵齿轮传动机构的结构示意图如图1所示. 第一级传动为弧线圆锥齿轮副，两齿轮轴轴交角∑=90°；第二级传动为斜齿圆柱齿轮副；第三级传动为直齿圆柱齿轮副.

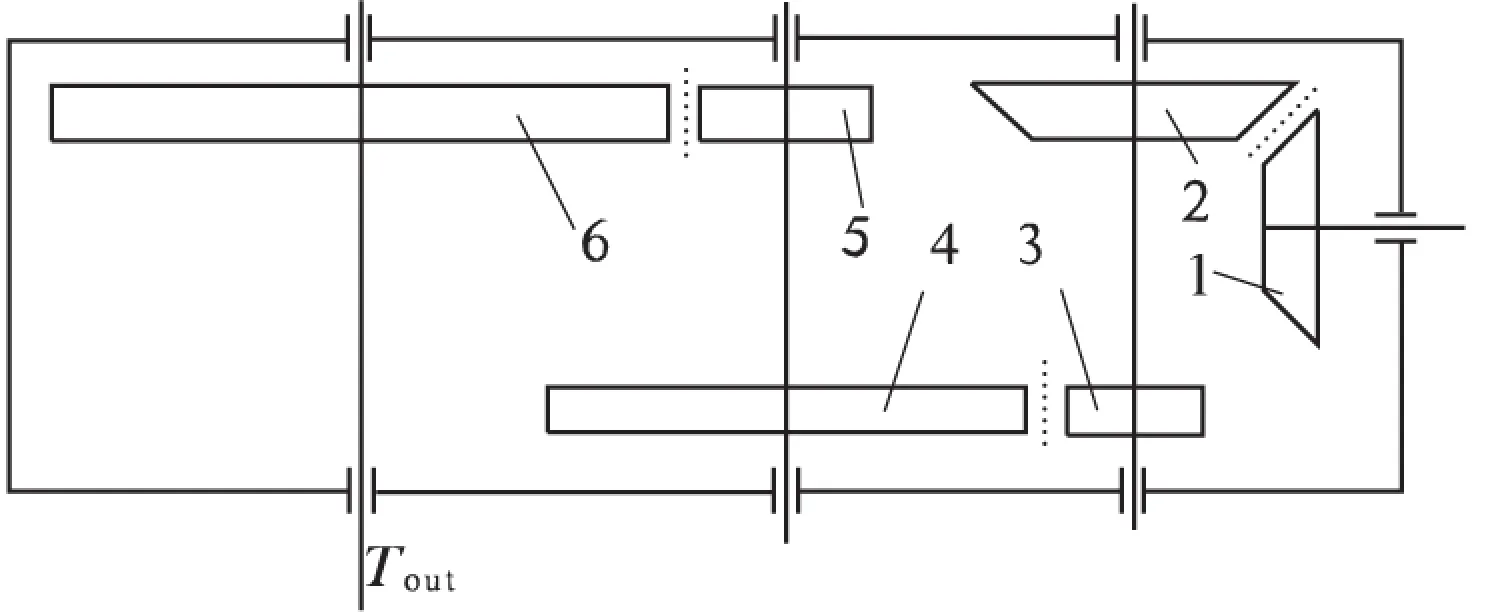
图1　泥浆泵齿轮传动系统结构简图

为使整个系统重量较轻，达到齿轮传动结构最紧凑的目的，应使齿轮传动机构的总体积最小. 笔者以6个齿轮的体积之和最小作为优化模型的目标函数.

根据圆锥齿轮副的正确啮合条件及各参数之间的计算关系，并以m1、β1、Z1、i1、φR分别代表圆锥齿轮大端模数、名义螺旋角、小锥齿轮齿数、传动比和齿宽系数，可得圆锥齿轮副的体积为

式中：δ1、δ2分别为两锥齿轮的节锥角；cos (0.5β1)是考虑到该齿轮为弧线锥齿轮而引入的，加入此项，使螺旋角β1对目标函数有所影响，能满足优化计算的需要.

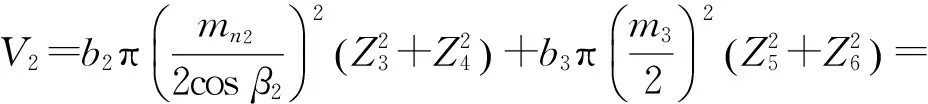
(2)

式中:φd2、φd3分别为第二、三级传动中齿轮副的齿宽系数；i2、i3分别为第二、三级传动的传动比；Z3、Z4、Z5、Z6分别为第3、4、5、6号齿轮的齿数；mn2为第二级传动中齿轮副的法面模数；m3为第三级传动中齿轮副的模数；β2为第二级传动中齿轮副的螺旋角.

由式(1)、(2)可得该齿轮传动机构的总体积，即模糊可靠性优化设计的目标函数为：

(3)

1.2确定设计变量

设计变量的选取应结合目标函数，同时必须考察这种参数是否能够控制，变量之间是否相互独立.

由式(3)可知，式中所包含的参数都能对齿轮的体积造成影响，且均为锥齿轮或圆柱齿轮的设计参数，相互独立，故取设计变量为：

1.3建立约束条件

1.3.1接触疲劳强度和弯曲疲劳强度可靠度约束

根据设计要求，接触疲劳强度和弯曲疲劳强度的可靠度需不小于0.999，即：

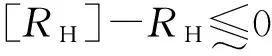
(4a)

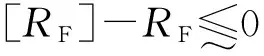
(4b)

由应力-强度正态分布的干涉模型可知，可靠度R与可靠度系数ZR有一一对应的关系，故式(4)亦可表示为：

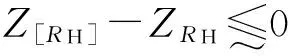
(5a)

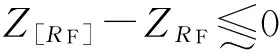
(5b)

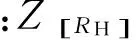
根据应力及强度分布规律，可分别得出圆锥齿轮副接触疲劳强度和弯曲疲劳强度可靠度系数：

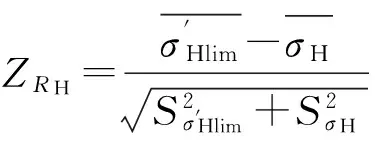
(6a)

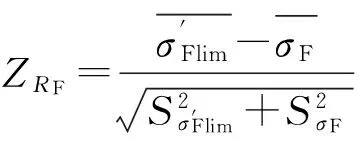
(6b)

圆柱齿轮副接触疲劳强度和弯曲疲劳强度可靠度系数：

(7a)

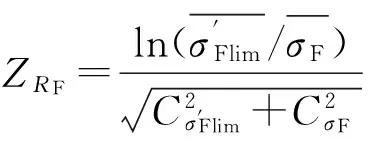
(7b)

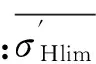
1.3.2齿轮传动节点处膜厚比约束

研究表明，基于Dowson-Higginson公式计算的油膜厚度的结果同实验测量值非常接近[1]. 根据Dowson-Higginson公式，线接触问题的最小油膜厚度hmin为hmin=2.65α0.54(ηoU)0.7R0.48E′-0.03(F/L)-0.13.

(8)

式中:α为润滑油黏压系数，m2/N；ηo为润滑油常压下的黏度，Pa·s；U为接触点处润滑油卷吸速度，m/s；E′为当量弹性模量，N/m2；R为齿轮啮合点的当量曲率半径，m；F/L为单位接触宽度上的载荷，N/m. 查阅参考文献[9]可得式(8)中参量的计算方法.

根据摩擦学知识，可以用膜厚比λ来大致估计两滑动表面所处的摩擦(润滑)状况，其大小不仅取决于最小油膜厚度，还与滑动表面的形貌轮廓有关，膜厚比公式为

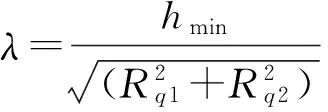
(9)

式中:Rq1、Rq2分别为两接触齿面形貌轮廓的均方根偏差，μm. 润滑理论方面的专家Akbarzadeh曾指出：当λ介于1和3之间时，两齿面处于混合摩擦(润滑)状态，齿面间磨损缓慢；当λ大于3时，两齿面处于流体摩擦(润滑)状态，为理想状态，齿面通常不会发生磨损和胶合[10]. Nogueira在分析齿轮损伤与油膜参数的关系时，发现当λ大于1.5时，齿轮处于正常工作状态(非边界润滑状态)[11]. 结合齿轮传动系统工作的实际情况，取膜厚比1.5<λ<3.0，则齿轮传动节点处膜厚比约束为

1.53.

(10)

1.3.3动态性能约束

对于大多数工业齿轮，都是工作在亚临界区. 国标中规定，当临界转速比N≤0.85时，定义为亚临界区.故得到临界转速比的约束条件为

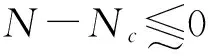
(11)

式中：Nc为允许临界转速比，Nc=0.85；N为临界转速比，N=n1/nE1，n1代表小齿轮转速，nE1表示临界转速.

1.3.4设计变量的边界约束条件

(1)齿轮模数的约束.

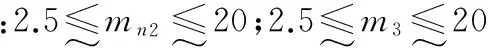
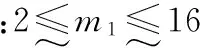
考虑到齿轮传动机构随着速度的降低，各级齿轮所受圆周力将逐级增大的特性，同时结合设计经验，应使各级模数符合递增的原则，所以有：

m1-mn2≤0，mn2-m3≤0.

(2)小齿轮齿数的约束.

(3)螺旋角的约束.

(4)传动比的约束.

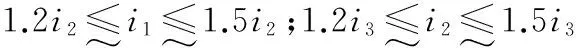
(5)齿宽系数的约束.

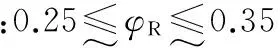
1.3.5结构约束条件

为避免齿轮5与锥齿轮2发生碰撞，取最小间隙Δ=5 mm，得到：

(12)

式中：da2为齿轮2的大端直径；da5为齿轮5的齿顶圆直径；a34为齿轮3和4的中心距.

2模糊约束条件转化为普通约束

2.1模糊约束的转换

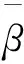
(13)

式中:λ*表示最优水平截集值，可以运用模糊综合评判法求出其值.

对设计变量的边界约束和膜厚比约束，采用线性隶属函数中的对称梯形分布；对结构约束、可靠度约束，采用升半梯形分布；对动态性能约束，采用降半梯形分布.

2.2最优水平截集值的求解

2.2.1因素集的建立

针对泥浆泵齿轮传动系统，找出对其性能的主要影响因素，按每一因素影响的不同分为5个等级如表1所示， 因素集为：

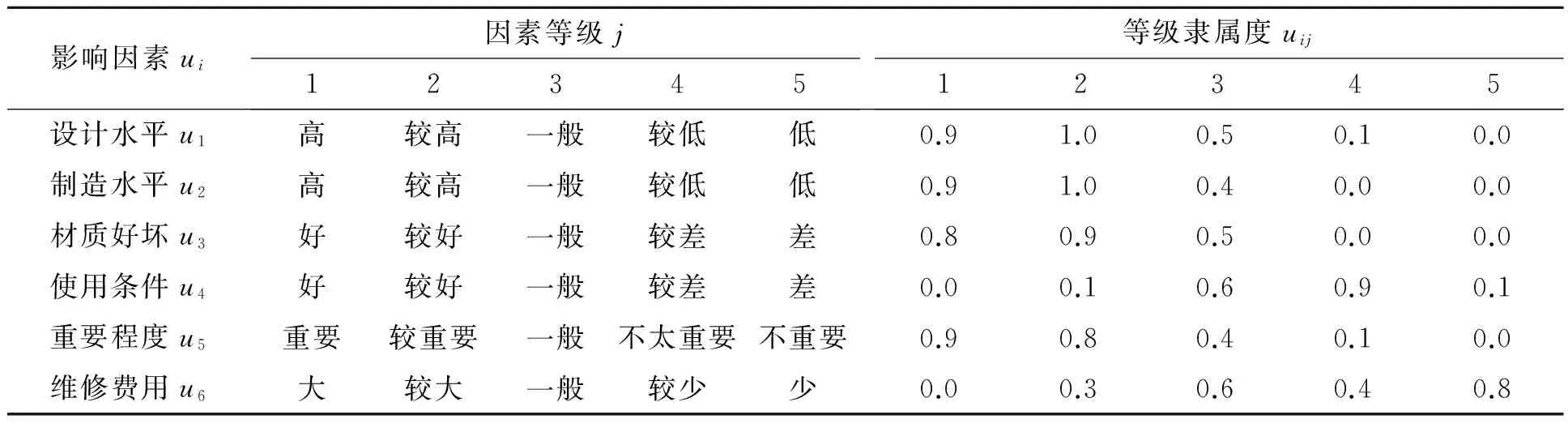
U=(u1,u2,…,u6).

2.2.2备择集的建立

把评判者对评判对象截集水平做出的各种评判结果作为一个集合，此集合由12个离散值组成，且λ∈[0，1]，其备择集为：

2.2.3权重集的建立

1)因素等级的权重集.表1中，uij表示第i个因素的第j个等级对该因素的隶属度. 将uij归一化，即可得第j个因素等级的权重aij，由此可得第i个因素等级的权重集为：

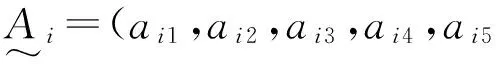
2)因素的权重集.根据各个因素对评判对象的影响，赋予各个因素相应的权重，确定因素权重集为

2.2.4建立因素等级评判矩阵

根据各个因素等级对备择集中第k(k=1, 2,…,12)个元素的隶属度，建立各因素的各个等级对备择集中各元素的单因素评价，得到等级评判矩阵.

2.2.5模糊综合评判

采用M(·,+)算子，可得一级模糊综合评判集为：

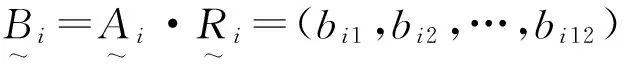
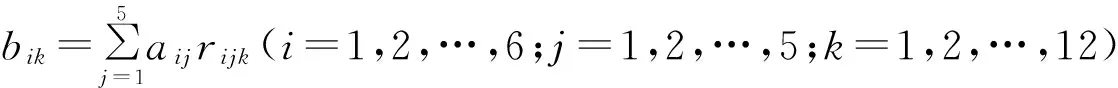
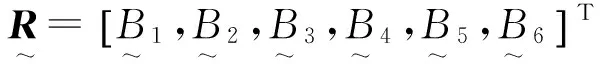
综合考虑各因素的影响，由模糊变换得二级模糊综合评判集：

2.2.6评定指标的处理

采用加权平均法，将bj看作权数，对各备择元素λj进行加权平均，所得值作为评判结果，即

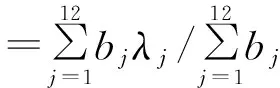
计算得最优水平截集λ*= 0.594 5. 将λ*= 0.594 5带入到在2.1中转化后的普通约束条件中，即可与式(3)组成模糊可靠性优化设计数学模型. 该模型由1个目标函数、13个自变量、24个线性不等式约束和16个非线性不等式约束组成.

3应用实例

已知泥浆泵齿轮传动机构的传递功率为P=740 kW，输入轴转速n1=1 800 r/min，总传动比i=13.85，弧线圆锥齿轮材料为20CrMnTi，渗碳淬火，齿面硬度为58～65 HRC. 圆柱齿轮大齿轮材料为45号钢，正火处理，硬度为220～260 HBW；圆柱齿轮小齿轮材料为45号钢，调质处理，硬度为230～300 HBW.

基于遗传算法良好的可操作性及较高的并行全局搜索能力，笔者选用MATLAB R2010b中的GADS遗传算法工具箱进行求解. 对齿轮的齿数、模数这些离散型变量先将其当做连续变量求解，然后把求出的解圆整或凑整到相近的离散值.

根据第2节中所建立的优化模型，编写MATALB遗传函数程序进行求解，经过50代繁殖取得最优，最优适应度值如图2所示.

图2　最优个体适应度函数值

结合实际情况，对相应的参数优化结果进行圆整，圆整后得到的结果与原设计参数的对比如表2所示.

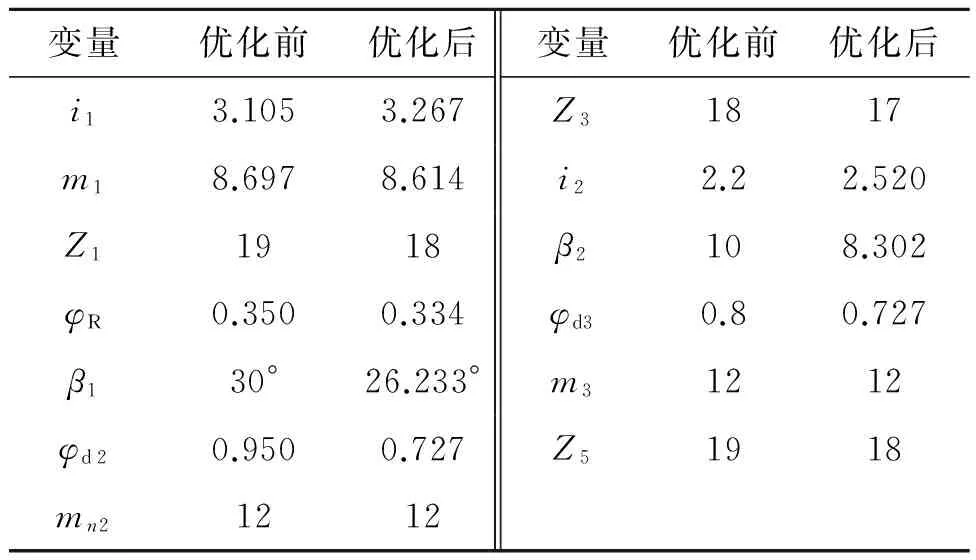
表2　设计参数的对比

经过圆整后齿轮传动机构的总体积为7.688 3×107mm3，相较原设计体积8.969 0×107mm3减少了14.27%，达到了减小体积、节省材料的目的.

根据该机构的使用期限及疲劳强度寿命系数公式，结合式(6)编程可计算出可靠度与时间的变化关系，与优化前的对比结果如表3所示.

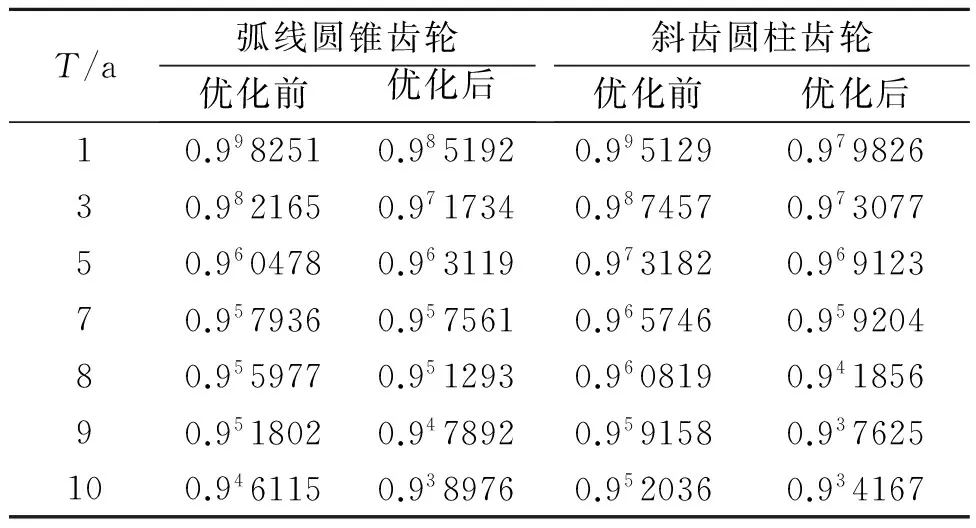
表3　接触强度可靠度的对比

注：0.99表示在小数点后有9个9.

从表3中可以看出，优化前的数据10 a后其可靠度最低的仍能达到0.946115，这很显然造成了材料的浪费. 而按笔者的设计方法所得到的齿轮传动的可靠度值相较之前虽略有降低，但在10 a的寿命期限内均能达到所要求的可靠度为0.999，仍在要求范围内，刚好满足设计使用期限，实现零部件的合理利用. 按照同样的方法可得到齿轮弯曲强度可靠度与时间的对应关系，经过验证，具有与接触强度可靠度一致的效果，在此就不赘述.

表4为优化前后膜厚比的对比，由表4可以看出，三级传动中的膜厚比具有不同程度的增加，对于弧线圆锥齿轮，位于高速级，承受扭矩较小，且其结构形式导致其承受复杂的载荷，使其润滑要求也相应较高，但在此膜厚比仅略有降低，均在要求范围内，因此不影响笔者分析结果.对于直齿圆柱齿轮，其位于低速级，且承受较大扭矩，润滑油膜较易遭到破坏，对其良好润滑极其重要，所以较高的膜厚比能够保证其有良好的润滑.

表4　膜厚比对比

表5为优化前后动态性能的对比，由表5可以看出,3组齿轮的临界转速比均小于允许临界转速比，均工作在亚临界区，满足优化设计的要求，且其临界转速比略有降低，有利于降低动载荷.

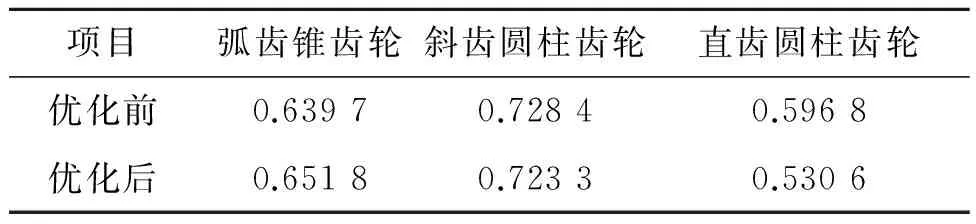
表5　动态性能对比

4 结论

1)以模糊数学为基础，结合可靠性优化设计理论，建立了模糊可靠性优化设计数学模型，求解结果使齿轮机构总体积减少，可见其优化方法的正确性、合理性.

2)综合考虑齿轮的可靠度、膜厚比、动态性能，建立了符合实际的优化数学模型，最终结果使得其综合性能得到改善，证明了此优化数学模型的正确性.

3)对于本文中复杂的数学模型，运用MATLAB遗传算法工具箱能够快速准确地求解，可见该算法简单高效，具有较好的空间适应能力和全局搜索性能.

参考文献：

[1]刘维民，夏延秋，付兴国. 齿轮传动润滑材料[M]. 北京：化学工业出版社, 2005: 68-71.

[2]张磊. 基于多目标模糊优化的减速器参数化设计[D]. 合肥: 合肥工业大学机械与汽车工程学院, 2011: 25-26.

[3]杨薇, 官德娟. 具有动态约束的齿轮传动模糊优化设计[J]. 机械传动, 2001, 25(1): 11-14.

[4]胡启国, 谢国宾, 庹奎. 蜗杆传动的可靠性优化设计研究[J]. 组合机床与自动化加工技术, 2014(7): 42-44,48.

[5]张锁怀, 万武勇, 孟旭. 风电偏航减速器四级行星传动系统可靠性优化设计研究[J]. 机械传动, 2012 (11): 48-51.

[6]蒿丽萍. 基于MATLAB的多级齿轮传动多目标可靠性优化设计研究[J]. 机械传动, 2014(1): 74-77, 91.

[7]陶振荣. 齿轮接触疲劳强度计算方法的探讨[J]. 机械设计与制造, 2007(7): 15-17.

[8]刘丽春. 斜齿圆柱齿轮的模糊可靠性设计方法[J]. 机械科学与技术, 1996, 15(3): 345-348.

[9]黄平，孟永钢，徐华. 摩擦学教程[M]. 北京：高等教育出版社, 2008: 297-298.

[10]AKBARZADEH S, KHONSARI M M. Prediction of steady state adhesive wear in spur gears using the EHL load sharing concept [J]. Journal of tribology, 2009, 131(2): 024503.

[11]NOGUEIRA I, DIAS A M, GRAS R, et al. An experimental model for mixed friction during running-in [J]. Wear, 2002, 253: 541-549.

Fuzzy Reliability Optimization Design of Gear Transmission Mechanism under Multi-specification Restriction

HU Qiguo，XIE Guobin，LUO Tianhong，TUO Kui

(College of Mechatronics and Automotive Engineering,Chongqing Jiaotong University,Chongqing 400074, China)

Abstract:In view of the problem of the gear transmission optimization design, based on the integration of fuzzy mathematics and reliability optimization design theory, a mathematic model of reliability optimization design of the mud-pump gear transmission mechanism was built with its stress and intensity obeyed certain probability distributions, when the film thickness ratio and critical speeds ratio ware put into constraint. The global optimization result was found by using GA toolbox in Matlab. The optimal results show that the comprehensive performance of the gear transmission is improved efficiently, and the correctness and applicability of that optimization method is proved, hence it provides a new reference for the gear transmission optimization design.

Key words:gear transmission; multi-specification restriction; fuzzy reliability; optimization design

收稿日期:2015-03-20；

修订日期：2015-05-10

基金项目：国家自然科学基金资助项目(51375519)；重庆交通大学研究生创新基金资助项目(20130109)

作者简介:胡启国(1968—)，男，重庆人，重庆交通大学教授，博士，主要从事机械可靠性及机械系统动力学的研究，E-mail：swpihqg@126.com.

文章编号:1671-6833(2016)01-0034-06

中图分类号：TH132.41

文献标志码：A

doi:10.3969/j.issn.1671-6833.201504038

引用本文:胡启国，谢国宾，罗天洪,等.多指标约束下齿轮传动机构模糊可靠性优化设计[J].郑州大学学报(工学版)，2016，37(1)：34-39.