可见和近红外透射光谱结合区间偏最小二乘法(iPLS)用于橄榄油中掺杂煎炸老油的定量分析

冼瑞仪， 黄富荣*， 黎远鹏， 潘莎莎， 陈 哲， 陈振强， 汪 勇

1. 暨南大学光电工程系， 广东 广州 510632

2. 暨南大学食品科学与工程系， 广东 广州 510632

可见和近红外透射光谱结合区间偏最小二乘法(iPLS)用于橄榄油中掺杂煎炸老油的定量分析

冼瑞仪1， 黄富荣1*， 黎远鹏1， 潘莎莎1， 陈 哲1， 陈振强1， 汪 勇2

1. 暨南大学光电工程系， 广东 广州 510632

2. 暨南大学食品科学与工程系， 广东 广州 510632

为探寻一种快速可靠的分析方法用于橄榄油中掺杂煎炸老油含量的测定， 实验采用可见和近红外透射光谱分析技术结合区间偏最小二乘法(interval partial least squares, iPLS)、 联合区间偏最小二乘法(synergy interval partial least squares, SiPLS)和反向区间偏最小二乘法(backward interval partial least squares, BiPLS)， 对掺杂不同含量煎炸老油的橄榄油建模分析， 并对不同模型比较优选。 采集样品400～2500 nm范围内的光谱， 对光谱数据进行Savitzky-Golay(SG)平滑去噪。 剔除奇异样本后， 采用sample set partitioning based on joint X-Y distance(SPXY)法划分样本集， 以不同的iPLS优选建模区域， 建立煎炸老油含量预测模型。 结果表明： 对掺杂不同含量煎炸大豆油的橄榄油， 采用划分20个区间， 选择2个子区间[4, 16]建立的SiPLS模型预测效果最好， 相关系数(Rp)达0.998 9， 预测均方根误差(RMSEP)为0.019 2。 对掺杂不同含量煎炸花生油的橄榄油， 采用划分20个区间， 选择2个子区间[2, 16]组合建立的SiPLS和BiPLS模型具有相同的预测效果， 预测均方根误差(RMSEP)为0.0120， 均优于iPLS模型。 此外， 与SiPLS模型相比， BiPLS模型运算量少， 速度快。 由此可见， 基于掺杂油样品的可见和近红外透射光谱， 分别采用组合区间偏最小二乘法(SiPLS)和反向区间偏最小二乘法(BiPLS)优选建模光谱区域， 可以对橄榄油中掺杂煎炸大豆油和煎炸花生油含量进行准确测定。 而且， 实验过程无需对掺杂油样品进行预处理， 无环境污染， 操作简单， 快速无损。

可见和近红外透射光谱； 区间偏最小二乘法； 掺伪； 煎炸老油； 定量分析

引 言

橄榄油原产于地中海一带， 被誉为“液体黄金”、 “植物油皇后”、 “地中海甘露”等， 深受消费者喜爱。 但是， 橄榄油生产条件严苛， 产量不足以应对不断增长的消费需求。 因此， 市场上存在不少的橄榄油掺伪现象， 特级初榨橄榄油多次被曝光掺杂了大量低价橄榄油和其他劣质油。

煎炸老油是一种常见的劣质油， 各种快餐店、 小吃店甚至个人家庭中都可能产生。 食用油在反复高温煎炸过程中， 油脂与空气中的氧和食物携带的水分发生了氧化、 聚合、 分解和水解等反应， 产生一系列可能对人体有害的醛、 酮、 酸、 内酯等化合物[1]。 一些生产经营者为获得高利润， 常将此类劣质油脂回收并以一定比例掺进合格食用油中， 尤其是高价食用油， 如橄榄油。 此种掺伪行为， 不仅造成了食用油市场混乱， 也损害了消费者的权益。 因此， 需要一种快速有效的食用油掺伪检测方法辅助政府监管。

据已有文献报道， 目前尚无公认的， 有效简单， 可以测定合格食用植物油中掺杂煎炸老油含量的方法。 对于煎炸老油等劣质油的研究， 相对而言， 关注油的品质变化及其食用安全性[2-4]、 分类检测[5-6]的更多， 对其在合格食用油中掺杂含量的研究报道较少。 对于食用油掺伪， 传统的检测方法主要有感官评价、 理化方法、 色谱法、 核磁共振法等。 然而， 感官评价法的主观性强， 理化方法对于理化性质相近的油脂难以有效区分； 色谱法和核磁共振法不但仪器昂贵， 而且操作复杂、 耗时， 需要专门的实验人员。

近红外光谱分析作为一种新型的分析技术， 不仅能提供丰富的定性和定量信息， 而且具有快速无损、 操作简便的特点。 通过近红外光谱， 可以得到样品中大量有机分子含氢基团的特征信息， 所以能同时检测多种有机分子。 近几年来备受关注， 现已在农业、 食品、 医药等领域获得应用[7-9]。 为提高预测准确性， 近红外光谱的分析中常采用区间偏最小二乘法(iPLS)， 优选建模的光谱区域[10-11]。 组合iPLS和反向iPLS， 是iPLS的延伸， 也逐渐获得应用[12]。

本实验以掺入不同含量煎炸大豆油和煎炸花生油的特级初榨橄榄油为研究对象， 采用可见和近红外光谱分析技术结合(iPLS)， 对掺杂煎炸老油的橄榄油进行建模分析， 为快速检测橄榄油中掺杂煎炸老油的含量提供一种有效的方法。

1 实验部分

1.1 样品制备

实验收集了来自澳大利亚、 意大利、 希腊、 西班牙等4个国家共7个品牌的特级初榨橄榄油， 以及中国国产的福临门大豆油和金龙鱼花生油。 大豆油主要通过大豆种子溶剂浸出而获得， 是世界上产量最多的油脂。 花生油具有独特的花生气味和风味， 可直接用于制造起酥油， 也是良好的煎炸油， 在中国普遍食用。 各原油的详细信息见表1。

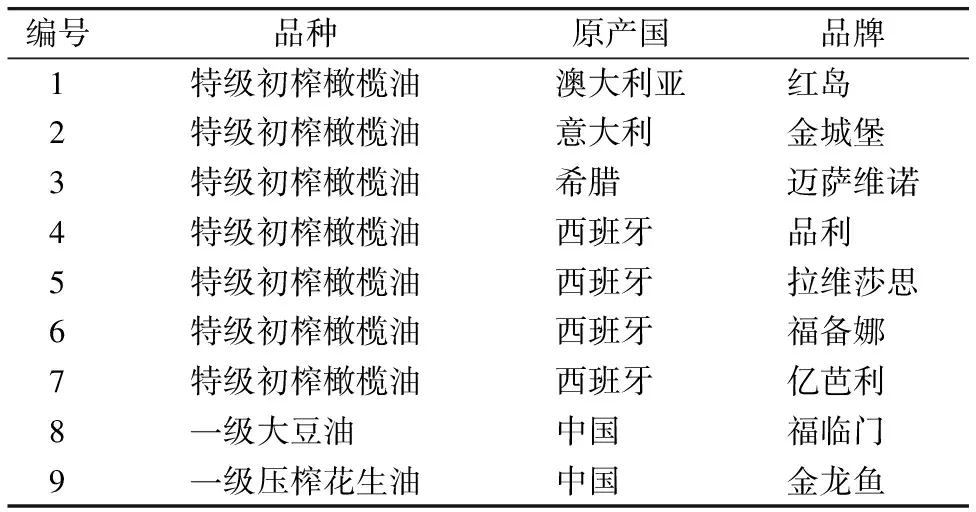
表1 实验中使用的油

从外界获得的煎炸老油成分相对复杂且真实性有待考察， 所以实验室制备煎炸老油。 使用汇利HY-83单缸双筛台式电炸炉油炸锅， 煎炸油温控制在179 ℃， 此温度可满足一般淀粉类和肉类的煎炸。 分别对大豆油和花生油煎炸10次， 每次持续30 min， 并投入相同质量的土豆条模拟日常煎炸情境。 待前一次煎炸的油温恢复至常温并维持10 min后， 才进行下一次煎炸。 经过10次煎炸后的大豆油和花生油为备用的煎炸老油样品。

将制备的煎炸大豆油(花生油)与橄榄油按体积比1∶9～9∶1混合， 得到掺杂煎炸大豆油(花生油)的橄榄油混合油样各63个。 7个特级初榨橄榄油的纯油样亦作为掺杂煎炸老油含量分析模型的样品， 则橄榄油中掺杂的煎炸老油含量范围为0～0.9。

1.2 光谱采集

实验采用丹麦福斯公司XDS Rapid Content光栅型近红外光谱分析仪及其透射附件， 光谱采集范围为400～2 500 nm， 探测器为Si(400～1 100 nm)、 PbS(1 100～2 500 nm)。

采集掺杂煎炸老油的橄榄油样品和特级初榨橄榄油样品光谱， 每隔2 nm采样一次， 获得400～2 500 nm范围的光谱。 所有油样的光谱数据均采集3次取平均， 得到特级初榨橄榄油光谱7个， 橄榄油分别掺杂煎炸大豆油和煎炸花生油的混合油样品光谱各63个， 共133个光谱。

1.3 划分样品集

目前， 样品的选择方法主要有random sampling(RS)法， Kenard-Stone(KS)法， Duplex法以及sample set partitioning based on joint X-Y distance(SPXY)法。 本实验采用SPXY法进行样品集划分。

SPXY法[13]由Galvã等提出， 能有效应用于近红外光谱定标模型的分析， 是基于KS法的样品划分方法。 与KS法相比， SPXY法计算样品空间距离时同时考虑x变量和y变量。x变量的空间距离计算公式与KS法相同， 见式(1)。y变量的空间距离计算公式， 见式(2)。

(1)

(2)

SPXY法的逐步选择过程与KS法相似， 只是用dxy(p,q)代替了dx。dxy(p,q)是经标准化的xy距离， 使样品在x空间和y空间具有相同的权重， 其计算公式见式(3)。

(3)

1.4 iPLS

iPLS是目前较为常用的优选特征光谱区间的化学计量学方法， 由Nφrgaard等[14]提出。 在整个光谱范围内划分为n个等分区间， 在各子区间内以不同的因子数建立独立的偏最小二乘(PLS)回归模型。 计算各子模型的交互验证均方根误差(RMSECV)， 作为模型评判标准。 对于同一个子区间， 当RMSECV最小时， 所采用的因子数为最优因子数， 以此建立各子区间的局部最优模型。 比较各子区间的局部最优模型和全光谱模型， 选择其中RMSECV最小的独立子区间模型， 对应区间为优选的建模区间。

联合区间偏最小二乘法(SiPLS)是iPLS的一个延伸， 弥补了iPLS单一区间建模的缺点。 与iPLS相似， 根据设定的子区间划分数将区间等距划分。 后依据指定的组合区间个数， 将各子区间随机组合。 对每组组合区间建立PLS回归模型， 并以列表形式展现各组合区间的模型信息， 以RMSECV最小的模型对应的组合区间作为优选的建模区间。

反向区间偏最小二乘法(BiPLS)也是在iPLS的基础上发展而来， 由Nφrgaard等提出。 将整个光谱等分为n个子区间数， 每次排除一个区间， 使得在(n-1)个子区间内建模， 模型的RMSECV最小。 依次类推， 直至仅剩一个子区间。 最后选择RMSECV最小的区间组合作为建模区间， 亦弥补了iPLS单一区间建模的缺点。

1.5 模型评价参数

交互验证均方根误差(RMSECV)、 预测均方根误差(RMSEP) 是建模的重要评价参数， 模型相关系数r辅以参考， 模型的优选以RMSEP作为最终指标。 RMSECV、 RMSEP以及R的计算公式如下：

(4)

(5)

(6)

2 结果与讨论

2.1 可见和近红外光谱

图1是经SG平滑预处理后， 特级初榨橄榄油和掺杂煎炸油的橄榄油混合油的可见和近红外透射光谱图， 对应的(a)掺杂煎炸油为大豆油， (b)则为花生油。 实验获取的光谱除了包含样品的有用信息外， 常叠加了各种随机噪声， 可采用数学校正。 SG平滑算法简单， 是常用的降噪方法。 因此， 对原始光谱进行三阶SG平滑， 平滑窗口为7。

2.2 奇异样品剔除及样品集划分

奇异样品识别是建立稳健模型的基础。 基于蒙特卡罗交互检验(MCCV)的奇异样品筛选法与传统方法相比， 具有较高的识别奇异样品的能力。 设定最大主成分数为5， 用蒙特卡罗随机取样法(MCS)取80%的样品作为定标集建立偏最小二乘(PLS)回归模型， 剩余部分做预测集， 循环500次， 求各样品的预测均值(MEAN)和预测误差标准差(STD)， 并作MEAN-STD图以直观寻找离群样品， 见图2。 可以看到， 大部分样品聚集在一个区域， 而(a)中第47个样品和(b)中第57个样品明显偏离主体样品， 因此将其作为奇异样品剔除。

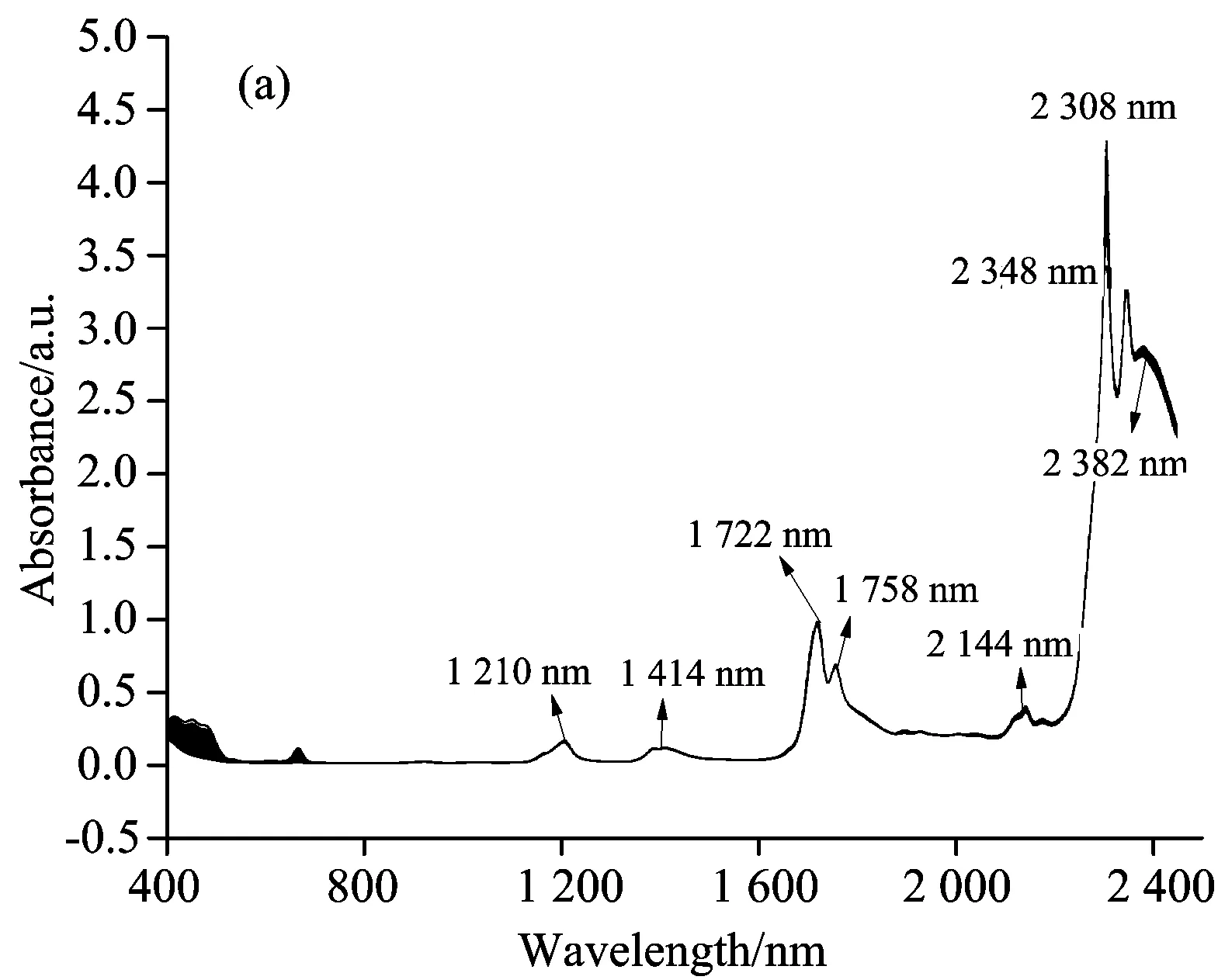
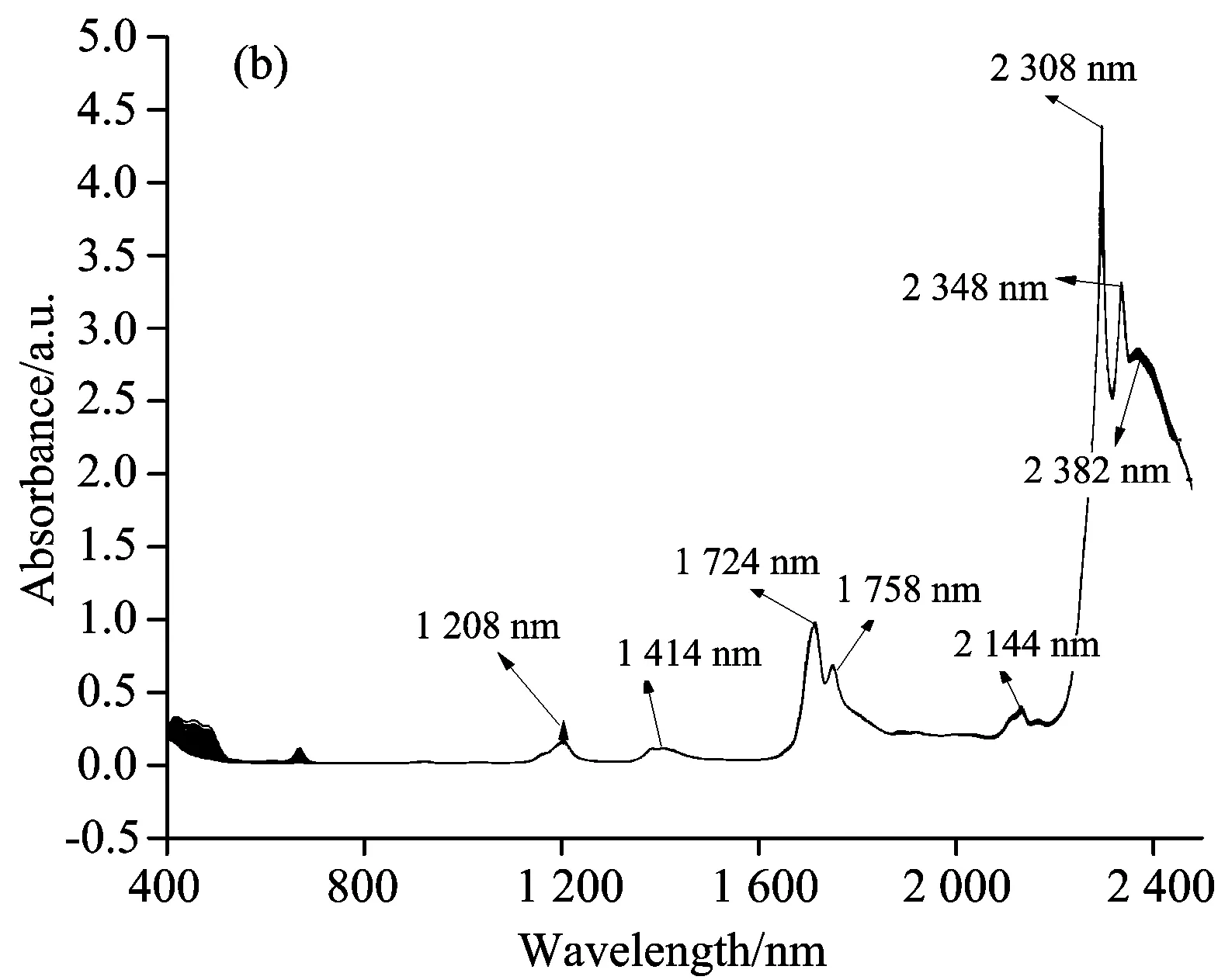
图1 特级初榨橄榄油掺杂煎炸大豆油(a)和煎炸花生油(b)的可见和近红外透射光谱图

Fig.1 Visible/near infrared transmission spectra of (a) deep-frying soybean oil adulterated virgin olive oil, (b) deep-frying peanut oil adulterated virgin olive oil

模型的预测集样品一般都要求是独立的， 不能从原有的定标样品集中选择一些样品应用于预测模型。 因此， 实验中对经过奇异样品剔除后的剩余样品， 采用SPXY法分别选取49个样品作为校正集， 20个作为独立预测集。

2.3 煎炸老油含量预测模型

2.3.1 iPLS模型

将经过预处理的全光谱， 划分为10， 15， 20和25个子区间， 分别对全光谱和各子区间建立PLS回归模型， 比较模型的RMSECV。 确定不同子区间划分下， RMSECV最小的回归模型。 以对应的光谱区间建立掺杂油含量分析的定标模型， 并以独立的预测集进行验证， 比较各预测模型的RMSEP。

由表2中各模型的RMSEP值， 可以得知， 对于掺杂煎炸大豆油和花生油的iPLS含量分析模型， 分别采用划分为10个子区间， 选择第8个子区间建模和划分25个子区间， 选择第22个子区间建模的预测效果最好。 两模型的RMSEP值分别为0.020 4和0.014 4。

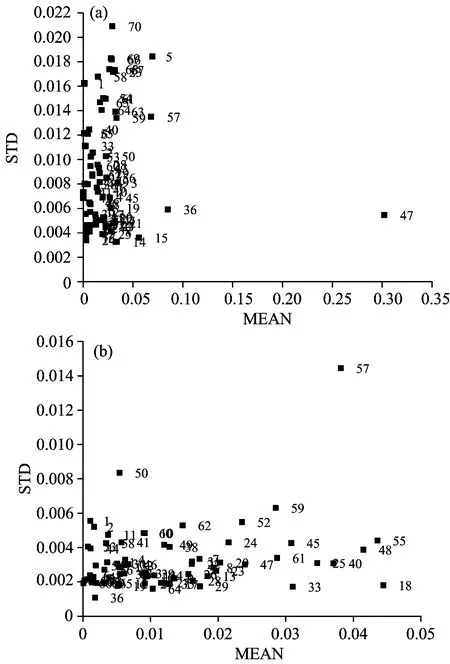
图2 特级初榨橄榄油掺杂煎炸大豆油(a)和煎炸花生油(b)样品的预测均值和均方根误差关系图

Fig.2 Mean value and standard deviation of prediction error of (a) deep frying soybean oil adulterated virgin olive oil, (b) deep frying peanut oil adulterated virgin olive oil

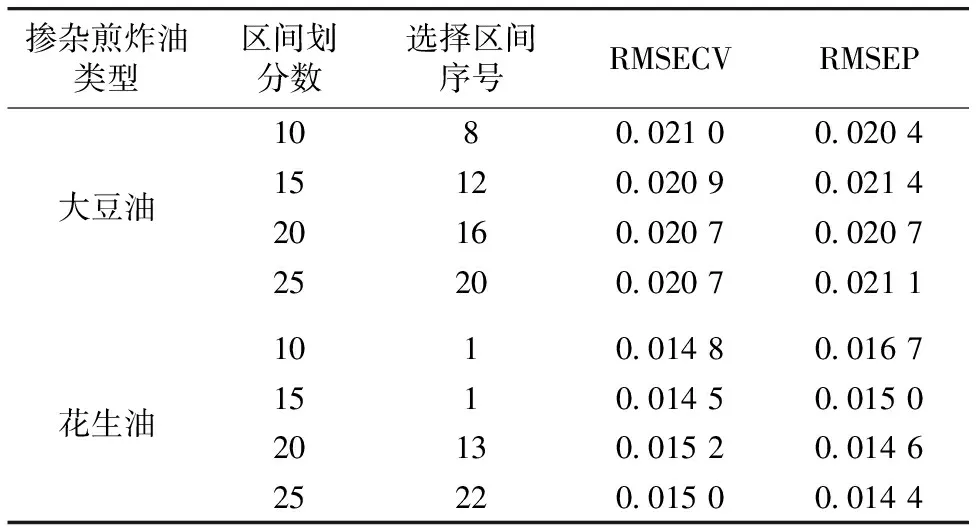
表2 划分10， 15， 20， 25个子区间的iPLS优选模型

2.3.2 SiPLS模型

联合区间偏最小二乘法(SiPLS)将同一次区间划分中的若干个子区间联合起来， 以联合区间模型的RMSECV值作为建模区间优选的评价标准， 克服了区间偏最小二乘(iPLS)单一区间建模的缺点。 但各子区间的联合是随机组合， 组合方式多样， 因此计算量大。

在400～2 500 nm全谱范围， 划分为10， 15， 20和25个子区间， 再分别进行2个、 3个子区间组合运算， 建立各组合区间的PLS回归模型， 比较各组合模型的RMSECV， 筛选最佳区间组合。 以此组合区间建立掺杂油含量分析的定标模型， 并进行验证。

由表3可以看出， 对于掺杂煎炸大豆油的含量分析模型， 当全光谱划分为20个区间， 两个区间[4, 16]组合时， 建立的SiPLS模型预测效果最好， RMSEP值0.019 2， 选择波长范围为715～820和1 975～2 080 nm。 而对于掺杂煎炸花生油， 全谱划分为20个子区间， 两个区间[2, 16]组合建模时RMSEP最小0.012 0， 建模波长为505～610和1 975～2 080 nm。

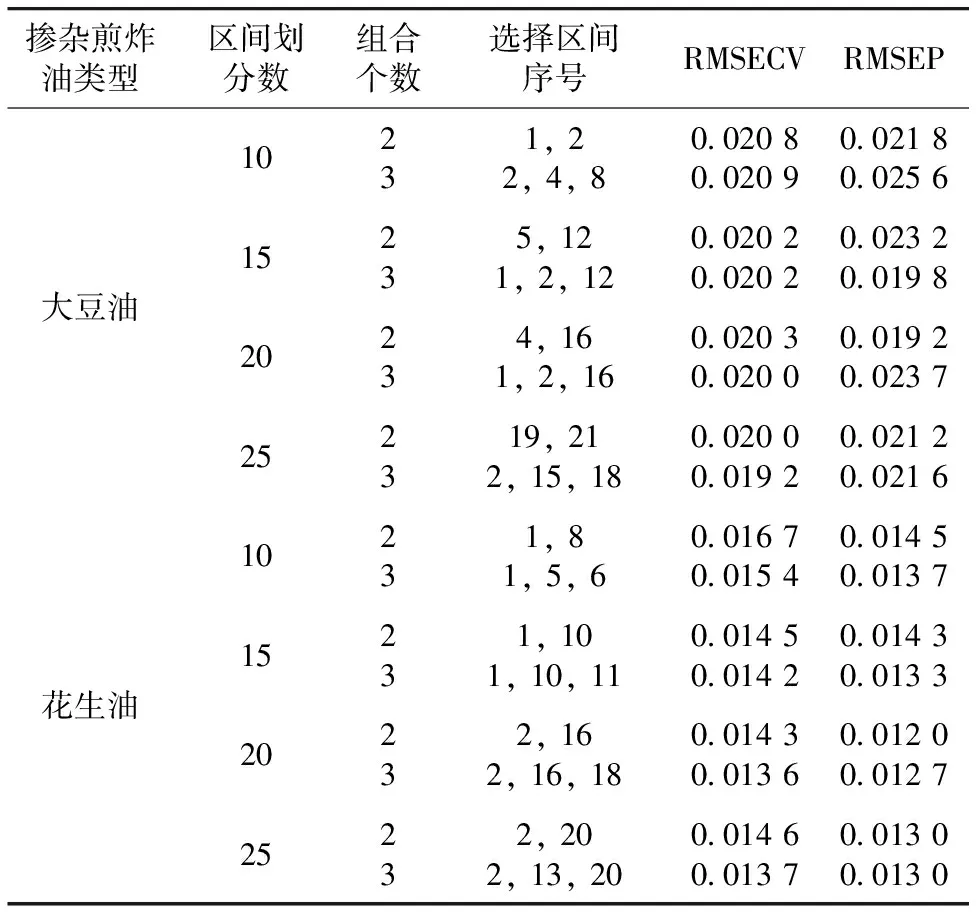
表3 不同组合区间数的SiPLS优选模型

2.3.3 BiPLS模型

反向区间偏最小二乘法(BiPLS)是克服iPLS只能单一区间建模缺点的另一种改进方法。 与SiPLS相比， 运算量减少， 运算速度加快。

将400～2 500 nm范围的光谱划分为10， 15， 20， 25个子区间， 分别采用BiPLS法进行光谱变量优选， 以优选的光谱区间建立掺杂油含量分析的定标模型并进行预测， 各预测结果见表4。

由表4可见， 掺杂煎炸大豆油的含量分析模型在全谱划分为10个子区间， 选择第8个子区间建模时的预测效果最好， RMSEP值为0.020 4， 选择了波长段1 870～2 080 nm建模。 对于掺杂煎炸花生油的含量分析， 划分20个子区间， 选取[2, 16]子区间组合， 建立的BiPLS模型的RMSEP值最小， 为0.012 0。 选择的建模波长为505～610和1 975～2 080 nm。

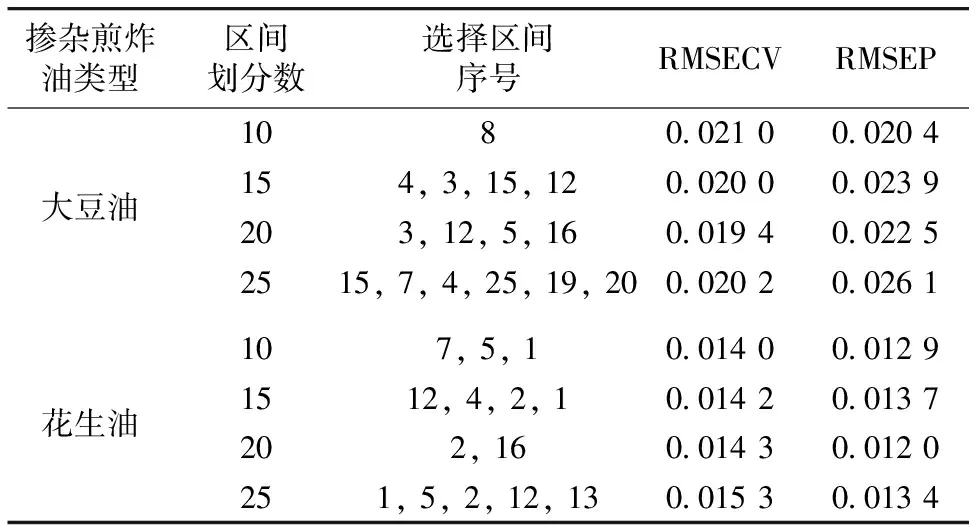
表4 划分10， 15， 20， 25个子区间的BiPLS优选模型

2.4 预测模型优选

将上述不同偏最小二乘法优选光谱区间建立的模型进行比较， 各模型预测结果， 见表5。

表5 不同光谱区间建模的优选模型

橄榄油中掺杂煎炸大豆油的预测分析， 选取的iPLS模型与BiPLS模型的建模区间相同， 定标模型与预测模型的相关指标也相同。 BiPLS模型并没有优选更多的波长变量， 仍是单一区间的建模。 最终比较得到的最优模型是区间划分数为20， 选择组合区间[4, 16]建立的SiPLS模型， 其RMSECV和RMSEP均低于iPLS模型和BiPLS模型。 RMSEP和Rp分别为0.0192和0.998 9。

橄榄油中掺杂煎炸花生油的预测分析， 选取的SiPLS模型与BiPLS模型的建模区间相同， 定标模型与预测模型的相关指标也相同。 另外， 两模型的RMSECV和RMSEP值均小于iPLS模型， 分别为0.014 3和0.012 0， 预测模型相关系数Rp达0.999 3。 不过， 从运算量和运算速度上比较， BiPLS模型比SiPLS模型运算量更少， 速度更快。

本实验最后选用SiPLS模型用于橄榄油中掺杂煎炸大豆油含量的预测， 模型子区间数为20， 选择区间[4, 16]， 对

应波长范围715～820和1 975～2 080 nm， 其预测效果见图3(a)。 选用BiPLS模型用于橄榄油中掺杂煎炸花生油含量的预测， 全谱划分为20个子区间， 选择区间[2, 16]， 对应波长范围505～610和1 975～2 080 nm， 其预测效果见图3(b)。

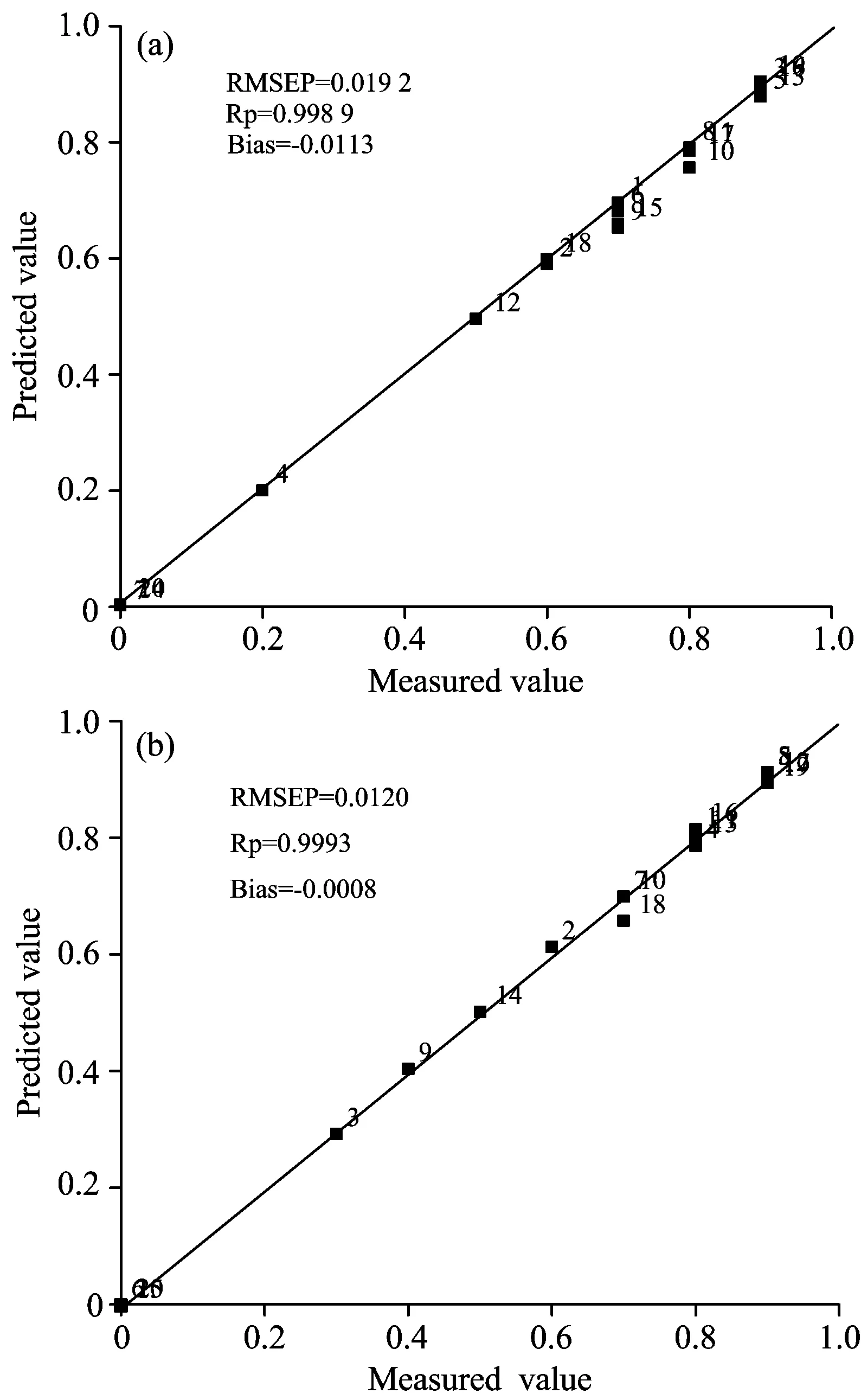
图3 特级初榨橄榄油掺杂煎炸大豆油的SiPLS模型(a)和掺杂煎炸花生油的BiPLS模型(b)的最优预测结果

Fig.3 Optimal results of prediction models obtained by (a) SiPLS for deep frying soybean oil adulterated virgin olive oil, (b) BiPLS for deep frying peanut oil adulterated virgin olive oil

3 结 论

基于可见和近红外透射光谱， 采用不同的区间偏最小二乘法建模并比较选优。 最终分别选定联合区间偏最小二乘法和反向区间偏最小乘法所建模型用于橄榄油掺杂煎炸大豆油和煎炸花生油的含量预测。 两个模型都有较好的预测效果， 对煎炸老油掺杂含量进行了有效的定量分析， 并且无需对掺杂油样品做处理， 操作简单， 耗时短。 为橄榄油掺杂煎炸老油的含量测定提供了一种较为快速准确的方法， 也为合格食用植物油中掺杂其他不良油脂的检测提供参考。

[1] Clark W L, Serbia G W. Food Technology, 1991, 45(2): 84.

[2] Freire P C M, Lobo L C B, Freitas G D, et all. Food Science and Technology, 2013, 33(3): 569.

[3] Weisshaar Rüdiger. European Journal of Lipid Science & Technology, 2014, 116(6): 716.

[4] Sebastian A, Ghazani S M, Marangoni A G. Food Research International, 2014, 64: 420.

[5] Torrecilla J S, Cancilla J C. Journal of Food Engineering, 2013, 118(4): 400.

[6] Wrona M, Pezo D, Nerin C. Food Chemistry, 2013, 141(4): 3993.

[7] Ni Yongnian, Mei Minghua, Serge Kokot. Chemometrics and Intelligent Laboratory Systems, 2011, 105(2): 147.

[8] Galtier O, Abbas O, Le Dréau Y, et al. Vibrational Spectroscopy, 2011, 55(1): 132.

[9] Rohman Abdul, Nugroho Ardi, Lukitaningsih Endang, et al. Applied Spectroscopy Reviews, 2014, 49(8): 603.

[10] Alberto Villar, Santiago Fernández, Eneko Gorritxategi, et al. Chemometrics and Intelligent Laboratory Systems, 2014, 130(2): 68.

[11] Julia Kuligowski, David Carrión, Guillermo Quintás, et al. Food Chemistry, 2012, 131(1): 353.

[12] Niu Xiaoying, Zhao Zhilei, Jia Kejun, et al. Food Chemistry, 2012, 133(2): 592.

[13] Roberto Kawakami Harrop Galvão, Mário César Ugulino Araujo, Gledson Emídio José, et al. Talanta, 2005, 67(4): 736.

[14] Nφrgaard R, Saudland A, Wagner J, et al. Applied Spectroscopy, 2000, 54(3): 413.

[15] Workman Jerry, Weyer Jr Lois. Practical Guide to Interpretive Near-Infrared Spectroscopy(近红外光谱解析实用指南). Translated by CHU Xiao-li， XU Yu-peng， TIAN Gao-you(褚小立， 许育鹏， 田高友， 译). Beijing: Chemical Industry Press(北京： 化学工业出版社), 2009. 221.

Quantitative Analysis of Deep-Frying Oil Adulterated Virgin Olive Oil Using Vis-NIR Spectroscopy with iPLS

XIAN Rui-yi1， HUANG Fu-rong1*， LI Yuan-peng1， PAN Sha-sha1， CHEN Zhe1， CHEN Zhen-qiang1， WANG Yong2

1. Opto-electronic Department of Jinan University， Guangzhou 510632， China

2. Food Science and Engineering Department of Jinan University， Guangzhou 510632， China

To explore a rapid and reliable method for quantitative analysis of deep-frying oil adulterated virgin olive oil, visible and near infrared(Vis-NIR) spectroscopy and three improved partial least squares methods, including interval Partial Least Squares (iPLS), synergy interval partial least squares (SiPLS) and backward interval partial least squares (BiPLS) were employed to establish predicting models of doping content based on virgin olive oil adulterating different levels and different types of deep-frying oil. And the models were compared in order to choose the best one. The Vis-NIR spectroscopy ranged from 400 to 2 500 nm was obtained directly from the adulterated samples, and the spectroscopic data was preprocessed with Savitzky-Golay (SG). Then, the samples were divided into calibration set and test set by Sample Set Partitioning based on Joint X-Y Distance (SPXY) after rejecting the odd samples. At last, the predicting models of doping content were built by using different interval partial least squares methods. The results showed that the optimal model for predicting the doping content of deep-frying soybean oil in virgin olive oil was obtained with SiPLS method that separated the whole spectra into 20 intervals and combined the fourth and the sixteenth intervals. The SiPLS model had correlation coefficient (r) of 0.998 9 and root mean standard error of prediction (RMSEP) of 0.019 2. In addition, for deep-frying peanut oil adulterated virgin olive oil, the SiPLS and BiPLS models with interval 2 and interval 16 which the whole spectra was separated into 20 intervals, had same results. The RMSEP was 0.012 0, lower than iPLS model. Moreover, compared to SiPLS method, BiPLS method saved computation and was more efficient. Overall, through selecting the effective wavelength range, SiPLS method and BiPLS method could accurately predict the doping content of deep-frying oil in virgin olive oil based on its’ Vis-NIR spectroscopy. In addition, this fast and nondestructive experiment doesn’t need sample pretreatment with advantages of no environment pollution, easy operation.

Vis-NIR spectroscopy; Interval partial least squares regression (iPLS); Adulteration; Deep-frying oil; Quantitative analysis

Apr. 8, 2015; accepted Aug. 21, 2015)

2015-04-08，

2015-08-21

国家自然科学基金项目(31371785)， 广东省战略新兴产业核心技术攻关项目(2012A032300016)， 高等学校博士学科点专项科研基金项目(20124401120005)， 广东省自然科学基金项目(S2011040001850)， 广东高校优秀青年创新人才培养计划项目(LYM11026)和中央高校基本科研业务费专项资金项目(21612436， 21612353)资助

冼瑞仪， 女， 1992年生， 暨南大学光电工程系本科生 e-mail： ruiprovence@163.com *通讯联系人 e-mail: furong_huang@163.com

O433.4

A

10.3964/j.issn.1000-0593(2016)08-2462-06

*Corresponding author