基于反演法的某制导迫弹鲁棒自适应控制器设计
2016-06-15廖海波
廖海波
(安徽神剑科技股份有限公司,合肥 230601)
基于反演法的某制导迫弹鲁棒自适应控制器设计
廖海波
(安徽神剑科技股份有限公司,合肥230601)
摘要:设计了一种基于反演法的鲁棒自适应控制器,以解决制导迫弹在飞行中存在的气动参数不确定和未建模误差等问题,在设计过程中通过带有σ修正的参数自适应律对系统中的不确定参数进行在线估计,针对模型中的未建模误差,采用鲁棒函数抵消,在反演法的推导过程中,加入了一阶低通滤波器,得到虚拟控制量的微分,消除了传统反演法中的“项数膨胀”难题,并利用李雅普诺夫函数证明了该闭环系统为半全局稳定的。该设计方法放宽了对不确定项的限制,仿真结果证明了该方法的有效性。
关键词:制导迫弹;反演法;自适应控制;鲁棒控制
制导迫弹是当前国家重点发展的对象,能够为营级部队提供可靠的火力支援。制导迫弹借助于常规迫榴炮发射平台发射,通过制导控制系统引导迫弹命中目标[1]。制导迫弹外界环境干扰较为复杂,并且其运动模型是一个非线性、多变量的系统,因此模型中存在较大误差,主要集中在气动参数误差和未建模动态。系统中不确定性会严重影响整个系统的性能,采用传统的线性控制理论难以取得较好的控制效果,应寻找更为有效的非线性控制设计方法[2]。
反演法在20世纪90年代被提出,它能够有效处理系统的不确定性和未知参数,其思想为结合李雅普诺夫函数逐层设计虚拟控制变量,并一直“后退”到整个系统,直到完成全部控制律的设计[3-4]。它能够避免对消系统中有用的非线性,以镇定和跟踪为其追求的目标。但是在推导过程中,会导致“项数膨胀”,使控制器难以工程实现。为解决“项数膨胀”问题,文献[5]中提出了动态面控制方法,在设计过程中引入一阶低通滤波器,降低了控制律的复杂度,解决了该难题。国外学者在文献[5]中的基础上,将鲁棒自适应与反演法相结合,为多种飞行器设计了控制器,文献[6]基于动态面为小灵巧炸弹设计了反演控制器,但当系统存在气动参数不确定性及未建模动态时,控制器效果较差,文献[7]中将反演法与滑膜控制结合为BTT导弹设计了自适应控制器,有效地补偿了系统不确定性的影响,但该方法要求较为苛刻,要求系统不确定性已知。
本研究将鲁棒、自适应、反演法相结合,为带有不确定性的制导迫弹模型设计了一种鲁棒自适应控制器。引入了一类鲁棒函数来补偿系统的建模误差,并通过自适应律对不确定上界进行估计,通过低通滤波器克服“项数膨胀”的难题,针对气动参数的不确定性,采用自适应律对其进行在线估计,有效地利用了已知信息。
1模型建立
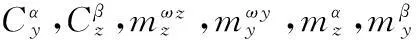
(1)
式中
xi=(x1,x2,x3,x4)=(α,β,ωz,ωy)

2鲁棒自适应控制律设计

1)俯仰通道控制系统设计

(2)
(3)
对S1求导可得
(4)

(5)
滤波器输出误差如式(6)所示
(6)
(7)
由此式(4)可以改写为
(8)
该控制系统的误差项有4部分组成,迫弹攻角和目标攻角的跟踪误差,滤波器输出误差,气动参数估计误差以及系统未建模误差,如果上述4个误差均能限制在较小范围内,则该控制系统是稳定且能够跟踪指定目标。选定李雅普诺夫函数V1并对其求导。
(9)

(10)
针对上述公式需进行部分简化,k1=2+Γ又由Young’s不等式可知
最终式(10)可改写为
(11)
为了能有效地利用已知信息,改善参数估计的精度。本文采用带σ修正的传统参数适应律。
(12)
(13)
(14)
利用
(15)
(16)
最终可推得

(17)
又由
(18)
最终可以推出

(19)
第二步对定义的第三个动态面求导
(20)
选取控制器的输入为
(21)
同理取
(22)
对传统参数适应律进行σ修正。
(23)
(24)
(25)
选取第二个李亚普诺夫函数
(26)

同理可以推出
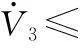
(27)
令 C1=min{2Γ,ο1r1,ο3r3,σ1T1,σ3T3,σ5T5}
可得
(28)
解式(28)可得
(29)
显然可得
(30)
由式(30)可知


最终可以证明攻角的跟踪误差、一阶低通滤波器、未建模动态及其参数估计误差有界且收敛至系统原点的一个领域内。由于引入了自适应律进行在线估计,参数不确定上限已知的限制条件得以放宽。
2)偏航通道控制系统设计
偏航通道设计过程与纵向通道较为类似,同理针对公式 第二项和第四项引入新的变量S2、S4。S2、S4分别为迫弹侧滑角和偏航角度率与目标侧滑角和目标偏航角度率之间的误差。参数适应律选取与俯仰通道类似,不再详细推导,控制器的输入选取如下:
(31)
针对1的第二项、第四项选取李雅普诺夫函数如下
(32)
令 C1=min{2Γ2,ο2r2,ο4r4,σ2T2,σ4T4,σ6T6}
故可得
(33)
显然可得
(34)
最终同理可以证明制导迫弹的偏航通道也是稳定的,且系统误差可以被限制在一个有界的范围之内。至此可以证明出制导迫弹的俯仰和偏航通道控制器均是稳定的。
通过上述推导可以看出该系统俯仰和偏航通道的控制器输入是相互耦合的。控制系统输入如下
(35)
3仿真分析
接下来以某型制导迫弹为例对所设计的控制器进行仿真,假设制导迫弹在某个特征点处速度为270 m/s,滚转角速度为2 r/s,初始攻角和侧滑角为0。系统建模误差为 E=2×sin(πT)[0.1,0.2,0.3,0.4]T,接下来对上述研究控制器进行仿真,以纵向为例进行说明。
经多次尝试控制器增益最终取为Γ=1.5,Γ2=2,o1=3,o2=4,o3=4,o4=5σ1=100,σ2=120,σ3=80,σ4=100,σ5=150,σ6=200。
图1~图2为制导迫弹跟踪指定姿态角的仿真图,由图1~图2可知仿真曲线吻合程度较高,能够准确地跟踪指定姿态角。图3为俯仰通道等效舵片角仿真图。
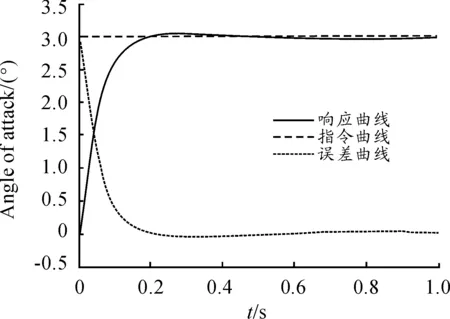
图1 制导迫弹跟踪指定攻角

图2 制导迫弹攻角跟踪正弦曲线
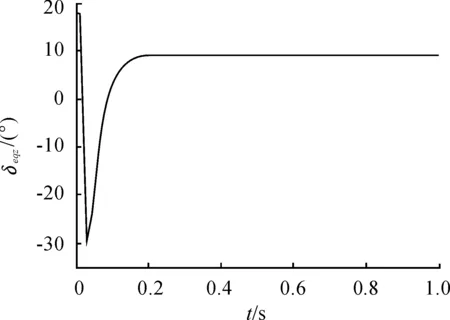
图3 俯仰等效舵偏角曲线响应图
4结束语
反演法的提出,极大地促进了非线性控制的发展,该方法的控制规律能够提供收敛的稳定的性能,并且能够保留对系统有益的非线性特性。本文在实际考虑制导迫弹飞行过程中存在气动参数不确定及未建模误差的情况下,基于反演法设计了一种鲁棒自适应控制律,通过参数自适应律对系统中的不确定参数进行在线估计,采用鲁棒函数抵消模型中的未建模误差,引入一阶低通滤波器,消除传统反演法中的“项数膨胀”难题,李雅普诺夫函数证明了该闭环系统为半全局稳定的,最后基于Matlab/Smulink的仿真验证了该设计方法的有效性。
参考文献:
[1]曹小兵,徐伊岑,王中原,等.迫弹横向脉冲控制飞行稳定性[J].弹道学报,2008,20(4):41-44.
[2]陈圣,王旭刚.制导炮弹非线性鲁棒自适应控制系统设计[J].电光与控制,2014,21(4):61-64.
[3]郭一,刘金琨.飞行器航迹倾角的自适应动态面控制[J].北京航空航天大学学报,2009,39(2):275-279.
[4]董长虹,周国杰,徐世杰.反演法在导弹非线性控制系统设计中的应用[J].航天控制,2010,28(1):3-6.
[5]SWAROOP D,HEDRICK J K,YIP P P,et al.Dynamic surface control for a class of nonlinear systems[J].IEEE Trans Automatic Control,2000,45(10):1893-1899.
[6]张志民.小灵巧炸弹BTT控制器设计与弹道仿真[D].南京:南京理工大学,2010.
[7]ZHOU J W,WEN C.Adaptive Backstepping Control of Uncertain systems[M].Berlin:Spinger-Verlag,2007.
[8]郑友胜.远程制导炮弹弹道优化设计与姿态控制方法研究[D].南京:南京理工大学,2008.
[9]钱杏芳.导弹飞行力学[M].北京:北京理工大学出社,2011.
[10]王辚,高原,范文涛.基于反演变结构方法的变外形导弹控制系统[J].探测与控制学报,2014(3):46-51.
(责任编辑周江川)
本文引用格式:廖海波.基于反演法的某制导迫弹鲁棒自适应控制器设计[J].兵器装备工程学报,2016(5):70-73.
Citation format:LIAO Hai-bo.Guided Mortar Projectile Robust Adaptive Controller Design Based on Backstepping[J].Journal of Ordnance Equipment Engineering,2016(5):70-73.
Guided Mortar Projectile Robust Adaptive Controller Design Based on Backstepping
LIAO Hai-bo
(Anhui Shenjian Technology Company Limited,Hefei 230601,China)
Abstract:A controller using robust adaptive based on backstepping was designed for guided mortar projectile with uncertain aerodynamic parameters and unmodeled dynamics.The problem of uncertain aerodynamic parameters was solved by the parameter estimator through parameter self-adaptive with σ amendatory,and the robust term was designed to solve the problem about approach error.“Explosion of complexity” which existing in traditional backstepping approach was solved by introduction of low pass filters.Finally,the closed-loop system was proved by Lyapunov function for semi-global stability and the research object was expanded to a nonlinear dynamics system.The numerical simulation shows that the proposed control system illustrates good tracking performance and robustness.
Key words:guided mortar projectile; backstepping; adaptive control; robust control
doi:【装备理论与装备技术】10.11809/scbgxb2016.05.017
收稿日期:2015-12-08;修回日期:2015-12-29
作者简介:廖海波(1976—),男(土家族),硕士,总工程师,主要从事弹箭总体设计研究。
中图分类号:TJ765.2
文献标识码:A
文章编号:2096-2304(2016)05-0070-05
