万有引力距离平方反比关系的三种不同思维层次的推导

何尧荣

摘 要：万有引力定律的建立关键是平方反比关系的确立，教材限于学生的水平只做了近似推导。本文从培养学生思维严密性的目的出发，从近似法、假设法、严密推理法等3个不同的思维层次进行了推导，不失为一种尝试，对于重点中学的学生和那些学有余力的学生，进行了有效的思维训练和拓展，对思维品质是一种很大的提升。

关键词：万有引力；平方反比；假设

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2016）5-0036-3

万有引力定律的建立是人类长期对行星运动的观察，科学记录观察数据（第谷的观察数据），并通过严格的数据分析、综合得到开普勒行星运动三大定律的基础上，牛顿借助运动定律，通过严格推理，地、月检验而得。借助万有引力发现的这个载体，挖掘其中的思维、思想，是对学生思维严密性培养的好素材。本文拟从3个高度不同的思维层面，还原物理学家在万有引力大小与距离平方成反比关系发现的思维过程，以期对学生思维品质的提升起到一定的促进作用。

开普勒在第谷几十年对行星观察数据的基础上，通过科学的方法总结得到了行星运动三大定律：

第一定律：所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上。

第二定律：对于任意一个行星来说，它与太阳的连线在相等的时间内扫过相等的面积。

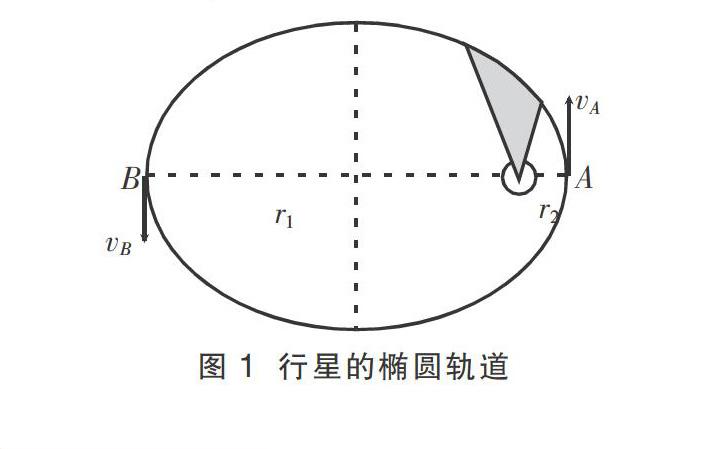
如图1所示，Δt内行星和太阳的连线所扫过的面积ΔS=r·rΔθ=r2Δθ。

1 普通高中课程标准实验教科书物理必修2中的近似推理[1]

假设行星绕太阳的运动是圆周运动，根据开普勒行星运动第一、第二定律，行星以太阳为圆心做匀速圆周运动，太阳对行星的引力就等于行星做匀速圆周运动的向心力。

这种推理一般学生都能理解和接受，但总有一种近似的感觉，似乎万有引力定律是个近似定律。

2 假设推理

根据开普勒行星运动第一定律，行星绕太阳做椭圆轨道运动，任何曲线运动都是变速运动，受力都不平衡，因而行星绕太陽运动时受力一定不平衡，必会受到周围天体对它的力的作用，在太阳系中可忽略其他行星的作用，认为其所受合力就是太阳对它的引力作用。并且，物体做曲线运动时在短时间内都可看成是在一小段圆弧上的圆周运动。假设行星所受太阳对它的引力与距离的n次方成正比，即设：F=krn。

行星运动到近日点和远日点时，由开普勒行星运动第二定律得：速度分别为最大值和最小值。因而，只有向心加速度，没有切向加速度，由向心力公式及牛顿第二定律得：

万有引力定律的建立是人类长期对行星运动的观察，科学记录观察数据（第谷的观察数据），并通过严格的数据分析、综合得到开普勒行星运动三大定律的基础上，牛顿借助运动定律，通过严格推理，地、月检验而得。借助万有引力发现的这个载体，挖掘其中的思维、思想，是对学生思维严密性培养的好素材。本文拟从3个高度不同的思维层面，还原物理学家在万有引力大小与距离平方成反比关系发现的思维过程，以期对学生思维品质的提升起到一定的促进作用。

开普勒在第谷几十年对行星观察数据的基础上，通过科学的方法总结得到了行星运动三大定律：

第一定律：所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上。

第二定律：对于任意一个行星来说，它与太阳的连线在相等的时间内扫过相等的面积。

如图1所示，Δt内行星和太阳的连线所扫过的面积ΔS=r·rΔθ=r2Δθ。

在开普勒行星运动三大定律的基础上，万有引力定律的发现过程中，分别经历了近似推理，假设推理和严格的数理推理及地、月检验等过程，体现了物理学的研究方法，对学生是一个不可多得的教学素材。

1 普通高中课程标准实验教科书物理必修2中的近似推理[1]

假设行星绕太阳的运动是圆周运动，根据开普勒行星运动第一、第二定律，行星以太阳为圆心做匀速圆周运动，太阳对行星的引力就等于行星做匀速圆周运动的向心力。

这表明：太阳对不同行星的引力，与行星的质量成正比，与行星和太阳间距离的二次方成反比。

这种推理一般学生都能理解和接受，但总有一种近似的感觉，似乎万有引力定律是个近似定律。

2 假设推理

根据开普勒行星运动第一定律，行星绕太阳做椭圆轨道运动，任何曲线运动都是变速运动，受力都不平衡，因而行星绕太阳运动时受力一定不平衡，必会受到周围天体对它的力的作用，在太阳系中可忽略其他行星的作用，认为其所受合力就是太阳对它的引力作用。并且，物体做曲线运动时在短时间内都可看成是在一小段圆弧上的圆周运动。假设行星所受太阳对它的引力与距离的n次方成正比，即设：F=krn。

行星运动到近日点和远日点时，由开普勒行星运动第二定律得：速度分别为最大值和最小值。因而，只有向心加速度，没有切向加速度，由向心力公式及牛顿第二定律得：

这种推理巧妙地利用假设法，抓住特殊位置进行推理，曲线运动在短时间内可以看作圆弧运动，进行了思维拓展，开阔学生的思维，享受到了思维大餐，但还是有一种小聪明和近似的感觉。

3 极坐标法进行严格推理

如图2所示，取太阳所在位置为极点，轨道长轴方向为极轴方向，则行星的位置可用位矢r=r er表示[2]。

万有引力定律的建立是人类长期对行星运动的观察，科学记录观察数据（第谷的观察数据），并通过严格的数据分析、综合得到开普勒行星运动三大定律的基础上，牛顿借助运动定律，通过严格推理，地、月检验而得。借助万有引力发现的这个载体，挖掘其中的思维、思想，是对学生思维严密性培养的好素材。本文拟从3个高度不同的思维层面，还原物理学家在万有引力大小与距离平方成反比关系发现的思维过程，以期对学生思维品质的提升起到一定的促进作用。

开普勒在第谷几十年对行星观察数据的基础上，通过科学的方法总结得到了行星运动三大定律：

第一定律：所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上。

第二定律：对于任意一个行星来说，它与太阳的连线在相等的时间内扫过相等的面积。

如图1所示，Δt内行星和太阳的连线所扫过的面积ΔS=r·rΔθ=r2Δθ。

2 假设推理

根據开普勒行星运动第一定律，行星绕太阳做椭圆轨道运动，任何曲线运动都是变速运动，受力都不平衡，因而行星绕太阳运动时受力一定不平衡，必会受到周围天体对它的力的作用，在太阳系中可忽略其他行星的作用，认为其所受合力就是太阳对它的引力作用。并且，物体做曲线运动时在短时间内都可看成是在一小段圆弧上的圆周运动。假设行星所受太阳对它的引力与距离的n次方成正比，即设：F=krn。

行星运动到近日点和远日点时，由开普勒行星运动第二定律得：速度分别为最大值和最小值。因而，只有向心加速度，没有切向加速度，由向心力公式及牛顿第二定律得：

这种推理巧妙地利用假设法，抓住特殊位置进行推理，曲线运动在短时间内可以看作圆弧运动，进行了思维拓展，开阔学生的思维，享受到了思维大餐，但还是有一种小聪明和近似的感觉。

3 极坐标法进行严格推理

如图2所示，取太阳所在位置为极点，轨道长轴方向为极轴方向，则行星的位置可用位矢r=r er表示[2]。

由开普勒行星运动第三定律=k得：

即F=-4π2ker，太阳对行星作用力的大小与行星到太阳的距离成反比，方向沿两者连线指向太阳的方向，太阳对行星的作用力是吸引力。

通过严密的数理推理得到了引力的距离平方反比规律，学生虽然感觉数学上有点难，但基于对推理严密性的追求，还是能够接受的，再通过牛顿的地、月检验后，彻底接受了万有引力定律，并且还享受到了严密的逻辑推理过程，在震撼之余思维品质得到了提升，对学生的今后所从事的工作将会起到良好的促进作用。

参考文献：

[1]物理课程教材研究开发中心.普通高中课程标准实验教科书 物理2[M].北京：人民教育出版社，2010：37.

[2]周衍柏.理论力学教程（第二版）[M].北京：高等教育出版社，1986：14.（栏目编辑 罗琬华）