高考“数学史料题”的赏析与启示
2016-06-14陈雪莲王新宏
陈雪莲+王新宏
摘 要:每年高考试题中都有一定数量的“数学史料题”,它们背景新颖、内涵深刻、立意深远、意隽味浓,使数学的文化性、应用性和理论性有机结合,成为高考一道靓丽的风景线.它们不但丰富了高考命题的素材,也为当前课改引领了一个方向,更激发了莘莘学子的数学兴趣,培养了他们的数学创新能力,也为他们逐步形成正确的数学观与价值观提供了帮助.
关键词:高考;数学史;文化;意义;赏析
数学是人类文明的火车头,数学史是人类文化的重要组成部分.2003年颁布的《普通高中数学课程标准(实验)》在关于课程的基本理念中,明确指出要体现数学史的文化价值:数学课程应适当反映数学的历史、应用和发展趋势;数学对推动社会发展的作用;数学科学的思想体系;数学的美学价值;数学家的创新精神.
随着课程改革的不断深入,数学的人文价值更明显地凸显出来,已普遍受到重视.纵观最近几年全国各地的高考,出现了一些以数学史为载体的高考试题,成为新课改理念下高考改革和发展的一道靓丽风景.尤其是湖北省,已经连续多年命制此类考题,逐渐形成了湖北高考数学卷的一大特色和亮点.这一方面是为学生在平时学习时关注数学史提供导向,另一方面数学史作为一种数学文化走进高考,让高考试卷平添了几分文化色彩与气息;使高考试卷不再是“枯燥无味”“冰冷”的“人才考查”的一个工具,而是有趣有味的人文作品,读之赏心悦目,思之奥妙无穷,回味之意犹未尽.
一、试题扫描
查阅了近年来的高考数学试卷后发现:几乎每年都会出现与数学史相关的试题,涉及数学题材的内容极为丰富,如古老的“毕达哥拉斯数”“回文数”“阿波罗尼斯圆”“秦九韶算法”以及古籍文献中的立体几何的相关问题等(见表1).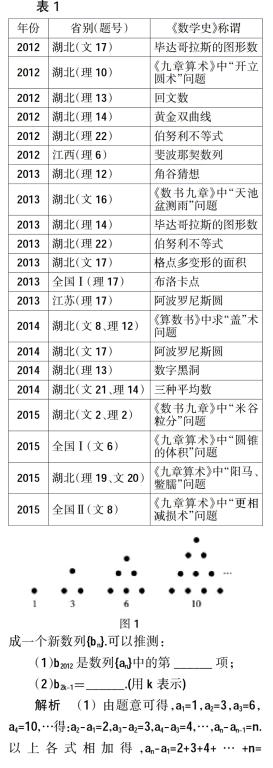

高考试卷的题型有选择、填空、解答及推演论证,以期通过运用数学史来考查学生的学习能力、逻辑推理能力、分析问题与解决问题的能力.
二、案例赏析
现遴选4个与数学史相关的高考题供赏析.
(一) 毕达哥拉斯图形数显风采
毕达哥拉斯是古希腊著名的哲学家与数学家,他所创建的毕达哥拉斯学派,是在众多的数学学派中对“形数”的研究最为突出的学派,该项研究强烈地反映了他们将数作为几何思维元素的精神,有效地印证了“凡物皆数”的观点.
例1 (2012年湖北文科第17题)传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图1所示的三角形数:
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}.可以推测:
(1)b2012是数列{an}中的第______项;
(2)b2k-1=______.(用k表示)
毕达哥拉斯学派中的数学家非常喜欢用形表示数,如:他们曾用图2形象地说明(1+2+…+n)2=13+23+…+n3.
(二)对称美回文数
“回文”是我国古典文学作品中的一种有趣的特殊体裁,有回文诗、回文联等.回文的特点是:在一篇作品中,作者精心挑选字词,巧妙地安排顺序,使得一篇作品倒过来从头读起,也同样是有意义的作品,如“云边月影沙边雁,水外天光山外树”,倒过来读,便是“树外山光天外水,雁边沙影月边云”,其意境和韵味读来真是一种享受!数学与文学有着相似之处,在数学中也有“回文数”,如121,2002,12321,回文仍是原数.在数学里,无论从左读到右还是从右读到左,都是同一个数的正整数称为回文数.
例2 (2012年湖北理科第13题)回文数是指从左到右读与从右到左读都一样的正整数.如22,121,3443,94249等.显然二位回文数有9个:11,22,33,…,99.三位回文数有90个:101,111,121,…,191,202,…,999.则:
(Ⅰ)4位回文数有 个;
(Ⅱ)2n+1(n∈N+)位回文数有 个.
解析 (Ⅰ)4位回文数只用排列前面两位数字,后面数字就可以确定,但是第一位不能为0,有9(1~9)种情况,第二位有10(0~9)种情况,所以4位回文数有9×10=90种.
(Ⅱ)法一:由上面多组数据研究发现,2n+1位回文数和2n+2位回文数的个数相同,所以可以算出2n+2位回文数的个数.2n+2位回文数只用看前n+1位的排列情况,第一位不能为0有9种情况,后面n项每项有10种情况,所以个数为9×10n.
法二:可以看出二位数有9个回文数,三位数90个回文数.计算四位数的回文数是可以看出在2位数的中间添加成对的“00,11,22,…,99”,因此四位数的回文数有90个,按此规律推导S2n=10S2n-2,而当奇数位时,可以看成在偶数位的最中间添加0~9这十个数,因此S2n=10S2n,则答案为9×10n.
回文数体现了数学背景下的对称之美,回文数有趣而美妙的性质有:
(1)除了11,1331以外,所有回文数的位数都是奇数.
(2)在完全平方数、完全立方数中的回文数,其比例要比一般自然数中回文数所占的比例大得多;例如112=121,222=484,73=343,113=1331,都是回文数.
(3)人们至今未能找到四次方、五次方以及更高次幂的回文素数;于是数学家们猜想:不存在nk(k≥4,k,n∈N*)形式的回文数.
(三)魅力阿波罗尼斯圆
一般地,平面内到两定点的距离之比为常数λ(0<λ≠1) 的动点的轨迹是圆,这个圆叫作阿波罗尼斯圆;阿波罗尼斯是继欧几里得、阿基米德之后的又一代著名数学家,他们三个并称为亚历山大时期的数学三巨匠.以阿波罗尼斯圆为背景的高考试题屡见不鲜,据统计,在近十年高考中,出了13道考题,阿波罗尼斯圆的魅力体现得淋漓尽致.
解析3(特殊点)
既然对圆O上任意一点M,都有|MB|=λ|MA|,使得λ与b为常数,那么我们何不把点M取为特殊点呢?取M(1,0)与M(0,1)代入|MB|=λ|MA|得:b2+1=5λ2,(b-1)2=9λ2,得b=-,λ=.
点评 大部分考生想不到特殊化的数学思想解题,主要原因是他对特殊与一般的数学思想理解得不够深刻,不够到位,再加上平时训练得又较少甚至没有,故想不到简便的解题策略.
高考源于教材,高于教材,阿波罗尼斯圆的身影就在我们的教材中:(人教A版必修2习题4.1 B组第3题)已知点M(x,y)与两个定点O(0,0),A(3,0)的距离之比,求点M的轨迹方程.
(四)古色古香中国古文献
据不完全统计,几乎每一年都有以我国古代数学名著如《九章算术》《数术九章》《算数书》等为素材命制的中国古文化高考真题.它们大多与体积有关,以古代社会人们的生活实际和生产实际为背景(对考生来说比较陌生与新颖),并且是用古汉语描述的.这就要求考生懂一定量的古汉语知识,能从试题的字里行间挖掘出数学要素,不断地经历直观感知,观察分析,归纳类比,空间想象,抽象概括,数据处理,运算求解.反思与建构等思维过程,这一方面,引导考生对题目中所蕴含的数学知识、方法进行提取、推理、思考、判断是考生解决问题能力的体现,但另一方面我们也不得不惊叹古人的聪明、睿智以及对数学问题用古汉语诗意般的精彩论述.
例4 (2013年湖北文科第16题)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸. 若盆中积水深九寸,则平地降雨量是 寸.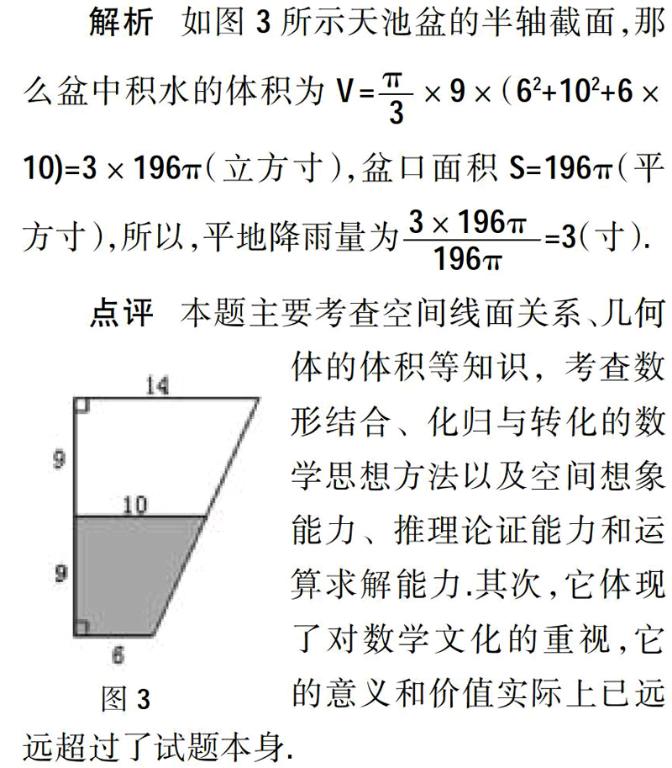
解析 如图3所示天池盆的半轴截面,那么盆中积水的体积为V=×9×(62+102+6×10)=3×196π(立方寸),盆口面积S=196π(平方寸),所以,平地降雨量为=3(寸).
点评 本题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法以及空间想象能力、推理论证能力和运算求解能力.其次,它体现了对数学文化的重视,它的意义和价值实际上已远远超过了试题本身.
从以上可以看出,关注数学史、数学文化以及数学科普知识,对我们有着一定的导向作用,教育功能,以及非常重要的现实意义;它们在一定程度上展示了原本数学的美,传达了一种勇于探索、锲而不舍的数学精神.因此,高考对数学史与数学文化的母子、亲情关系另眼相看,它们也一定会引领我们的日常教学,创建富有数学文化魅力的灵动课堂,让学生陶醉在数学史的历史长河中,享受在数学文化对人类文明的贡献中,真切体会数学的美、数学的精神、数学的伟大所在.
三、启示
(一)体现稳定与创新并举
高考数学一直在贯彻坚持稳定为主,注重基础考查,突出能力立意,着力内容创新,不一味迎合中学数学教学模式.因此,从实际出发,结合学生的实际与考试效度的需要,兼顾公平性与创新性,选择恰当的带有人文性的“数学史料题”便顺理成章了.
(二)为教学改革铺砖垫瓦
高考中的数学史料题,素材新颖、构思精巧、立意高远、意隽味浓、视角独特、导向鲜明等特点都充分体现了新课改的理念.
高考试题中蕴含数学史料题的深意,绝不单纯是“秀”几道高考题这么简单.中学教师应加强数学史对数学课改的影响,为此教学中应该重视数学史的教学与反思.运用历史发生教学原理,不仅可以启发学生思维,帮助学生掌握学科体系,而且可以激发学生的学习兴趣,培养学生的探究能力;因此在开展数学教学时,应当适当了解历史上相关问题的发展过程,分析哪些困难可以通过数学史的途径加以克服,然后再根据学生的需要设计教学,这样做,可使数学史的应用深入到学生的认知层面,有利于培养学生的数学思维能力和数学问题意识.
可以预见,数学史是一座有待开发的宝山,有待于我们从多角度、多方位进一步开发,进而引导高中数学教学和评价方式的改变,为教学改革铺砖垫瓦.
(三)增强了数学的育人功能
数学教育是数学文化的教育,而数学史是数学文化的重要载体,通过对数学家发现问题、发明方法、创造思想的了解,可以激发学生学习数学的兴趣,从而培养学生的创造精神和创新能力;另一方面,数学科学的思想体系、数学的美学价值、数学家的创新精神、数学在人类文明发展中的作用,都将有利于学生逐步认识真实的数学以及形成正确的数学观和价值观.
