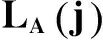具有词汇结构的复杂agent网络语言竞争模型

王　超，毕贵红，张寿明，于群修

(1.昆明理工大学信息a.工程与自动化学院，b.昆明理工大学电力工程学院，昆明 650500;2.国家知识产权局专利局专利审查协作天津中心，天津 300280)



具有词汇结构的复杂agent网络语言竞争模型

王超1,2，毕贵红1b，张寿明1a，于群修1a

(1.昆明理工大学信息a.工程与自动化学院，b.昆明理工大学电力工程学院，昆明 650500;2.国家知识产权局专利局专利审查协作天津中心，天津 300280)

摘要:利用agent社会圈子网络理论构建语言竞争网络，利用两个F长度的二进制位串表示可能的双语内部结构，在此基础上给出一种新的动态微观语言竞争模型。分析了语言地位、网络结构、语言遗传率和语言学习率对网络中agent所掌握的词汇量、语言类型及熟练度演化的影响。模型反映了不同语言者之间通过交流和竞争实现语言内部结构演化涌现宏观语言态势的机制。仿真结果表明，模型克服了其他模型不能反映系统中语言使用机会和频次对语言竞争的影响。

关键词：agent；社会圈子；动态网络；语言内部结构；语言竞争

0引言

在全球范围来看，已经有超过750种语言灭绝，还有许多语言也只有少数的使用者[1]。联合国估计，目前世界上现存语言中，有一半的语言只有不到一万名使用者，四分之一的语言只有不到一千名使用者，并且，除非采取有效措施，否则在一个世纪之内这些语言(至少3 000种)都要消亡[2]。语言濒危的原因非常复杂，包括地理环境、人口分布与扩散、语言政策、语言地位和语言态度、语言环境和语言内部结构等因素及其相互作用，而且这些因素是随时空变化的，呈现异质性。拯救濒危语言，有必要对语言传播、竞争和调控的机理和动力学特性深入研究，以揭示语言衰退、消亡和共存的原因，进而寻求濒危语言保护和干预措施。

国际上语言竞争与演化动力学研究主要利用系统动力学方法、复杂系统建模和仿真方法。语言作为一个复杂适应性系统体现在以下几个方面[3]：1)系统由相互作用的个体(语言社区中的说话者)组成。2)系统是自适应的。说话者的行为建立在其过去的交互过程，而且当前和过去的交互过程一起前馈给将来的行为。3)说话者的行为是从感受机制到社会动机等一系列因素相互竞争的结果。4)语言结构从相互影响的经验模式、社会交互和认识过程中涌现出来。另外，语言的交流传播过程的互动性，决定了人与人之间的接触网络是语言交流传播发生的基础。所以，语言交流传播系统是个复杂的社会系统，可以用复杂适应性系统理论及其建模方法、复杂网络及其建模方法以及两者结合的方法来研究语言竞争模型及其动力学性质。

Abrams等[4]利用微分方程来描述社会中两种语言竞争引起的语言使用模式的变化情况。Mira等[5]在Abrams中加入双语者，两种竞争语言之间的迁移通过双语过渡。Minett等[6]在引入双语者的前提下，为语言之间的转换设定了同代水平语言传播和隔代垂直语言传播两种模型，更合理地解释语言在人群中的传播过程。Kandler等[7]融合双语者、垂直和水平语言传播、社会结构和人口因素给出了一个综合性的Abrams扩展模型，并考虑语言保护政策对语言保护的作用。上述对Abrams模型的扩展工作是为了验证人口学、语言和社会因素对语言竞争和消亡的重要作用，是一种基于微分方程的语言竞争动力学模型，属于宏观模型。2013年张梦翰和龚涛在《PNAS》上发表的文章是该领域近年来取得的突破性成果[8]。在Lotka-Volterra[9]演化生物学竞争模型的基础上给出了新的语言竞争模型，模型中定义了两个具体的参数，即语言竞争的影响率和传承率，并给出了一个语言传播规则和两个语言传承规则，基于给定的规则利用相关语言和人口调查数据计算模型中的两个参数。改变了之前模型参数过于抽象无法具体计算的问题，而该模型中的参数具有社会和语言学的具体含义，可以显式计算，其中的数据可以从人口普查数据和地理信息系统中获得。作者解决了语言竞争模型参数可估算的问题，并用实例验证了该理论和模型的可行性、可靠性和可用性价值。该文章取得的研究成果为语言竞争模型与实际社会文化相结合的方法指明了方向。

复杂agent网络建模方法近年来得到越来越多的重视。Stauffer等[10]给出了AS模型的微观仿真模型，分析了系统社会连接网络和一个d-维网络上的系统演化特征。Castelló[11]扩展了Stauffer的模型，模型引入了双语者和社会网络，除了使用d-维网络外，作者还考虑了能够同时实现短距离和长距离交流的小世界网络。网络上的agent每一个时间步由一种语言类型转化为另一种语言类型的概率由与之相连的网络邻域中各种语言类型agent的比例来确定。研究表明无论是双语者或者是社会结构都不能产生社会地位相同的两种语言共存。双语政策不是保护濒危语言的稳定策略，双语agent经常存在于两个单语者的空间交界处，从而有利于两个群体的交流，小世界网络的社会结构则加速了语言的濒危过程。Minett和Wang[6]为了研究具体政策干预机制和初始条件下语言竞争系统的一系列可能行为结果，在他们给出的微分方程基础上建立了微观agent仿真模型。模型包括了两种单语者和一种双语者agent类型。agent的语言可代间垂直传承，也可以代内水平传播。在每一个时间步agent采集网络上的邻域信息来确定语言转用的概率。作者分析了全连接网络和局域世界网络上[12]的语言竞争动态特性。研究结果表明了政策调控机理的复杂性，首先社区越能有效提升濒危语言的社会地位，接下来的调整政策就可以推迟执行；其次，在没有政策干预情况下，社会结构不影响语言竞争的动态特性，然而政策调控在全连接的网络中更容易取得成果，这也意味着在实际的社会网络中政策调控更加困难。

目前复杂agent网络模型综合考虑了语言的社会结构、人口密度、语言地位以及双语因素对语言共存的影响，在语言竞争动力学研究中取得了重要进展，但是目前还存在如下问题：1)网络以静态网络为主，未考虑社会网络的动态特性。开始，人们采用计算机生成在某些方面符合真实社会接触网络特征的理想网络，如小世界网络、无标度网络等，通过研究这些理想网络中的语言交流传播过程来间接了解语言交流传播与真实社会接触网络结构特征之间的关系[11]。进一步，研究者们考虑了具有社群结构的更为实际的社会网络结构对语言传播的影响。如具有局域世界模型[6]和具有社区结构的网络模型等[13-14]。现有的复杂网络语言交流模型主要关注的是网络的拓扑结构特征，如小世界特征、无标度特性、高聚类特征和网络的社群结构等对语言交流传播的影响，而对网络结构随时间的变化关注甚少，也就是说，这些研究基本上都是以静态网络为基础的。而真实的社会接触网络由于受到人员在区域内或区域间的流动使得网络拓扑结构特征发生变化，从而影响到其上的语言交流传播过程。2)语言交流竞争网络中某个节点语言使用类型的迁移概率由该节点邻域的某种语言人数的比例、语言地位等来确定，语言没有内部结构(如词汇量)，没能考虑语言学习和掌握程度的动态变化过程，不能反映系统中语言使用机会和频次对语言使用类型及其能力变化的影响。

著名社会仿真学者Gilbert和Hamill[15]提出了一种基于agent的社会圈子网络理论来构建具有多种实际社会网络统计特征的社会网络生成方法，它是一种基于微观个体行为生成社会网络的方法，网络的生成和演化由agent来管理，更加接近实际社会的运行机制，可以灵活描述大规模社会网络时空耦合演化的机理。本文引入基于agent的社会圈子网络模型来研究个体行为和个体之间的语言传播构成的社会网络复杂agent网络模型，该模型能很好地体现语言网络中的特点：1)社会圈子网络中的个体网络参数和整体网络参数都更接近实际，个体网络参数具有异质性、度胖尾分布、高聚类系数，且随时间变化；整体网络参数具有低密度、度度相关性、社群结构以及短路径等特点。2)通过为个体设置不同的社会半径可以改变社会圈子的大小，而社会半径大的个体有可能连接到其他小团体，形成圈子之间的弱连接，并且社会半径大的个体倾向于互相连接，可以表达人们社会交往圈子和社会网络复杂的社群和层次结构的异质性。3)agent可以断开原来的社会圈子里的关系，移动到不同的位置在社会圈子内重新构建新的社会网络，可以描述具有流动性的社会网络。Kosmidis[16]提出基于agent建模方法来研究两种语言竞争问题。模型中每个agent都是潜在的双语者，每种语言最多拥有10个词汇，用一个长度为10的二进制位串来表示。agent可以从另一个agent中学习词汇，也可以忘记词汇。假设agent的适应度值(定义为agent的繁殖能力)随着从其它agent学到的词汇量增加而增加。作者探讨了不同的初始适应度值如何导致不同语言词汇量的变化以及人口动力学特征如何导致一种人群长久的语言优势。研究结果表明：持不同语言的人群的空间分布，能使系统表现出语言人群区域模式的形成或分隔。初始适应度优势能导致良好的空间分布，加强了该种群人口的生存能力。多种情况下，系统能到达两种语言共存的最终状态。然而，如果是一种人群的人数和适应度值都远大于另一种人群，则只有一种语言以比其初始词汇量稍微丰富的词汇存在下来，所以作者认为出现了同义词现象。Schwammle[17]研究了考虑人口生育的语言竞争模型，模型中的agent位于规则网格上，能够说两种语言中的一种或两种。如果父母都说同一种语言，则其子女学习同一种语言。如果父母能说不同的语言，则其子女以一定的概率po学习双语，否则以相同的概率学习其中一种语言，同时agent能按pf概率忘记已学会的语言。双语者通过统计自己邻域内说第1种语言或第2种语言的人数，并以概率pf忘记邻域内人数少的那一种语言。研究了初始说不同语言的两个区域界面的稳定性及其结构的定量分析。研究结果表明不同的语言不能共存很长时间，如果它们不是地理分割的，双语者相对于单语者的比例随年龄增长按指数方式减少。以上研究提示我们复杂agent网络模型也可以用相同的方法来表达单语和双语agent的语言内部结构、掌握程度和学习使用过程。通过对语言使用者个体在具体语言环境中的语言使用学习行为和内部语言结构的演化及其相互作用的机理建模来设计更为丰富的agent，从而提高语言竞争社会仿真系统的真实性和深刻性。

本文利用基于agent的社会圈子网络理论构建语言竞争网络并引入agent的词汇结构的基础上给出一种新的动态微观语言竞争模型。本模型主要特点表现在：1)基于社会圈子理论构建的社会网络不仅结构上更加接近实际，而且网络中agent个体的出生死亡、短途移动及长距离移动可以引起网络的断开和重连，网络具有动态特性。2)个体agent利用两个长度为F的二进制位串表示其可能掌握的双语内部结构，可以体现agent掌握的语言类型、词汇量及其熟练度的变化过程，以此反映不同语言者之间通过交流和竞争实现语言内部结构演化的微观现象。3)网络上具有不同语言地位的agent之间通过交流实现词汇的学习和遗忘，并推动语言在网络上的水平传播，词汇的学习和遗忘模型考虑了语言地位和语言交流机会的影响。4)网络上的agent可以通过父辈遗传词汇给子代实现语言的垂直传播(单语或双语)。

1语言竞争的两种微观模拟模型

1.1Kosmidis微观语言竞争模型

Kosmidis等[16]提出一种基于内部语言结构的建模方法—蒙特卡洛方法来研究两种语言竞争问题。模型中包含单语A、单语B和双语AB三类语言；每个agent最多拥有20个词汇，用一个长度为20的二进制位串(VA和VB)来表示，位串中的数字1表示已知单词，数字0表示未知单词，A语言和B语言的语言结构如式(1)和(2)所示。

(1)

(2)

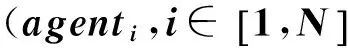
1)语言的水平传播。网络中，agenti与局域摩尔邻居(距离该个体最近的8个方向相邻个体)agentj进行交流。交流成功，agenti以概率p从agentj学习词汇；交流失败，以概率q忘记词汇。

2)agent繁殖。agenti的繁殖率由自身的适应度值fi来确定。模型中的适应度值fi随着从其它agent学到的词汇量增加而增加，由适应度值确定agent的繁殖率pi，agent的繁殖根据两种公式，全局模型pi=fi/∑fi，其中∑fi为所有个体适应度的总和，全局模型反映个体的信息来自于社会；局域模型pi=fi/∑fi，∑fi为局域摩尔邻居的总和，局域模型反映其信息只依赖于局部邻居。

3)语言的垂直传播。当agenti满足繁殖条件，父辈agenti在空的摩尔区域(距离该个体最近的8方向相邻区域)繁殖个体，子代agentj完全继承父辈的词汇结构。

该模型模拟了语言的代内水平传播，即同辈之间语言的学习与遗忘过程，同时利用适应度模型模拟个体的繁殖能力并利用垂直传播模型模拟语言从父辈遗传语言给子代的过程。

1.2Castelló复杂agent社会网络模型

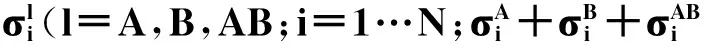
(3)

(4)

公式(3)给出agent从一种单语(A或B)变成双语AB的概率；公式(4)反映agent从双语到单语的转换概率。转换概率pi与其竞争语言邻居的密度成正比。公式中sA和sB表示单语A和单语B的语言地位，在一个拥有两种语言的社会中，语言的社会地位之和为1，即sA+sB=1，Castelló模型中假设sA=sB=1/2；公式同时表明，两种单语需要通过双语AB过渡。语言之间的转换概率由语言地位和邻域中某种语言的人口密度共同决定。该模型研究在理想社会网络结构(小世界网络)下，不同语言地位和不同人口密度对语言竞争的影响。模型综合考虑了语言的社会结构、人口密度、语言地位以及双语因素对语言共存的影响。

1.3具有语言内部结构的复杂agent网络语言竞争模型

Kosmidis模型[16]将宏观的语言竞争现象微观化，微观个体词汇的学习与遗忘可以描述人与人之间通过词汇交流实现语言传播的微观过程，但是语言交流网络属于一种社会接触网络，需要考虑社会结构对语言传播的影响，所以Castelló模型[11]中所加入的静态社会接触网络(小世界网络)，分析其对语言竞争影响；双语者的引入解决了Abrams-Strogatz模型[4]中两种单语直接相互转化的偏离实际的问题；更进一步，语言社会地位为个体间语言的学习和遗忘提供了更实际且具象的解释，语言地位较高的语言，该语言被学习的几率较高并且更难遗忘，反之亦然。

结合两种模型，本文利用社会圈子理论建立社会接触网络，网络中的个体通过社会半径建立连接，不同社会半径大小的个体构成不同的社群结构，网络中的所有个体可以断开旧连接移动到不同区域建立新连接，描述社会网络的动态流动性，弥补了小世界网络的静态缺陷；在此基础上引入微观语言竞争模型和双语因素，语言内部的微观词汇可以将抽象的宏观语言细化。在语言词汇的交流过程中引入语言的社会地位，合理解释现实社会中词汇学习和遗忘的原因，同时语言社会结构的不同对语言竞争也有一定影响。

2基于agent社会圈子理论的语言传播竞争网络模型

Li和Chen推广BA无标度网络提出局域世界模型思想。网络中，个体优先考虑局部区域内的个体之间的连接(合作)，其次再考虑区域之间的连接(合作)，反映到现实中许多国家都致力于加强与各自区域内其他国家的经济和贸易往来，模型中的度分布介于指数分布与幂律分布之间[12]，模型网络属于静态网络。

著名仿真学者Hamill等[15]提出一种基于agent的社会圈子网络理论来构建具有多种实际社会网络统计特征的社会网络生成方法。网络中，个体的网络规模由社会半径的不同而产生差异同时规模随时间动态变化；网络中的社群人口密度较低、具有度度正相关性、可以形成社群结构并具有平均路径短的特性，网络中的度分布服从长尾的泊松分布，如图2b所示。agent可以自己构建和管理社会关系，灵活描述社会动态演化的机理。微观语言竞争传播网络属于一种典型的社会网络，社会圈子网络可以较完整地反映实际社会中语言竞争的特点，所以，社会圈子网络可以用来研究微观语言竞争网络模型。

社会网络模型可以被看作是一张社会地图，显示了人在网络中的分布与联结。网络中，个体拥有长度不等的社会交流半径，以个体自身为中心，社会半径长度为半径作圆形成个体的社会圈子，社会圈子大小的不同使个体交流范围产生差异。当两个体中心点的连线的长度Q小于等于连线两端个体较小社会半径r时，个体建立连接产生联系，图1a中Q>r，所以不产生联系；图1b中Q

图2a中“×”节点的社会半径长度为20，“●”节点的社会半径长度为30，“▲”节点的社会半径长度为40。度分布、聚类系数以及度度相关系数是反映社会网络结构的主要参数。图2b中，不同社会半径的个体度分布呈泊松分布，而且社会半径小的个体人数最多，半径越大人数越少，这与现实社会中大多数人的联系范围较窄而少部分人联系范围广泛相一致；图2c表示网络有较高聚类性(≈0.6)，节点的聚类系数在0.2到0.9之间，平均0.574，所以网络中大部分节点满足朋友的朋友也是朋友的连接关系；计算出网络的皮尔逊度度相关性系数为0.435，网络正相关，表示同类相聚。这些参数都表明构建的网络满足社会网络的主要特征。

社会圈子网络还可以实现网络的动态特性，通过引入短距离移动(日常短途移动)和长距离移动(长途旅行等)来模拟人口的流动，人口流动会引起社会网络结构的变化。规定短距离移动为个体在一个时间步长内移动一个单位长度的距离，移动距离短，所以人口的移动可能不会改变个体网络以及整体网络结构；规定长距离移动代表个体在一个时间步长内移动大于自身社会半径的距离，移动距离长，所以个体网络以及整体网络结构都将发生改变。如图3a所示，当agentj移动到A，agenti的个体网络结构改变；当agentj移动到B，由于仍在agenti的联系范围内，所以agenti个体网络结构不变。图3b中，agenti从A移动到B，移动距离L超过自身社会半径r，所以agenti的个体以及整体网络结构改变。

3语言传播模型

3.1agent语言结构

语言接触竞争会影响语言结构的各个方面，语言结构包括语音、词汇和语法等方面。语言能力的高低，可以从词汇量多少、语法结构的完整性和复杂程度以及类型差别以及听说读写基本语言的强弱等方面进行分析，但词汇最能反映一个人的语言能力[18]，语言学家经常使用核心词汇表对被测试人员进行语言能力测试和熟练度分级。所以语言接触竞争模型应该以接触网络中语言个体间的词汇获得与变化过程为核心。

二进制位串中词汇的掌握情况反映个体的语言类型。语言类型规定：1)LA(j)中至少有一位为1而LB(j)中全为0时，规定为单语者A；2)LA(j)中全为0而LB(j)中至少有一位为1时，规定为单语者B；3)LA(j)和LB(j)中都至少有一位为1时，规定为单语者B，如图4a～图4c所示，对应公式(5)～(7)。

(5)

(6)

(7)

3.2agent词汇的水平传播规则

社会语言网络中，不同语言者通过接触交流来学习语言，以丰富自己的词汇量，同时在交流过程中，也会伴随着词汇的遗忘。现实中，语言的语言地位相异，优势语言的语言地位普遍较高且人口基数较大，弱势语言地位较低且人口基数少。个体进行词汇学习与遗忘的可能性也会随着语言地位的不同呈现不同的态势。

人与人通过交流来表达个体思考的过程，语言的水平传播模型可以反映这一过程。模型中，个体进行词汇学习和遗忘需要满足条件C：1)个体之间具有图2a中的边连接关系(二者有联系)；2)在1)的前提下满足交流概率(pcommunication)选择对应个体进行词汇的学习和遗忘。

A语言词汇学习遗忘公式：

(8)

(9)

B语言词汇学习遗忘公式：

(10)

(11)

3.3语言熟练度因子的计算

语言交流成功后，词汇的掌握情况有所改变，语言熟练度能够反映语言的热门程度以及交流使用的频次。交流后，两个有联系的个体对应位置的词汇由之前掌握情况的不同变成同时已知该词汇，语言A的熟练度(fA)增加1，语言B的熟练度(fB)同A。如图7所示，agenti中A语言未知的第2个词汇由于学习了agentj中对应的已知词汇而掌握了该词汇，此时，两个体对应位置的词汇全部为已知状态，则A语言熟练度加1，即fA+1。

3.4agent词汇的垂直传播规则

人口的出生或死亡能够反映人口数量的动态变化，而个体的繁殖又需要考虑语言的遗传和继承。模型设置出生率(pb)以及死亡率(pd)反映这一特征，网络中的个体以pb的概率繁殖新个体，以pd的概率死亡。同辈单语者通过学习可以变成双语者，当个体满足pb后，父辈双语者以一定的几率(双语遗传概率，Pbilingual)将双语遗传给子代个体，个体的词汇遗传流程图如图8所示。图中，父辈双语者满足双语遗传概率，将双语遗传给子代，子代为双语者AB；否则，如果满足单语A的遗传概率，子代为单语者A，不满足则为单语者B。

4语言竞争agent网络演化模拟模型

1)建立agent并初始化两种单语人口：创建N个agents并随机分布在200×200范围内的二维空间网络内，分配单语者A和单语者B的人口比例(xA和xB)，两种人口比例之和为1，即xA+xB=1。

2)agents属性设置：设置两种语言的语言地位，优势语言的语言地位为sA，弱势语言的语言地位为sB，sA>sB；为个体分配社会半径并设置小、中和大3种社会半径的人口分布比例(ys、ym和yb)，3种人口比例之和为1，即ys+ym+yb=1。建立社会圈子网络。

4)生成社会网络：agents根据自身拥有的社会半径属性，利用社会圈子原理建立社会网络，如图3所示。

5)网络的人口流动：在生成的社会网络中，引入两种移动方式，短距离移动和长距离移动。设置短距离移动和长距离移动人口比例(xDM和xLM)

6)更新个体之间的连接关系：当个体间连接的长度同时大于链两端的个体的社会半径时，连接断开，否则保持连接。

7)判断死亡/出生人口及语言继承：死亡人口：遍历网络中的个体，当满足死亡概率(pd)时个体死亡；出生人口：遍历网络中的个体，当满足出生概率(pb)时繁殖后代；语言的遗传和继承：agent利用词汇垂直传播规则从父辈遗传和继承词汇，父辈个体满足繁殖条件后，进行语言的遗传，当父辈双语个体满足双语遗传概率(pbilingual)，子代继承父辈的双语特性；否则为单语者之一。

8)重构社会语言网络：经过移动、人口的出生以及死亡后，重新建立社会网络。

9)个体的语言交流：个体的语言交流首先满足个体在其社交范围内，其次满足交流概率(pcommunication)才能进行语言的交流。当满足上述条件后，个体进行语言内部的词汇交流，设定p为学习率，q为遗忘率，学习词汇的概率与语言地位成正比，遗忘词汇概率与语言地位成反比，具体如式(8)～(11)。

11)网络的动态更新：随着时间更新，重复执行步骤5)～10)。

5仿真结果分析

Castelló模型在小世界网络中利用个体周围的语言人口密度和语言地位决定语言之间的转换[11]，而Kosmidis模型在二维规则网络中利用微观个体的学习和遗忘反映语言传播的微观过程[16]；本模型在语言竞争网络中利用个体内部词汇交流的微观过程反映宏观语言变化情况：将社会圈子网络作为语言竞争传播网络，通过设定个体之间词汇交流的机会实现词汇的学习和遗忘，体现词汇的变化，进而反映语言种类的变化。模型以NetLogo[19]为平台，模型中的部分参数的初始值借鉴了Kosmidis提出的模型中的参数[16]。参数设置如表1所示。仿真试验所有结果均是在相同模型参数条件下重复30次仿真试验取平均值得到的结果。

5.1语言地位对人口比例以及词汇的影响

实际生活中，随着社会开放性的提升，不同地区语言的同一化现象明显，语言地位较高的强势语言被大部分人口认同并使用，而语言地位较低的弱势语言由于语言竞争力相对较弱，所以使用人口较少，同时有衰减的趋势。通过改变语言地位模拟混居社会下不同语言地位对语言竞争的影响。图9仿真实验中，模拟单语A的语言地位分别为0.7、0.55和0.3三种情况对语言竞争的影响。

图9中，从图a至c随着A语言地位降低以及时间的推移，A语言的人口比例趋势也在不断变化。如图9a所示，A语言地位(sA)为0.7时，强势单语A的人口比例在250步左右占据全部人口，而弱势单语B和双语逐渐消亡；如图9b所示，随着A语言地位的下降(sA=0.55)，单语A的人口比例增长趋势逐渐放缓，双语以及弱势单语B保存时间延长；如图9c所示，当sA=0.3，语言A和语言B的强弱关系发生转换，语言B变成强势语言，随着时间推移，A语言和双语逐渐消亡，而单语B占据全部人口。所以，语言地位的提升促使弱势语言人口更主动学习和继承母语，在兼用强势语言同时减少语言转用保证在人口总基数不变的前提下，增加弱势语言保持人口和保持时间。同时，模型中语言人口比例相比语言地位来说是较被动保守的参数，语言地位才是关键的主动积极参数。

个体语言内部微观词汇结构的演化结果导致宏观语言的涌现。图10的模拟结果中，A语言地位(sA)为0.7时，强势单语A的整个人群的人均词汇量逐渐增加，在500步左右达到最大词汇量10；初期A语言人群通过接触也掌握少量的B语言词汇，但随着整体人群中掌握语言B词汇数量的快速减少，A语言人群中掌握的少量B词汇量只保持了100多步；相应的在B语言人群中，随着兼用A语言的双语人群和转用A的单语人群的增加，B语言人群中人均掌握得B词汇量快速减少，200步以后B词汇从B人群和A人群中消亡，B人群全部转用A语言。当A语言地位(sA)为0.55时，B语言的语言地位提高为0.4，随着B语言竞争能力提高，A语言人群中掌握B语言的词汇量逐渐增加，在500步左右稳定在人均B词汇量5左右，而A语言人群受此影响，人均最大A词汇量稳定在8左右，相对于前一种情况有所减少；相应的在B语言人群中，A语言的词汇量增加较快，在100左右之后，B语言人群兼用的A词汇量与A语言人群相当，并同步增加，最后在500步左右稳定在8左右，而B语言人群掌握的B词汇量由于竞争的原因词汇量初期有一定减少，但100步后逐渐增加，500步后达到5左右，从中可以看出随着B语言地位的提高，其竞争能力得到提高，B词汇在A语言人群和B语言人群都得到了一定的保存。当A语言地位(sA)降为0.3时，B语言的语言地位提高到0.7，A语言和B语言人群人口比例保持不变的情况下，A语言与B语言的地位发生了逆转，A和B词汇量在网络中的传播方式与第1种情况发生相反的变换，B词汇量得到保持，A词汇最终从网络中消失。综上所述，随着B语言的语言地位的逐渐提高，B词汇量在网络中存留时间和数量都得到增加，直到网络中B语言词汇占绝对优势。图11a中单语A的语言地位大于单语B，A语言词汇在网络中成功交流频次高于B语言词汇，所以网络中语言A熟练度的平均值比语言B高；降低语言A的语言地位，语言B的熟练度有一定提高，由于语言A基数较大的关系，在社会大整体下的语言A熟练度仍然较高。语言地位的改变会影响该语言在社会中应用的比重，影响社会群体对语言词汇的接受程度，从而影响掌握词汇的数量。实际中，虽然某种语言的初始人口比例较小，但是随着语言地位的提升，会影响语言在政治、经济和文化方面的地位，增强语言的社会影响力，提高社会人口学习使用该语言的主动性，促进语言学习的自觉性，促使人们学习语言从不自觉到自觉，从而改变该语言的未来的趋势。

该实验的图9实现了Castelló模型[11]中单语A人口比例高于单语B人口比例，单语A与单语B语言地位变化时网络中单语A、B和双语AB人口比例的宏观演化趋势；图10实现了Kosmidis模型[16]在单语A人口集中度高于单语B人口集中度，单语A和单语B的语言适应度值变化的情形下不同类型人员平均词汇量的演化关系。模型调整语言地位后仿真结果能同时反映Kosmidis以及Castelló的主要仿真结果，验证了复杂语言词汇内部结构能够反映外部宏观语言的变化趋势。进一步通过调整社会交往半径、双语遗传率以及语言学习率等调控措施来分析系统的演化规律。

5.2社会半径对人口比例以及词汇的影响

随着社会的发展，科技的进步，交通和通信技术的不断发展使得人们之间的时空隔绝越来越被淡化，人们交流的空间范围被无限放大。图12中，个体的小社会半径(Sr)、中社会半径(Mr)和大社会半径(Br)分别由15、25和35增加到30，50和70，半径扩大为原来的两倍。当社会半径较小时，个体可联系范围较小，3类语言的共存时间为250步；随着社会半径的增加，社会圈子不断增大，个体间的交流会不断增加，语言竞争加剧，3类语言的共存时间缩减为150。社会发展扩展了交际范围，从而加剧了语言之间的碰撞，强势语言占据人口以及社会地位的优势获得了多数人的支持，而弱势语言本就处于劣势，在与强势语言的碰撞当中显现疲态，逐渐消亡。

社会半径的改变也会影响语言内部的词汇数量。图13中，社会半径较小的弱势单语B的词汇数量在200步变为0，而社会半径较大的弱势单语B在150步即变为0；伴随社会半径增大后社交范围的增加，强势单语A的掌握速率和效率也随之提高，图13b中的单语A词汇在350步时达到最大值，交流范围的扩张使得语言词汇的交流更加频繁，强势语言词汇使用的强度加大，而弱势语言词汇逐渐被淡忘，导致最终弱势语言更快消亡。图14b在增加整体社会半径后，两种单语的交流频次和成功次数显著上升，反映了扩大人口之间的社交范围可以增加语言的使用频次和使用热门程度。交流范围的扩展，使得人们不得不通过学习新语言进行沟通，人们必须主动学习新语言才能完成所需任务，这样增加了强势语言传播的能力，同时提高了弱势语言保持的难度，但现实条件下人们不可能通过限制人们交流范围来提高弱势语言的保护强度，所以政府要出台相应政策来保护弱势语言。

5.3双语遗传概率对人口比例以及词汇的影响

双语的遗传主要表示双语者父母在家庭中语言环境中主动传承双语给下一代的行为，这样可以减少下一代在双语家庭中直接转用强势语言的可能性，主动增加语言的自我竞争能力以及生存能力。图15仿真过程中，双语遗传概率由初始的30%增大到90%，图中3种语言人口的趋势走向变化明显：初始3种语言的趋势为强势单语A获得所有人的支持与学习，而双语AB与弱势单语B最终走向消亡；提高双语遗传概率后，3类语言趋于平衡共存状态。双语遗传比例的增加促进了弱势语言通过双语的方式保留下来，同时控制两种单语平衡共存的走势。

由图16a可知双语遗传率较小时，语言地位高的优势语言在300步时已经被所有人接受，弱势语言消亡，只有极少双语存留；随着双语遗传率的增加，双语化社会的趋势愈发明显，图中大部分个体同时掌握两种单语，还有一部分以两种单语形式保留。图16b～e可知，社会圈子网络的在300步变化后，度分布仍然服从泊松分布且节点的平均聚类系数较大(≈0.6)，符合社会网络的主要特征。

从微观词汇的掌握情况再次验证了提高双语遗传概率可以使不同语言地位的语言达到一个稳态共存状态。图17a双语遗传率为30%，弱势单语B的词汇数量最终变为0；图17b在提高双语遗传率后弱势单语B的词汇量有所提升，两种语言的词汇数量稳定增长，两种语言的词汇数量均不为0。图18b在增加双语遗传率后，两种单语的熟练度有了一定的提升，说明语言在社会中交流比重增加，使用的频次亦增加。因此，在日趋激烈的政治、经济和文化的竞争当中，掌握双语的父辈要加强子代双语教育，同时学校加强双语教学有利于弱势语言冲破濒危灭绝的命运，通过提高双语学习的氛围，增加子代学习双语的热情和机会，语言学习热情的提高促进语言学习的主动性，促使人们自觉使用学习新语言进行交流，促进弱势语言一部分通过双语的形式保留下来，另一部分以母语保留下来。

5.4学习率对人口比例以及词汇的影响

学习率是个体通过交流获得词汇的可能性，提高词汇学习率有利于弱势语言通过双语的形式保存。图19中将学习率提高3倍，由原来的5%提高到15%后，改变了最终只有强势语言保留的趋势，继而转变成强势单语A人口比例下降，而双语AB人口比重上升，弱势单语B主要以双语形式保存。由此可知，学习率的提高，可以促进只掌握强势单语的个体学习其它语言的积极性以充实自己，弱势语言得以依附于双语者而留存。学习率的提高可以促进人们学习弱势语言的积极性，将原来强势单语者转变成双语者，从而使得弱势语言得以保存。

网络中的个体的语言交流首先满足被交流个体在交流个体的社交范围内，同时要满足交流概率(pcommunication)才能进行语言的交流。当达到上述条件时，进行语言内部的词汇交流和学习，设定p为学习率，q为遗忘率，词汇的学习概率与语言地位成正比，而词汇的遗忘与语言成反比。由图20中可以看出，与提高语言学习率之前的图19a比较，图19b的仿真结果中提高词汇学习率后弱势单语B词汇最终并不会消亡，弱势语言词汇量有一定提升，并能稳定在一个阈值范围内稳定共存。图21熟练度模型中，随着学习率的提高，两种语言的熟练度都有提高，提高语言学习率可以促进个体学习该语言的积极性，语言学习积极性的提高就会促进该语言的交流频次的提高。因此，词汇学习率的提升，可以提高个体学习除母语以外的语言(词汇)的积极性和主动性，思想上改变人们学习语言的被动性，由不自觉走向自觉学习语言，使得弱势单语主要以双语的形式保留下来，改变弱势单语的濒危消亡的现状。

5.5综合对比

以现实社会中的某一局部区域为例，区域内的两种单语(汉语和少数民族语言)语言地位经过长期演化竞争已经逐渐稳定，汉语语言地位sA=0.55，少数民族语言地位sB=0.45；地区内的人口分布以及社会交往半径基本固定(15，25，35)；模型同时调整双语遗传率pbilingual和语言学习率p，观察两者共同作用对语言的保护情况。学习率和双语遗传率分3组情况：1)pbilingual=20%,p=5%;2)pbilingual=50%,p=15%;3)pbilingual=80%,p=30%。

由图22、图23和图24可知，随着语言(词汇)学习积极性不断增加(提高学习率)，学校加强双语教学以及家庭加强对后代的双语教育(提高双语遗传率)，无论弱势语言还是优势语言能够在局部区域内稳定共存，两种语言的词汇量也随着学习率的提高而逐渐增加并稳定在一个较高的词汇掌握量，伴随着语言交流频次的提高，语言使用的热度也在一个较高水平。

6结论

本文利用基于agent的社会圈子网络理论构建结构上更接近实际社会网络的动态语言竞争网络,网络中的agent赋予词汇结构,即利用两个长度为F的二进制位串表示其可能掌握的语言内部结构，同时给出了agent间由语言地位和语言交流机会共同决定的词汇学习和遗忘概率计算公式以及父辈遗传子代继承词汇的计算方法，构建了一种新的复杂agent动态网络微观语言竞争模型。模型重点描述了具有不同语言地位的agent之间通过交流实现词汇的学习和遗忘，反映agent所掌握的语言类型、词汇量及其熟练度的变化过程，根据不同人群词汇量的掌握情况以及语言熟练度进一步细化模型，进而反映出不同语言者通过交流和竞争实现语言内部微观结构演化涌现所表现出的不同语言类型之间的宏观竞争态势。模型研究表明：1)空间封闭与隔离有利于语言的保护，扩大人口的交往范围和人口流动趋势给弱势语言保存带来了严峻的挑战。在城市化进程中要尽量做到“离土不离乡”，尽力保护民族地区的社会文化结构，构筑少数民族经济和文化的内向型社会，从而保护濒危语言交流的环境。2)语言地位对语言保护至关重要。在当前社会经济环境下，少数民族人员的母语和保护意识需要从以前的不自觉变为自觉，需要通过教育宣传措施增强语言和文化的自豪感和自信心，促进语言和文化自觉。3)加强学校和社会的双语教育力度，提高弱势语言的学习效率，促进弱势语言通过双语者的方式保留下来。4)加强父辈的双语遗传教育力度，除了提高弱势语言保存力度外还可以提高个体在社会中的竞争力和生存能力。实验结果所反映结论显示具有内部词汇结构的微观语言竞争模型所得出结论与之前宏观模型所反映的社会现象相一致。模型中影响词汇学习和遗忘概率公式较简单，语言种类较少，进一步需要将影响社会的因素加入公式综合考虑以便更加贴合实际社会。

参考文献:

[1]徐世璇. 濒危语言研究[M]. 北京:中央民族大学出版社,2001.

[2]郭兰英. “适者生存”：翻译的生态学视角研究[D]. 上海：上海外国语大学,2011.

Guo Lanying. “Survival of the fittest”: ecological perspective in translation studies[D]. Shanghai: Shanghai International Studies University,2011.

[3]Beckner C, et al. Language is a complex adaptive system: position paper [J]. Language Learning, 2009, 59(S1): 1-26.

[4]Abrams D M, Strogatz S H. Modeling the dynamics of language death [J]. Nature, 2003, 424:900.

[5]Mira J, Paredes A. Interlinguistic similarity and language death dynamics [J]. Europhysics Letters, 2005, 69(6):1031-1034.

[6]Minett J W, Wang W S Y. Modeling endangered languages: the effects of bilingualism and social structure [J]. Lingua, 2008, 118(1):19-45.

[7]Kandler A, Steele J. Ecological models of language competition [J]. Journal of Biological Theory, 2008, 3(2):164-173.

[8]Zhang M H， Gong T. Principles of parametric estimation in modeling language competition[J]. Proceedings of the National Academy of Sciences of the United States of America, 2013,110(24): 9698-9703.

[9]Lotka A J. Contribution to the theory of periodic reaction[J]. J Phys Chem, 1910, 14(3):271-274.

[10] Stauffer D, Castelló X, Eguíluz V M, et al. Microscopic Abrams-Strogatz model of language competition [J]. Physica A: Statistical Mechanics and Its Applications, 2007, 374(2):835-842.

[11] Castelló X, Eguíluz V M, Miguel M S. Ordering dynamics with two non-excluding options: bilingualism in language competition [J]. New Journal of Physics, 2006, 8(12):308-322.

[12] Li X, Chen G. A local-world evolving network model [J]. Physica A: Statistical Mechanics and its Applications, 2003, 328(1-2):274-286.

[13] Castelló X, Toivonen R, Eguiluz V M, Saramaki J, Kaski K, San Miguel M. Anomalous lifetime distributions and topological traps in ordering dynamics [J]. Europhysics Letters, 2007, 79(9):66006(1-6).

[14] Toivonen R, CastellóX, Eguiluz V M, et al. Broad lifetime distributions for ordering dynamics in complex networks [J]. Physical Review E, 2008, 79(1):016109.

[15] Hamill L, Gilbert N. Social Circles: A Simple structure for agent-based social network models [EB/OL]. Journal of Artificial Societies and Social Simulation (S1460-7425), 2009, 12(23):3.

[16] Kosmidis, Kosmas, Halley J M, et al. Language evolution and population dynamics in a system of two interacting species [J]. Physica A: Statistical Mechanics and Its Applications, 2005, 353(2):595-612.

[17] Schwammle V. Simulation for competition of languages with an ageing sexual population [J]. International Journal of Modern Physics C, 2005, 41(2):41-49.

[18] 戴庆厦. 云南里山乡彝族语言使用现状及其演变[M]. 北京：商务印书馆，2009.

[19] Wilensky U. NetLogo.Center for connected learning and computer-based modeling, Northwestern University, Evanston, IL,USA.[EB/OL]. [2011-08-08].http://ccl.northwestern.edu/netlogo.

(责任编辑李进)

Complex Agent Network with Vocabulary Structure Model for Language Competition Model

WANG Chao1,2, BI Guihong1b, ZHANG Shouming1a, YU Qunxiu1a

(1. a.College of Information Engineering and Automation, 650500, China;b. College of Electric Power Engineering, Kunming University of Science and Technology, Yunnan 650500, China;2. Tianjin Center for patent review of the Patent Office of the State Intellectual Property Office, Tianjin 300280, China)

Abstract：This paper proposes a new dynamic social network model to study the competition between two languages (language A and B), this model is based on agent modeling method and social circles theory, and this method also introduces a language structure with two F-length bit-strings vocabulary into the agent which is a node of the network. The evolutions of the average number of words of each language and mastery of the language for agents in the network were analyzed by changing the language states, the structure of social network and the probability of language learning and vertical transmission. The proposed model facilitates the study of the mechanisms of macro behavior which emerges from local interactions and language competition between agents and the evolution of internal language structure of speakers. The simulation result indicates that the model introduced here does account for two key factors, they are the chance and frequency of language usage which influence language competition and do not consider well in other models.

Key words：agent; social circle; dynamic network; internal structure of language; language competition

文章编号：1672—3813(2016)02—0053—14;

DOI:10.13306/j.1672-3813.2016.02.007

收稿日期：2014-10-12；修回日期：2015-07-09

基金项目：国家自然科学基金(61364022)

作者简介：王超(1989-)，男，天津人，硕士，主要研究方向为复杂系统与复杂网络建模与仿真。 通讯作者：毕贵红(1968-)，男，云南昆明人，博士，教授，主要研究方向为社会与经济系统仿真。

中图分类号：TP391.9

文献标识码：A