集群运动:唯像描述与动力学机制
2016-06-13狄增如韩战钢
李 耕,狄增如,韩战钢
(1.北京师范大学系统科学科学院,北京 100875;2.嘉应学院物理与光信息科技学院,广东 梅州 514015)
集群运动:唯像描述与动力学机制
李耕1,2,狄增如1,韩战钢1
(1.北京师范大学系统科学科学院,北京 100875;2.嘉应学院物理与光信息科技学院,广东 梅州 514015)
摘要:鉴于生物群体在空间中展现出的大规模集群运动已经成为集群行为研究的一大热点,从集群运动的唯像描述到动力学机制的逻辑线索展开综述。唯像描述部分中主要介绍“一致性序参量”、“集群对称破缺”、“集群规模分布”和“空间关联”等集群运动的唯像特征。它们大都具有定量的实证基础,有些还体现出一定的定量普适性(适用于多物种)。在动力学机制部分分别介绍“吸引与排斥”、“对齐规则”、“相互作用范围”、“个体异质性”和“相互作用的线性叠加”等微观规则,重点总结了基于轨迹追踪的机制推断成果。还特别着重区分实证与假设。通过这样的逻辑梳理,既描绘出“集群运动”这一新兴领域在不长的时间里积累的丰硕成果,又清晰地系统展现出我们在追求集群运动普适律的道路上已经走了多远,以及摆在面前的重要问题。
关键词:集群运动;唯像理论;动力学机制
0引言
作为新兴的复杂性科学研究对象,集群运动广泛存在于生命现象中,而且都表现出看起来非常相似的集群模式:某些沙漠黄蜂的睡眠聚集[1],蚂蚁、蜜蜂等社会性昆虫的集群协作[2],蝗虫的集群侵袭[3],鱼群的集群游动[4-5],响尾蛇和瓢虫等的冬季群聚[6],牛群、鱼群、枪乌鰂、鸟群、鹭群、鸥群、燕鸥群和蝗虫群等的集群向心运动[6-7],狐蝠[8]和某些鸟类[9-11]的集群逃生,墨西哥无尾蝙蝠的集群出巢[12],斑纹角马、帝王蝴蝶等的集群迁徙。这些跨越物种,甚至跨越门类的集群运动现象是否存在普适性?我们能不能用同样结构的方程来描述它们,而其运动模式的区别仅仅在于方程中某些项或者参数的不同?
比起描述现象,学者们更着迷于理解现象背后的行为机制。成千上万只椋鸟竟然像一个整体一样在天空舞蹈:到底是什么力量在指挥它们如此完美协调地完成复杂的飞行过程?抑或是根本不存在这样的“指挥中心”,而是个体仅依靠近距离相互呼应,从而在整体上涌现出如此奇观?学者们相信,大部分集群运动都是自组织过程。个体仅仅利用相对局域的信息做出行为反应,从而在整体上涌现出具有某种宏观集群特征的现象。尤其近二十年来,人们越来越热衷于尝试理解集群运动在个体相互作用层面上的自然规律。
除了上述集群运动的唯像描述和机制解释,其进化动因[6,13-15]以及工程应用[16-17]也同样成为学者们兴趣点。但这篇综述的重点不在于此,不做赘述。
2012年匈牙利物理学家T. Vicsek在Physics Reports上应邀发表综述“collective motion”[18],标志着集群运动已成为物理学新兴的令人着迷的研究方向之一。该综述大致从集群统计量、观测与实验,以及模型三方面介绍了集群运动的研究进展。与此不同,本综述将从集群运动的唯像描述到动力学机制的逻辑线索展开综述。唯像描述部分中主要介绍“一致性序参量”、“集群对称破缺”、“集群规模分布”和“空间关联”等唯像特征。他们大都具有定量的实证基础,有些还体现出一定的定量普适性。动力学机制部分将分别介绍“吸引与排斥”、“对齐规则”、“相互作用范围”、“个体异质性”和“多体相互作用形式”等微观规则,重点总结基于轨迹追踪的机制推断成果。本综述还特别着重区分实证与假设。例如,对齐规则[19-20](然在几乎所有的集群运动模型中都扮演重要角色,但该机制尚缺乏实证支持,甚至被证明在某些种类的鱼群中是不存在的[21-22]。通过这样的逻辑梳理,希望既描绘出“集群运动”这一新兴领域在不长的时间里积累的丰硕成果,又清晰地系统展现出我们在追求集群运动普适律的道路上已经走了多远,以及摆在面前的重要问题。
1集群运动的唯像描述
唯像理论,是指“解释物理现象时,不用其内在原因,而是用概括试验事实而得到的物理规律。唯像理论是试验现象的概括和提炼,但仍无法用已有的科学理论体系做出解释”[23]。对于集群运动,基于观察或者实验直接得到的宏观(群体)层面的规律,便是集群运动的唯像理论。然而,目前尚缺乏足够普适的唯像理论,在不同的实验条件下往往得到不同的规律:因而称之为集群运动的“唯像描述”更为妥当。
1.1一致性序参量和群体极化度
个体运动速度或者速度方向的“一致性”是集群运动的最典型特征,也是最为直观的集群运动特征。T. Vicsek等[19]受启发于铁磁相变,提出了描述集群运动某种宏观状态的一致性序参量va。它定量刻画了一个群体中不同个体运动速度(矢量)的一致性程度。该序参量的数学表达式见式(1):
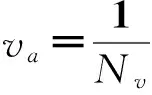
(1)
其中,N为粒子数,vi为第i个粒子的运动速度矢量。
另外,与之相类似,I. D. Couzin等[20]提出了“群体极化度”来描述个体运动方向的一致性(见式(2))。“一致性序参量”与“群体极化度”均只考虑了个体运动方向的一致性。
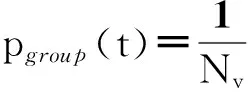
(2)
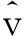
它的定量特征是:1)其值域为[0,1];2)当一个系统中所有粒子的运动方向全部相同,则该序参量的值为1;当每个粒子的运动方向被随机给定,则该序参量的值为一非零小量(随系统规模增加而趋近于零)。该研究还通过假设一种相互作用机制(见2.2节),得到序参量随群体密度或者随机扰动发生相变的结论。(注意到相变规律是在假设的动力学机制基础上推演而来的理论结果,其机制本身尚未得到实证支持;而关于密度相变的唯像规律得到一些并不严格的实证支持(见随后介绍的几项实证研究),因此并不能依此把这种相变纳入集群运动的唯像理论之中。)
B. Szabo等[24]通过电视显微镜实验研究了组织细胞的集群迁徙。他们直接采用了一致性序参量(见式(1))来度量群体中个体运动速度一致性。实验结果表明,当群体密度由低向高改变,群体运动发生从无序态走向有序态的相变(见图1);在临界密度附近,系统涌现出集群互动的复杂图像。如图2所示,a,b,c是实验截图,d,e,f是识别结果。可以看出,当密度较低时(a,d),群体做杂乱无章的无序运动;当密度较高(c,f),群体形成有序的一致性运动;而当群体密度在临界密度附近时(b,e),呈现整体无序而又有着内部结构的复杂模式。
J. Buhl等[25]在实验室环境下研究了沙漠蝗虫的集群运动,重点考察群体密度对瞬时对齐的影响。他们把蝗虫的运动限制在环形空间中。如果所有蝗虫都顺时针运动或者逆时针运动,那么这时群体的运动方向一致性最强。这种一致性由他们提出的物理量“instantaneous alignment”来度量,实际上可以把它看成在一维周期边界空间条件下的一致性序参量。如图3所示,a,b,c分别为不同密度的群体一致性随时间的变化过程。d,e,f则是相应密度下蝗虫个体相对中心参考点的角位移随时间的变化过程。实验结果表明,随着群体密度的增加,系统从无序运动状态快速变化到方向高度一致的有序运动状态。
借助于先进的测量技术,A. Cavagna等[26]从2005年到2007年在罗马用摄像系统多次捕捉了大规模紫翅椋鸟的集群飞行。图4A展示了一个椋鸟群体集群飞行的瞬时,每一个个体的运动速度矢量。这些记录到的不同群体包含了122到4 268个个体。他们发现所有24个群体的飞行都显示出极高的极化度:0.96±0.03(SD)。
1.2群体角动量
集群运动除了展现出群体中个体运动方向高度一致的有序态之外,有时还呈现出一致性旋转(同时顺时针或者逆时针)的有序态。该现象常见于某些海洋鱼群以及某些蝙蝠群体等。I. D. Couzin等[20]定义了“群体角动量”来定量刻画群体的旋转程度(公式(3))。

(3)
其中,
(4)
并且,
(5)
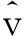
1.3集群对称破缺
对称破缺是又一种有趣的集群现象。E. Altshuler等[27]受D. Helbing等[28]的启发,发现蚂蚁群体存在群体逃逸的对称破缺。他们把一种蚂蚁群体放入一个左右两边有着对称出口的圆形空间中,在空间中央滴入一种驱虫剂,蚂蚁们便会相继从出口逃出。神奇的是,从左右两边逃出的数目并不对称(见图5)。
他们用百分比差来度量这种对称破缺:
(6)
其中,L和R分别为一次实验中从左边和右边逃出的蚂蚁总数。并试图进一步用实验方法考察密度对于对称破缺的定量影响,但没有得到可靠的结果。
G. Li等[29]考虑了随机性对这种对称破缺的影响,并从上面的定义中消除了这种由随机性引致的不对称性,定义了“集群对称破缺”。并用和E. Altshuler类似的实验方法得到了集群对称破缺关于密度的变化曲线(见图6)。结果表明集群对称破缺随群体密度先增加后逐渐衰减。
1.4集群规模与集群数量
从集群规模分布的研究中,我们看到了一点普适性的曙光:同一个集群规模分布函数形式适用于某种细菌、几种鱼群,还可能包括非洲水牛群体。
E. Bonabeau等[30-31]介绍了不同种类的鱼群和非洲水牛的集群规模分布。如图7所示,图7a为鱼群的集群规模分布图,为双对数曲线。图7b的“+”表示非洲水牛的实际分布,通过直接数数获得;两条虚线分别是幂律分布拟合和指数分布拟合,展示出先幂律后指数尾的分布特征。
H. P. Zhang等[32]研究了野生型枯草芽孢杆菌的集群运动:这些细菌会自发地聚集成集团并有序地运动。
他们讨论了群体规模的分布函数P(n)。如图9所示,正方形、圆形和三角形分别表示3种不同菌群密度下的结果。可见P(n)随着n的增加先以幂率衰减(见图9中的小图),然后变成一个指数尾(图9中的大图)。最终得到P(n)的定量表达式,见式(7):
(7)
重新标度规模大小后的规模分布曲线全部重合在一起(见图9中的小图)。
1.5空间关联
不仅群体规模分布,集群运动中的个体运动状态关联也显示出普适性。A. Cavagna等[26]为了深入了解集群响应,研究了个体速度波动之间的关联:
(8)
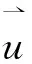
(9)
δ(r-rij)为平滑狄拉克δ函数,c0为归一化因子。关联函数度量了相互距离为r的个体对的速度波动的平均内积。计算发现,椋鸟群的速度波动关联随着r的增加从1变化到-1(见图10a)。进一步研究表明,关联长度ξ随着群体规模的增加而线性增加(见图10c)。其定义为
C(r=ξ)
(10)
不仅如此,对于所有的飞行事件,用重新标度后的关联函数全部很好地重合在一起(见图11),表明这些速度波动关联是无标度的。椋鸟群不仅速度波动关联具有无标度性,其速率波动关联也具有同样的无标度特征(见图10b、10d)。
H. P. Zhang等[33]在野生型枯草芽孢杆菌的研究中同样发现了这种关联无标度特征。如图12所示,a,b;c,d;e,f和g,h分别是运动方向、速度、速率以及朝向的关联函数(a,c,e,g)以及重新标度距离后的关联函数(b,d,f,h)。发现所有这些不同运动状态量的关联长度都随集群规模的增加而线性增加;并且其函数曲线几乎相互重合。这说明细菌集群运动的速度、方向、速率以及朝向的波动均具有无标度性。
可以清晰地看到,运动状态关联无标度的唯像规律既存在于细菌集群运动又同样存在于椋鸟集群运动中。
除了研究集群运动中关联无标度性,H. P. Zhang等[32]还研究了细菌集群运动的其他空间关联特征,得到了一些十分有趣的唯像规律。空间关联由“配对关联”、“方向关联”和“速度关联”3个物理量来共同定量刻画。配对关联函数的数学表达式为
(11)
它表示的是在距离参考个体(x,y)的地方找到另一个个体的几率密度。方向关联和速度关联也由类似的表述来定义。如图14所示,a~c和d~f分别表示低密度和高密度条件下,配对关联、朝向关联和速度关联3种关联函数。颜色棒的值等于关联函数的值。g~i图中的曲线表示函数。其中黑线和灰线分别表示低、高密度条件下的函数曲线。
从图8可以看出,细菌群体存在多个集群。为了解同一集群中的空间关联,把细菌群体划分为若干个子群,对于每个子群单独计算关联函数g(x,y,n)(见图15)。其中n表示该集群中包含细菌的个体总数。采用g(x,y,n)=0.1的解来标度一个集群的所谓“统计边缘”(见图15a中的细黑线),并画出该解曲线与坐标轴的交点和与n之间的函数关系(见图15d)。黑色虚线为所拟合的幂函数曲线:
λ∝n0.5
(12)
2集群运动的动力学机制
微观机制的科学性大致取决于两点:它本身得到什么程度的实证支持,由机制推演出的理论结果得到什么程度的实证支持。长久以来,集群运动的实证研究受限于定量观测技术[34],大多数研究局限于定性观测研究或者用多个体模拟的方法,通过假定一些机制来研究集群运动。如今高速摄像技术及定位系统的发展使得获取密集的坐标时间序列成为可能[35],进而直接统计分析动力学机制。另一方面,几乎同样重要的是机制的“必要性”:我们不仅要求动力学机制的“真实性”,还期望它是产生集群运动现象的“必要”机制。
2.1吸引与排斥
吸引机制对于维持集群运动来说,看起来是必不可少的;否则群体会不断发散到更广阔的空间中。相互排斥则是必然存在的机制:每个个体都占据一定的空间,彼此不能相互穿越。但排斥是影响集群运动性质的必要机制吗?目前还没有确切的答案。
Y. Katz等[21]和J. E. Herbert-Read等[22]分别独立完成了鱼群自由集群游动的实验室研究,并得出了相似的结论。他们通过控制水深,把鱼群限制在近似二维平面上游动,用摄像设备录制了鱼群的游动过程,并较好地实现了群体中所有个体的轨迹追踪。这使得他们得以获取每一个体的坐标时间序列。
当鱼群总数N=2时,它们仍能协同一致地游动。把一条鱼作为参考点,考察另一条鱼的空间分布,并统计另一条鱼的受力关于其位置的函数。如图16所示,“BL”表示鱼的体长。颜色棒表示力的大小和方向,例如,A方向表示正向力,B方向表示反向力。
这样便可以知晓当个体B处于参考个体A的不同位置的时候,个体A的受力情况。实际上就直接通过统计推断的方法获取了相互作用机制。把个体A的受力分解为沿着体长方向的“加速力”(见图17a)和垂直于体长方向的“转向力”(见图17b)。可以看出围绕着参考个体的前方和后方有一明显的“排斥区域”,离开参考个体较远的前后左右存在明显的“吸引区域”。这样就首次定量地描绘了鱼群集群动力学中的吸引力和排斥力。
2.2对齐规则
对齐规则早先提出者是C. W. Reynolds[36]。他为模拟生物集群运动提出了一套模型,其中一条便是对齐规则。模拟集群运动的著名模型,包括Vicsek model[19]和Couzin model[20]都包含了对齐规则。对齐规则要求群体中的每一个个体的运动方向都和自己一定范围内邻居的平均方向相一致。
H. P. Zhang等[32]分析了细菌的空间关联(见1.3节),统计发现细菌个体与较近的邻居之间存在较强的速度关联和方向关联(见图10),从而认为验证了对齐规则的存在。然而,Y. Katz等和J. E. Herbert-Read等(见2.1节)却发现对齐规则似乎并不存在于鱼群集群运动中。他们不仅考察了个体受力关于相对参考个体位置的函数,还研究了受力关于相对朝向(如图16所示)的函数[21-22],如图18所示。从图c和d可以看出,加速力和转向力都和相对于邻居的朝向关系甚微。这些结果显示,鱼的集群运动中似乎并不存在对齐规则本身;而相互对齐更有可能是吸引和排斥的共同调节结果。
一个多个体模型研究[37]向人们展示了一个没有包含对齐规则的简单模型如何涌现出多样化的集群运动。它的模型规则非常简单,且在不同参数空间下,群体可以展现出一致性运动、一致性旋转等各种不同的集群运动模式。这提示我们,对齐可能并不是集群运动的“必要”机制。
2.3相互作用范围
很难想象在一个大规模群体中,每个个体可以和其他所有个体进行交互。因此每个个体选择同哪些邻居相互作用自然成为集群动力学的一个重要问题。著名的Vicsek model和Couzin model及其各种变体都有着一个共同点,个体的相互作用范围是欧式空间中的一个常量。这似乎是一个自然的假设,然而却遭到了实证挑战。
2007年,M. Ballerini等[38]通过摄录椋鸟群获取其运动数据,进而统计分析得到这样的结论:椋鸟的相互作用距离并不是欧式空间距离,而是拓扑距离:每只椋鸟只和最近邻的若干个(固定数目)邻居发生相互作用。把群体中每只鸟指向自己最近邻的单位矢量平移到一起:所有矢量原点重合在同一点上,这样得到一张矢量密度分布图。这实际上是一张最近邻个体方位密度分布图。用“第n近邻”替代最近邻,这样可以随着n的变化依次得到多张图。他们展示了n=1和n=10的两张图(见图19)。0o表示最近邻个体在正前方,180o表示最近邻个体在正后方。
第一近邻的矢量密度分布有着显著的不均匀性,且呈现某种有结构特征;而第10近邻的分布却相当均匀,没有任何结构特征。他们定义了一个指标γ来定量描述这种不均匀性,并画出γ关于n的函数图像。
如图20所示,随着n的增加,矢量密度分布的不均匀性逐渐衰减。当n=6或者7的时候,达到一个不再随n而变化的稳态。三角和圆圈分别代表两个不同密度的鸟群,因此不论群体密度如何,相互作用似乎只涉及固定数目的邻居:这和一直以来固定相互作用范围的假设是不同的。
关于相互作用范围,除了固定距离和固定邻居数之外还有第3种观点:认为生物的选择性在相互作用对象的选择上起到关键作用[39-40]。然而该机制尚未得到任何实证支持。
2.4个体异质性
上面讨论的各种机制都暗含一点假设:每个个体都遵循同样的规则。实际上有没有可能群体中的个体的地位是不同的?比如,有的个体比另一些个体对其他个体的影响力更大;有的个体比另一些个体携带更多信息,等等。更为重要的是,是否正是这样的个体异质性的存在才产生了集群运动现象?
M. Nagy等[41]证明了鸽群集群运动中个体的异质性:存在层级的领导-跟随结构。他们在鸽子身上固定上GPS,从而获得其飞行轨迹数据。考虑个体i在t时刻的方向矢量与j在t+τ时刻的方向矢量之间的相关性,并把该相关性对于t的均值记为Cij(τ)。较大的Cij(τ)值意味着i和j个体间存在显著的领导-跟随机制。如图21所示,字母是每只鸽子的身份标识。箭头由领导者指向跟随者,箭头上的数据表示时间延迟τ。作者们认为在这种较小的群体中,相比于同质群体,具有层级组织的异质群体具有更高的飞行效率。
R. Freeman等[42]通过一个鸽群实验研究了个体异质性在鸽群集群飞行中起到的作用。他们把鸽子从离巢若干公里以外的地方放飞,用定位系统记录它们的飞行轨迹。把同一只鸽子放飞若干次,可以得到若干条轨迹。这些轨迹的差异性(波动性)反映了该个体对于自己路径决策的“信心”。这样可以对每个个体测量所谓的“信心”指标。当把一对鸽子一起放飞,发现这一对鸽子共同飞过的路径往往取决于更有“信心”的个体通常选择的路径。因此,研究认为鸽群的飞行路径选择很大程度上受到对于路径选择更具“信心”的个体。
I. D. Couzin等[43]做了一个多个体模型研究:在无信息携带群体中混入一定比例的信息携带个体,从而影响非信息携带者的运动方向。模型采用对齐规则作为核心动力学机制。结果显示,对于越大的群体,把信息传播至并在行为上影响整个群体所需要信息携带个体的比例越少。他们希望以此解释生物集群运动中的导航行为。该模型尚缺乏实证支持。
2.5相互作用的线性叠加
一直以来,集群运动的理论研究不约而同地隐含了一个假设:个体间的相互作用满足“成对相互作用”,即所有个体之间存在两两相互作用,并且满足力的线性叠加。Y. Katz等[21]的研究成果挑战了这一假设。他们首先从两条鱼集群游动中统计得出其相互作用结构(见图17,图18)。然后在此基础上依照成对相互作用的假设,理论预测出3条鱼集群游动的相互作用结构(见图22)。a,e描绘了把每一条鱼当做参考个体时,其他两条鱼的空间部分结构。b,f是实证统计得到的在a,e图空间分布下的相互作用结构。c,g是成对相互作用假设下的预测结果。d,h则是实证结果和预测结果之间的差。
作者认为,成对相互作用定性地预测了从两体到三体的相互作用结构;但定量上,实际相互作用的强度比预测结果有25~100%的增强。因此,成对相互作用的假设可能忽略了一些对于集群运动来说比较重要的机制。
3讨论
3.1普适性与特殊性
集群运动的广泛存在性让我们相信其底层规律的普适性。然而我们看到,不论是唯像描述还是动力学机制,虽然已积累了较为丰富的研究成果,但我们还远远无法写下哪怕是一条普适律来描绘或者解释大部分集群运动特征。然而我们刚刚在唯像层次上看到了一点点普适性曙光,小结如下:1)最具普遍性的唯像特征当然也是最直观的:具有较强的群体运动方向一致性,即一致性参量的值接近于1。这至少已在细菌、组织细胞、昆虫、鱼群和鸟群的定量研究中得到了实证(见1.1节)。2)运动状态关联无标度的唯像规律存在于细菌和椋鸟的集群运动中(见1.4节)。3)集群规模先幂律后指数尾的分布存在于鱼群和细菌群体中,也可能存在于非洲水牛群体中(见1.3节)。而寻找普适的集群动力学机制似乎难度更大:在两种鱼群中发现类似的吸引和排斥机制,并且都暗示了对齐规则不存在(见2.1节和2.2节)。
集群运动在不同物种身上表现出差异性特征。这些物种差异造成的特殊性有时是微不足道的,从而造就了普适律;而有时却足以影响集群运动的唯像特征。例如,当密度由低往高变化时,沙漠蝗虫和某种组织细胞的运动方向都展现出从无序向有序的变化过程(见2.1节);而对于某些鱼,仅仅2条鱼构成的群体便可以在较大空间中形成持久的集群运动(见3.1节)。
3.2模型研究的局限性
S. Weitz等[44]用一项研究向人们展示了目前模型研究方法的某种弊端。G. Theraulaz等[45]在实验室环境下研究了蚂蚁的一种自组织集群行为:搬运尸体。蚁群通常会把尸体搬运聚集在一起,成为一个由蚂蚁尸体组成的集团。他们定量研究了这种集团数量随时间的变化过程(见图23)。
这种蚁群自组织行为唯像描述背后的动力学机制是什么?文中的多个体模型很好地拟合了该唯像结果。然而在此之后S. Weitz和G. Theraulaz等[44]用6套不同的动力学机制构建了6个模型,模拟结果都同样好地吻合了上述唯像结果(见图24)。
前面提过,微观规则的科学性大致取决于两点:微观规则本身得到什么程度的实证支持,以及由微观规则推演出的理论结果得到什么程度的实证支持。这项研究告诉我们,如此程度的实证支持远远不够;更加精巧的实验和精密的测量尤其重要。
3.3唯像研究与机制研究
具有物理学背景的学者往往自然地从统计物理的视角来看集群运动。生物群体系统和物理粒子系统有一点区别是重要的:我们几乎没法直接研究物理粒子之间的相互作用(尤其在热力学建立发展的那个时代);但对于许多生物个体,我们能够直接研究其行为规则。例如,近年来较为“盛行”的统计推断行为规则的方法。我们已经通过这种方法获得了关于动力学机制的新的知识。然而正如前文中多次提及的,怎样知晓这些规则是否是产生宏观集群运动的核心规则?这时候我们发现,唯像研究是必不可少的。
3.4研究展望
要深刻理解群体大规模集群运动,前方的道路显然长且曲折。随着研究的深入和成果的积累,集群运动研究中的核心问题日益凸显。下面我们简要列举若干将来可能会重点研究并取得突破的问题:1)积累唯像描述,构建唯像理论。更多地积累不同物种的集群行为的唯像描述,进而发掘统一规律,构建唯像理论。目前已经发现的唯像层次的跨物种规律,例如集群规模分布等,是否具有更广的普适性?2)对齐规则的存在性。研究发现,“对齐规则”在鱼群集群运动中不存在(见2.2节)。然而“对齐规则”在所有的集群运动中都只是“吸引和排斥”的调节结果吗?3)相互作用邻居的选择。每个个体选择和哪些其他个体发生相互作用?是按照一定空间邻域选择邻居,还是固定最近邻居数目,抑或是按照诸如选择性注意等认知规则来选择邻居?4)个体异质性。如同排斥规则一样,个体异质性虽然必然存在,但它会是集群运动的必要因素吗?在鸽群自由飞行,动物大规模迁徙等集群运动中,倘若个体间完全同质,集群现象是否会发生根本性改变?5)相互作用是否满足线性叠加。鱼群集群运动的研究表明,除了成对相互作用的线性叠加,我们还丢失了一些重要的相互作用。6)研究更简单更基本的聚集行为。聚集是形成集群运动的必要机制。理解聚集行为也许是理解集群运动本质机制的关键。我们已经在这方面有了一些研究积累[46],并将继续深入开展下去。
参考文献:
[1]Evans H E. The Comparative Ethology and Evolution of the Sand Wasps[M]. Cambridge: Harvard University Press, 1966: 526.
[2]Hölldobler B, Wilson E O. The ants[M]. Cambridge: Harvard University Press, 1990.
[3]Uvarov B P. Behaviour, Ecology, Biogeography, Population Dynamics[M]. Grasshopper and Locust: a Handbook of General Acridology, Cambridge University Press, 1977.
[4]Parr A E. A contribution to the theoretical analysis of the schooling behavior of fishes[J]. Occasional Papers Bingham Oceanography Collection, 1927, 1: 1-32.
[5]Breder C M J. Studies on social grouping in fishes[J]. Bulletin of the American Museum of Natural History. 1959, 117: 399-481.
[6]Wilson E O. Sociobiology: the New Synthesis[M]. 北京: 北京理工大学出版社, 2008.
[7]Nakamura E L. Behavior of Marine Ainimals: Current Perspectives in Research[M]. New York: Plenum Press, 1972.
[8]Neuweiler G. Verhaltensbeobachtungen an einer indischen Flughundkolonie (Pteropus g. giganteus Brünn)[J]. Zeitschrift fur Tierpsychologie, 1969, 26: 166-199.
[9]Mohr H. Zum Erkennen von Raubvogeln, insbesondere von Sperber und Baumfalk, durch Kleinvogeln[J]. Zeitschrift fur Tierpsychologie, 1960, 17: 686-699.
[10] Murton R K. The Problems of Birds as Pests[M]. New York: Academic Press, 1968: 157-169.
[11] Goss-Custard J D. Feeding dispersion in some overwintering wading birds[M]∥Crook J H. Social Behavior in Birds and Mammals: Essays on the Social Ethology of Animals and Man: London. New York:Academic Press, 1970, 3-35.
[12] Davis R B, Herreid C F, Short H L. Mexican free-tailed bats in Texas[J]. Ecological Monographs, 1962, 32: 311-346.
[13] Ioannou C C, Guttal V, Couzin I D. Predatory fish select for coordinated collective motion in virtual prey[J]. Science, 2012, 337(6099): 1212-1215.
[14] Yang S C, Jiang S J, Jiang L, et al. Aggregation increases prey survival time in group chase and escape[J]. New Journal of Physics, 2014, 16: 83006.
[15] Brock V E, Riffenburgh R H. Fish schooling: a possible factor in reducing predation[J]. Journal du Conseil, Conseil Permanent International pour l' Exploration de la Mer, 1960, 25: 307-317.
[16] Jadbabaie A, Lin J, Morse A S. Coordination of groups of mobile sutonomous sgents using nearest neighbor rules[J]. Automatic Control, 2003, 48: 988-1001.
[17] Liu Z X, Guo L. Synchronization of multi-agent systems without connectivity assumptions[J]. Automatica, 2009, 45: 2744-2754.
[18] Vicsek T, Zafeiris A. Collective motion[J]. Physics Reports, 2012, 517(3-4): 71-140.
[19] Vicsek T, Czirók A, Ben-Jacob E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical Review Letters, 1995, 75: 1226.[20] Couzin I D, Krause J, James R, et al. Collective memory and spatial sorting in animal groups[J]. Journal of Theoretical Biology, 2002, 218: 1-11.
[21] Katz Y, Tunstrom K, Ioannou C C, et al. Inferring the structure and dynamics of interactions in schooling fish[J]. Proceedings of the National Academy of Sciences, 2011, 108(46): 18720-18725.
[22] Herbert-Read J E, Perna A, Mann R P, et al. Inferring the rules of interaction of shoaling fish[J]. Proceedings of the National Academy of Sciences, 2011, 108(46): 18726-18731.
[23] 唯像理论[EB/OL].[2014-05-22].http://zh.wikipedia.org/wiki/%E5%94%AF%E8%B1%A1%E7%90%86%E8%AE%BA.
[24] Szabo B, Szolosi G J, Gonci B, et al. Phase transition in the collective migration of tissue cells: experiment and model[J]. Physical Review E, 2006, 74: 61908.
[25] Buhl J, Sumpter D J T, Couzin I D, et al. From disorder to order in marching locusts[J]. Science, 2006, 312(5778): 1402-1406.
[26] Cavagna A, Cimarelli A, Giardina I, et al. Scale-free correlations in starling flocks[J]. Proceedings of the National Academy of Sciences, 2010, 107(26): 11865-11870.
[27] Altshuler E, Ramos O, Nunez Y, et al. Symmetry breaking in escaping ants[J]. The American Naturalist, 166: 643-649.
[28] Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic[J]. Nature, 2000, 407: 487-490.
[29] Li G, Huan D, Reohner B, et al. Symmetry breaking on density in escaping ants: experiment and alarm pheromone model[J]. Plos One, 2014, 9(12):e114517.
[30] Bonabeau E, Dagorn L, Freon P. Scaling in animal group-size distributions[J]. Proceedings of the National Academy of Sciences, 1999, 96: 4472-4477.
[31] Bonabeau E, Dagorn L. Possible universality in the size distribution of fish schools[J]. Physical Review E, 5220: 51-54.
[32] Zhang H P, Be'Er A, Florin E L, et al. Collective motion and density fluctuations in bacterial colonies[J]. Proceedings of the National Academy of Sciences, 2010, 107(31): 13626-13630.
[33] Chen X, Dong X, Be'Er A, et al. Scale-invariant correlations in dynamic bacterial clusters[J]. Physical Review Letters, 2012, 108(14):148101.
[34] Couzin I D, Krause J. Self-organization and collective behavior in vertebrates[J]. Advances In the Study Of Behavior, 2003, 32: 1-75.
[35] Dell A I, Bender J A, Branson K, et al. Automated image-based tracking and its application in ecology[J]. Trends in Ecology & Evolution, 2014, 29(7): 417-428.
[36] Reynolds C W. Flocks, herds and schools: a distributed behavioral model[J]. Acm Siggraph Computer Graphics, 2015, 21(4):25-34.
[37] Strömbom D. Collective motion from local attraction[J]. Journal of Theoretical Biology, 2011, 283(1): 145-151.
[38] Ballerini M, Cabibbo N, Candelier R, et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study[J]. Proceedings of the National Academy of Sciences, 2007, 105: 1232-1237.
[39] Romanczuk P, Schimansky-Geier L. Swarming and pattern formation due to selective attraction and repulsion[J]. Interface Focus, 2012, 2: 746-756.
[40] Lemasson B H, Anderson J J, Goodwin R A. Motion-guided attention promotes adaptive communications[J]. Proceedings of the Royal Society B, .2012, 280: 20122003.
[41] Nagy M, ákos Z, Biro D, et al. Hierarchical group dynamics in pigeon flocks[J]. Nature, 2010, 464(7290): 890-893.
[42] Freeman R, Mann R, Guilford T, et al. Group decisions and individual differences: route fidelity predicts flight leadership in homing pigeons (Columba livia) [J]. biology letters, 2011, 7: 63-66.
[43] Couzin I D, Krause J, Franks N R, et al. Effective leadership and decision-making in animal groups on the move[J]. Nature, 433: 513-516.
[44] Weitz S, Blanco S, Fournier R, et al. Modeling collective animal behavior with a cognitive perspective: a methodological framework[J]. Plos ONE, 2012, 7: e38588.
[45] Theraulaz G, Bonabeau E, Nicolis S C, et al. Spatial patterns in ant coloniespdf[J]. Proceedings of the National Academy of Sciences, 2002, 99: 9645-9649.
[46] Di Z, Gho M, Lu M, et al. How can one measure group cohesion? From individual organisms to their interaction[DB/OL]. http://arxiv.org/abs/1406.3595.
(责任编辑李进)
Collective Motion: Phenomenology and Dynamics
LI Geng1,2, DI Zengru1, HAN Zhangang1
(1.School of Systems Science, Beijing Normal University, Beijing 100875;2.School of Physics and Optical Information Science, Jiaying University, Meizhou 514015)
Abstract:From bacteria to vertebrate, collective motion in living groups in space has gradually become a research hot point. This paper reviews recent studies on collective motion according to the logic from phenomenology to dynamic mechanics. For the phenomenology study, we focus on “order parameter”, “collective symmetry breaking”, “group size distribution” and “spatial correlation” most of which are based on quantitative observations and experiments. Some of these rules are universal in the sense that they can be observed in various species. The “attraction and repulsion”, “alignment rule”, “interaction range”, “heterogeneity” and “linear superposition of interactions”, especially the inferred rules based on the traced tracks of various individual movements, are closely investigated in dynamics part of this paper. This review pays much attention to distinguishing observations and the experiment results from assumptions. Under this logic frame, not only the plentiful and substantial results in collective motion are reviewed, but also an explicit and clear picture is depicted on how many miles we have covered on pursuing the universal laws in collective motion and on what the most important problems are ahead of us.
Key words:collective motion; phenomenology; dynamics
文章编号:1672—3813(2016)02—0001—13;
DOI:10.13306/j.1672-3813.2016.02.001
收稿日期:2014-12-09;修回日期:2015-12-11
基金项目:国家自然科学基金(61074116,61374165)
作者简介:李耕(1985-),男,湖北丹江口人,博士研究生,讲师,主要研究方向为复杂系统中的群体行为。
中图分类号:N945
文献标识码:A
