基于重掺杂的谐振式传感器频率温度系数补偿研究

杨力建， 游卫龙， 张　磊， 杨　恒， 李昕欣

(1.复旦大学 专用集成电路与系统国家重点实验室，上海 200433;2.中国科学院 上海微系统与信息技术研究所 传感技术国家重点实验室，上海 200050;3.中国科学院 研究生院，北京 100040)



基于重掺杂的谐振式传感器频率温度系数补偿研究

杨力建1， 游卫龙2,3， 张磊2,3， 杨恒2， 李昕欣2

(1.复旦大学 专用集成电路与系统国家重点实验室，上海 200433;2.中国科学院 上海微系统与信息技术研究所 传感技术国家重点实验室，上海 200050;3.中国科学院 研究生院，北京 100040)

摘要:MEMS谐振式传感器具有精度高、准数字输出、抗干扰能力强等特点，高精度压力传感器、应力传感器等多采用谐振式工作原理。频率温度系数补偿是实现高精度谐振式传感器的关键技术。通过实验研究了利用重掺杂改善硅频率温度系数的技术。实验表明:P型掺杂浓度达到7×1019/cm3时，〈110〉晶向频率温度系数降低到-11.68×10-6/K；N型掺杂浓度达到6×1019/cm3时，〈100〉晶向谐振频率是温度的二次函数，在80 ℃左右频率温度系数有过零点。首次实验演示了利用低功耗加热控制结合N型重掺杂，当环境温度由30 ℃变化到40 ℃时，谐振频率温度漂移仅为1.13×10-7/℃。利用该技术可实现超高温度稳定性的谐振式传感器。

关键词：谐振式传感器； 振荡器； 频率温度系数； 温度补偿

0引言

谐振式传感器通过特定模态对能量和信息的集中与加强作用，可实现高灵敏、高稳定的传感[1]。多种高性能传感器如振动式陀螺[2]、高精度压力传感器[3]等均采用谐振工作方式。例如：日本横河电机的谐振式压力传感器[3]可实现0.01 %的测量精度，其温度系数小于常规硅基压力传感器的1/10(10×10-6/K)，是工业控制领域不可替代的关键传感器。另外，谐振器也是硅基微机电系统(MEMS)振荡器的核心单元。硅基MEMS振荡器是新一代振荡器，有望替代石英晶振在集成微系统中获得广泛应用[4，5]。据预测，今后几年内硅基振荡器市场的平均复合增长率将达65.2 %，是增长最快的MEMS器件之一。

提高温度稳定性是高精度谐振式传感器与硅基振荡器研究的一个主要学术问题。单晶硅扬氏模量的温度系数大，引起的谐振频率温度系数(temperature coefficient of resonant frequency，TCF)高达-30×10-6/K，比石英大2个数量级以上，极大增加了温度补偿的难度。

重掺杂无源补偿技术通过重掺杂直接改变单晶硅杨氏模量温度系数，可显著降低谐振结构的TCF，是实现高稳定谐振式传感器与硅基振荡器的重要方法。重掺杂改变半导体杨氏模量温度系数的效应是由于载流子在不同能谷间再分布引起的，其产生机制与压阻效应相似，存在显著的各向异性。早在20世纪60年代,Keyes R W等人就建立了该效应的能带模型[6]。1967年，Hall J J等人通过测量半导体中的声速得到了掺杂浓度为2×1019/cm3的N型硅刚性系数随掺杂浓度的变化[7]。

长期以来，由于硅杨氏模量的重掺杂效应并没有具体的应用，相关研究未获得进一步发展。近年来,随着谐振式传感器与硅基振荡器的迅速发展，硅杨氏模量重掺杂效应重新获得重视。乔治亚理工大学的Ayachi课题组在2009年利用硼重掺杂将〈110〉晶向谐振结构的频率温度系数由-30×10-6/K降低到-1.5×10-6/K[8]。丹佛大学的Hajjam等人在2010年采用N型重掺杂结合偏置电压补偿使〈100〉晶向谐振结构的频率温度系数小于100×10-9/K[9]。

本文利用一种I2Bar谐振器实验研究了重掺杂温度补偿技术，测量了掺杂浓度为6×1019/cm3的N型〈100〉晶向谐振结构和掺杂浓度为7×1019/cm3的P型〈110〉晶向谐振结构的频率温度系数。首次实验演示了利用低功耗加热控制结合N型重掺杂实现极低频率温度系数。实验测得，当环境温度由30 ℃变化到40 ℃时，谐振结构的频率漂移仅为1.13×10-7/℃。利用该技术可实现超高温度稳定性的谐振式传感器和硅基MEMS振荡器。

1I2Bar谐振结构设计

由于I2Bar结构[10]的共振频率由单一晶向的杨氏模量决定，便于精确测定特定晶向的TCF，本文采用I2Bar谐振器作为测试结构。I2Bar谐振器的俯视图如图1(a)所示。核心谐振结构为2根直拉直压的I梁支撑2个用作为电极的Bar形成I2Bar结构。在I2Bar结构两侧制作驱动电极，通过静电驱动使I2Bar结构谐振。采用压阻检测读出谐振信号。将两个锚点间的结构电阻用作为力敏电阻，工作时电路的流向如图1(a)中箭头所示，压阻信号主要由2根I梁的直拉直压振动决定。

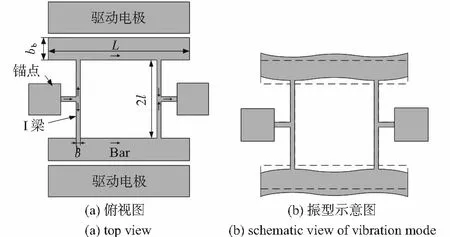
图1　I2Bar谐振器示意图Fig 1　Schematic view of I2Bar resonator

I2Bar谐振结构的振型如图1(b)所示。采用瑞利—里兹法可求得谐振频率为

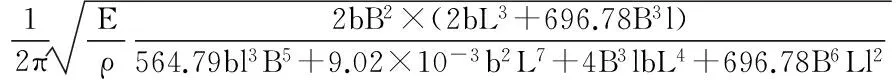
(1)

基于式(1)设计了N型和P型谐振结构，其尺寸、解析结果与ANSYS模拟得到的谐振频率如表1所示。解析结果与ANSYS模拟结果偏差小于10 %。

表1　N型和P型谐振结构尺寸、计算与ANSYS模拟得到的谐振频率

2制作流程

采用P型SoI硅片制作P型I2Bar谐振器，其工艺流程如下：

1)采用OKMETIC的P型〈100〉BESOI硅片，顶层硅厚度为5 μm，埋层氧化层厚度为2 μm，顶层硅为硼重掺杂，掺杂浓度为6×1018/cm3。

2)采用3次涂源预淀积和长时间再分布的方法[9]提高顶层硅掺杂浓度；每次预淀积温度为1 100 ℃，时间为60 min，共180 min；再分布温度为1 100 ℃，干氧200 min，湿氧30 min，干氧10 min，共240 min；采用SUPREM模拟得到掺杂浓度为7×1019cm-3，方块电阻为3.30 Ω/□；测得陪片方块电阻为3.4 Ω/□，与模拟吻合。

3)腐蚀去除表面氧化层，光刻谐振结构，采用DRIE刻穿顶层硅。

4)光刻铝电极图形，溅射铝，采用lift-off工艺形成铝电极。

5)采用HF蒸气腐蚀去除谐振结构下的氧化埋层，释放结构。

N型I2Bar谐振器采用重掺杂N型SOI硅片制作，顶层硅为磷重掺杂，掺杂浓度为6×1019/cm3，其制作流程与P型谐振器流程(3)～(5)相同。制成的N型和P型I2Bar谐振器如图2所示。

图2　样品照片Fig 2　Sample pictures

3频率温度系数测试

I2Bar谐振器的谐振信号采用压阻检测。为了降低检测电流对谐振结构的加热效应，压阻电桥电压V设为0.1 V。在真空腔中对谐振结构的幅频特性作了测量。真空腔压强为15 Pa时，测得的N型和P型谐振结构幅频特性如图3所示。N型直拉直压模态的共振频率为4 151 296.9 Hz，Q值为87 212。P型直拉直压模态的共振频率为4 013 817.5 Hz，Q值为144 970。谐振频率与理论值的偏差小于10 %。

对N型谐振结构的频率温度特性做了测量，结果如图4所示。测量中采用芯片上单晶硅梁作为温度传感器以精确测定温度。由图中可以看出，谐振器频率近似是温度的二阶函数呈现明显的非线性，在80 ℃左右有过零点。

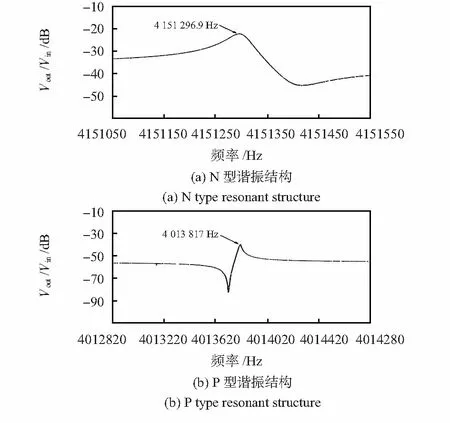
图3　幅频特性曲线Fig 3　Amplitude-frequency characteristic curves

图4　〈100〉晶向N型重掺杂谐振结构的频率温度特性Fig 4　Frequency-temperature characteristic curve of〈100〉 N type heavy doping resonant structure

利用该特性并结合恒温控制技术，有望实现高温度稳定性的硅基MEMS谐振器。对该方法进行了实验，通过在N型谐振器上通电流对谐振器加热，将谐振器温度升高到频率温度系数为0的点，此时谐振器两端电压为0.704 V，对应的加热功率为8.2 mW。然后改变环境温度，测得环境温度为30 ℃时谐振器频率为4 151 303.1Hz，40 ℃时谐振器频率为4 151 307.8 Hz，如图5所示，环境温度改变10 ℃频率漂移为1.13×10-7/℃。

P型谐振结构的频率温度特性测量结果如图6所示。由图中可以看出,P型重掺杂结构〈110〉晶向的频率温度特性是线性的，7×1019cm-3的重掺杂使TCF下降为-11.68×10-6/K。

图5　8.2 mW加热控制下且环境温度为30，40 ℃时谐振频率Fig 5　Resonant frequencies at 30,40 ℃ with 8.2 mW heating

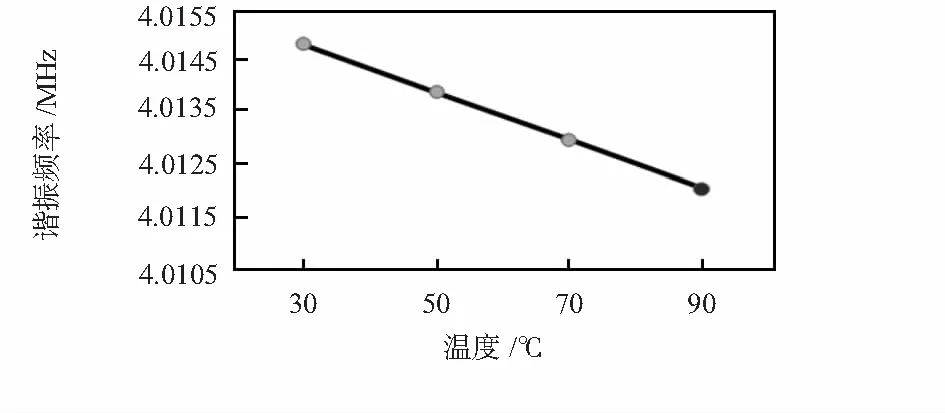
图6　〈110〉晶向P型重掺杂谐振结构的频率温度特性Fig 6　Frequency-temperature characteristic curve of〈110〉 P type heavy doping resonant structure

4结束语

本文设计并制作了掺杂浓度为6×1019/cm3的N型〈100〉和掺杂浓度为7×1019/cm3的P型〈110〉重掺杂硅基I2Bar谐振结构。实验测得:N型重掺杂谐振结构的谐振频率是温度的二阶函数，在80 ℃附近存在频率温度系数过零点。利用该特性并结合恒温控制技术，有望实现高温度稳定性的硅基MEMS振荡器。首次实验演示了利用低功耗加热控制结合N型重掺杂实现极低频率温度系数的方法，当环境温度由30 ℃变化到40 ℃时，谐振结构的频率漂移仅为1.13×10-7/℃。P型重掺杂谐振结构的频率温度特性为线性，7×1019/cm3的P型重掺杂使谐振结构的频率温度系数下降到-11.68×10-6/K，可用于静电反馈等温度补偿技术。

参考文献:

[1]BrandO.CMOS-basedresonantsensors[C]∥The4thIEEEConferenceonSensors,California,USA,2005:129-132.

[2]YazdiN,AyaziF,NajafiK.Micromachinedinertialsensors[C]∥ProceedingsoftheIEEE,1998:1640-1659.

[3]HaradaK,IkedaK,KuwayamaH,etal.Variousapplicationsofresonantpressuresensorchipbasedon3Dmicromachining[J].SensorsandActuatorsA,1999,73:261-266.

[4]vanBeekJTM，PuersR.AreviewofMEMSoscillatorsforfre-quencyreferenceandtimingapplications[J].JMicromechMicroeng,2012,22:013001.

[5]NguyenCTC.MEMStechnologyfortimingandfrequency[J].IEEETransUltrasonFerroelectrFreq,2007,54(2):251-270.

[6]KeyesRW.Electroniceffectsintheelasticpropertiesofsemiconductors[J].SolidStatePhysics,1967,20:37-89.

[7]HallJJ.ElectroniceffectsintheelasticconstantsofN-typesilicon[J].PhysicalReview,1967,161:756-761.

[8]SamaraoAK,AyaziF.Temperaturecompensationofsiliconmicromechanicalresonatorsviadegeneratedoping[C]∥The2009InternationalElectronDevicesMeeting,Maryland,USA,2009:789-792.

[9]HajjamA,RahafroozA,PourkamaliS.Sub-100ppb/℃temperaturestabilityinthermallyactuatedhighfrequencysiliconresonatorsviadegeneratephosphorousdopingandbiascurrentoptimization[C]∥The2010InternationalElectronDevicesMeeting,California,USA,2010:170-173.

[10]HoGK,SundaresanK,PourkamaliS,etal.Low-motional-impe-dancehighly-tunableI2resonatorsfortemperature-compensatedreferenceoscillators[C]∥The18thIEEEInternationalConfe-renceonMicroElectroMechanicalSystems,Florida,USA,2005:116-120.

Study on temperature coefficient compensation of frequency of resonant sensor based on degenerate doping

YANG Li-jian1， YOU Wei-long2,3， ZHANG Lei2,3， YANG Heng2， LI Xin-xin2

(1.State Key Laboratory of ASIC & System，Fudan University，Shanghai 200433，China;2.State Key Laborary of Transducer Technology，Shanghai Institute of Microsystem and Information Technology，Chinese Academy of Sciences，Shanghai 200050，China; 3.Graduate University of Chinese Academy of Sciences,Beijing 100040,China)

Abstract:MEMS resonant sensor has features of high precision,quasi digital output and strong anti-interference.High precision pressure sensors and strain sensors most adopt resonant working principle.The compensation of temperature coefficient of frequency (TCF)is one of the key issues to realize high precision resonant sensors.Compensation of silicon temperature coefficient of frequency with degenerate doping has been studied by experiments.It is shown by experiments that temperature coefficient of resonant frequency in 〈110〉 orientation decreased to -11.68×10-6/K by 7×1019/cm3 P+ doping;resonant frequency in〈100〉orientation is quadratic function of temperature after 6×1019/cm3 N+ doping,temperature coefficient of resonant frequency crosses zero point at about 80 ℃.It has been shown for the first time that the resonant frequency temperature drift is only 1.13×10-7when the ambient temperature changes from 30 ℃ to 40 ℃ with low power consumption heating control combined with N type degenerate doping.Resonant sensors with ultra high temperature stability can be developed with the technique.

Key words:resonant sensor; oscillator; temperature coefficient of frequency(TCF); temperature compensation

DOI:10.13873/J.1000—9787(2016)02—0039—03

收稿日期：2015—05—08

中图分类号：TP 212.1

文献标识码：A

文章编号：1000—9787(2016)02—0039—03

作者简介:

杨力建(1985-)，男，河北石家庄人，硕士研究生，主要研究方向为传感器和微机电系统。