行人惯性导航零速检测算法*

费程羽， 苏　中， 李　擎

(北京信息科技大学 高动态导航技术北京市重点实验室，北京 100101)



行人惯性导航零速检测算法*

费程羽， 苏中， 李擎

(北京信息科技大学 高动态导航技术北京市重点实验室，北京 100101)

摘要:在行人惯性导航中，零速检测是实现速度误差清零和导航误差估计的前提，有着重要的作用。针对行人运动过程中零速区间时间间隔短难以检测的问题，提出了一种基于人体脚部运动特征的零速检测算法，将步行运动抽象成了一个包含4个隐含状态与15个观测量的隐马尔可夫模型，并阐述了模型构建机理。利用Baum—Welch算法训练和优化模型参数，提高了检测准确率。实验结果表明：所提出的方法零速检测效果较好，且采用该方法的行人惯性导航系统，其定位误差约为行进距离的0.73 %，定位精度较高。

关键词：行人惯性导航； 零速检测； 隐马尔可夫模型； Baum—Welch算法

0引言

现有的行人惯性导航中绝大多数采用惯性导航计算位置，并设置零速修正算法消除速度积累误差[1～4]。所谓零速修正算法是指在行人运动过程中的零速区间内利用卡尔曼滤波器估计导航误差，抑制位置与速度误差的发散的方法。由于行人步行运动过程中脚部接触地面的时间即零速区间时间很短(通常为0.1～0.3 s)，因此，如何准确可靠地检测零速区间成为了一个重要问题。

将步行运动按照脚的状态进行划分，如果每一步中脚的不同状态均能够被有效检测，那么,就可以得到准确的零速区间，依据这种思想,本文提出了一种基于隐马尔可夫模型的零速检测算法，将行人的步行运动过程抽象为一个隐马尔可夫模型，并利用Baum—Welch算法训练和优化模型参数，从而实现的运动过程中的零速检测。

1行人的步行运动特征

对于行人的步行运动而言，在运动中的任意时刻至少有一只脚处于与地面接触状态，所以，按照步行过程中脚的运动状态，可以将一个步行周期大体分为两个阶段：静止阶段与摆动阶段。摆动阶段又可以分为三部分，即前脚尖离地、空中摆动、后脚跟着地三个过程，因此,将一个步行周期分为前脚尖离地、空中摆动、后脚跟着地与全脚掌着地4个过程。为了获取行人运动的惯性信息，探索行人的步行运动特性，将惯性测量单元(IMU)安装于行人的脚部，记录行走运动过程的加速度与角速度信息，设置采样频率为200 Hz，以保证记录的数据能够真实地反映全部步行运动过程。IMU的安装位置与轴向如图1所示。

图1　惯性测量装置Fig 1　Inertial measurement unit

通过实验发现，行人在步行运动过程中，其三轴加速度与三轴角速度均存在一定的周期性变化规律，总体来说，x轴角速度(如图2)的周期性特征更为明显，且输出曲线变化更为平缓，易于特征提取，因此,选取x轴角速度为后续的隐马尔科夫零速检测模型的观测量。

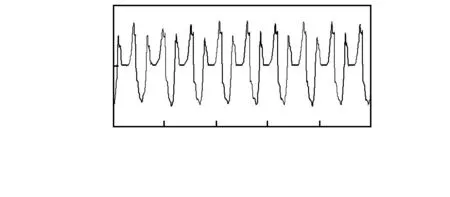
图2　x轴角速度Fig 2　x-axis angular velocity

2零速检测算法

对于行人步行运动，其存在两个随机过程:一个是惯性加速度与角速度的测量，这是一个可见的过程；另一个是步行运动中4种状态的传递过程，这是不可见的，但每个状态通过可能的x轴角速度输出记号，有了可能的概率分布。

2.1隐马尔可夫模型

隐马尔可夫概率模型具有模型参数。充分定义模型，需要以下元素[5]：

1)隐含状态数N；

2)每个隐含状态下可观测向量数M；

3)隐含状态转移概率矩阵A={aij}

aij=P{qt+1=j|qt=i},1≤i,j≤N,

(1)

式中qt为t时刻的状态，aij为状态i到状态j的转移概率，并且应满足正态随机约束

aij≥0,1≤i,j≤N,

(2)

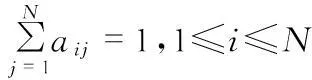
(3)

4)输出概率分布B={bj(Oi)}，bj(Oj)为与状态j相关的有限高斯分布

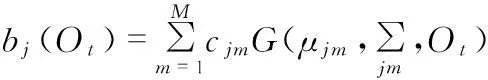
(4)

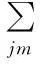
5)初始状态概率分布π={πj}，表示在初始时刻t=1时，观察向量的概率分布

π=P(q1=i),1≤i≤N,

(5)

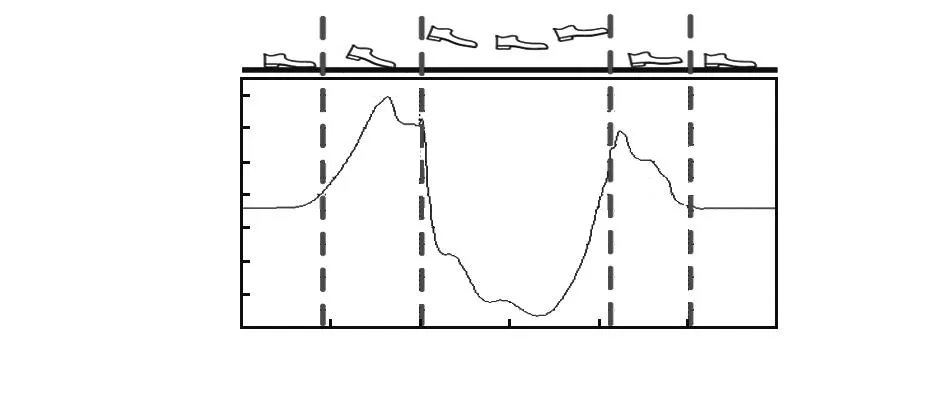
图3　模型状态与观测向量的定义Fig 3　Definition of model state and observation vector

在行人的步行运动过程中，理想的状态传递过程是A→B→C→D，然而，由于行人的运动存在一定的随机性，加上外部因素的干扰，状态传递往往不是在理想的情况下进行的，因此,需要调整初始状态转移概率矩阵的矩阵参数，经过实验分析得到调整后的初始状态转移概率矩阵A[6]

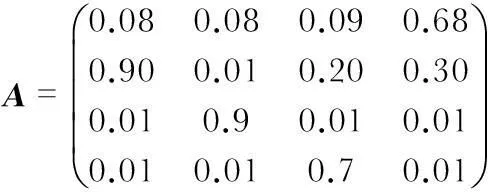
(6)

观测概率为每个观测值中出现隐含状态(状态A,状态B,状态C和状态D)的概率，为了获取初始的观测概率，需利用统计学方法处理观测样本。由于原始的角速度数据不能直接作为观测样本，因此，需要对其进行一系列的处理，处理流程如图4所示。

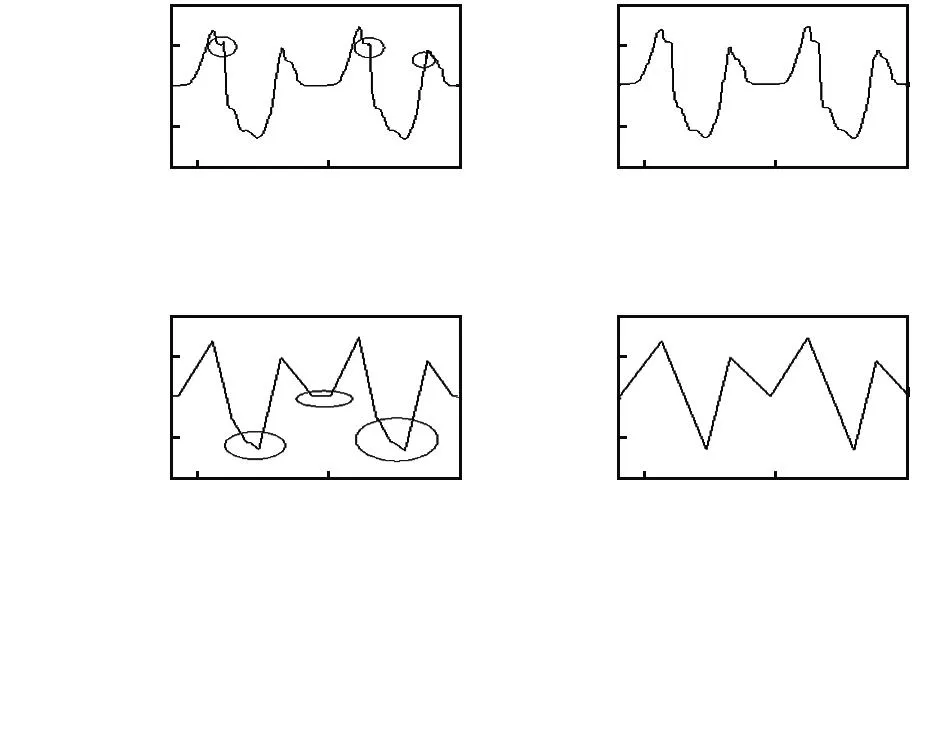
图4　观测向量提取算法流程图Fig 4　Flow chart of observation vector extraction algorithm

如图4所示，由于原始的角速度数据存在尖峰(如图4(a)圆圈内)，因此,首先采用平滑滤波处理数据得到滤波后的数据(如图4(b))，然后对滤波后的数据进行峰值提取得到仅保留峰值的数据(如图4(c))，但由于同一个状态内存正在多个峰值(如图4(c)圆圈内)不利于状态的统计，所以,将同一状态内多余的峰值进行滤除仅保留绝对值最大的峰值(如图4(d))。最后将处理后的角速度数据按照不同的观测值进行区域划分(如图5)，统计每个状态落在不同观测值区域内的概率。统计结果如表1所示。

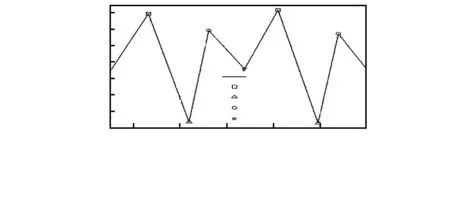
图5　观测值区域划分Fig 5　Observation value region division

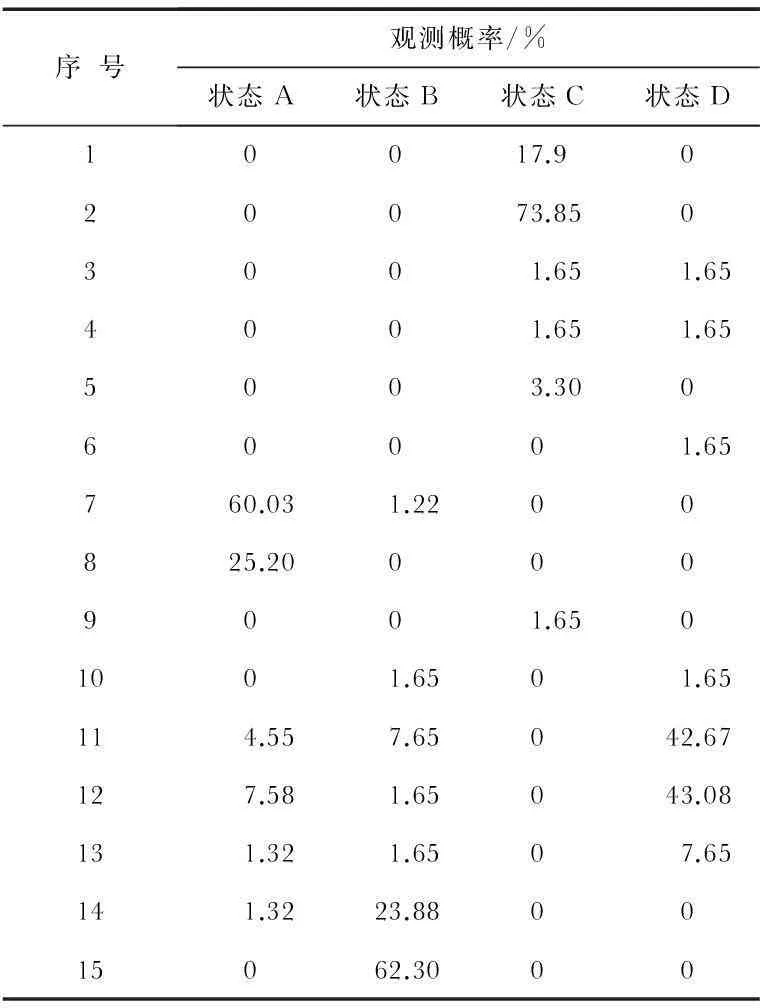
序号观测概率/%状态A状态B状态C状态D10017.9020073.8503001.651.654001.651.655003.30060001.65760.031.2200825.200009001.6501001.6501.65114.557.65042.67127.581.65043.08131.321.6507.65141.3223.880015062.3000

2.2模型参数优化

状态转移概率与观测概率初始化完成后，利用Baum—Welch算法优化模型参数。Baum—Welch算法是一种广义的期望最大化算法，算法流程如下[5]

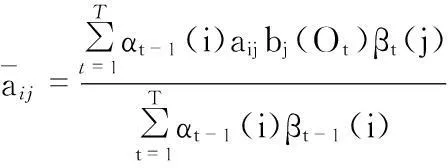
(7)

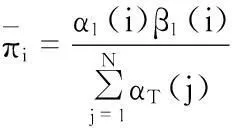
(8)

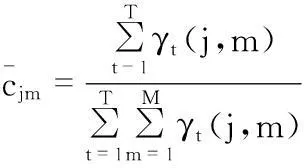
(9)

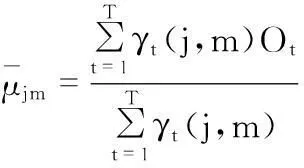
(10)

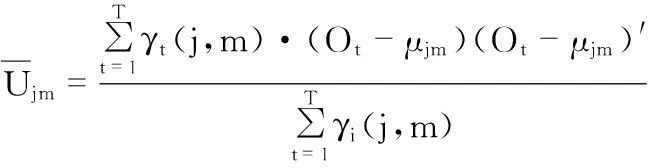
(11)

γt(j,m)=

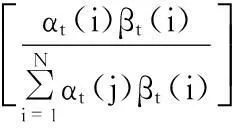
(12)

优化后的状态转移概率矩阵A1为

(13)

优化后的状态转移流程如图6所示，优化后的观测概率如表2所示。

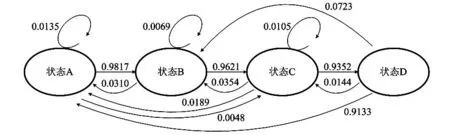
图6　状态转移流程图Fig 6　Flow chart of state transition

3行人惯性导航系统框架

行人惯性导航系统中广泛采用的系统架构是由Eric Foxlin[1]提出的，即利用安装于脚背上的惯性传感器所输出的数据进行捷联解算与零速检测，并利用零速检测结果触发卡尔曼滤波器来估计系统的状态误差，然后反馈校正捷联解算误差，实现行人的定位导航。

本文中利用所提出的基于隐马尔可夫模型的零速检测方法替换原框架中的零速检测部分，所构成的新行人导航系统框架如图7所示。

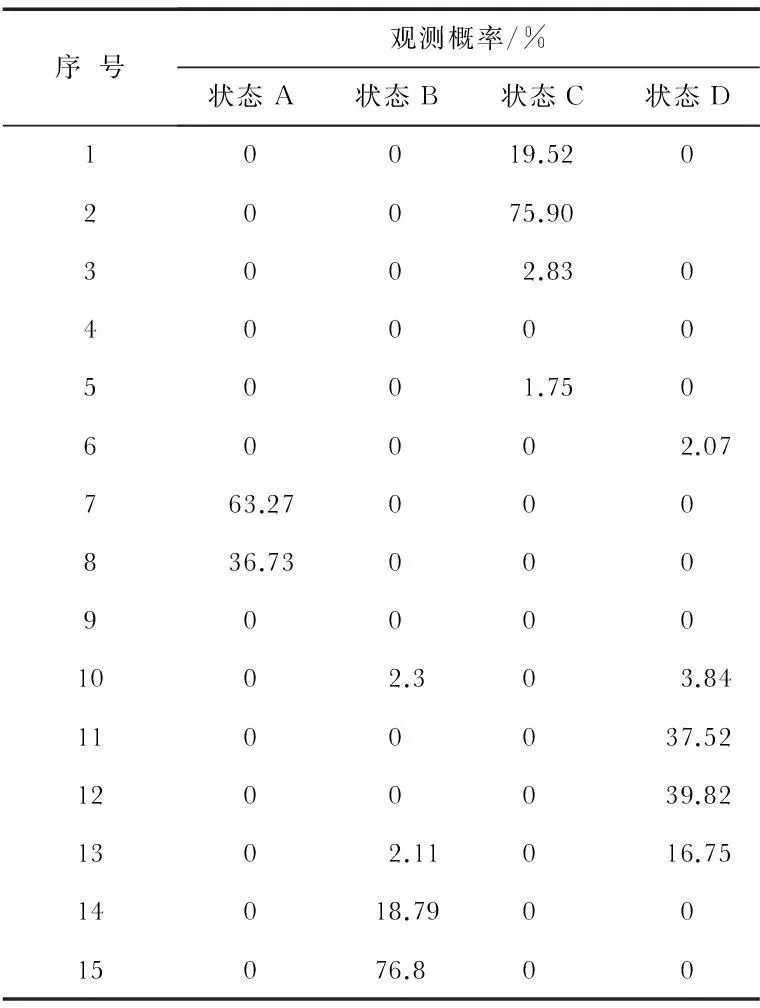
表2　优化后的观测概率

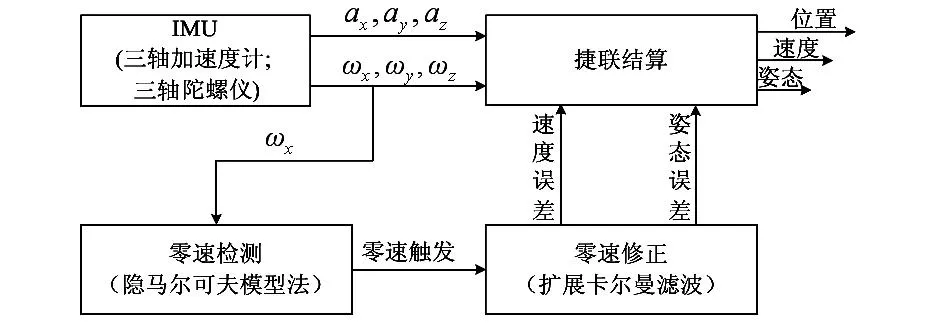
图7　行人惯性导航系统框架Fig 7　Framework of pedestrian inertial navigation system

4实验设置与结果

为了验证本文所提出的隐马尔可夫零速检测算法的性能，用三条件零速检测算法(C3)[2]的检测结果作为参考量，实验中设定的三条件算法参数分别为：加速度模值在阈值thamin=9.5 m/s2和阈值thamax=10.8 m/s2之间；加速度方差小于阈值thσa=1.3 m/s2；角速度模值小于阈值thω=50°/s。

利用两种零速检测算法分别对采集到的行人步行运动数据进行零速检测，检测效果的对比图如图8所示。

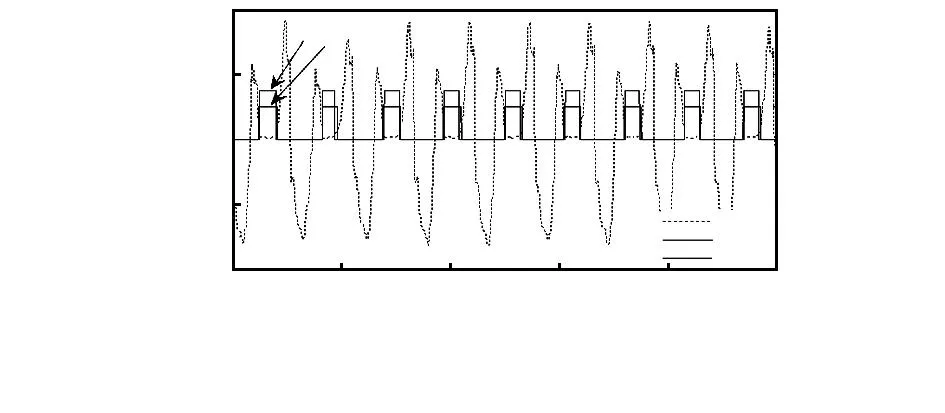
图8　检测效果对比Fig 8　Test effect contrast

通过实验可以看出：当行人进行步行运动时，本文提出的算法与三条件法的零速检测效果基本一致，均能够有效地检测出行人运动过程中的零速区间，但三条件法在计算过程中需同时用到三个轴加速度与角速度数据，而本文所提出的算法仅需要x轴的角速度数据即可，减小了计算量与计算时间。为了进一步验证零速检测算法在行人导航系统中的应用效果，进行了闭合曲线行走实验，行进轨迹显示如图9所示。

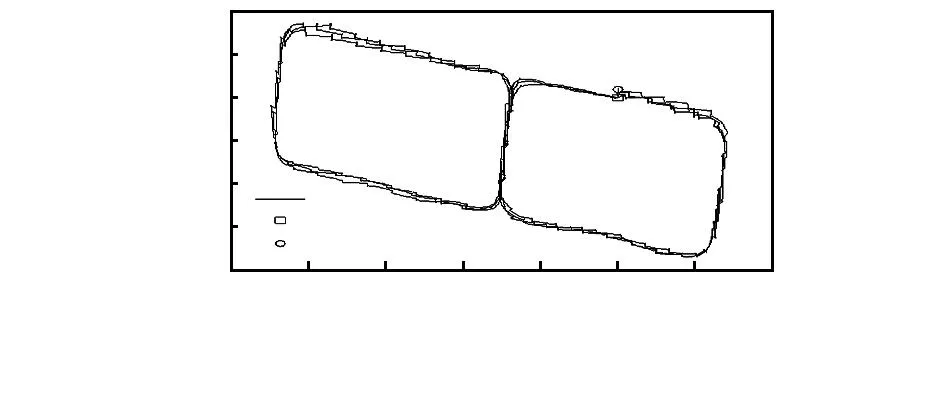
图9　行进轨迹显示Fig 9　March trajectory display

实验中的行走路径为两个约为13.5 m×6.8 m的矩形，共行走3圈，行走距离为243.6 m，由图中轨迹显示结果可以看出:三条轨迹基本重合，验证了算法的稳定性。起落点的误差距离为1.78 m，因此,其定位精度误差为整个行走距离的0.73 %。

5结论

本文依据行人的步行运动特征将每一步按照脚的运动状态划分为4个隐马尔可夫隐含状态，以单轴的角速度数据为观测量，同时利用Baum—Welch算法训练和优化模型参数，从而实现了运动过程中的零速区间的有效检测。实验结果表明:该方法能够有效地检测出行人步行运动过程中的零速区间，且采用该方法进行零速检测的行人惯性导航系统的稳定性较好，其定位误差在整个行走路程的1 %以内。

参考文献:

[1]Foxlin E.Pedestrian tracking with shoe-mounted inertial sensor-s[J].Computer Graphics and Applications,IEEE,2005,25(6):38-46.

[2]崔潇,秦永元,周琪,等.鞋式个人导航系统算法和试验研究[J].测控技术,2013(3):138-142.

[3]李超,苏中,朱嘉林.可穿戴式自主定位技术的零速触发算法研究[J].传感技术学报,2014,27(5):627-632.

[4]Skog I,Händel P,Nilsson J O,et al.Zero-velocity detection—An algorithm evaluation[J].IEEE Transactions on Biomedical Engineering,2010,57(11):2657-2666.

[5]Cheshomi S,Rahati Q S,Akbarzadeh T M R.Hybrid of chaos optimization and Baum-Welch algorithms for HMM training in continuous speech recognition[C]∥2010 International Conference on Intelligent Control and Information Processing(ICICIP),IEEE,2010:83-87.

[6]ParkSK,SuhYS.Azerovelocitydetectionalgorithmusinginertialsensorsforpedestriannavigationsystems[J].Sensors,2010,10(10):9163-9178.

Zero velocity detection algorithm for pedestrian inertial navigation*

FEI Cheng-yu, SU Zhong, LI Qing

(Beijing Key Laboratory of High Dynamic Navigation Technology,University of Beijing Information Science & Technology,Beijing 100101,China)

Abstract:In pedestrian inertial navigation, zero velocity detection is premise to reset velocity errors and estimate navigation error.Aiming at problem that time interval of zero velocity is short and it is difficult to detect in pedestrian moving process,a zero velocity detection algorithm based on human foot movement characteristics is proposed,where walking motion is abstracted into a hidden Markov model with 4 hidden states and 15 observations, and construction mechanism of model is described.The model parameters are trained and optimized by Baum—Welch algorithm and detection accuracy is improved.Experimental results show that the proposed method has better effect on zero velocity detection, and the positioning error of pedestrian inertial navigation system using this method is about 0.73 % of the travel distance, and the positioning precision is high.

Key words:pedestrian inertial navigation; zero velocity detection; hidden Markov model; Baum—Welch algorithm

DOI:10.13873/J.1000—9787(2016)03—0147—04

收稿日期：2015—07—09

*基金项目：国家自然科学基金资助项目(61471046)；北京市科技计划课题项目(Z131100005313009)；北京市教委创新能力提升计划项目(PXM2015—014224—000029)

中图分类号：TP 212.9

文献标识码：A

文章编号：1000—9787(2016)03—0147—04

作者简介:

费程羽(1991-)，男，吉林省长春人，硕士研究生，研究方向为惯性器件和惯性导航系统。