接触式扫描过程中探针—样品赫兹耦合的建模与分析*

陈　伟， 许　斌， 赵世平

(四川大学 制造科学与工程学院，四川 成都 610065)



接触式扫描过程中探针
—样品赫兹耦合的建模与分析*

陈伟， 许斌， 赵世平

(四川大学 制造科学与工程学院，四川 成都 610065)

摘要:随着微器件测量系统中微测头尺寸不断减小和测量精度不断提高，微纳测量中测头—样品间的形变误差对系统不确定度的影响是不能忽略的。为了研究二者间的相互作用和形变问题，根据材料应力—应变属性和赫兹理论，建立了微测球与样品的接触模型，并以玻璃测头和光学器件为分析对象，探讨了测量力、测球半径、样品曲率半径以及不同材质样品等对形变、形变区域半宽长度及最大赫兹应力的影响。结果表明：测球半径与样品曲率半径的作用机理相似，而且相较于探针测球半径因素，测量力和被测样品不同曲率半径因素对探针—样品间形变的影响更为显著。

关键词：接触式扫描; 赫兹理论; 测量力; 测球半径; 测量误差

0引言

随着精密微细加工技术和先进制造业的快速发展，各种复杂新型微结构不断出现，微结构表面形貌接触式测量以触针式测量最为常见[1,2]。对于接触式位移传感器，探头与样品间的赫兹耦合和形变将直接影响测量结果的不确定度，二者耦合作用越强，形变就越大，测量精度越低。影响耦合和形变的因素主要有测量力、探头半径、样品曲率半径和样品的弹性模量。Yan Wenyi[3,4]研究了测球—样品间的相互作用，并通过仿真探究了形变与最大应力的关系。Jin Fan[5]，Terekhina S[6]，Palade A C[7]通过球面模型研究了形变量、半宽长度、测量力间的相互关系及接触区域赫兹应力的分布。传感器测量力往往是通过测量结果与标准样品的比对或借助力传感器进行标定，而并未从测球—样品形变导致测量差角度来进行研究[8]。李志渤、黄强先等人[9]针对三坐标测量机(coordinate measurement machine,CMM)测头问题，研究了不同材质测球对不同样品所需的最大测量力，在测力为10 mN时计算了测球—样品的形变量，但CMM的测头直径通常为mm级，这并不适用于复杂微结构测量。杨盛福等人[10]通仿真验证了ANSYS仿真解和赫兹解的一致性，冯剑军等人[11]研究了圆柱—平面间的滑动接触，仿真中加入摩擦因素，研究了赫兹应力在接触面上的分布。

本文基于材料的应力—应变属性和经典赫兹接触理论，分析了测头—样品间的相互作用，建立了相应数学模型，并以玻璃测头和玻璃光学样品器件为分析对象，探讨了测量力、测球半径、样品曲率半径以及不同材质的被测样品等因素对探针—样品间的形变、形变区域半宽长度及最大赫兹应力的影响。

1测头—样品间的赫兹耦合模型

每一种材料都有其固有的应力—应变曲线如图1所示，横坐标ε为应变量，纵坐标σ为应力值，这是材料的固有属性，由材料自身性质决定[12]。在弹性形变阶段应力—应变近似线性关系,即σ=Eε，式中E为材料弹性模量。当应力超过E's点(弹性极限点)，应力—应变呈非线性关系，材料发生塑性形变。接触式测量过程当测量力小于弹性极限σe，材料发生弹性形变，当测量力大于σe，材料发生塑性形变即为有损测量。为了保证整个测量过程中实现无损检测，通常要求最大测量力应小于σe。

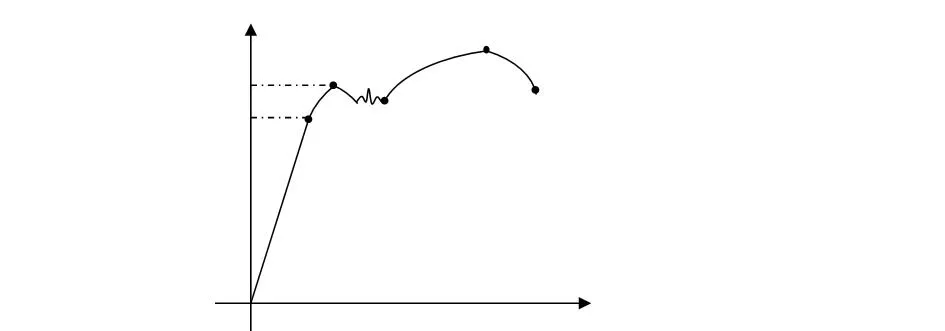
图1　材料的应力—应变特征曲线[12]Fig 1　Stress-strain characteristic curve of materials[12]

由于加工技术和加工方法的缺陷，加工工件表面通常存在着随机分布且大小不等的凸峰和凹谷(以凸峰为主)[13]。形貌测量过程中测头先与微凸峰相接触，如图2(a)所示。测头—样品间的接触就是微凸峰间的接触，测头—样品间的相互作用就是微凸峰间的相互作用。被测样品表面粗糙度的形状通常是椭圆体，因其接触区域尺寸远小于探头和被测工件本身的曲率半径，因此粗糙度可以近似为球体[14]。因此，“测头—样品”的接触问题可以视为一系列高低不齐的“球体—球体”接触，具体接触模型如图2(b)和图2(c)所示。

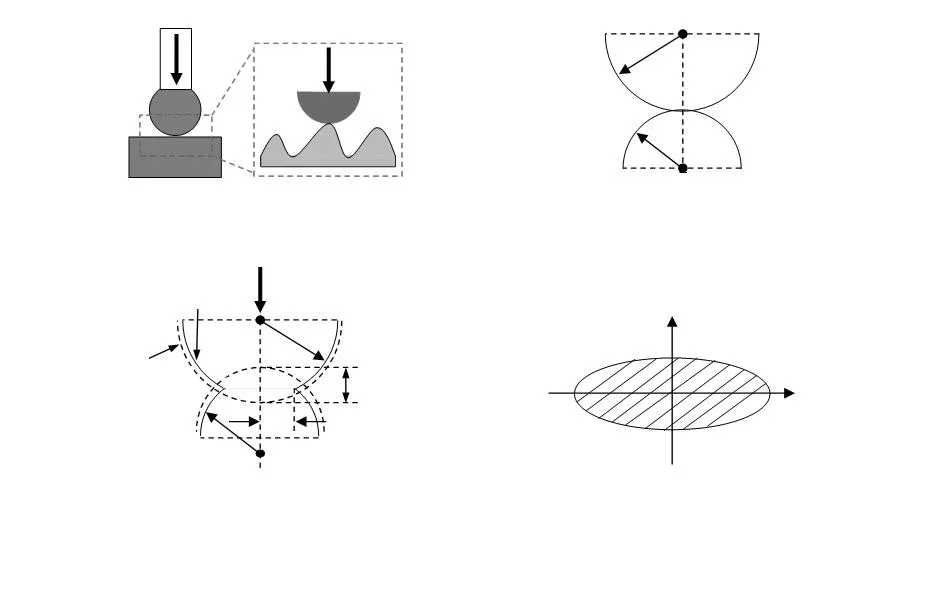
图2　测球—样品凸峰接触时的形变示意图[14]Fig 2　Deformation diagram of peak contact of probe-sample[14]

由经典赫兹接触理论[15]可知，当测量力F作用于Z轴，在接触点附近发生局部形变并形成一个较小的椭圆形接触面，长半轴在X轴上，短半轴在Y轴上如图2(d)所示。椭圆形接触面上各点单位压力大小与材料的形变量有关，沿Z轴将产生最大单位压力。

接触区域沿Z轴的最大形变量δ为

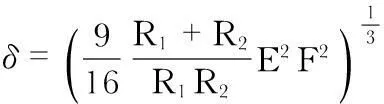
(1)

形变区域椭圆长轴半轴宽度a为

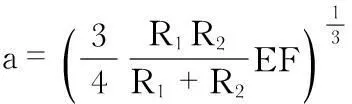
(2)

最大赫兹应力应出现在形变量最大处，最大赫兹应力Qmax为

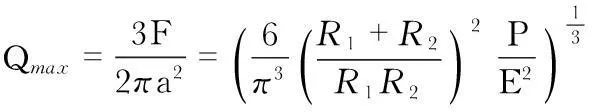
(3)

当被测样品为刚性材质时，求解过程中只需将式(1)、式(2)、式(3)中R2换成+∞；当探针与凹体接触时R2变为-R2。

2形变因素分析

微结构测量中，精密微位移传感器测量力F通常为零点几毫牛至数毫牛，本文选取F<1mN；微探针半径R1和样品曲率半径R2为数微米。

2.1测量力对形变的影响

接触式微位移传感器的测量力是影响测量精度重要因素之一，测量力的大小将直接决定着微结构形貌检测质量的高低，前文已有论述。测头—样品间形变量因测量力的不同而不同。测量力对测头—样品间的形变量、形变区域长轴半宽长度、最大赫兹应力的影响如图3所示。实线表示形变量与测量力的关系，点画线表示半宽长度与测量力的关系，虚线表示最大赫兹应力与测量力的关系。由图可知，测头—样品间的形变量与测量力呈正相关，随着测量力的增大，形变量不断变大。当测量力F为1mN时，被测样品曲率半径R2为1μm，测球半径R1为5μm时，沿测量力方向最大形变量为1.04μm，长轴半宽长度为29.4μm，而最大形变处的最大赫兹应力为552N/mm2。在测量过程中应根据形变误差允许范围，选取恰当稳定的测量力，保证测量的精度和可靠性。

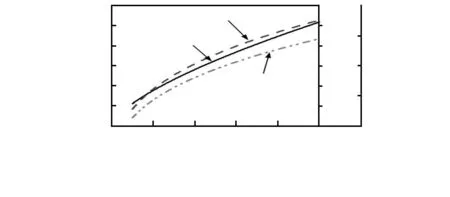
图3　测量力对形变量、半宽长度、最大赫兹应力的影响Fig 3　Influence of measurement force on deformation quantity,half-width length and the maximum Hertz stress

2.2微探头半径对形变的影响

探针测球半径对测头—样品间的形变量、形变区域长轴半宽长度、最大赫兹应力的影响如图4所示。实线表示形变量与测球半径的关系，点画线表示半宽长度与测球半径的关系，虚线表示最大赫兹应力与测球半径的关系。测球半径与测头—样品间的形变量呈负相关，随着探头半径的增大，形变量不断减小。测球半径与长轴半宽长度呈正相关，随着探头半径的增大，长轴半宽长度随之增加。最大赫兹应力与形变量呈正相关，亦即与测球半径呈正相关。但同时也应注意到，测球半径的增加，对于复杂微结构形貌的测量必然会增加某些测量盲区，所以,不能为了减小测头—样品间形变量而盲目地增大测球半径。

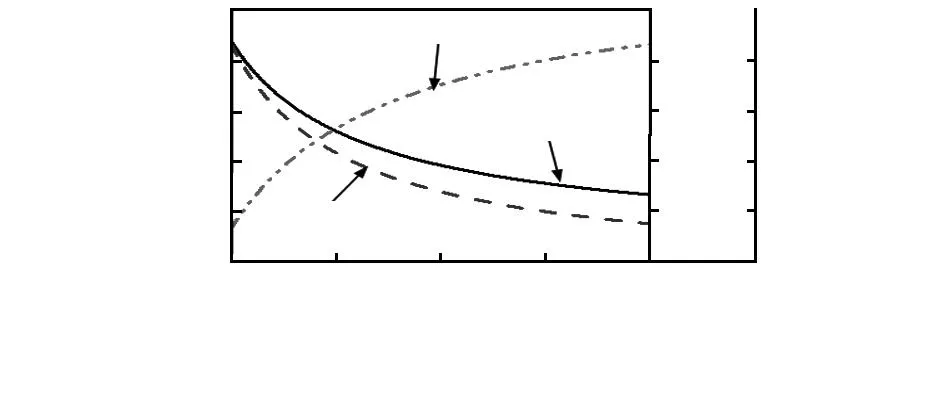
图4　测球半径对形变量、半宽长度、最大赫兹应力的影响Fig 4　Influence of probe radius on deformation quantity,half-width length and the maximum Hertz stress

2.3样品曲率半径对形变的影响

在整个测量过程中，随着样品不同位置曲率半径的不同而需要不同的测量力，在整个动态测量过程中需要不停地改变测量力的大小，以便实现最可靠的测量。工件不同位置的曲率半径对测头—样品间的形变量、形变区域长轴半宽长度、最大赫兹应力的影响如图5所示。实线表示形变量与样品曲率半径的关系，点画线表示半宽长度与样品曲率半径的关系，虚线表示最大赫兹应力与样品曲率半径的关系。由图可知，随着被测样品曲率半径的增加探针—样品间的形变量逐渐减小，这是因为曲率半径的增加使得测头和样品间的接触面积增加，二者表面抵抗形变的能力增强。最大赫兹应力与形变量呈正相关，当形变量随着被测样品曲率半径的增加而减小时，最大赫兹应力也相应地减小。工件不同位置的曲率半径对形变量、半宽长度的作用机理与探针测球半径相似，所以,二者对测头—样品间的形变量、形变区域长轴半宽长度、最大赫兹应力的影响和趋势大致相同。

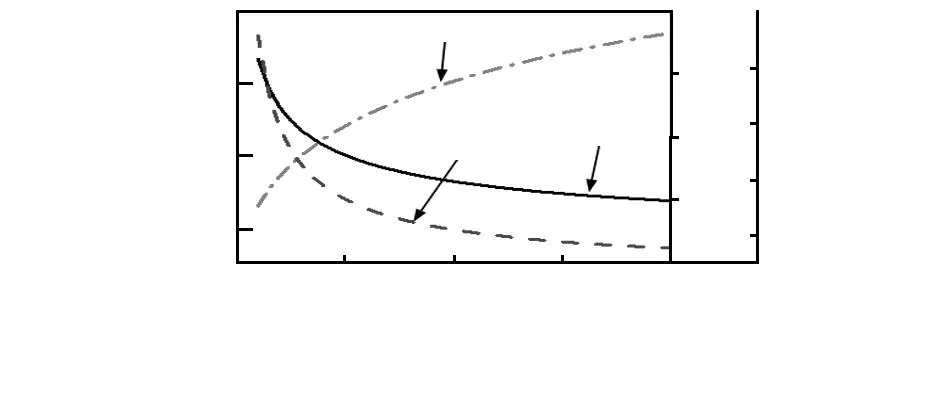
图5　工件曲率半径对形变量、半宽长度、最大赫兹应力的影响Fig 5　Influence of sample radius on deformation quantity,half-width length and the maximum Hertz stress

2.4不同材质弹性模量对形变的影响

本文选取了几种不同材质的被测样品如表1所示，用于研究不同材质的弹性模量对于探针—样品间的形变量、形变区域长轴半宽长度、最大赫兹应力的影响。

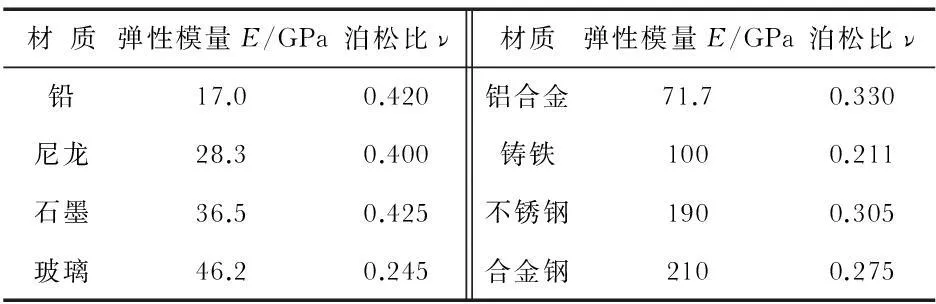
表1　不同材质的被测样品参数表

被测样品材质弹性模量对测头—样品间的形变量、形变区域长轴半宽长度、最大赫兹应力的影响如图6所示。由图可知，随着被测样品材质弹性模量的增加，测头—样品间形变量和形变区域的半宽长度都逐渐减小，二者趋势基本一致。当弹性模量小于1.5 GPa，测量力F=0.5 mN，测球半径R1=5 μm，工件曲率半径R2=1 μm时，测球—样品间形变量最小为0.5 μm。实际测量中应根据不同材质的被测样品选取合适的测量力。如当被测样品为柔性材质时，应选取更小的测量力，以减小测头—样品间形变对测量结果的影响；当被测样品的弹性模量较大时，可以选取较大的测量力，以保证测量过程中测头—样品充分稳定接触。

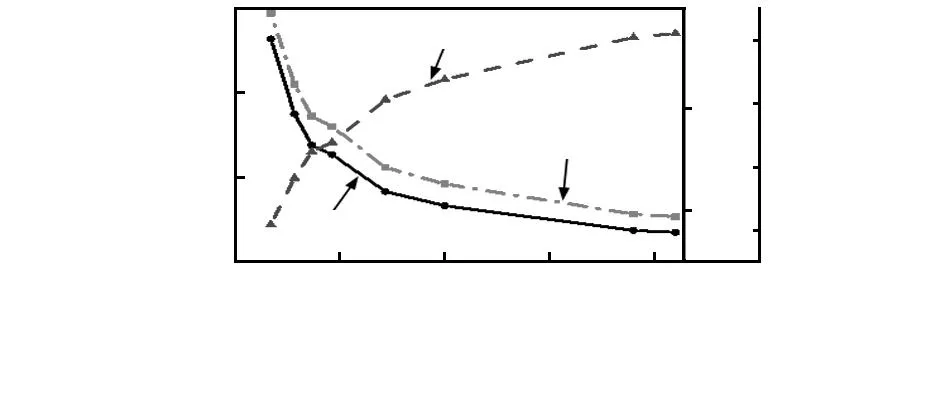
图6　工件弹性模量对形变量、半宽长度、最大赫兹应力的影响Fig 6　Influence of workpiece elastic modulus on deformation quantity,half-width length and the maximum Hertz stress

3结论

本文针对探针测头—样品间的赫兹耦合和形变问题，基于材料的应力—应变属性和经典赫兹接触理论，分析了探针测头与被测样品间的相互作用，建立了相应数学模型，并以玻璃测头和玻璃光学样品器件为分析对象，着重探讨了测量力、测球半径、被测样品不同曲率半径以及不同材质的被测样品等因素对探针—样品间的形变、形变区域半宽长度、最大赫兹应力的影响，分析其内在作用原理，寻找最大的影响因素。通过仿真分析可以看出：测球半径与样品曲率半径的作用机理相似，而且相较于探针测球半径因素而言，测量力和被测样品不同位置曲率半径因素对探针—样品间形变的影响更为显著。针对不同材质的被测样品，应选取恰当的测量力和测头半径，以保证最佳的测量效果。

参考文献:

[1]中国科学院.中国学科发展战略:微纳电子学[M].北京:科学出版社,2013.

[2]王伯雄,陈非凡,董瑛.微纳米测量技术[M].北京:清华大学出版社,2006.

[3]Yan W,Sun Q,Feng X Q,et al.Analysis of spherical indentation of superelastic shape memory alloys[J].International Journal of Solids and Structures,2007,44(1):1-17.

[4]Yan W,Sun Q,Liu H Y.Spherical indentation hardness of shape memory alloys[J].Materials Science and Engineering:A,2006,425(1/2):278-285.

[5]Jin F,Zhang W,Zhang S,et al.Adhesion between elastic cylinders based on the double-Hertz model[J].International Journal of Solids and Structures,2014,51(14):2706-2712.

[6]Terekhina S,Fouvry S,Salvia M,et al.An indirect method based on fretting tests to characterize the elastic properties of materials:Application to an epoxy resin RTM6 under variable temperature conditions[J].Wear,2010,269(7/8):632-637.

[7]Palade A C,Pillon G P,Cicala E,et al.Subsurface treatment of a contact subjected to a Hertz pressure[J].International Journal of Mechanical Sciences,2013,77:107-112.

[8]王海涛,林玉池,付鲁华，等.微小力测量系统的实验研究[J].传感器与微系统,2009,28(11):8-11.

[9]李志渤,黄强先,赵剑,等.接触测量中的微探球力变形研究[J].中国机械工程,2014,24(14):1926-1929.

[10] 杨盛福,陈锦江,刘坤.ANSYS在弹性体点接触分析中的应用[J].机械研究与应用,2007,20(4):107-108.

[11] 冯剑军,谭援强.基于Hertz理论圆柱和平面之间的滑动接触分析[J].摩擦学学报,2009,29(4):346-350.

[12] 郑修麟.材料的力学性能[M].西安:西北工业大学出版社，2011.

[13] 付移风,潘晓彬,陈福练.便携式表面粗糙度测量仪的设计[J].传感器与微系统,2010,29(2):93-97.

[14] 田红亮，朱大林，方子帆.两弹塑性接触粗糙表面的严格解析解[J].机械设计与制造,2010，32(1):225-227.

Modeling and analysis of probe-sample Hertz coupling in contact scanning*

CHEN Wei, XU Bin, ZHAO Shi-ping

(School of Manufacturing Science and Engineering,Sichuan University,Chengdu 610065,China)

Abstract:As the size of probe used for micro-component measurement system is decreased continuously and measurement precision is increased constantly,influence of deformation error between probe and measurement sample on uncertainty of system is becoming an issue that can not be ignored.In order to research interaction between probe and sample and deformation problems,contact model for micro measuring ball and sample is established according to stress-strain properties of materials and Hertz theory,glass probe and optical devices are used as analysis target,effect of measurement force,probe radius,curvature radius of sample and samples with different materials on deformation,half width length of deformation zone and the maximum Hertz stress.Results show that interaction mechanism of curvature radius of measured sample and measuring ball radius is similar, and compared with probe radius factor,effect of measurement force and curvature radius factor of measured sample on deformation between probe and ample is more obvious.

Key words:contact scanning; Hertz theory; measurement force; probe radius; measurement error

DOI:10.13873/J.1000—9787(2016)03—0012—04

收稿日期：2016—01—18

*基金项目：国家自然科学基金资助项目(51405314)；中国物理研究院超精密加工技术重点实验室开放基金资助项目(KF15004)；中央高校基本科研业务费资助项目(2015SCU04A12)

中图分类号：TH 711

文献标识码：A

文章编号：1000—9787(2016)03—0012—04

作者简介:

陈伟(1989-)，男，四川遂宁人，硕士研究生，主要研究方向为微形貌测量、传感器设计及不确定度分析。

许斌，通讯作者，E—mail:bin_xu@scu.edu.cn。