基于多智能体遗传算法的战术航段优化
2016-06-13饶卫平杨任农雷晓义柴毅哲
饶卫平, 杨任农, 雷晓义, 柴毅哲
(空军工程大学 航空航天工程学院,陕西 西安 710038)
基于多智能体遗传算法的战术航段优化
饶卫平, 杨任农, 雷晓义, 柴毅哲
(空军工程大学 航空航天工程学院,陕西 西安 710038)
摘要:针对飞机战术飞行要求和威胁规避目标的问题,采用优势函数和战术规避相结合的原则,将战术航段优化问题转化为路径搜索问题,提出了基于多智能体遗传算法来解决此问题。采用自适应交叉和变异算子,改进自学习算子获取子代的算法,实现了全局最优的结果。通过和传统遗传算法进行仿真比较,相比之下,基于多智能体的遗传算法可以有效利用地形,实现战术飞行。
关键词:战术优化; 多智能体; 遗传算法
0引言
飞机战术飞行是飞机空战和突防的重要内容。突防中的战术飞行动作,是根据实时的飞行环境,在飞行员的判断和战术决策下,做出的符合战术任务的动作,这些动作将使飞机尽可能处于自我保护状态下,从而发射武器,打击目标,以此来提高作战能力的目的。
在飞行中,需要对战术动作进行一定的决策,而这些决策动作是根据机动动作库组合起来实现的,然后,基于这些战术动作根据战场环境对战术进行优化。战术优化的基本思想是建立优化目标函数,利用机动动作库,采用某种优化方法,在一定的约束限制情况下寻求最佳的优化设计。战术优化设计需满足以下几个特点:1)限制较多:由于突防情况所考虑的条件众多,既要考虑飞机飞行要求,又要考虑战场地形条件,还要规避威胁,使得优化过程约束条件众多。2)优化评价函数必须满足飞机速度、飞行高度、战术动作,先进武器的发射以及规避威胁等因素。3)战场环境复杂,对数据模型的建立比较困难。战场环境瞬息万变,敌人雷达火炮的不可预知,这些都加大了模型建立的难度[1]。
国内外对战术优化的方法已进行了大量的研究,如Voronoi图法[2]、A*搜索法、微分进化法等。这些方法在解决复杂非线性战术优化问题上存在着一定的局限性,如无法得到最优解、运算量巨大等。但是遗传算法因其自身隐含的并行性和多目标优化特点,适合于复杂、非线性的优化问题,因而,受到越来越多的学者研究。由于传统的遗传算法具有初始种群随机生成的特性,在进化过程中容易陷入局部最优,因此,本文引入多智能体技术,采用自适应的交叉变异算子,将多智能体的优点和遗传算法的优点结合,从而有效地解决了飞行战术优化的问题。
1战术优化问题的数学描述
对战术航段的优化是一个典型的多目标优化问题。为了评价一段战术航段的好坏应该从战术要求、飞行状态、环境条件进行详细分析以此来判断是否达到飞行器的最佳飞行指标和是否达到最佳的战术意图。飞行指标由飞行评价函数fRoute表示,其意义是战斗机作为飞行器的一类,即战斗机具有飞行属性,这就需要其在飞行过程中尽可能达到距离约束Dr和高度约束Hr,以减少对装备的损耗以及飞行中的油耗;战术指标执行的好坏则可以由战术评价函数ftactic表示,其意义是战斗机作为战斗单元的一类,即战斗机具有战斗属性,这就需要其在飞行过程中尽可能达到战术指标,由攻击条件决定,包括在敌目标区飞行时间tfly尽可能短,飞行高度hfly尽可能低,被敌威胁源探测的概率fthreat尽可能小,以及被锁定时需进行尽可能剧烈的机动elock。
其中,Dr为飞行航路的限制约束,则其可以表示为
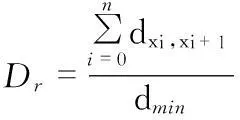
(1)
式中dxi,xi-1为航迹点xi到xi+1的距离,dmin为开始规划点到目标点的直线距离。
飞行高度Hr的设置是为了更好地跟随地形飞行,提高掩护效果[3],其表达为
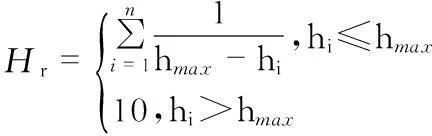
(2)
式中hi为战术航段点i高度,hmax为飞行最大高度。
以雷达或导弹为中心,其周边处于不同的位置的点所感知的信息是不同,这些信息将影响飞机所受到的威胁程度,其信息感知范围可以分为四类:通信范围RC,侦察范围RS,作战范围RT,行动范围RM,如图1所示,显然有RC>RS>RT>RM[4]。这些感知范围对于飞机的威胁也是不同的,其构成了一个多环的威胁模型,飞机处于不同的“环”其所受威胁程度是不一样的,在同一环内其威胁值可以简单地认为只与飞机与威胁源的距离成比例,那么被敌探测概率可以表示为式(3)
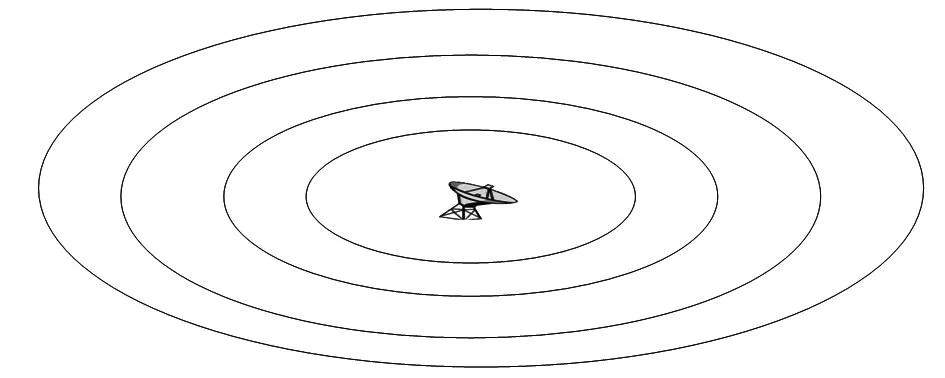
图1 信息感知多环示意图Fig 1 Diagram of multi-cyclic of information perception
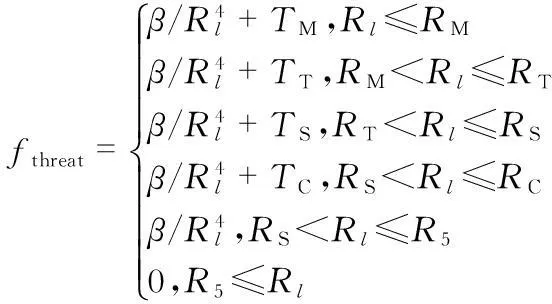
(3)
式中TM,TT,TS,TC分别为飞机进入RM,RT,TS与RC环的惩罚值,显然有TM>TT>TS>TC,Rl为飞机到威胁源的水平距离,R5为飞机可被威胁的最大距离。
机动剧烈程度评价函数elock与飞机机动时过载的变化率有关,但是剧烈的机动不能有太大的速度v,一般不高于0.7MH,即约等于210m/s,那么在某一区域的停留时间Δti必然大于以最大速度通过的时间ti min=li/vi max,且剧烈的机动通常会带来航段长度l的增加与飞行高度hi的损失,可见两个目标是互相冲突的。对于规避防空导弹来说,一般可以得到elock的数学表达式为
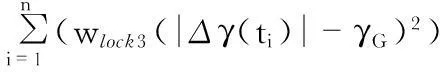
(4)
即在某一时刻飞机的控制量变化越剧烈就认为其更可能不被锁定或更容易脱锁,其中wlock1,wlock2与wlock3为加权系数,根据具体机动的情况而定,与基本机动动作相对应。通过以上分析,已经可以给出此多目标优化问题的数学描述,其中一个目标是我方战机的飞行代价froute(x)最小,另一个目标是战机的战术代价floxk(x)最小,如式(5)
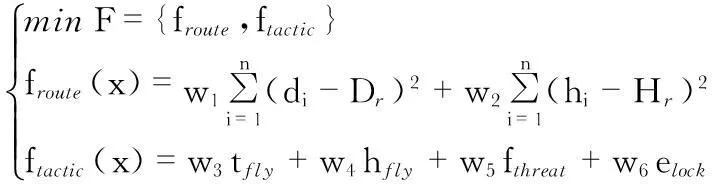
(5)
就躲避防空导弹攻击而言,需要考虑借助地形进行规避,那么高度指标可以放宽些,即w2可以设置的小一些。具体的加权系数应根据上级指挥信息系统给出的具体任务的交战规则得出,仿真一般按照:首先保存自己、其次完成任务的逻辑对加权系数做以限定,即系数w5,w6最高,下来是w3,w4两个参数,而w1,w2最小。
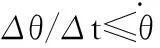
2多智能体遗传算法求解战术优化问题
智能体是物理或者虚拟的实体,具有自治性、反应性、主动性和适应性等特点,因此,可以描述多变复杂的环境[5]。由若干智能体为了相同的目的而相互协同作用形成的计算系统就构成了多智能体系统。将战场环境转换为三维网格,由网格点所组成的一个战术航路代表一个智能体,这样不同的战术航路所组成的集合就构成了智能体网格,记为L,网格的大小为Lsize×Lsize,其中,Lsize为整数。每个智能体固定在一个格子点上,则第i行、第j列的智能体为Li,j,i,j=1,2,…,Lsize,每个智能体不能移动,只能和邻域发生作用。
智能体网格如图2所示,每个圆圈表示一个智能体,圈中的数字表示该智能体在网格中的位置,而有连线的两个智能体才能发生相互作用[6]。
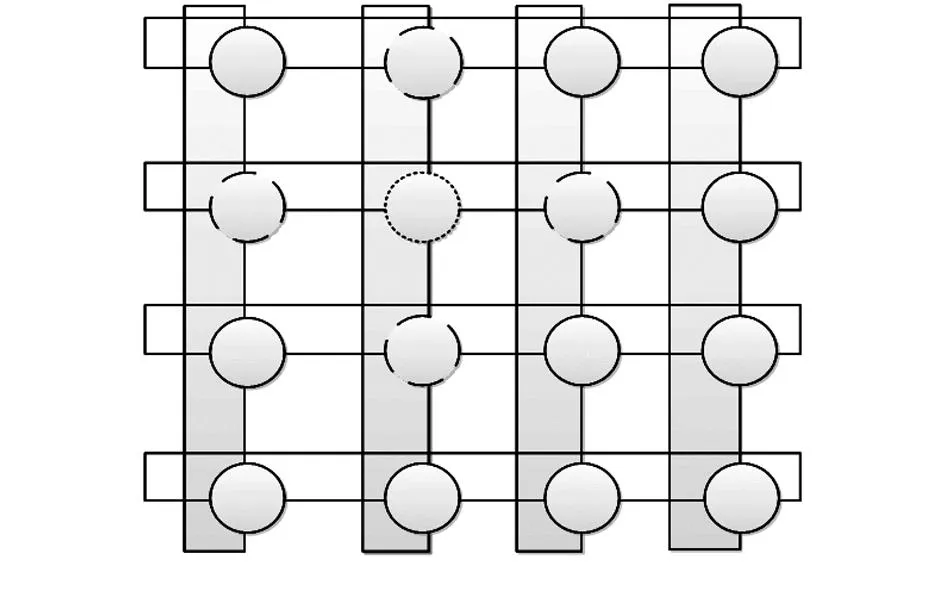
图2 智能体网格Fig 2 Agent lattice
基于以上定义,给出具体算法过程如下:
1)初始化基因编码
定义待优化的有效段为一个染色体(即一个个体),一个基因即为该段中的一个仿真点,可表示为Wi=〈xi,yi,zi,Vi,θi,ψi〉,且优化航段起始点和终止点的状态是不变的,那么其可行解为
X=[x1,y1,z1,V1,θ1,ψ1,…,xn,yn,zn,Vn,θn,ψn].
(6)
若设种群规模为N,则解的空间为
Xi=[xi1,yi1,zi1,Vi1,θi1,ψi1,…,xin,yin,zin,Vin,θin,
ψin],i=1,2,…,N.
(7)
2)初始化种群
由所有的基因编码组成的一个可行解组成的集合就是初始化种群的一个个体,表示为X0=[x01,y01,z01,V01,θ01,ψ01,…,x0n,y0n,z0n,V0n,θ0n,ψ0n],假设种群规模为100,则可将这些种群作为由100个智能体所组成的多智能体网格,对多智能体进行遗传操作。
3)变异(mutation)
首先根据式(8)产生一个新的智能体muti,j=(e1,e2,ek…,en),其中
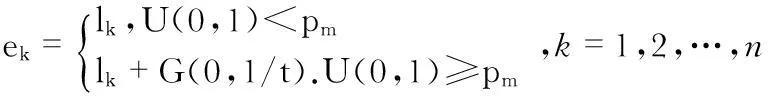
(8)
其中,G(0,1/t)为高斯分布的随机数,t为进化的代数。然后用这个新生成的Muti,j来代替Li,j。这种变异算子采用了高斯变异算子,所以,只在Li,j上的某些分量上叠加了一个小的扰动。而pm可由下列函数表示为
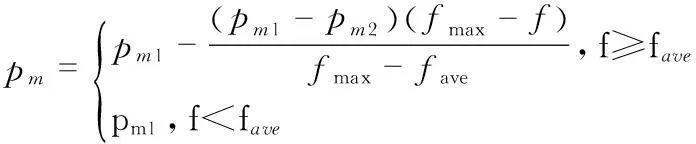
(9)
式中f为变异个体的适应度值,而pm1和pm2分别为设定好的最大和最小的变异概率。利用这个式子可以达到自适应性的目的[7]。
4)交叉(crossover)
将变异后的个体Muti,j=(e1,e2,…,en)与目标个体Xi,j=(x1,x2,…,xn)进行杂交来产生新的个体Croi,j=(c1,c2,…,cn),这里使用二元交叉
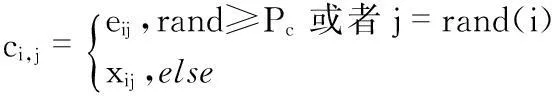
(10)
其中,rand是[0,1]之间的随机数,j=rand(i)使得至少会有一个基因发生变化,保证了每次交叉都会有新个体产生。这里的Pc可以采用具有自适应功能的交叉算子[7]
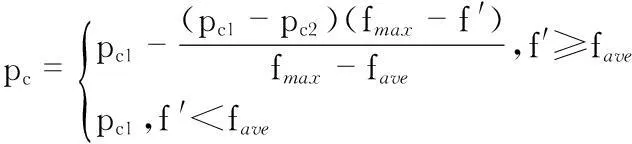
(11)
式中f ′为需要交叉个体的适应度值,fmax和fave为种群的最大适应度和平均适应度值,而pc1和pc2分别为设定好的最大和最小的交叉概率。
5)选择(selection)
接着对Croi进行适应度评价,若满足式(12),则在下一代中用Croi替换Xi
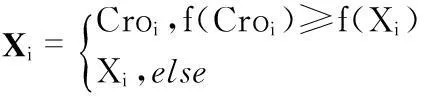
(12)
其中,f(x)=froute(x)+ftactic(x),这里规定每产生一个Croi个体即马上进行选择,并参与后续的进化过程。
6)自学习
智能体可以通过自学习来提高求解能力,这里根据Li,j的信息构建一个小规模的多智能体遗传算法[8]。在自学习算子中,首先需要生成一个智能体的网格,这里用SL表示,其大小定义为sLsize×sLsize,其上的所有智能体表示为sLi′,j′,i′,j′=1,2,…,sLsize,其由式(13)产生
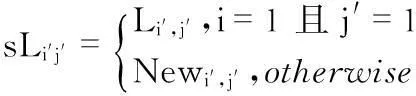
(13)
在这里的Newi′,j′=(ei′,j′,1,ei′,j′,2,…,ei′,j′,n),而其中根据式(14)产生
ei′j′k=
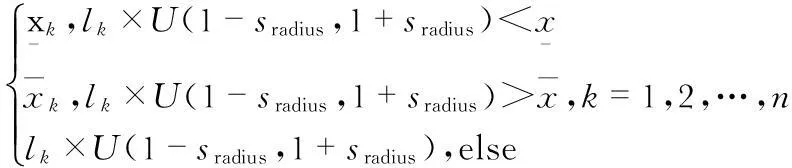
(14)
这里面的sradius∈[0,1]表示搜索的半径。由上面所产生的智能体经过变异、交叉,之后和上面的目标智能体进行比较,选出适应度最高的个体代替本代的最终智能体。
7)循环迭代
遍历所有的种群,并进行循环迭代,直到满足最大迭代次数结束。整个操作的流程如图3所示。

图3 多智能体遗传算法流程图Fig 3 Flow chart of multi-agent genetic algorithm
3仿真验证
参数设置如下:wlock1=0.4,nxG=2,wlock2=0.3,nyG=6,wlock3=0.3,γG=π/4;加权系数w1=0.2,w2=0.2,w3=0.4,w4=0.4,w5=0.6,w6=0.6,在使用多智能体遗传算法时所设置的仿真参数为:Lsize=10,pc1=0.4,pc2=0.7,pm1=0.01,pm2=0.05,sLsize=4,sradius=0.2得到仿真结果如图4与图5,仿真总用时124s。

图4 优化结果局部放大后的三维效果图Fig 4 3D effect picture of amplifying optimized result
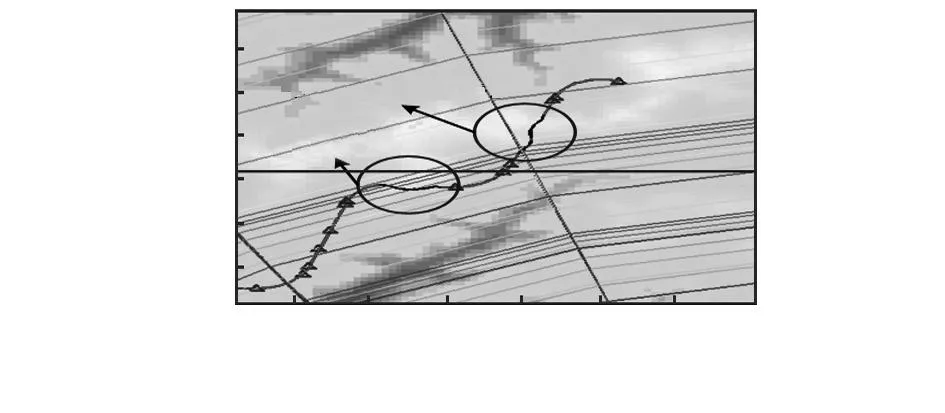
图5 优化结果俯视图Fig 5 Top view of optimized result
图5圆圈中标示出的两条黑色线条即经过多智能体遗传算法优化出的战术轨迹,分别记为优化后的战术轨迹段1和优化后的战术轨迹段2,可以看出:轨迹段考虑了一定的地形因素并做出了一定的战术机动,为了更清楚地观察优化结果,将使用多智能体遗传算法优化和普通遗传算法的结果放在一起进行比较如图6所示。
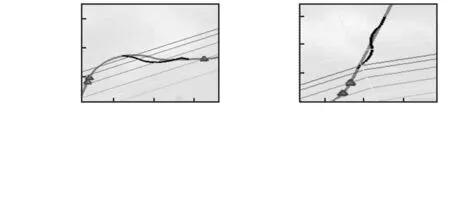
图6 多智能体遗传算法和普通遗传算法对战术轨迹段1与战术轨迹段2优化俯视对比图Fig 6 Topview comparison of optimization of tactical route 1and tactical route 2 using multi-agent genetic algorithm andtraditional genetic algorithm
图6(a)为通过多智能体遗传算法和普通遗传算法对战术轨迹段1优化俯视对比图,图6(b)为通过这两种方法对战术轨迹段2优化的俯视对比图,其中黑色线条为多智能体遗传算法所优化的不同部分,灰色为普通话遗传算法所优化的情况,从中可以清晰地看出多智能体遗传算法优化的轨迹(黑色表示)对地形有较明显的回避,且曲线较为平滑,结果较为满意。
4结论
本文将多智能体改进的遗传算法引进到突防战术优化中,建立了合适的评价函数,尤其是对威胁进行分环分析,使用网格形式存储智能体,并对遗传算法进行自适应的交叉因子和变异因子改进,极大改进了传统遗传算法容易陷入局部收敛的情况。通过引进多智能体系统,尤其是自学习算子,有效地将自学习自适应的特点体现出来。仿真结果显示:此算法有效优化战术航段,具有很好的实用价值。
参考文献:
[1]周德云,李峰,蒲小勃,等.基于遗传算法的飞机战术飞行动作决策[J].西北工业大学学报,2002,20(1):109-112.
[2]McLainTW,ChandlePR,RasmussenS,etal.CooperativecontrolofUAVrendezvous[C]∥Proceedingsofthe2001AmericanControlConference,2001:2309-2314.
[3]巴海涛.无人机航迹规划研究[D].西安:西北工业大学,2006.
[4]刘胜.基于Agent的机动通信战术规划的研究[D].杭州:浙江大学,2006.
[5]余斌.Multi-Agent 研究与应用[D].合肥:安徽大学,2006.
[6]Peng Zhihong,Wu Jinping,Chen Jie.Three-dimensional multi-constraint route planning of unmanned aerial vehicle low-altitude penetration based on coevolutionary multi-agent genetic algorith-m[J].Journal of Central South University of Technology,2011,18(5):1502-1508.
[7]王健.基于遗传算法的无人机飞行器航迹规划研究与实现[D].长沙:国防科技大学,2011.
[8]饶卫平,杨任农,雷晓义,等. 基于多智能体遗传算法的无人机突防航线规划[J].计算机仿真,2015,32(4):39-43.
Tactical optimization based on multi-agent genetic algorithm
RAO Wei-ping, YANG Ren-nong, LEI Xiao-yi, CHAI Yi-zhe
(College of Aeronautics and Astronautics Engineering,Air Force Engineering University,Xi’an 710038,China)
Abstract:Aiming at demand of tactical flight and problem of threating avoidance target in airplane route planning,using principle combining advantage function with tactics avoidance,tactical segment optimization problem is turned into path searching issue,propose a tactical segment optimization method based on multi-agent genetic algorithm.By adopting self-adaptive crossing and mutation operator, improve algorithm which acquirs next-generation by self-learning operator ,achieve global optimal result.Simulation results show that compared with traditional ones the improved genetic algorithm can effectively use terrain to fulfill tactical flight tasks.
Key words:tactical optimization; multi-agent; genetic algorithm
DOI:10.13873/J.1000—9787(2016)03—0040—04
收稿日期:2015—07—16
中图分类号:TP 18
文献标识码:A
文章编号:1000—9787(2016)03—0040—04
作者简介:
饶卫平(1990-),男,陕西商洛人,硕士研究生,主要研究领域为任务规划。
杨任农,通讯作者,E—mail:857805523@qq.com。
