左右极限定理适用范围的应用
2016-06-13丁艳风何俊郑州升达经贸管理学院共同学科部河南郑州451191
丁艳风 何俊(郑州升达经贸管理学院共同学科部,河南郑州451191)
左右极限定理适用范围的应用
丁艳风何俊
(郑州升达经贸管理学院共同学科部,河南郑州451191)
摘要:求函数在某点处的极限,判断函数在某点处的连续性、可导性、求间断点并分类等时,都需要通过求极限来判断。而所有这些都有一个共性的问题摆在大家的面前:就是不知何时求左右极限,何时不用求左右极限。针对这样的疑惑,我们给出解除疑惑的关键:都需要用到一个起着关键作用的知识点:左右极限的适用范围,针对这些知识点及关键需要注意的地方我们做以下几点说明。
关键词:极限;连续;可导性;适用范围
何俊(1980-),河北邯郸人,郑州升达经贸管理学院共同学科部,副教授,主要从事数学教育,应用数学及灰色系统理论等方向研究。
Abstract:In order to calculate the limit of a function at a point,judge continuity and derivabilityof the function at a point and calculate the discontinuity point and its classification,limit should be calculated first.All of these have a common problem,that is,when to calculate the limit and when not to.As for such doubts,the key to solve these problems is all of these issues need to use a key point of knowledge,that is,scope of the right and left limit.In view of the knowledge point and the key,several problems should be paid attention to,which will be described in the paper.
Keywords:limit;continuity;derivability;scope
引言
极限是微积分的工具,在每一章节里都少不了求极限。在微积分的微分部分,有一个始终困扰学生的一个问题就是:对于函数趋于某点x0处的极限,什么时候需要求左右极限,什么时候不需要求左右极限,针对这样的困惑我们就微积分中常出现的、学生容易出错的地方来做一下简单说明。
一、左右极限定理
求函数在某一点处的极限有三种情况,第一种情况是x从x0的左边趋于x0,记为第二种情况是x从x0的右边趋于x0,记为x→x0,第三种情况就是x从x0的左右两边趋于x0,记为x→x0。前面两种情况初学者很容易理解,但是对于第三种情况,有些题目需要考虑左右极限才能求出结果,有些题目不需要考虑左右极限就可以直接求出。面对这种情况新学者一下子区分不开,就会出现我们刚开始说的情况。因为在这种情况下,相应的有下面的左右极限定理:
1.左右极限定理:
2.左右极限定理的使用范围:(1)左右极限定理主要用于求分段函数在分段点处,且在分段点处左右两侧表达式不同时的极限;
为了帮助学生理解这一点,我们最好举个例子:
这个函数虽然是分段函数,但是在分段点x=1处函数左右两边的表达式一样,从而就不用考虑左右极限了而是直接利用函数的性质就可以求出
(2)左右极限定理主要用于求含有绝对值(或开偶次方根)的函数在使绝对值为零处的极限。
此点有学生不容易理解的地方:在使绝对值为零处,为此我们可以举例如下:
此极限含有绝对值,且当x→3时|x-3|的值为零,所以求这类极限就要考虑左右极限。因为x从3的左右两边趋于3时,两种情况去绝对值后的函数表达式不同了。
同样也含有绝对值,但是当x→1时|x-2|的值不为零,所以求这样的极限就不需要考虑求左右极限。
下文例如4、例如5这两个极限都满足条件(3),所以要通过求左右极限来判断此极限是否存在。
解:
从而极限不存在。
在讲完此定理的同时一定要给学生详细的讲解一下左右极限定理的适用范围,只有把这几个适用范围记清楚了,在求函数趋于某点x0时的极限就不容易出错了。并同时指出这几点一定要记好,因为接下来后续几章都要用到。
二、左右极限定理适用范围在连续性中的应用
(一)判断函数在x0处的连续性
函数f(x)在x0处连续的定义:设函数f(x)在点x0处有定义,如果
则称函数f(x)在x0处连续。
由连续的定义知:判断函数在某点处是否连续,(1)首先得看看函数在这点处是否有定义;(2)其次若有定义再看看极限是否存在;(3)最后若极限存在再判断极限值是否等于函数值。一般题目中条件(1)一定满足,最重要的一步就是条件(2),而这一点就是求函数在某点处的极限是否存在,恰就是这一点是学生最容易出错,最不易理解的一点:何时求左右极限,何时不用求左右极限,原因就是对左右极限定理的适用范围这一点掌握的不好,这时我们不妨强调一下。举例如下:
这是一个判断分段函数在分段点处的连续性的问题,根据连续的定义需先判断极限是否存在,若存在,再判断极限值是否等于函数值f(0)。很显然分段函数在分段点x=0处左右两边表达式不同,从而由左右极限使用范围(1)知道需要求左右极限。
此函数也为分段函数,在分段点的左右两边表达式相同,但是却是适用范围(3)中的情况,从而求极限也需要求左右极限。
(二)函数的间断点及其分类
间断点分为第一类间断点和第二类间断点,而这两类间断点的定义也是从极限入手的。
间断点的定义:设x0为f(x)的间断点。
(1)若f(x)在x0处的左右极限都存在,则称x0为f(x)的第一类间断点。特别地,当左右极限相等时,即存在时,称间断点x0为f(x)的可去间断点;当左右极限不相等时,称间断点x0为f(x)的跳跃间断点。
(2)若f(x)在x0处的左右极限至少有一个不存在,则称x0为f(x)的第二类间断点。特别地,当左右极限中至少有一个为无穷大时,称x0为f(x)的无穷间断点。
由定义给初学者的错觉是判断间断点的类型都要考虑左右极限,只有通过左右极限才能判断间断点的类型。而实际上判断间断点的类型时用不用求左右极限全靠左右极限的适用范围,而只有熟悉这三点,针对相关题目的特点就一目了然。
根据函数间断点定义,可知初等函数的间断点只可能出现在函数无定义的点处:分母为零处或真数为零处;分段函数的间断点只可能出现在分界点处。相应的就有下面的例子。
例3:求下列函数的间断点,并判断间断点的类型。
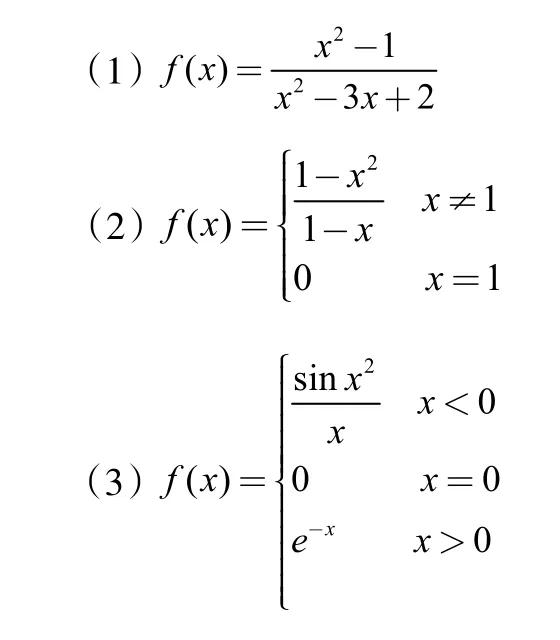
(1)为初等函数,很显然间断点只可能出现在使函数无定义处。x=1,x=2函数无定义,又在这两点处不满足左右极限的适用范围,所以在求极限时就不用考虑左右极限,直接求极限即可。(2)为分段函数,间断点只可能出现在分段点处,又在分段点左右两边函数表达式相同,不满足左右极限定理的适用范围,故在判断间断点的类型时也不用考虑左右极限。(3)也为分段函数,但在分段点左右两边函数的表达式不同,满足左右极限定理的适用范围,从而在判断间断点的类型时需要考虑左右极限。
解:(1)∵x=1,x=2时函数无定义,所以是间断点。
所以x=1为第一类可去间断点。
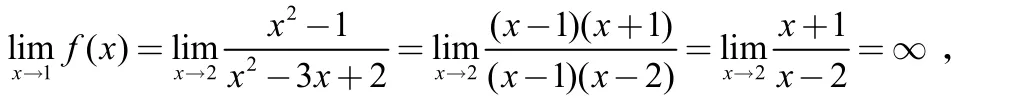
所以x=2为第二类无穷间断点。
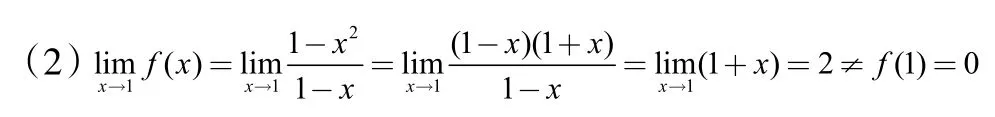
所以x=1为第一类可去间断点。
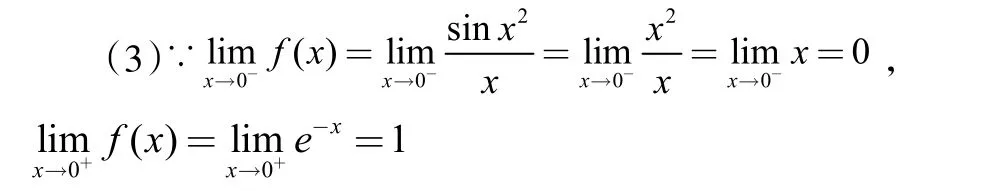
则f(0-0)≠f(0+0),所以x=0为第一类跳跃间断点。
三、左右极限定理在求导中的应用
求函数在x0处的导数一般情况下有两种做法:一种是用定义求,另一种是求出导函数,再把x0带入导函数即可。第二种方法很容易接受,难点在用导数定义求,特别是分段函数在分段点处的导数,这一直以来是大家的难点。因为函数在某点处的导数的定义也是通过求极限得到的,而且相应的还有左右导数定理。面对着定义和左右导数定理,使初学者认为,若用定义判断函数在点x0处是否可导,就必须求左右导数,从而增加了不必要的难度,还易出错。针对这种情况,我们以分段函数为例,用导数定义判断函数在点x0处的可导性。
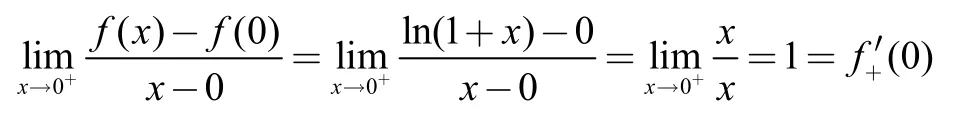
所以f'-(0)=f'+(0),从而f(x)在x=0处可导,且f'(0)=1。
所以f(x)在x=0处可导,且f'(0)=0。
左右极限的概念和计算是微积分教学的重点和难点,这个部分内容概念抽象,题型灵活多样,需要及时归纳总结,只有深刻理解基本概念,掌握好左右极限的适用范围,才不至于遇到题目时一筹莫展,而是很容易就找到解决问题的切入点和突破口。
参考文献
[1]成立社.微积分[M].郑州:郑州大学出版社,2007.
[2]赵树嫄.微积分(第三版)[M].北京:中国人民大学出版社,2007.
[3]统计大学数学系.高等数学(第六版)[M].北京:高等教育出版社,2006.
中图分类号:G0174
文献标志码:A
文章编号:2096-000X(2016)12-0255-03
作者简介:丁艳风(1979-),河南郑州人,郑州升达经贸管理学院共同学科部,讲师,主要从事数学教育,泛函分析算子理论等方向的研究。
