紫外可见分光光度法测定硅砂的不确定度评定
2016-06-13张凤萍
张凤萍
(太原重工理化检定中心,山西030024)
紫外可见分光光度法测定硅砂的不确定度评定
张凤萍
(太原重工理化检定中心,山西030024)
摘要:叙述了用紫外可见分光光度法测定硅砂中铁元素的不确定度评定过程,并得出测定方法的不确定度评定结果。
关键词:标准不确定度;硅石;紫外可见分光光度法
测量结果的不确定度表明该结果的可信赖程度。不确定度愈小,所述结果与被测量的真值愈接近,质量越高,水平越高,其使用价值越高;反之,测量结果的质量越低,其使用价值也越低。因此,结果的不确定度是测量结果必不可少的质量指标。对紫外可见分光光度法测定硅石中铁含量的不确定度进行评估,建立了数学模型,寻找测量过程中不确定度主要来源如标准物质、样品制备、曲线拟合以及重复实验等产生的不确定度,评定其扩展不确定度。
1测量条件和建立数学模型
1.1测量依据
测量依据为:GB/T 7143—2010《铸造用硅砂化学分析方法》,JJG 375—1996《单光束紫外可见分光光度计》。
1.2环境条件
环境条件为室温,正常大气压,湿度为45%~80%。
1.3测量设备
测量设备有:AB204—S型电子天平,可读性:0.1 mg,重复性 :⟨±0.1 mg。
TU—1810SPC型紫外可见分光光度计,光度准确度:±0.002 Abs(0~0.5 Abs),±0.004 Abs(0.5 Abs~1.0 Abs);光度重复性:0.001 Abs(0~0.5 Abs),0.002 Abs(0.5 Abs~1.0 Abs)。
以上设备均由山西省计量科学研究院检定合格,且在有效周期内使用。
1.4建立数学模型
式中ν1——分取试样溶液体积的数值,ml;
ν——试样溶液总体积的数值,ml;
m1——由回归方程求得分取试样溶液中氧化铁量的数值,mg;
m——试样质量的数值,g。
2量化分量不确定度
2.1分析不确定度来源
u1=A残差的不确定度
u2=仪器读数的标准不确定度
u3=测定重复性标准不确定度
u4=标准样品的标准值不确定度
um=试样称量的标准不确定度
urel(p)=标液纯度的相对不确定度
uT=标液体积的标准不确定度
urel(C)=标准曲线引起浓度c的标准相对不确定度
2.2测量程序
吸取浓度为1 000 μg/ml的纯铁标液(GSBG62020-90),配置成100 μg/ml标液,分别移取铁标准溶液0 ml、2 ml、4 ml、8 ml、10 ml于一系列100 ml容量瓶中,以水稀至20 ml,加入10 ml磺基水杨酸(30%),滴加入氨水(浓)至黄色并过量两滴,冷至室温,以水稀至刻度,混匀,以空白液为参比,2 cm比色皿,于紫外分光光度计波长为500 nm处测量吸光度A,测量结果如表1所示。
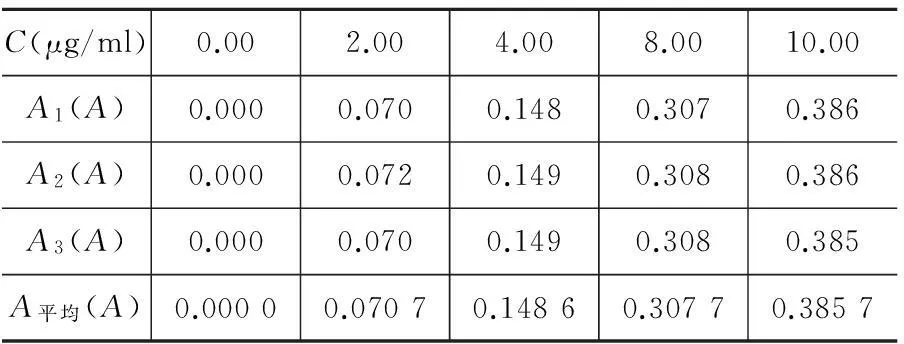
表1 测量结果Table 1 Measured results
称取1.000 0 g硅砂试样,溶解后,稀至100 ml容量瓶中,吸取10 ml于100 ml容量瓶中,加入10 ml磺基水杨酸(30%),再加入氨水(浓),冷至室温,按上述方法测定铁含量。
2.3标准工作曲线
根据测量数据及线性回归法求出标准工作曲线:
a=0.000 1
b=0.039 23
R=0.999 9
A=0.000 1+0.039 23C
2.4计算回归直线的标准偏差uc
2.4.1计算原则
实验室按照GB/T 7143—2010方法将纯铁标准溶液配制成几个浓度值C1、C2、C3……Cn的标准溶液,每个浓度的标准溶液均用紫外分光光度计测量m次,得到nm次个响应值A11、A12、A1m、Aij…..Anm,由一系列已知浓度值和响应值计算出线性方程,然后利用该线性方程确定其他溶液的浓度值,相对测量法的测量不确定度就是C与A之间有线性关系时该线性关系的不确定度。
根据朗伯-比耳定律:A=KCL,其中,A——物质的吸光度;K——物质的吸光系数;C——物质的量浓度;L——液层的厚度。
我们可以将A和C关系定义为数学模型:
A=a+bC
根据测量数据(Ci,Ai)验证C和A的线性关系,计算相关系数R,若R值大于0.995,则表明A与C之间成线性关系。
截距:
a=A-bC
2.4.2根据数学模型求方差和传播系数
标准曲线引起浓度C不确定度uc(c):uc(c)=(fA2uA2+fA2uA2+fb2ub2)1/2
传播系数:
fA=1/b
fA=-1/b
fb=(a-A)/b2
2.4.3标准曲线引起浓度C的标准相对不确定度urel(c)
(1)A残差的不确定度uA计算
残差的标准偏差SA=0.000 709 8A。uA是A残差的不确定度,按正态分布变化,属A类。uA=SA=0.000 709 8A。自由度:ν1=mn-2=13。
(2)斜率b的不确定度ub
ub=Sb
按正态分布属A类,故自由度为:ν=15-2=13。
传播系数:
fb=(a-A)/b2
(3)截距a的不确定度uA
uA=SA
按正态分布变化属A类不确定度,故自由度为:ν=15-2=13。
传播系数:
fA=-1/b
标准曲线引起浓度C的标准相对不确定度urel(c):
urel(c)=0.013 95
2.4.4紫外分光光度计仪器读数的不确定度u2
仪器光度准确度:(0~0.5)Abs±0.002 Abs,(0.5~1.0)Abs±0.004 Abs
仪器光度重复性:(0~0.5)Abs±0.002 Abs,(0.5~1.0)Abs±0.002 Abs
按均匀分布变化,属b类。
仪器读数不确定度:u2=0.002 582 Abs。
自由度:ν2=∝。
传播系数:f2=fA=25.490 6 μg/ml。
仪器读数引起浓度c的标准相对不确定度urel(2)=0.011 97。
2.4.5测量重复性标准不确定度u3
重复测量标准溶液11次,计算出各自的标准偏差,取其中最大值。
测量重复性相对不确定度:u3=0.002 43。
各测量值是随机量作A类,自由度:ν3=11-1=10。
2.4.6标准样品的不确定度u4
由GSBG62020-90标准样品供应商证书可知,扩展不确定度U=4 μg/ml,K=2,相对不确定度urel(p)=0.000 2。
2.4.7试样的标准不确定度
2.4.7.1试样称量的标准不确定度um
在天平上称取1.000 0 g试样,称取程序按差量法进行,两次称量的每一次都受变动性和天平校准不确定度的支配,校准本身有两个不确定源:灵敏度和校准函数的线性。因为在同一天平上并在小的质量范围内称量,灵敏度可忽略。
天平制造商给出了±0.2 mg的线性分量,可读性 0.1 mg,按矩形分布,属b类。
质量引起的不确定度:um=0.182 6 mg。
质量相对不确定度:urel(m)=0.000 182 5。
2.4.7.2标样体积不确定度
校准:制造商明示:在20℃左右测定容量瓶的体积(50±0.05)ml、(100±0.10)ml、(1 000±0.3)ml、(10±0.02)ml,假定为三角形分布。
计算标准相对不确定度为0.000 921。
温度:制造商规定容量瓶校准温度为20℃,而实验室温度在20℃±4℃的范围内变化,计算温度对1 000 ml、50 ml容量瓶、10 ml移液管的标准相对不确定度为uT=0.000 84。
重复性:通过对容量瓶重复实验可以估算定容变动重复性不确定度。
标准偏差为(10±0.017 78)ml、(50±0.053 9)ml、(1 000±0.2)ml。
标准相对不确定度:urep=0.002 089。
试样体积相对不确定度:urel(V)=0.002 433。
2.8合成样品的相对不确定度u4(rel)
u4(rel)={urel(c)+urel(2)+u3+urel(m)+urel(p)+urel(V)}1/2=(0.013952+0.011972+0.002432+0.00018252+0.00022+0.002433 2)1/2=0.0187
合成标准样品的不确定度u4:
u4=cu4(rel)=0.11 μg/ml
2.9扩展不确定度
扩展不确定度为:
U=tp(V)uc
取置信水平p=95%,查t分布表得:
k=2.00
U=2.00×0.11=0.22 μg/ml
w=[C×10-3/1.0000]×100%
2.10不确定度评定报告
此次紫外可见分光光度计铸造用硅砂测量中铁含量的扩展不确定度报告为:
(0.550±0.022)%,k=2.00,置信水平p=95% 。
3结论
(1)由于测量结果的不确定度往往由多种原因引起,本文通过实验对观测列进行统计分析的方法来评定A类标准不确定度分量,由重复性引起的不确定度的来源,用标准偏差计算出A类不确定度分量,比较客观。
(2)测量仪器的不确定度是保证测量结果准确可靠的首要条件。在不确定度满足预期使用条件下,还应考虑其他测量特性,如稳定度、量程、分辨力等特点。如天平、紫外分光光度计仪器本身带来的不确定度来源,根据说明书等信息进行B类不确定度评定。
(3)容量瓶、移液管等计量器具引起的测量不确定度,我们用经验“如最大测量误差允许值”去合理评定其不确定度。
(4)总之,我们根据不确定度不同来源进行了辨别,并在此基础上对测定过程中的不确定度分量进行了合理评定。测量不确定度主要来源于试样称量、标准溶液配制、校准曲线拟合、各种玻璃量器的使用及测量重复性。做到不漏掉大的不确定度来源,同时也不忽略细小的来源,依据不确定度评定的步骤,分析和计算尽量对不确定度分量进行合理评定。
(5)根据得到的各分量标准不确定度,合成标准不确定度,最后合成标准不确定度乘以 95%置信概率下的扩展因子约2获得测量结果的扩展不确定度。
编辑杜青泉
Evaluation on Determining Uncertainty of Silica Sand by Ultraviolet Visible Spectrophotometry
Zhang Fengping
Abstract:The evaluation process for determining the uncertainty of Fe in the silica sand by means of ultraviolet visible spectrophotometry has been described.Meanwhile,the evaluation results of uncertainty with this determining method have been obtained.
Key words:uncertainty of standard;silica;ultraviolet visible spectrophotometry
收稿日期:2016—01—27
作者简介:张凤萍,女,高级工程师,主要从事化学分析研究。电话:18636976619,E-mail:zfpd-119@163.com
中图分类号:O657.32
文献标志码:B
