求三角函数最值问题的策略
2016-06-12重庆梁明龙
高中数理化 2016年10期
◇ 重庆 梁明龙
求三角函数最值问题的策略
◇重庆梁明龙
三角函数最值问题是函数最值的重要组成部分,是历届高考的热点,此类问题不仅与三角基础知识密切相关,而且与代数中的二次函数、一元二次方程、不等式及某些几何知识的联系也很密切.三角函数的最值问题有以下几种类型.
1形如y=asin x+b(或y=acos x+b)型
策略利用|sinx|≤1(或|cosx|≤1),即可求解.

解函数y=acosx+b的最值与a的符号有关,故需对a分类讨论.
当a=0时,不合题意;
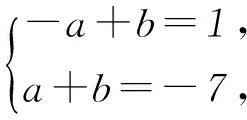
当a=4,b=-3时,
bsinx+acosx=-3sinx+4cosx=
当a=-4,b=-3时,
bsinx+acosx=-3sinx-4cosx=

所以bsinx+acosx的最大值为5.
2形如y=asin x+bcos x型


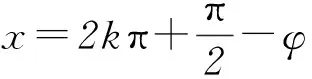

3形如y=asin2x+bsinx+c(或y=acos2x+bcosx+c)型
策略对含有sinx、cosx,并且其中一个是二次,处理方式是应用sin2x+cos2x=1,使函数式只含有一种三角函数,再应用换元法,转化成二次函数来求解.

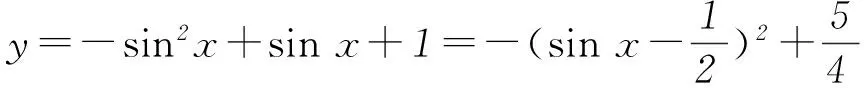


策略对于一个分式,分子、分母分别含有正、余弦的一次式.常利用正、余弦函数的有界性,将其转化为关于y的不等式求解,也可以用圆的参数方程或斜率公式求解.

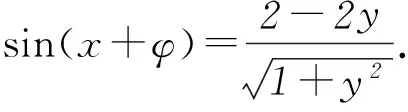

总之,求三角函数最值的常用方法有: 1) 配方法(主要利用二次函数理论及三角函数的有界性); 2) 化为一个角的三角函数(主要利用和差角公式及三角函数的有界性); 3) 数形结合法等.
(作者单位:重庆市大足中学)
