整体换元思想在数列中的应用

◇　广东　戴元涛



整体换元思想在数列中的应用

◇广东戴元涛

整体换元作为一种巧妙的解题方法,为数学解题提供了便利．数列问题是运用整体换元思想最常见的载体．本文根据换元法在数列方面的应用进行分类举例．

1利用等差数列的性质

A-90;B90;C-110;D110

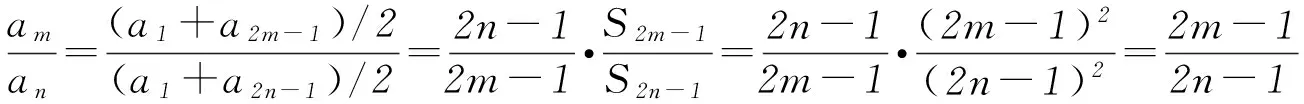
2利用等比数列的性质

因为a1>0,所以a2n-1>0,故a3+a5=4．

A12;B10;C8;D2+log35

log3(a1·a2…a10)=log3(a5a6)5=

5log39=5×2=10,故应选B．

3直接利用前n项和进行整体换元

解得S奇=162,S偶=192．

所以由S偶-S奇=6d=30,解得d=5．

设a2+a3+…+an=x,则原式可化为

(a1+x)(x+an+1)-x(a1+x+an+1)=

a1x+a1an+1+x2+xan+1-a1x-x2-xan+1=a1an+1.

综上,通过整体换元思想在解答高考数列问题中的应用,降低了考题的难度,使问题简单化,能够提高考生的解题效率,大大缩短了解题时间,为检查提供了保障．所以在数学学习中有意识地渗透整体思维,一定会有所收益．同时整体换元思想使考生在整体上对问题进行分析和把握,考虑问题更加全面、思维更加灵活,在解题的过程中不断总结与实践,拓宽了解决问题的途径,提高了解决问题的能力,同时也丰富了自己的阅历．

(作者单位：深圳市坪山高级中学)