基于压缩感知的OMP改进重构算法

王军,孔令斌,赵洁

(西安邮电大学a.通信与信息工程学院; b.电子工程学院,西安 710121)



基于压缩感知的OMP改进重构算法

王军a,孔令斌a,赵洁b

(西安邮电大学a.通信与信息工程学院; b.电子工程学院,西安 710121)

摘要:针对无线通信网络近些年出现的大数据量信号的情况,在对信号采样的同时进行适当压缩,利用合适的重构算法实现了用少量的采样值或观测值对信号进行重构。在原有基于OMP(正交匹配追踪)的压缩感知重构算法的基础上引入AS(交替步长),提出一种新的改进算法——GP-OMP(梯度正交匹配追踪)算法。实验结果表明,该改进算法利用前一感知时刻获得的频谱信息,不仅能有效地降低重构算法的计算量,还能有效地减少重构耗时,并得到与原有方法基本一致的重构效果。

关键词:重构算法;压缩感知;交替步长;频谱感知

0　引 言

近年来,一种新型的采样理论——压缩感知[1]在信号处理领域诞生。该理论的突出优点是将传统的数据压缩与数据采集结合起来。重构算法是信号处理领域和应用数学中一个新的研究方向,是压缩感知理论的一个关键部分,它涉及到压缩信号的精确重构和采样过程中的准确性验证。我们在实践中使用了不同的优化算法,其中凸优化算法中使用了BP(基追踪)、LARS(最小角度回归)[2]和GPRS(梯度投影的稀疏重构)[3]。近年来,贪婪策略已被广泛使用,在某些情况下它比推算的方法具有更好的性能。在MP(匹配追踪)中,OMP[4](正交匹配追踪)、正则OMP[5]和稀疏自适应MP[6]均为贪婪算法。通过将MP与优化算法相结合,从而推导出新的算法——DP(定向追踪)[7]算法。OMP[8]算法是常用的一种信号重构算法,但是当信号长度很长时,信号重构过程耗时会更长,频谱感测的实时性会受到影响。

本文首先分析了压缩感知的基本理论和现有的重构算法,然后通过使用AS(交替步长)法,即基于所述优化理论改变步长来改善GP(梯度追踪)算法,以克服最速下降步长大小的锯齿现象,最后与OMP算法组成新的改进算法。结果表明,该方法不仅可以大大减少信号重构算法的耗时,还可以达到与现有OMP算法基本一致的重构效果。

1　压缩感知理论

目前,对压缩感知理论的研究已有了很大的进展,其中针对重构算法的研究,一些学者提出了贪婪算法,但这类算法重构精度比较低,且耗时较多;而另一些学者则提出了基于贝叶斯的压缩感知方法。此外,还有很多需要解决的问题。

1.1压缩感知的基本框架

压缩感知理论是新的信号采样、编码和解码理论。信号的采样速率不仅与带宽有关,还与信号的结构和位置密切相关。编码过程是一种优化的算法,是围绕观测矩阵展开的。该理论已经被证实,即以一个相对较低的采样速率对信号进行正确采样,能以很高的概率重构出原始信号。

压缩感知理论框架如图1所示,主要包括稀疏信号的3个步骤:首先,如果信号x∈RN(R为实数,N为维数)在某个正交基或紧框架Ψ上是可压缩的,则计算变换系数Θ=ΨTx,Θ为Ψ的等价或近似稀疏表示;然后,设计一个平稳变换基Ψ和不相关的M×N观测矩阵Φ,对Θ进行观测,得到观测集合=ΦΘ=ΦΨTx;最后,使用0-范数意义下的优化问题求解x的精确或近似逼近:min‖ΨTx‖0s.t ACSx=ΦΨTx=,

式中,s.t表示条件,ACS为信息算子,求得向量x在稀疏基上的最佳表示。

图1　压缩感知理论框架

1.2压缩感知采样过程

1.2.1信号的稀疏性定义

信号的稀疏性或可压缩性是压缩感知理论的一个重要前提和基础。但在现实中,信号通常是不稀疏的,需要在某个变换域下逼近稀疏,常用的方法是对信号进行正交变换使其稀疏或可压缩。为了简化模型,通常考虑离散信号x的长度为N,即x=[x1, x2,…,xN]T,由信号理论可知,x可以用一组基ΨT={Ψ1,Ψ2,…,ΨN}线性表示,即

式中,S是对x进行稀疏后的N×1维向量,其中大多数元素的值为0。稀疏表示的原理是通过线性空间的映射将信号在稀疏的空间进行表示。Ψ是N× N维信号x的稀疏基矩阵。

1.2.2压缩感知的线性测量过程

压缩感知的核心是线性测量过程。记x为采样得到的长度为N的信号,可以通过压缩感知直接获得长度为M(M< N)的重构信号∶=Φx。对原始N维信号x进行观测,获得M维向量信号,然后利用优化方法从观测值中高概率地恢复出原始信号x。如果信号x是不稀疏的,则可以在正交稀疏交换下用系数向量S表示为x=ΨS,其中S为K稀疏,即只有K个非零元素,因此测量过程可以表示为

式中,Θ=ΦΨ为M×N维矩阵。由于信号是K稀疏的,因此用K个系数就能够从M个测量值中准确地重构出原始信号x(得到一个最优方案)。

为了保证算法的收敛性,使K个系数可以通过M个测量值精确恢复,感知矩阵Θ必须满足RIP(限制等距性)[9],即对任何具有K稀疏的矢量v,矩阵Θ都能保证如下不等式成立:

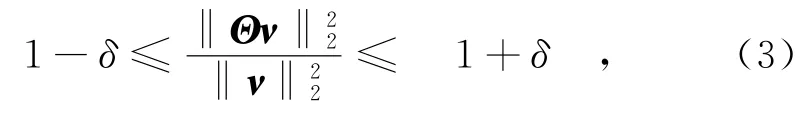
式中,0<δ<1。RIP的等效情况是测量矩阵Φ和稀疏基Ψ不满足相关要求,保证观测矩阵不会把两个不同的K稀疏信号映射到同一个集合。

1.2.3压缩感知稀疏重构过程

由于最优化问题与信号稀疏分解中的优化问题非常相似,11范数最小问题在一定条件下与l0范数最小问题是等价的。为了得到相同的解决方案,上式可转化为11范数的最小优化问题,即min‖S‖l1s.t.=ΦΨS,也被称为BP。贪婪算法

2　压缩感知重构算法研究

如何设计出复杂度更低、更精确、更稳定且所需观察数目较少的重构算法,始终是压缩感知理论信号重构问题的主要研究方向。在现阶段,我们所知道的压缩感知重构算法大致可以分为以下几类:贪婪迭代算法、凸优化算法或最优化逼近方法、基于贝叶斯的重构算法和其他重构算法。

2.1最速下降法的相关理论

最速下降法基于最优化理论。针对无约束极小值问题min f(x)=(xTAx)/2-bTx,式中,A为对称正定矩阵,假设函数f(x)是连续可微的,且其在点xk的梯度为gk=∇f(xk),考虑函数的泰勒展开式为记x-xk=akdk,其中,ak为一数值,dk是n维列向量,则满足(dk)Tgk<0的方向是dk下降方向。当且仅当dk=-gk时,(dk)Tgk最小,从而-gk是最速下降方向。以这个方向为搜索方向,搜索找到迭代函数的最小值,这就是已知的最速下降法。

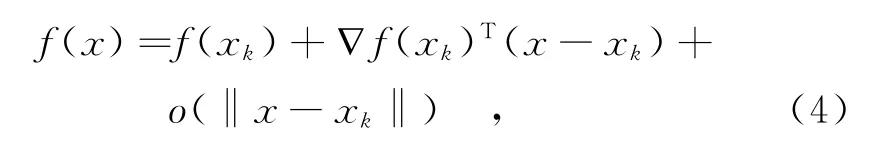
最速下降法的迭代模式为xk+1=xk-akgk,且其步长ak满足,解决最优化问题必须满足,由此可得为最速下降步长。由于在求解过程中当前负梯度方向相互垂直,导致搜索路径呈锯齿形,因此采用这种方法来搜索最优解时会走很多弯路,影响了算法的收敛速度。

2.2GP算法的改进

由于GP算法是基于最速下降法的,在进行迭代求解时步骤最快,导致相邻的两个搜索方向互相垂直,搜索路径呈锯齿形,因此影响了算法的收敛速度。针对GP算法的这一缺点,本文提出了使用AS法对原步长进行改善。

基于最优化理论中的最速下降法,每次迭代都致力于使重构误差最小化,n次迭代的误差函数可表示如下:

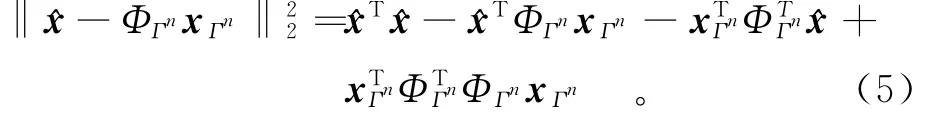
本文采取改变或缩短步长的策略来提高收敛速率,即AS法。AS法是将BB(两点步长梯度法)步长aBB和最速下降步长aSD交替使用,交替方式如下:

3　改进的GP-OMP算法

改进算法不使用计算量巨大的最小二乘法求解,而是沿着负梯度方向搜索得到最优解,该算法是OMP算法和最速下降法的完美结合。在本文中,我们采用缩短搜索步长的方法,不用在每次迭代过程中都追求目标函数值,从而避免了搜索路径呈锯齿形。实验结果表明,改进的算法可以在一定程度上缩短信号重构的耗时,提高重构效率。

3.1算法步骤

用于信号稀疏重构的改进后的GP-OMP算法步骤可总结如下:

输入:感知矩阵Φ,测量向量z,稀疏度K;

初始化:余量r°=z,重构信号x°=0,索引集Γ°=φ,迭代次数n=0;

步骤1:计算余量和感知矩阵Φ的每一列的内积gn=ΦTrn-1;

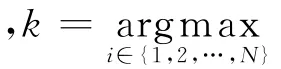
步骤7:更新余量rn=rn-1-ancn;

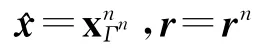
3.2仿真与结果分析

为了验证GP-OMP算法的性能,本文基于windows下的MATLAB仿真环境实现了改进的算法,并与原有的OMP算法做了性能比较。

仿真实验采用一维信号,信号长度N=512,稀疏度K=10,观测信号长度为80,并采用相同的感知矩阵。定义信号如下:x=0.3sin(100πt)+ 0.6sin(200πt)+0.1sin(400πt)+0.9sin(800πt);压缩矩阵为高斯随机采样矩阵,采样点数由公式M≥K*log(N/K)确定。

OMP算法与改进的GP-OMP算法重构结果的对比如表1所示。由表1可知,改进后的GP-OMP算法的重构时间较长,这是因为PSNR越高,信号重构效果越好,所需重构时间也就越长。改进后的算法与原有的OMP算法相比,重构质量更好,并具有相似的重构时间成本。

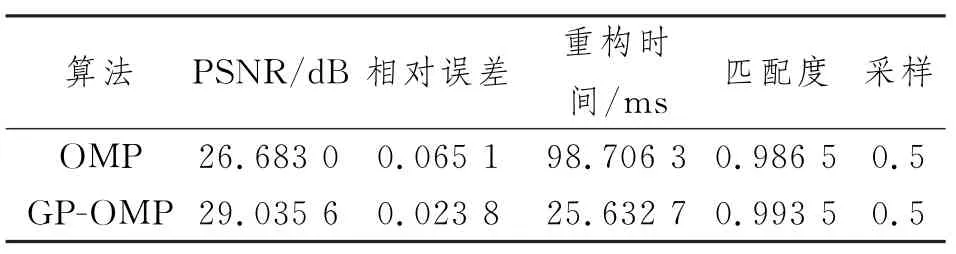
表1　OMP算法与改进的GP-OMP算法重构结果的对比

为了更充分地测试GP-OMP算法的实时性,对GP-OMP和OMP算法在不同稀疏度和不同信号长度下的耗时进行了比较,结果分别如图2和图3所示。从图2可以看出,信号稀疏度较低时,OMP算法耗时比GP-OMP算法高;随着信号稀疏度的增大,两种算法的耗时都增大,且耗时的差距越来越大。这是因为在决定重构频谱相位时,随着稀疏度K的增大,在步骤流程中OMP算法的计算量越来越大。从图3可以看出,随着信号长度N的增大,两种算法的耗时都有所增加,但GP-OMP算法的耗时远低于OMP算法。这是因为随着N的增大,重构矩阵和相对误差的每一列长度也会相应增加,导致重构算法的耗时也相应增加。

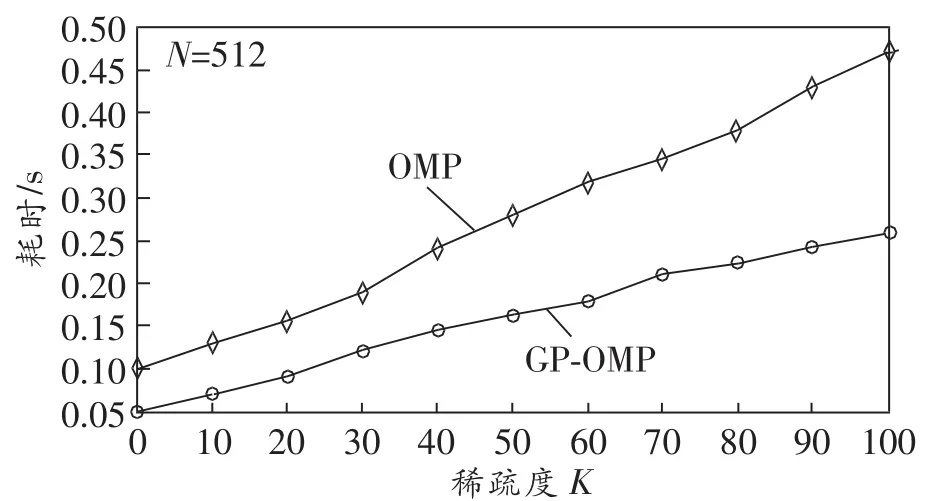
图2　不同稀疏度下两种算法耗时比较

图3　不同信号长度下两种算法耗时比较

4　结束语

对于稀疏或可压缩的信号而言,压缩感知作为一种新的信号采样方法,比传统的采样方法更为有效。在压缩感知理论中,采用最小二乘法优化算法的信号重构不再适用,而采用不同的凸优化和贪婪算法对信号进行重构成为压缩感知的研究重点。本文针对梯度法在搜索步长上的缺陷,引入了AS法,并通过实验仿真验证了该方案的可行性。仿真结果表明,改进后的算法在不同程度上改善了信号的重构耗时和重构质量,虽改进不多,但是一种新的尝试和探索。GP-OMP算法在前一感知时刻获得信道信息,不仅大大减少了计算量,还能有效地减少耗时,达到与OMP算法基本一致的重构效果,提高了压缩感知的实效性。

参考文献:

[1] Tuuk P B,Marple S L.Compressed sensing radar amid noise and clutter using interference covariance information[J].IEEE Transactions on Aerospace& E-lectronic Systems,2014,50(2):887-897.

[2] Candès E,Romberg J,Tao T.Stable signal recovery fromincomplete and inaccurate measurements[J]. Comm Pure Appl Math,2006,59(8):1207-1223.

[3] Figueiredo M,Nowak R,Wright S.Gradient projection for sparsereconstruction:Application to compressed sensing and other inverseproblems[J].IEEE Journal of Selected Topics in Signal Processing,2007, 1(4):586-597.

[4] Tropp J,Gilbert A .Signal recovery from randommeasurementsvia orthogonal matching pursuit[J]. IEEE Trans Inform Theory,2008,53(12):4655-4666.

[5] Needell D,Vershynin R.Signal recovery from incomplete and inaccurate measurements via Regularized Orthogonal Matching Pursuit.Submitted for publication [J].Selected Topics in Signal Processing,2007,4 (2):310-316.

[6] Thong T Do,Lu Gan,Nam Nguyen,et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Asilomar Conference on Signals, Systems,and Computers 2008.Pacific Grove,California:IEEE,2008:581-587.

[7] Blumensath T,Davies M E.Stagewise Weak Gradient Pursuits[J].IEEE Trans on Signal Processing,2009, 57(11):4333-4346.

[8] Aguilera E,Nannini M,Reigber A.A Data-Adaptive Compressed Sensing Approach to Polarimetric SAR Tomography of Forested Areas[J].Geoscience& Remote Sensing Letters IEEE,2013,10(3):543-547.

[9] Blumensath T,Davies M E.Gradient pursuits[J]. IEEE Trans on Signal Processing,2008,56(6): 2370-2382.

An Improved Reconstruction Algorithm for Compressed Sensing-Based OMP

WANG Juna,KONG Ling-bina,ZHAO Jieb
(a.School of Communication and Information Engineering;
b.School of Electronic Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710121,China)

Abstract:In view of the emergence of mega data signals in wireless communication networks in recent years,this paper properly compresses these signals while performing signal sampling and realizes their reconstruction with small amount sampling value or observed value by using an appropriate reconstruction algorithm.On the basis of the original Orthogonal Matching Pursuit(OMP)-based compressed sensing reconstruction algorithm,the Alternating Step-size(AS)is introduced and an improved algorithm,i.e.GP-OMP algorithm proposed.Experimental results show that the spectrum information this algorithm obtained by using the previous sensing moment can not only effectively reduce the amount of computations by the reconstruction algorithm,but also the reconstruction time,with almostthe same results as those by using the original method.

Key words:reconstruction algorithm;compressed sensing;alternately step;spectrum sensing

中图分类号:TN911.23

文献标志码:A

文章编号:1005-8788(2016)01-0074-05

收稿日期:2015-06-29

作者简介:王军(1989-),男,甘肃平凉人。硕士研究生,主要研究方向为信号与信息处理。

doi:10.13756/j.gtxyj.2016.01.022