船-桥碰撞有限元数值模拟分析

左玉强

(合肥工业大学 土木与水利工程学院，安徽 合肥　230009)



船-桥碰撞有限元数值模拟分析

左玉强

(合肥工业大学 土木与水利工程学院，安徽 合肥230009)

摘要：文章以船-桥墩碰撞为主要研究对象，重点探讨碰撞过程中撞击力、撞深的变化以及速度对撞击结果的影响，利用LS-DYNA进行数值模拟，仿真分析船舶在不同初始速度情况下的撞击结果，并与各国规范进行比较，同时分析船舶刚度对撞击结果的影响，为桥墩防护设计提供参考依据。

关键词：船-桥碰撞；有限元；数值模拟；撞击力；桥墩

本文以安徽省望东长江公路大桥为背景进行船-桥相撞数值仿真分析，大桥采用主跨为638 m的5跨半漂浮体系斜拉桥。标准桥面宽为34.5 m，主梁为钢箱梁，下部为群桩基础，通航等级为Ι级，桥型布置如图1所示。

图1　全桥布置图

1有限元计算模型

1.1船-桥碰撞模型

根据望东长江大桥所在流域通航要求，本文采用10 000DWT级散货船作为代表船只进行仿真分析，船体长为120 m，宽为20 m，型深为9.7 m，吃水为7.55 m，初始航速为10节(5 m/s)。该桥设计最高水位为20年一遇洪水位18.97 m，本文研究该水位下船舶与桥墩的碰撞，为节约计算时间，只建立桥墩模型，群桩基础对墩台的作用模拟为墩台底部的固结，上部荷载按均布荷载施加于桥墩上，在桥墩上方添加质量块模拟均布荷载。

1.2有限元模型

船舶模型采用球鼻艏，为了减少计算成本和精确模拟船艏部分的撞击情况，船艏采用较细的网格划分，船身采用粗网格，有限元模型如图2所示。

为了近似模拟船的刚度，船艏内部采用分层和纵梁模拟船艏刚度，通过改变船艏内部纵梁和横隔板的厚度模拟不同刚度。船舶采用Shell163单元[1]，船艏为钢结构，主要材料为Q235钢，应用弹-塑性材料模型模拟。材料弹性模量E=2.1×1011Pa，泊松比为0.28，屈服应力为2.35×108Pa，切线模量Et=2.1×108Pa，失效应变FS为0.35。船身处理为刚体，通过增加船身部分刚体单元密度模拟船体总质量。船舶初始速度为10节(5 m/s)，船与桥墩的静摩擦系数取0.3，动摩擦系数取0.25。为了考虑撞击过程中周围水体对碰撞的影响，采用附加质量法近似模拟，附加水体质量根据经验公式估计取0.04m[2](m为船体总质量，通过增加部分船体单元密度实现)。

图2　船舶有限元模型

对于桥墩有限元，由于碰撞损伤变形具有明显的局部性[3-4]，所以只在主要碰撞区域采用细网格，其他部位采用较粗网格进行划分。

桥墩主要材料为钢筋混凝土，建模时只建立实体单元模拟混凝土，钢筋作用可通过适当提高混凝土弹性模量近似模拟。混凝土材料密度为2 650 kg/m3，弹性模量为3.3×1010Pa，泊松比为0.167。桥墩采用Solid164单元，混凝土模型采用Hjc损伤模型[5-6]。

2LS-DYNAs计算结果分析

全船有限元模型共有Shell单元23 452个，其中船艏部分单元为15 070个；桥墩模型Solid单元共127 400个，其中碰撞区域单元为90 000个。

2.1船舶刚度对撞击力的影响

船-桥碰撞过程伴随着能量的转换，碰撞过程中船艏会发生较大变形，船舶初始动能大部分会转换为船舶的变形能，而桥墩只会吸收少部分能量[7]。

船舶刚度通过内部纵横结构厚度控制，在结构形式和材料相同的情况下，可认为厚度越大刚度越大。假设3种不同刚度，其厚度分别为为5 mm、15 mm、20 mm。由于构件厚度变化引起的质量增量计算入船身部分，以保证初始动能相同。通过数值模拟3种不同刚度船舶正向撞击桥墩，结果如图3所示。

图3　刚度对撞击结果的影响

由图3可知，船舶刚度对撞击结果有着直接影响，通过数值模拟结果分析可以看出，刚度越大，撞击力越大，碰撞接触时间却越短。

2.2撞击力时程曲线与经验公式比较

撞击力的简化计算方法有很多种[8]，分别为沃辛计算经验公式、我国规范[9]给出的最大撞击力计算公式、美国AASHTO简便计算公式、 欧洲规范撞击力计算公式、 沃辛修正公式、 挪威公共道路局规范公式及北欧公共道路局规范公式。

现以上述船舶最大刚度正撞时撞击力时程曲线与各规范计算结果进行比较，结果如图4所示。

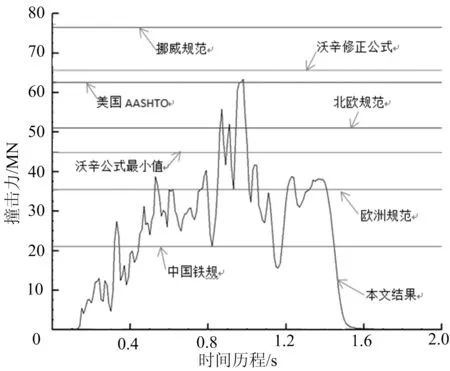
图4　结果比较图

由图4可知，计算机数值模拟结果撞击力是随时间不断变化，大约0.12 s时刻碰撞开始，撞击力逐渐增大，约为0.98 s时刻,撞击力达到最大值为63.4 MN，随后撞击力呈下降趋势，最终约在1.56 s时刻撞击力归为0，同时撞击过程基本停止，虽然撞击过程不超过2 s，其造成的损害却是巨大的。

各国规范根据经验公式计算得到的最大撞击力相互之间有着较大的差异，中国铁路规范[9]由于变形系数采用默认值，结果相对偏小，本文数值模拟结果撞击力最大值与美国AASHTO规范计算和沃辛修正公式计算结果比较接近。

2.3不同航速时撞击力及撞深

船舶航速大多在10节到20节不等，根据动能公式可知，速度越大动能越大，撞击过程也是能量转换的过程，很明显撞击前船舶的速度对结果有一定的影响。各国规范在关于撞击力计算公式中并不是都有初始速度这一控制变量，沃辛经验公式是在初始速度为8 m/s的情况下提出的，并没有考虑速度变化对结果的影响，包括北欧和挪威规范公式都没有考虑速度，中国铁规、美国AASHTO、欧洲规范等将速度视为主要控制变量，修正的沃辛公式也能适应速度的变化。本文现以初始速度为唯一变量研究撞击力的变化，并与各国规范进行比较，结果如图5所示。

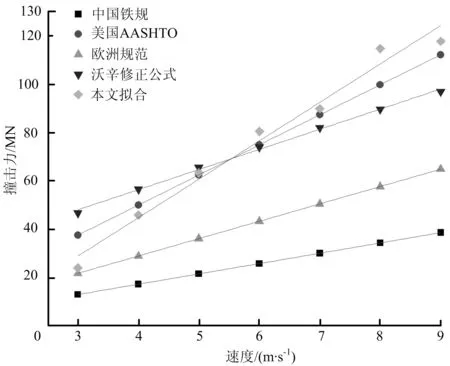
图5　速度对撞击力的影响

图5中棱形实心点为数值模拟结果，将撞击力与速度的关系拟合成线性关系。根据图中结果，可以看出各规范计算的撞击力大小与初始速度之间存在着明显的线性关系，而本文数值模拟结果也具有相似的线性关系。当速度是唯一变量时，初始速度越大，撞击力越大，美国AASHTO计算结果与本文数值模拟结果最为相似。

因为船舶质量是确定的，速度越大，则船舶的总体动能也就越大，碰撞过程中能量是守恒的，船舶的动能大部分转化为船艏的变形，小部分被桥墩吸收，所以速度对碰撞后的损害情况也产生较大影响。

图6所示为不同初始速度时撞深随时间变化曲线，随着速度增加，撞击深度变化基本相同，但最大撞击深度在逐渐增大，这就表示速度增加，船舶初始动能变大，最终造成较大的撞击深度。

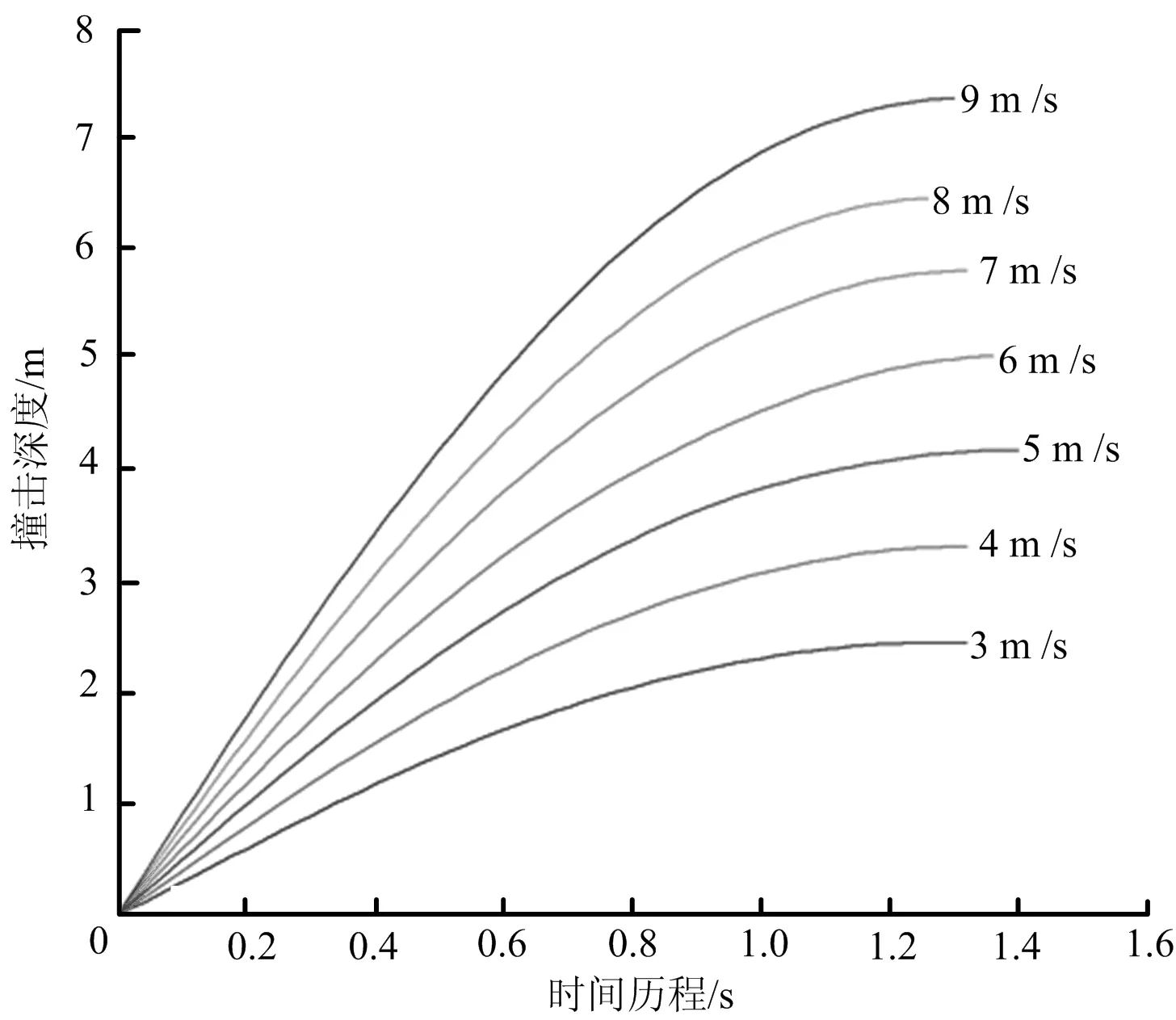
图6　撞击深度曲线

图7所示为桥墩损伤面积随速度变化曲线，随着速度增加，桥墩表面的损伤面积也在增加，其原因是碰撞能量在增加，并且与船艏前面尖后面宽的特殊结构形式有关。

图7　速度对桥墩损伤的影响

3结论

(1) 船桥碰撞过程是复杂的非线性动力问题，要模拟真实碰撞，模型参数选取很重要[10-11]，本文船舶模型参考了真实船舶尺寸，桥墩模型则根据实际工程确定。

(2) 目前各规范关于撞击力的计算公式基本都是最大撞击力的计算简式，各规范考虑因素不尽相同，文献[9]考虑了变形系数和折减，但实际工程变形系数难以确定，应用并不方便；美国规范简化公式只与船舶速度和吨位有关；欧洲规范则考虑了船舶刚度的作用，如果船舶刚度采用远洋标准，欧洲规范和美国规范公式计算结果基本相同。

(3) 碰撞过程中，碰撞能量基本转化为变形能，数值模拟中反映为船舶撞深，速度越大，相应初始动能越大，碰撞能量也就越大，所以撞深与速度也存在一定的正比关系，即速度越大相应的撞深也越大，同时撞击力也越大。

(4) 船-桥碰撞撞击力受多方面因素的影响，本文主要研究速度及撞击角度对结果的影响，根据结果可知，在实际应用中，当撞击不可避免时，降低航速以及改变撞击方向可以明显降低撞击的后果。

(5) 数值模拟分析结果受有限元模型及网格的影响较大，建立理想模型并在硬件条件允许的情况下，尽量使用质量好的细网格，减小沙漏影响，这样获得的结果可靠性更强。

〔参考文献〕

[1]何勇,金伟良,张爱晖,等.船桥碰撞动力学过程的非线性数值模拟[J].浙江大学学报(工学版),2008,42(6):1065-1070.

[2]王自力，蒋志勇，顾永宁.船舶碰撞数值仿真的附加质量模型[J].爆炸与冲击,2002，22(4):321-326.

[3]刘建成，顾永宁.基于整船整桥模型的船桥碰撞数值仿真[J].工程力学，2003，20(5)：155-162.

[4]吴永固，耿波，汪宏.桥梁船撞动力有限元数值模拟分析[J].重庆交通大学学报(自然科学版)，2010,29(5)：681-684.

[5]刘建成，顾永宁.船-桥碰撞力学问题研究现状及非线性有限元仿真[J].船舶工程，2002(5)：4-9.

[6]熊益波，陈剑杰，胡永乐.混凝土Johnson-Holmquist本构模型灵敏参数的初步确认[J].兵工学报，2009,30(2)：145-148.

[7]Consolazio G R, Cow an D R. Nonlinear analysis o f barge crush behavior and its relationship to impact resistantb Bridge design[J].Computers and Structures,2003,81(8/11):547-557.

[8]胡志强，顾永宁，高震，等.基于非线性数值模拟的船桥碰撞力快速估算[J].工程力学,2005,22(3):235-240.

[9]TB 10002 D1-2005,铁路桥涵设计基本规范[S].

[10]Consolazio G R,Asce A M,Cowan D R.Numerically efficient dynamic analysis of barge collisions with bridge piers[J].Journal of Structural Engineering,2005,131(8):1256-1266.

[11]Yanyan S,Hong H.Nonlinear finite element analysis of barge collision with a single bridge pier[J].Engineering Structures,2012(41):63-76.

收稿日期：2016-03-02

作者简介：左玉强(1991-)，男，安徽庐江人，合肥工业大学硕士生．

中图分类号：U661.42

文献标识码：A

文章编号：1673-5781(2016)01-0022-03