期望成本最优的土质高边坡坡角设计研究
2016-06-12方诗圣张云峰
杨 敏, 方诗圣, 张云峰
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009;2.安徽省高等级公路工程监理有限公司,安徽 合肥 230601)
期望成本最优的土质高边坡坡角设计研究
杨敏1,方诗圣1,张云峰2
(1.合肥工业大学 土木与水利工程学院,安徽 合肥230009;2.安徽省高等级公路工程监理有限公司,安徽 合肥230601)
摘要:在高边坡总期望成本中考虑了生态成本,参照矿山建设对环境的影响研究将其分为征地成本和环境损失成本。提出了包含生态成本的高边坡综合治理的期望成本目标函数,对目标函数施加了保证安全与可行性的约束条件,建立了高边坡期望成本模型。结合边坡的可靠度理论和优化设计理论,提出了求解该模型的计算步骤。对依托工程项目高边坡进行了基于期望成本的优化设计,优化结果验证了该成本模型的可行性。
关键词:高边坡;期望成本;生态成本;优化设计;边坡可靠度
在道路工程建设过程中,由于受到地形的影响,高边坡的出现往往难以避免,如何设计出兼顾了安全性和经济性的最优边坡坡型是一个重要的问题。已有的文献从不同的角度对边坡进行了稳定性分析和优化设计[1-3],但是这些研究几乎没有考虑不同的设计坡型对工程成本的影响。现有的基于高边坡期望成本的边坡设计优化模型只考虑了高边坡的开挖成本和失效后的治理成本,没有考虑高边坡建设带来的生态成本即环境损失成本[4-5]。在当今人们生态环保意识逐渐提高的情况下,高边坡的开挖对环境的破坏已经不能忽视。
1建立高边坡期望成本数学模型
高边坡综合治理的期望成本数学模型由目标函数和外部约束条件构成。
1.1期望成本的目标函数
本文研究的目标函数是高边坡建设的总期望成本费用。依据高边坡工程的建设过程,本文确定期望成本应该包括土方挖运成本、坡面防护成本、边坡可能失效时的治理成本、边坡失效带来的额外损失以及边坡开挖导致的生态破坏成本五个方面。
图1所示为典型高边坡的计算图式。
图示边坡共有n级,总坡高为H,综合坡角θ,单级坡高h、坡角α,平台的宽度l。土方挖运综合单价A,坡面防护的单价B,边坡破坏概率记为Pf,拟合的原始坡面线方程f(x),边坡破坏的滑动面方程g(x),高边坡总期望成本费用为C。

图1 高边坡计算模型示意图
因为路基占地面积和挖方量不随边坡形式改变而改变,所以本文计算相关占地面积和土方量时只考虑从坡角开始的边坡占地面积和挖方量,在沿坡长方向上按单位长度计算。
(1) 边坡开挖施工费C1等于挖方量乘以土方挖运综合单价,按(1)式计算,即
(1)
(2) 边坡开挖之后需要进行绿化防护,坡面防护费用等于面积乘以坡面防护单价,按(2)式计算,即
(2)
(3) 边坡破坏时修复处理费C3包括处理坍塌土方的费用和修复坡面的费用两个部分。处理土方费用等于土方量乘以土方挖运单价,修复坡面的费用等于面积乘以坡面修复单价,按(3)式计算,即
(3)
(4) 高边坡破坏风险损失费C4表示由于边坡破坏带来的其它额外损失,如阻塞交通等。本文采用损失系数法对该额外损失作出估计。依据文献[5]的研究结果,本文取损失系数λ=10,风险损失费按(4)式计算,即
(4)
(5) 高边坡建设的生态成本C5采用生物量因子控制法,按(5)式计算,即
C5=ECc∑Ai+∑Si·Cz=
(5)
其中,E是边坡所在地植被相对于森林的生物量因子值;∑Ai是边坡破坏原植被面积之和;∑Si是征地面积;Cc是单位面积森林的环境价值量;Cz是征地单价,由当地政府的政策决定。
在上面所列的公式中,ΔV表示的是设计坡面以下土体的总体积,表达式经过推导如下(在沿坡长方向上以单位宽度计算):
(6)
综合以上各点,高边坡建设总期望成本为
(7)
1.2求解成本目标函数的外部约束条件
对建立的高边坡期望成本目标函数求最优解时,需要根据实际情况对目标函数施加一定的外部约束,从而使得到的设计变量切实可行。
(1) 高边坡安全性约束。高边坡工程设计首先需要保证安全性,目前并没有统一的国家标准对边坡的可靠度进行规定。因此,本文仍按照文献[6]的要求采用安全约束为安全系数Fs≥1.25。
本文采用经典极限平衡法中的瑞典条分法计算边坡的安全系数,图2为瑞典条分法求解边坡安全系数的计算图。图中bi表示分析土条i的宽度,Pi、Pi+1表示土条i左右两侧所受正应力,Hi、Hi+1表示土条i左右两侧所受切应力,Ni表示土条i底部所受正应力,Ti表示土条i底部所受切应力。
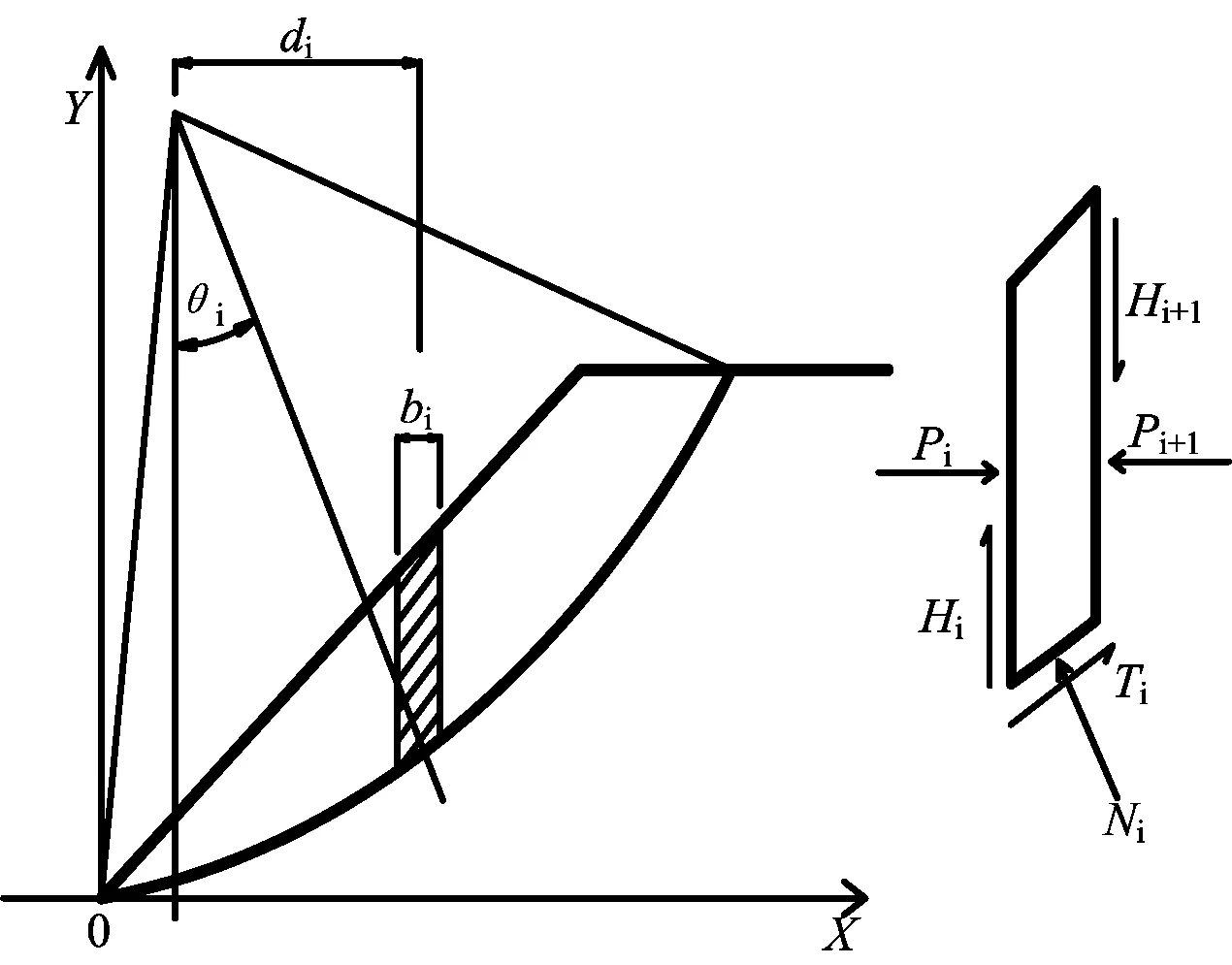
图2 瑞典条分法计算图示
瑞典条分法计算边坡安全系数Fs的公式为[7]
(8)
其中,Wi是第i个土条的重量;li是第i个土条底面的弧长;ci是第i个土条的土体粘聚力;φ是土体内摩擦角;θi是第i个土条底部中点与经过滑动面圆弧圆心的竖直线的夹角。
确定边坡危险滑动面就是要找到使安全系数值最小的那个面。由于瑞典条分法将潜在滑动面假设为圆弧形,那么寻找滑动面也就转化为寻找一组圆心坐标值(x0,y0)和圆弧半径值R使安全系数最小[8]。本文以此为思路,编制了在MATLAB平台上计算边坡安全系数的运算程序,然后再利用MATLAB自带的psearchtool工具箱自动搜索边坡最危险滑动面,同时给出边坡安全系数值。
得到高边坡潜在滑动面的圆心坐标值(x0,y0)和圆弧半径值R后,高边坡的滑动面方程即为
(9)
本文采用改进的一次二阶矩法(即验算点法),把土体内摩擦角φ、土体重度γ和土体粘聚力c视为随机变量,计算土质边坡的可靠度。在具体计算时,将可靠度计算过程编制为基于MATLAB平台的计算程序,经过迭代得到各个坡角条件下边坡的可靠度指标β,进而求得边坡的破坏概率[9],即
(10)
(2) 单级坡角和综合坡角的约束。根据大量已建成的类似于依托工程岩土体性质的高边坡工程,确定单级坡角α和综合坡角θ的约束范围为

(11)
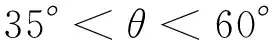
(12)
(3) 平台宽度的约束。许多工程实际已经说明,对于类似依托工程的高边坡取2 m宽的平台可以有效地改变坡脚处的应力集中,同时可以给边坡上相关的施工提供方便的工作平台。
由高边坡期望成本目标函数加上外部约束条件即可得到高边坡期望成本数学模型。
1.3确定高边坡建设的生态成本价值
生态成本的概念是对人类工程建设造成的环境价值损失的一种量化。生态环境系统价值的量化、货币化是比较困难的。本文参照矿山建设领域的研究,将生态成本分为征地成本和环境损失两个部分。征地单价由当地政府的政策决定,环境损失成本依据在资源环境研究领域有较大影响力的Costanza、谢高地等学者的研究成果[10-12]确定。
Costanza、谢高地等学者将生态系统价值类型进行了划分,然后对各种价值类型与农田的食物生产价值做对比,以农田的食物生产的生态服务价值为1,确定不同生物服务系统的价值当量因子,进而确定生态价值量。
文献[12]中分别给出了森林、草地、湖泊、湿地等不同生态系统类型在2007年单位面积生态价值当量。为了考虑通胀的影响,本文在计算时将文献中给出的价值乘以近些年中国居民消费价格指数(CPI),使其符合近些年价值量的增长。
2高边坡期望成本模型的求解
本文对该数学模型的求解主要是通过在MATLAB工作平台上编制程序实现的。程序分为几个子块,parameters块输入土体力学参数、坡高、坡面方程等参数,sliding块依据瑞典条分法自动搜索出危险滑动面并给出安全系数值,reliability块依据验算点法计算了边坡的可靠度,给出了边坡破坏概率,cost块计算了各坡角条件下边坡的期望成本值。计算过程如图3所示。

图3 模型求解过程图
3工程实例验证
本文选取了在建的安庆望东长江大桥项目接线工程第四标段的一段高边坡,利用该期望成本模型进行优化验证,该段高边坡总长约320 m,桩号为15 km+550 m~15 km+870 m,最大挖方高度为30m。根据实地调查并结合该处地质勘探报告,该处边坡地层主要为黏土、强风化灰岩、中风化灰岩,边坡整体呈土岩质边坡。本路段各地基岩土层力学性能指标推荐值如表1所列。

表1 边坡设计参数推荐值
依据各土层计算高度确定各个土层参数的计算权值,得出该处高边坡计算参数取值为:容重γ=22.64 kN/m3,粘聚力c=88.2 kPa,内摩擦角φ=28.20°。室内土工试验统计结果显示三个土体参数的标准差分别为:σφ=12°,σγ=2.33 kN/m3,σc=14 kPa。依据实测数据值,在MATLAB工作平台上拟合出该处高边坡原始地面线方程f(x)=0.003 571x2+0.618 6x+6.743。
按照文献[13]确定的土方和坡面治理定额的计算方法、《安徽省人民政府关于调整安徽省征地补偿标准的通知》(皖政[2015] 24号) 规定的征地单价、文献[10]中给出的生态单价,结合工程周围环境的具体情况,确定各项成本的单价,见表2所列。

表2 边坡各项成本单价取值
本文分别考虑了当设计为四级坡,即单级坡高为8 m+8 m+8 m+6 m,以及设计为三级坡,即单级坡高为10 m+10 m+10 m两种情况,按照该模型计算结果如表3所列。
表3列出了总坡角在35°到45°之间的计算结果,显示了两种情况下该处高边坡均在总坡角为39°时的期望成本最小,但是四级坡比三级坡的期望成本少了近1 000元,说明该处高边坡从期望成本的角度来说最佳设计总坡角为39°,采用四级坡的设计方案。值得注意的是,这里得到的期望成本并不等于实际时的施工成本,它包含了边坡破坏时的风险成本以及生态破坏成本。
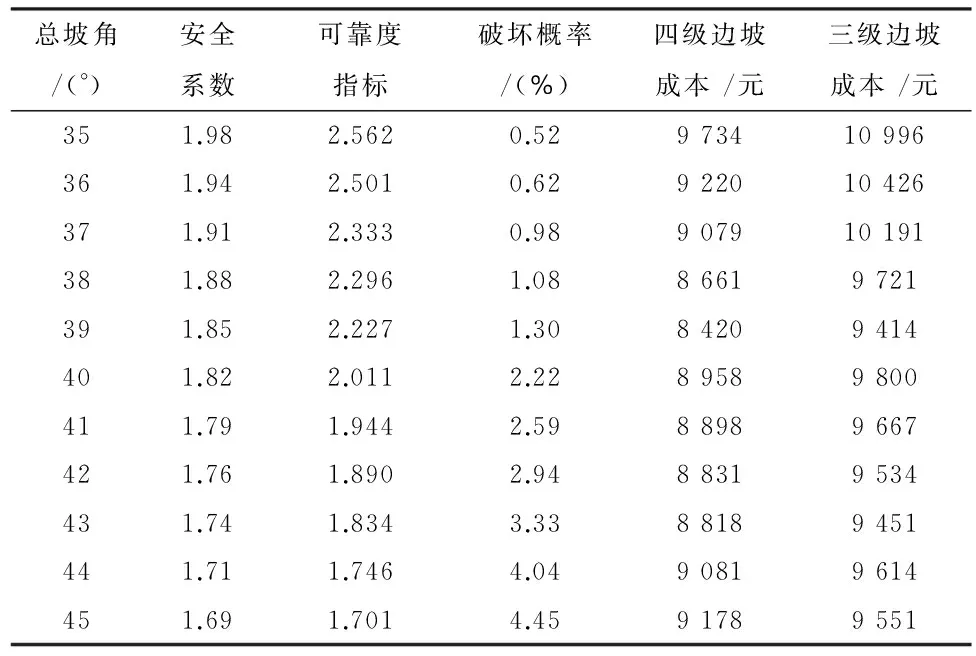
表3 高边坡成本计算值
4结束语
(1) 本文提出了一种计算高边坡综合治理期望成本的数学模型,运用该模型可以为高边坡的优化设计提供了一种新的设计思路。
(2) 在本文的高边坡期望成本模型的研究中引入了生态成本,参照矿山建设对环境影响的研究成果,将生态成本分为征地成本和环境破坏损失成本。在当今环保要求越来越高的背景下,边坡工程建设带来的自然生态的破坏、如何最大程度上协调边坡工程建设与环境保护的关系,这些问题都应该在设计时加以考虑。
(3) 运用该期望成本模型对望东大桥项目高边坡进行了优化设计,得到了期望成本最小时的设计坡型,验证了该成本模型的适用性。
〔参考文献〕
[1]沈金瑞,林杭.岩质高边坡开挖优化及稳定性分析的复合方法[J].东华理工大学学报(自然科学版),2009,32(4):350-356.
[2]蔡美峰,朱青山,乔兰,等.大顶铁矿露天采场边坡稳定性分析与优化设计[J].北京科技大学学报,2012,34(3):239-245.
[3]林杭,钟文文,熊威,等.锚杆长度与边坡坡率对最优锚固角的影响[J].岩土工程学报,2014,32(S2):7-11.
[4]刘小强,周世良,尚明芳,等.基于期望造价的高边坡优化设计及工程应用[J].水运工程,2011(12):25-29.
[5]叶万军,折学森,陈志新,等.基于可靠度理论的黄土高边坡优化设计[J].地球科学与环境学报,2005,27(2):82-85.
[6]JTG D30-2015,公路路基设计规范[S].
[7]顾晓薇,胥孝川,王青,等.矿山开采的生态成本[J].东北大学学报(自然科学版),2013,34(4):594-597.
[8]陈祖煜.土质边坡稳定性分析[M].北京:中国水利水电出版社,2003.
[9]胡松波.基于经济风险分析的公路土质边坡设计方法研究与应用[D].赣州:南华大学,2007.
[10]岩小明.基于可靠度理论的露天矿边坡风险分析[D].长沙:中南大学,2013.
[11]Costanza,d'ArgeR,deGrootR.The value of the world's ecosystem services and nature[J].Nature,1997,387:253-260.
[12]谢高地,甄霖,鲁春霞,等.一个基于专家知识的生态系统服务价值化方法[J].自然资源学报,2008,23(5):911-919.
[13]JTG/T B06-02-2007,公路工程预算定额[S].
收稿日期:2016-01-15
基金项目:安徽省高速公路控股集团科研项目(皖高科[2013]6号)
作者简介:杨敏(1991-),男,安徽肥东人,合肥工业大学硕士生;方诗圣(1962-),男,安徽岳西人,博士,合肥工业大学教授.
中图分类号:U416.1
文献标识码:A
文章编号:1673-5781(2016)01-0005-04
