粘弹性药柱泊松比的实验研究

李驭骉，李海滨

（内蒙古工业大学理学院，呼和浩特 010051）



粘弹性药柱泊松比的实验研究

李驭骉，李海滨

（内蒙古工业大学理学院，呼和浩特 010051）

摘要：泊松比作为材料的基本参数，对结构的力学性能有着重要影响。粘弹性材料的泊松比与线弹性材料相比，具有在时域或频域下为变量的特点。为了研究固体火箭发动机粘弹性药柱的泊松比，本文结合理论推导与试验测量，得到粘弹性材料泊松比在时域下的表达式。结合拉普拉斯变换和各向同性理论，利用粘弹性材料基本理论得到时域下的积分型表达式，最终将粘弹性材料的泊松比以Prony级数形式表达。通过试验得到材料相应的参数，并利用MATLAB软件对数据进行拟合和计算，最终得到粘弹性材料泊松比的实际函数，为固体火箭整体分析提供了相应参数。

关键词：泊松比；粘弹性；蠕变；固体推进剂

0　引言

泊松比是材料基本参数之一，因此泊松比的测量有着很重要的意义。线弹性材料在受力情况下横向应变和纵向应变的比值是一个常数，由此它的泊松比即为常数。但在粘弹性材料中，泊松比是与作用时间或频率和温度有关的变量参数［1-2］。并且大多数粘弹性材料满足各向同性，因此在泊松比的推导中可利用各类模量结合得到最终结果［3］。粘弹性材料在测量泊松比时不能应用弹性力学模量和应变之间简单的关系来求，需要通过拉氏变换求出相应的积分关系［4］。在本文中应用了拉伸松弛模量、剪切蠕变柔量在拉氏域中的变换最终推导出泊松比的积分表达式。

1　理论分析

粘弹性材料的力学行为介于弹性胡可定律和粘性牛顿理论之间，并且粘弹性的力学行为大多由单轴拉伸和剪切试验得出；其中蠕变，应力松弛（此后简称松弛）和正弦变化的动载荷比较常见［5］。

1.1粘弹性基本理论

在恒定载荷（或应力）作用下，应变随时间逐渐增加的过程叫做蠕变［6］。并且应变与恒定的应力的比值叫做蠕变柔量，D（t）。

在恒定应变下应力随时间而减小的过程叫做应力松弛［6］。并且应力与恒定的应变比值叫做松弛模量，E（t）。

上述公式（1）和（2）中都可以将定值用阶跃函数表示，H（t）。例如蠕变中，σ（t）=σ0H（ t ）。利用玻尔兹曼叠加原理，可得到：

同理松弛中可得到：

1.2时域下的泊松比

粘弹性泊松比在求解时需要应用相应理论，其中有微分型和积分型两种。力学模型和载荷历史决定了泊松比具体表达式；微分型由于不同的形式所得出的表达式不同，因此表达式不能统一，并且在拉式逆运算时计算复杂；与之相对的积分型就具有很大的优势［7-10］；既本文中利用积分型求解。

泊松比在时域下可以表示为：

其中εx（t）为横向应变，εy（t）为纵向应变。粘弹性材料在纵向单向受力的情况下，横向上的响应滞后于纵向变形历史。因此在求粘弹性材料的泊松比时不能直接用横纵应变的比值来求，需要在拉氏域进行运算后得出相应的计算公式。

在拉氏域中泊松比表达式转换为式（6）。

当进行蠕变试验时：

粘弹性材料在时域下具有各向同性，因此它满足弹性力学中泊松比μ与拉伸模量E、剪切模量G、剪切柔量J、体积模量K、体积柔量B的关系，如下式（9）-（11）。

根据弹性和粘弹性对应原理，利用拉普拉斯变换可得式（12）-（14）［7］。

对式（12）中进行拉氏逆变换得：

对式（13）中进行拉氏逆变换得：

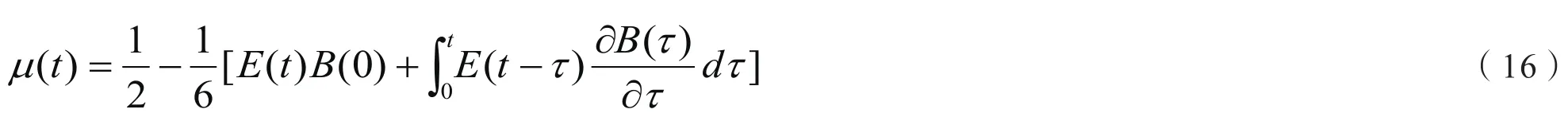
对式（14）中进行拉氏逆变换得：

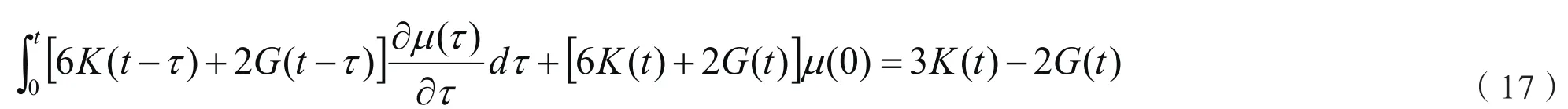
由式（15）-（17）可得泊松比的计算中，当得到拉伸松弛模量E（t）、剪切蠕变柔量J（t）、剪切松弛模量G（t）、体积蠕变柔量B（t）、体积松弛模量K（t）就可以推导出粘弹性材料的泊松比µ（t）。本文中应用的是公式（15），因此需要求E（t）和J（t）。

2　试验过程

2.1试验样品和设备

试样来源于某型号固体火箭发动机药柱。根据试验台对试样尺寸的特殊要求将拉伸试样加工为高50.00mm、宽11.00mm、厚度为3.60mm；剪切试样为高10.00mm、宽10.00mm、厚度为3.60mm的试样；拉伸试样如图1所示。

在实际加工中，试样的尺寸和设计尺寸存在差异，为了保证试验结果的准确性，在计算中都采用形状的真实尺寸。拉伸和剪切试样各制作5个。具体尺寸如表1。

图1　拉伸试样Fig. 1 Tension Specimen

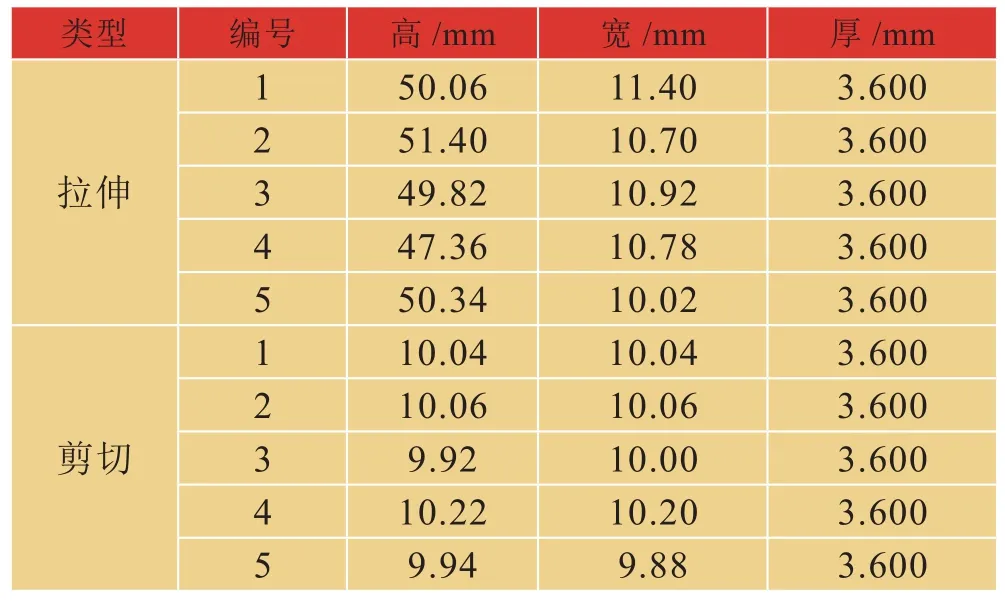
表1　试样尺寸Tab.1 Sample Size

为了减少试样加工对实验结果的影响，试样加工完成后在高温环境中（50℃）存放24小时，消除加工时产生的残余应力。

试验中总共应用两种器材；德国GABO公司生产的EPLEXOR动态力学热分析仪。其中动态力学热分析仪对试样进行蠕变和松弛试验，并测得纵向上的相应参数，如图2。两种试验台获得的数据精度都在小数点后6位以上，完全满足试验所需精度。

2.2试验过程与数据处理

总共做两组试验；其中每组用不同的试样重复做五次，除去异常数据后求均值。两组试验分别为拉伸松弛（图3）和剪切蠕变（图4）。在进行试验时保持试验过程恒温，控制在室温27℃。

图2　试验设备Fig. 2 Test Equipment

图3　拉伸试验Fig. 3 Tension Test

图4　剪切试验Fig. 4 Shear Test

上述两种试验分别得到了松弛模量E（t）和剪切蠕变柔量J（t）。得到的试验数据需要排除异常数据，在取舍时应用格拉布斯准则判断（设置信度α=95%）［11］；将异常数据删除得到最终数值。

3　结果处理

将试验中测得将拉伸松弛模量E（t）和剪切蠕变柔量J（t），通过MATLAB模拟成9阶Prony级数的函数；E（t）拟合的结果如图5。

应用MATLAB中函数拟合中存在的误差对计算泊松比有很大影响；因此在函数拟合时应将拟合精度提高，保证所得到的函数与真实值的误差足够小；并且在函数拟合时保证系数准确性。

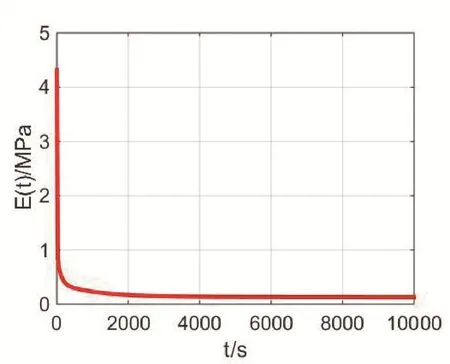
图5　松弛模量Fig. 5 Relaxation Modulus

其中E（t）公式为：

参数见表2：

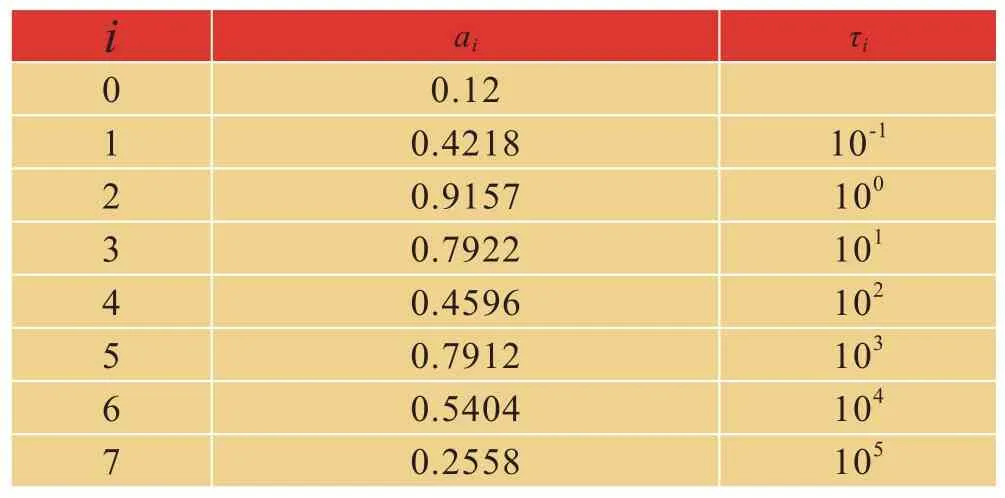
表2　松弛模拟参数Tab.2 Relaxation Modulus Parameter

将模拟出的E（t）和J（t）结果带入上述理论推导得出计算泊松比的公式（15）中得到泊松比函数µ（t），如图6。

最终也利用7阶Prony级数的模拟成式（21），参数见表3。

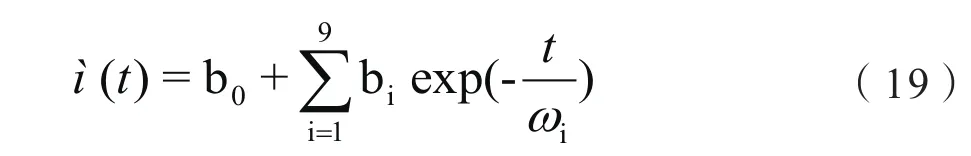
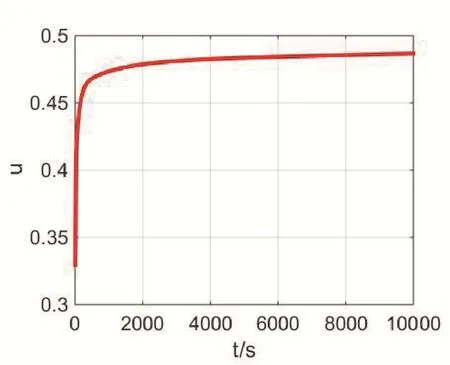
图6　泊松比拟合结果Fig. 6 Poisson's Ratio Fitting Result

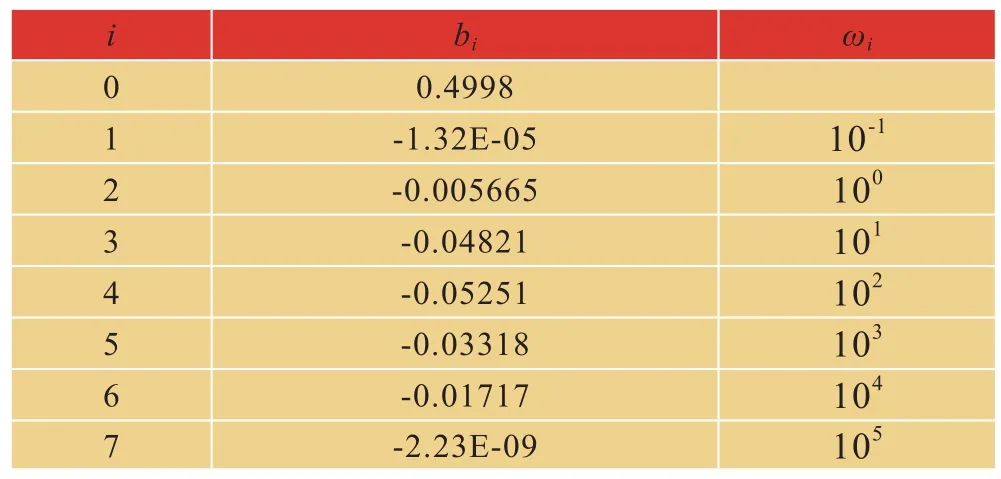
表3　泊松比参数Tab.3 Poisson's Ratio Parameter

4　结论

在药柱的粘弹性分析中泊松比的恒定假设已被普及使用；在研究中设为0.49左右［12］。由图（6）可见，在时间历程下，泊松比的变化只有在前期变化幅度很大。因此在粘弹性的力学分析中，这种对泊松比近似成常数的方法对最终结果产生的误差结果在初期影响较为明显，在后期则可以认定这种假设是允许的。并且通过本文最终得到结果可得出药柱泊松比随时间变化逐渐增大并趋近于0.5。

由于各个试验的时间历程都是104s，因此最终结果在104s以内的数据都为真实数据；在104s后的数据为估算数据。虽然在得到的结果在104s后仍然符合客观规律，但和实际值之间存在的差异暂时无法获得。

由于测量方法的制约不能进行变温测量，因此泊松比在温度变化下的规律仍然无法得到。粘弹性材料的泊松比是否存在时温等效原理也需要进一步的研究。

参考文献

［1］Lee H.S.，Jaeseung K.. Determination of viscoelastic poisson’s ratio and creep compliance from the indirect tension test［J］. Journal of Materials in Civil Engineering，2009，21（8）：416-425.

［2］Hilton H.H.，Yi S.. Significance of （an） isotropic viscoelastic Poisson ratio stress and time dependencies［J］. International Journal of Solids and Structures，1998，35（23）：3081-3095.

［3］Hilton H. H.. Implications and constraints of time-independent Poisson ratios in linear isotropic and anisotropic viscoelasticity［J］. Journal of Elasticity，2001，63（3）：221-251.

［4］Lakes R. S.，Wineman A.. On poisson’s ratio in linearly viscoelastic solids［J］. Journal of Elasticity，2006，85（1）：45-63.

［5］Klompen E.T.J.，Govaert L.E.. Nonlinear viscoelastic behaviour of thermorheologically complex materials. A modelling approach［J］. Mechanics Time-Dependent Materials，1999，3（1）：49-69.

［6］杨挺青，罗文波，等.黏弹性理论与应用［M］.湖北：科技出版社，2004. Yang Ting-qing，Luo Wen-bo，et al. Theory and application of viscoelastic［M］. Hubei： Science Press，2004.

［7］赵伯华.粘弹性泊松比与动态复数泊松比的研究［J］.推进技术，1995，16（3）：1-7. Zhao Bo-hua. An Investigation on Viscoelastic Poisson’s Ratio and Dynamic Complex Possion’s Ratio ［J］. Journal of Propulsion Technology，1995，16（3）： 1-7.

［8］Kassem E.，Grasley Z.C.，et al. Viscoelastic poisson’s ratio of asphalt mixtures［J］. International Journal of Geomechanics，2013，13 （2）：162-169.

［9］Keramat A.，Kolahi A.G.，Ahmadi A.. Waterhammer modelling of viscoelastic pipes with a time-dependent Poisson’s ratio［J］. Journal of Fluids and Structures，2013，43：164-178.

［10］Tschoegl N.W.，Knauss W.G.，et al. Poisson’s ratio in linear viscoelasticity a critical review［J］.Mechanics Time-Dependent Materials，2002，6（1）：3-51.

［11］Bar S.Y.，Lee X.. Estimation with Application to Tracking and Navigation［M］. New York：Wiley，2001.

［12］张海联，周建平.固体推进剂药柱泊松比随机粘弹性有限元分析［J］.推进技术，2001，22（3）：245-249. Zhang Hai-lian，Zhou Jian-ping. Viscoelastic stochastic finite element simulation of solid propellant grain with random Poisson's ratio ［J］. Journal of Propulsion Technology，2001，22（3）： 245-249.

本文引用格式：李驭骉，李海滨.粘弹性药柱泊松比的实验研究［J］. 新型工业化，2016，6（4）：16-21.

Citation: LI Yu-biao， LI Hai-bin. Experimental Study on Poisson’s Ratio of Viscoelastic Grain［J］. The Journal of New Industrialization，2016，6（4）: 16-21.

Experimental Study on Poisson’s Ratio of Viscoelastic Grain

LI Yu-biao， LI Hai-bin
（College of Science， Inner Mongolia University of Technology， Hohhot 010050， China）

Abstract:As the basic parameters of the material， Poisson’s ratio has an important influence on the mechanical properties of the structure. Compared with elastic material， the viscoelastic material Poisson ratio is variable in the time domain or frequency domain. In order to study the Poisson’s ratio of solid rocket motor， the expressions of Poisson’s ratio in time domain are obtained based on the theoretical derivation and experimental measurement. Based on Laplasse transform and isotropic theory，the integral expressions in time domain are obtained by using the basic theory of viscoelastic materials， and the Poisson’s ratio of viscoelastic materials is expressed by Prony series. Material’s corresponding parameters are obtained through the experiment，and experiment data is fit and calculated by using MATLAB software. Finally， gained actual function of viscoelastic material Poisson’s ratio， and provided corresponding parameters for the analysis of solid rocket.

Keywords:Poisson’s Ratio； Viscoelasticity； Creep； Solid Propellant

DOI：10.19335/j.cnki.2095-6649.2016.04.003

基金项目：国家自然科学基金（11262014）

作者简介：李驭骉（1990-），男，硕士，内蒙古工业大学理学院，主要研究方向：粘弹性材料研究；李海滨（1973-），男，教授，内蒙古工业大学理学院，主要研究方向：结构分析及优化计算，神经网络计算