颗粒级配与场地条件对滑坡运动特征的影响模型试验研究

冷晓玉，樊晓一

（西南科技大学土木工程与建筑学院，四川绵阳　621010）



颗粒级配与场地条件对滑坡运动特征的影响模型试验研究

冷晓玉，樊晓一

（西南科技大学土木工程与建筑学院，四川绵阳621010）

摘要本文运用滑坡模型试验研究了不同坡角和颗粒级配对滑坡运动的影响机制。试验结果表明：坡角对滑坡前缘具有显著的阻止作用，坡角越大，坡脚前后的速度差越大，能量损失越大；滑坡运动到坡脚后，呈现出持速运动特征，持速阶段的运动距离随坡角的增加而增加，但其平均运动速度则在坡角45°时达到最大值；滑坡运动过程分为明显的加速运动、持速运动和耗散减速运动3个阶段；在同一坡角条件下，中值粒径越大的岩土体经过坡脚作用后，阻止效应越不敏感，能量损失越少，能量传递的有效性越大，持速运动的距离越大。

关键词颗粒级配；场地条件；运动参数；滑坡

滑坡运动受多方面因素的影响。虽然已有的资料表明滑坡的运动受控于体积和高差所确定的总能量的大小。然而，对于总能量近似相等的个体滑坡而言，其运动结果可能有较大的差异。因此，国内外学者通过理论分析、模型试验、数值模拟等方法对滑坡做了大量研究。樊晓一等［1］对滑坡的等价摩擦系数、最大水平运动距离、最大垂直运动距离与滑坡体积的关系进行了分析，认为滑坡的运程不仅受体积的控制还与其诱发机制有关。潘欢迎等［2］通过物理模型试验测试了在不同滑体结构、坡角和初始速度组合下滑坡的运动过程，并分析了其基本规律。杜鹃等［3］考虑滑坡-碎屑流运动过程中滑体下表面的侵蚀作用和摩擦阻力变化，建立了基于有限积分法的计算模型。曾耀勋等［4］研究了坡脚及下垫面对滑体运动的减速机制。鲁晓兵等［5］重点考察了床面摩擦系数、土体内摩擦角、初始运动速度和坡角等因素对碎屑流运动形态的影响。郝明辉等［6］通过开展室内模型试验，研究了碎屑粒径、滑床糙率和挑坎对运动特性的影响。张龙等［7］采用PFC3D模拟鸡尾山滑坡在不同坡面摩擦系数和滑体粘结强度下的运动特征。Zhou等［8］运用离散元程序，研究不同的力学参数、滑坡体体积、地形条件对滑坡运动过程的影响。

这些研究或注重于滑坡启动机理的研究，或关注滑体本身运动特征的研究，或针对滑坡运动的规模效应研究，忽略或简化了场地条件对滑坡运动特征的影响，与实际的滑坡运动规律存在着较大的差异。然而滑坡失稳后的运动特征不仅受滑坡诱发机制、总能量的控制，还与场地条件有关，而滑坡运动特征又是滑坡灾害评估及防治的决定性因素［9-10］。因此，研究颗粒级配、场地条件对滑坡运动特征的作用机制，能够为滑坡的规划防治工作提供重要的理论依据。

1　滑坡物理模型试验

1. 1试验装置

模型装置主要由砂箱、滑道和支架3部分组成。砂箱是装载滑体的容器，砂箱前端设有挡板控制滑坡的启动，滑道是试验中滑体运动的主要场所。为便于滑坡运动速度的监测和计算，在滑道每隔10 cm划线标记。采用数码相机对试验中滑坡的运动停积过程进行拍摄，如图1。滑坡模型装置示意如图2。

图1　数码相机布置示意

图2　滑坡模型装置示意

1. 2试验材料及内容

在对典型滑坡堆积物现场调查的基础上，选择较为典型的高速滑坡体的颗粒粒组，同时考虑到试验仪器对于岩土体颗粒粒径d的限制条件（d≤60 mm），选择颗粒粒径范围为0. 25～50 mm，设计出如表1所示的3种岩土样，级配曲线如图3。配制好的岩土样如图4所示。

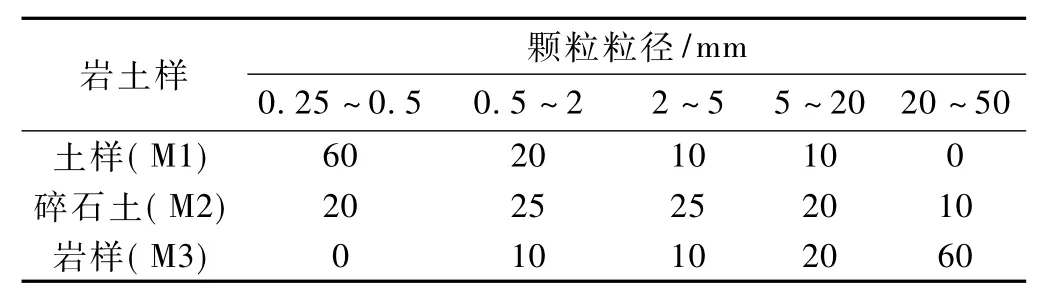
表1　岩土样级配组成

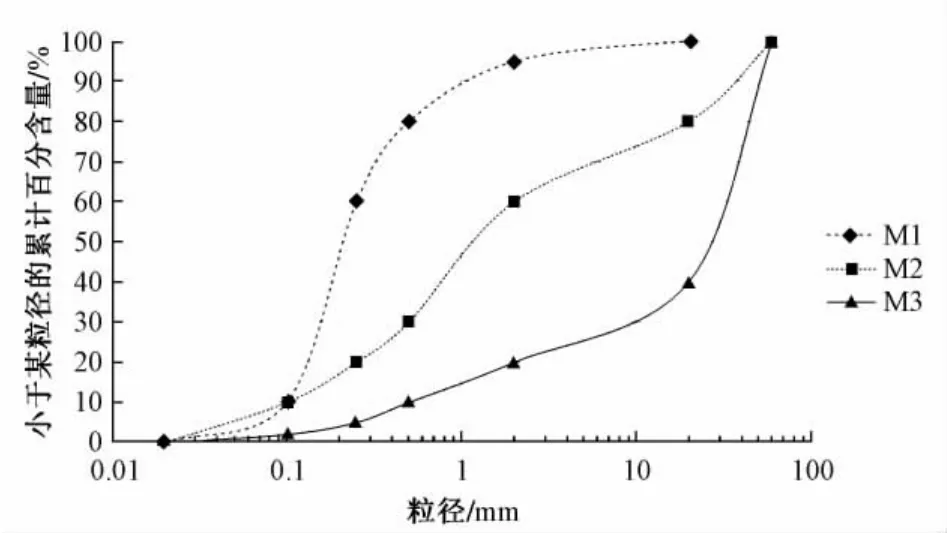
图3　岩土样级配曲线

图4　配制好的岩土样

坡脚型滑坡示意如图5。针对坡脚型滑坡不同滑体规模（0. 05，0. 10，0. 15，0. 20 m3）、不同颗粒级配（M1～M3）以及滑体在不同坡角α（α= 35°，45°和56°）下的运动性试验，研究滑坡规模、岩土体类型与场地条件的耦合作用对滑坡运动特征的影响。

图5　坡脚型滑坡示意

2　滑坡运动特征分析

2. 1坡角对滑坡运动特征的影响

碎石土滑坡在不同滑体体积下的速度分布曲线见图6。可以看出滑坡的运动阶段基本一致，即滑坡失稳后，在斜坡面迅速加速下滑，到达坡脚处时，滑体前缘速度达到最大。同一坡角的最大速度受滑体体积的影响很小，峰值速度基本一致，坡角56°时滑坡前缘最大速度接近6 m/s，坡角45°时滑坡前缘最大速度接近5. 5 m/s，而坡角35°时滑坡前缘最大速度为5 m/s，可见随着坡角的减小滑坡前缘能达到的最大速度减小。这是因为随着坡角的减小，斜坡坡长增加，在斜坡上受摩擦所损耗的能量也随之增加，致使滑体到达坡脚处的最大速度减小。

滑体体积为0. 15 m3的岩质滑坡在不同坡角下的速度分布曲线见图7。从图可见，经过坡脚作用后坡角45°时速度波动幅度和持续时间最大，由此引起的碰撞和能量传递最为剧烈。滑体前缘启动后加速下滑至坡脚，经过坡脚作用后速度突变，开始骤减，接着会出现一定程度的速度回弹。其原因是后缘滑体给前缘滑体传递能量，使得速度得到部分恢复。随着滑体继续运动，滑体中部经过坡脚作用，中部滑体对前缘滑体的能量传递作用大大减弱，前缘滑体的速度则出现再次下降。后部滑体继续运动传递能量给中部，依次传递，故而前缘滑体的速度又出现上升。整个过程中发现中部速度剧减的时刻点恰好也是前部速度增加的时刻点，同时后部速度剧减点也恰好是中部速度呈持速运动的起始点，很好地验证了本文在进行滑坡试验分析中提出的能量传递规律。而碰撞引起的能量传递，使得前缘滑体接受到的能量与受摩擦损耗的能量基本一致，这是造成明显持速运动的主要原因。

分析速度峰值至最后静止这一段，发现坡角45°时水平运动距离达到极大值。这是因为坡角由56°改变至45°时，滑坡体在遭遇坡脚后，内部碰撞机会增多，撞击导致能量传递，后方滑体将能量不断传递给前缘滑体，致使滑坡前缘速度上下波动呈现出明显的持速特征。在运动过程中滑坡体之间的能量传递越为持久，持速特征表现得越加明显，滑坡所能达到的水平运动距离也就越大。当坡角由45°减小至35°时，碰撞机会增多的同时也会导致碰撞耗能增加，滑坡体在碰撞过程中因碰撞产生的能量损耗远大于其通过碰撞传递的能量，能量逐步耗散直至最终堆积于水平基底。同时，坡角的变小造成由规模效应引起的速度波动并不显著，即规模越大，坡脚后产生的速度差越小，持速阶段越不明显，水平运动距离越近。

2. 2滑体粒径级配和规模对滑坡运动特征的影响

根据滑坡前缘沿水平运动距离的速度分布曲线（图6），可以将整个滑坡运动过程分为启动加速、持速以及耗散减速3个阶段。启动加速阶段：滑坡体启动后，在斜坡坡面上加速下滑。持速阶段：滑体前缘经过坡脚位置后受到坡脚的约束阻挡作用，速度急剧减小又受到后缘滑体的碰撞，将能量继续传递，使前缘运动速度增加，并持续上下波动震荡。耗散减速阶段：滑体动能耗尽，停积在水平基底上。

坡角35°时不同岩土质滑坡的速度分布曲线见图8。可以观察到：在持速运动阶段的速度波动区间，速度剧减后再次达到的速度往往为后续阶段的最大值。这是因为此时受坡脚场地条件的约束，滑坡体内部的速度差达到最大，致使内部碰撞越加剧，滑坡前缘获得的能量也越多。同时可以得到在同等条件下，滑坡体碰撞导致的能量损耗从大到小为土质滑坡＞碎石土滑坡＞岩质滑坡，这也是在高速远程滑坡-碎屑流中岩质滑坡居多的原因之一［11］。

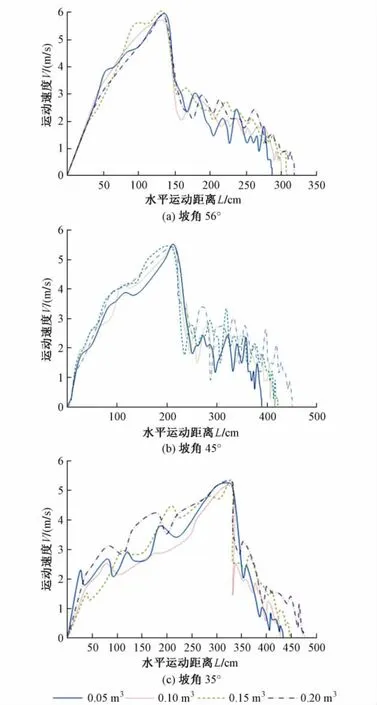
图6　碎石土滑坡在不同滑体体积下的速度分布曲线

图7　岩质滑坡在不同坡角下的速度分布曲线

另外，在同一坡角条件下滑坡规模的改变也造成滑坡前缘在持速平衡阶段初始速度峰值有所不同。总的来说，规模越大，在同一时间运动到坡脚处的滑体量越多，滑坡前缘在持速阶段的初始速度峰值也越大，导致滑体内部碰撞越为频繁，前缘受到的碰撞传递能量也就越有效。由图8还可以看出：在同一坡度条件下，滑坡水平运动距离的远近取决于持速阶段水平运动距离的大小。

2. 3滑坡运动距离与粒径和规模的关系

不同岩土质滑坡运动距离与规模的关系拟合曲线见图9。可以看出不同岩土质滑坡规模与运动距离均呈幂指数关系，表达式为L = kVb（k为比例系数，b为指数因子），这符合滑坡运动的规模效应，即滑坡的规模越大，滑坡的运动距离越远。同时发现：当斜坡坡角a为35°时，b值的取值范围为0. 044 7～0. 071 1；当a 为45°时，b值的取值范围为0. 071 8～0. 099 2；而当a 为56°时，b值的取值范围为0. 084 5～0. 135 1。表明随着坡角的增加，滑坡规模对运动距离的影响十分显著。坡度越大，运动距离随滑坡规模的增大增加得越明显。

图8　坡角35°时不同岩土质滑坡的速度分布曲线

由图9还可以看出：岩土质滑坡运动距离与规模的关系拟合曲线反映出的规律变化极为符合滑坡的规模效应，但不同土体的相关系数有差异，说明滑坡体组成对运动特征也有一定的影响。相对而言，岩质滑坡以滚动为主，运动过程的摩擦系数较低；土质滑坡则主要以滑动为主，运动过程的摩擦系数较高；而碎石土滑坡则包含了在滑体上部的粗骨料滚动运动和滑体下部的细颗粒滑动运动两种运动方式，下部的细颗粒在滑道摩擦力的作用下运动较缓慢，这对上部的粗颗粒的运动产生一定的牵制。

图9　不同岩土质滑坡运动距离与规模的关系拟合曲线

不同颗粒组成的滑坡随坡角变化，b值也在发生变化。土质滑坡时，b值的取值范围为0. 044 7～0. 135 1；碎石土滑坡时，b值的取值范围为0. 059 4～0. 125 7；岩质滑坡时，b值的取值范围为0. 071 1～0. 084 5。表明随着粒径的减小，滑坡规模对运动距离的影响随坡度的改变更为敏感，这一结果也能从一定程度上解释土质滑坡的受灾范围与规模和倾角的关系尤为密切。对于岩质滑坡，滑坡规模对运动距离的影响随坡度的改变虽不敏感，但运动距离较碎石土滑坡和土质滑坡远。

3　结论

1）通过室内滑坡模型试验验证了滑坡在运动过程中，坡体内部之间相互碰撞产生能量传递现象，后部滑体通过撞击把能量传递给前缘滑体，自身失去能量而堆积于坡脚附近，而滑坡前缘受后部滑体撞击传递能量，导致其运动的距离较远。

2）对于坡脚型滑坡，滑坡体经过坡脚作用后持速阶段的历时长短是滑坡前缘运动距离远近的关键。在总能量一定的情况下，滑坡体经过45°的坡脚作用后，内部碰撞机会较35°，56°多，在运动过程中滑体之间的能量传递较持久，持速特征最明显，由此导致滑坡速度高峰后的运动距离最远。

3）随着坡角的增加，滑体受坡脚约束耗损的能量增加，导致滑体运程减小。但同时由于竖向速度增强，滑体撞击坡脚时产生的反作用力增大致使滑体迅速解体，内部碰撞加剧，引起能量传递集中，导致颗粒最大运动距离增加，这也是滑坡撞击解体呈碎屑流运动往往导致超长运程的原因。

参考文献

［1］樊晓一，乔建平，韩萌，等.灾难性地震和降雨滑坡体积与运动距离研究［J］.岩土力学，2012，33（10）：3051-3058.

［2］潘欢迎，柴波，李想.不同结构顺层岩质滑坡运动过程风险性的实验研究［J］.工程地质学报，2013，21（5）：788-796.

［3］杜鹃，殷坤龙，王佳佳.基于有限体积法的滑坡-碎屑流三维运动过程模拟分析［J］.岩石力学与工程学报，2015，34 （3）：480-488.

［4］曾耀勋，樊晓一，段晓冬.坡脚型场地对滑坡体运动的减速机制研究［J］.水土保持通报，2014，34（4）：193-196.

［5］鲁晓兵，张旭辉，崔鹏.碎屑流沿坡面运动的数值模拟［J］.岩土力学，2009，30（2）：524-527.

［6］郝明辉，许强，杨磊，等.滑坡-碎屑流物理模型试验及运动机制探讨［J］.岩土力学，2014，35（增1）：480-488.

［7］张龙，唐辉明，熊承仁，等.鸡尾山高速远程滑坡运动过程PFC3D模拟［J］.岩石力学与工程学报，2012，31（增1）：2601-2611.

［8］ZHOU Jiawen，HUANG Kangxin，SHI Chong，et al. Discrete Element Modeling of the Mass Movement and Loose Material Supplying the Gully Process of a Debris Avalanche in the Bayi Gully，Southwest China［J］. Journal of Asian Earth Sciences，2015（99）：95-111.

［9］樊晓一，乔建平.“坡”、“场”因素对大型滑坡运动特征的影响［J］.岩石力学与工程学报，2010，29（11）：2337-2347.

［10］MEUNIER P，HOVIUS N，HAINES J A. Topographic Site Effects and the Location of Earthquake Induced Landslides ［J］. Earth and Planetary Science Letters，2008（275）：221-232.

［11］ZHANG Ming，YIN Yueping. Dynamics，Mobility-controlling Factors and Transport Mechanisms of Rapid Long-runout Rock Avalanches in China［J］. Engineering Geology，2013（167）：37-58.

（责任审编葛全红）

Model Test Study on Influence of Gradation and Field Condition on Landslide Characteristics

LENG Xiaoyu，FAN Xiaoyi
（School of Civil Engineering and Architecture，Southwest University of Science and Technology，Mianyang Sichuan 621010，China）

AbstractIn this paper，the influences of slope and gradation on landslide movement were analyzed based on model test. T he test results show that the slope angle of landslide has an significant effect on the front edge of landslide. Larger slope angle leads to larger velocity difference before and behind the toe，and larger energy loss. T he velocity stays at a level while the landslide moves to the toe. T he distance at this stage increases with the slope angle，while the average velocity reaches its maximum at 45°slope angle. T he entire landslide includes three stages：accelerated movement，constant-speed movement and decelerated movement. Under the condition of the same angle，if the median diameter of grain is larger，the prevention from the toe and the loss of energy will be less，energy transfer will be more effective and the distance of constant-speed movement will be longer.

Key wordsGradation；Field condition；M ovement parameter；Landslide

中图分类号P642

文献标识码A

DOI：10. 3969 /j. issn. 1003-1995. 2016. 05. 31

文章编号：1003-1995（2016）05-0139-05

收稿日期：2016-01-10；修回日期：2016-03-20

基金项目：西南科技大学研究生创新基金（15ycx103）

作者简介：冷晓玉（1989—），女，硕士研究生。