HRB500级钢筋RPC简支梁挠度计算方法
2016-06-12马洪伟罗丽娜
付 强,马洪伟,罗丽娜
(桂林理工大学广西岩土力学与工程重点实验室,广西桂林 541004)
HRB500级钢筋RPC简支梁挠度计算方法
付强,马洪伟,罗丽娜
(桂林理工大学广西岩土力学与工程重点实验室,广西桂林541004)
摘要为了获得高强钢筋活性粉末混凝土简支梁受弯构件挠度的计算方法,进行了4根不同配筋率的高强钢筋活性粉末混凝土梁的结构试验。研究结果表明,试验梁的挠度实测值比普通钢筋混凝土梁计算公式计算值低16%左右。基于试验数据,在普通钢筋混凝土梁挠度计算式中引入挠度折减系数并取为0. 84,对公式予以修正,从而建立了高强钢筋RPC梁挠度的计算公式。公式计算值与试验值吻合良好。
关键词高强钢筋;活性粉末混凝土;RPC梁;挠度计算
活性粉末混凝土(Reactive Powder Concrete,简称RPC)是一种具有高韧性、高耐久性、超高抗折强度等优良性能的新型混凝土。HRB500高强钢筋具有延展性好、强度高、碳当量低、可焊性好和节省材料的优点,将两者结合在一起,有望形成一种新型的钢筋混凝土构件,具有更优良的物理力学性能。有关静定结构受弯构件的挠度计算,国内外学者已经进行了大量研究。文献[1]通过在高强混凝土中掺入钢纤维得出,掺入钢纤维有利于提高梁的刚度,减小给定荷载下的挠度;文献[2]通过对比RPC200受弯构件荷载-挠度曲线得出,RPC200的弯曲韧性比普通砂浆高数十倍;文献[3]通过试验得出活性粉末混凝土梁比普通混凝土梁有更强的刚度;文献[4]通过15根HRB500高强钢筋普通混凝土梁试验,建立了适合于HRB500高强钢筋普通混凝土梁挠度的计算方法。但是对于高强度的HRB500级钢筋和高性能的RPC这2种材料组成的新型混凝土材料受弯构件的挠度计算,目前尚无明确的计算方法。本文旨在通过试验研究,提出高强钢筋RPC简支梁的挠度计算公式,为加快RPC构件的工程应用提供参考数据。
1 试验设计
试验共设计制作了4根高强钢筋RPC简支梁,截面尺寸均为150 mm×250 mm,长度2 000 mm,跨度1 800 mm。采用三分点对称方式进行加载,如图1所示,试验梁设计参数见表1。RPC的配合比基于最大密实度理论[5]而设计,详见表2。
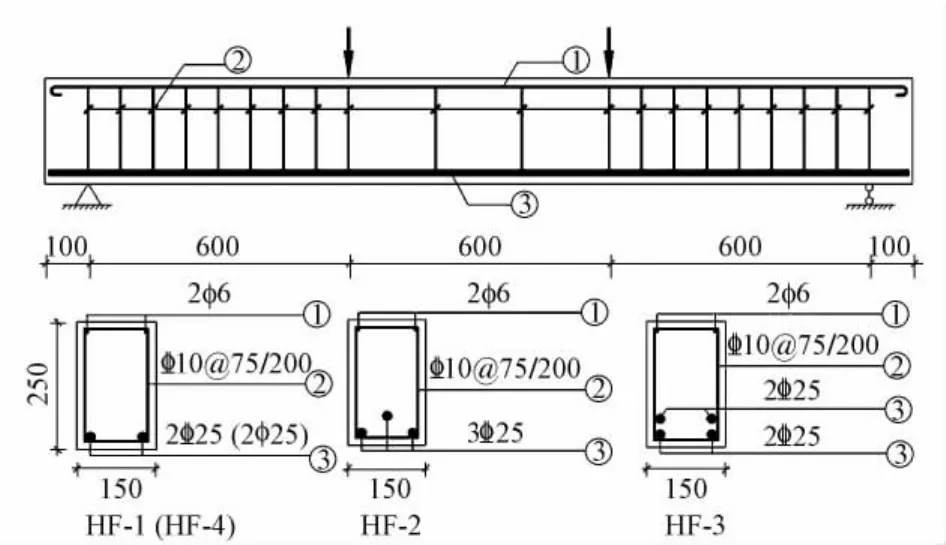
图1 梁配筋图及加载点(单位:mm)

表1 试验梁设计参数
2 试验结果及分析
2. 1试验现象
以试验梁HF-2为例,绘制平均应变沿截面高度的分布图,见图2。经过分析可以得出以下结论:试验梁都属于适筋受弯破坏;沿试验梁纯弯段截面不同高度上RPC的应变均符合平截面假定;破坏时受拉钢筋均达到屈服强度,受压区RPC被压碎。

表2 RPC质量配合比(钢纤维为体积比)
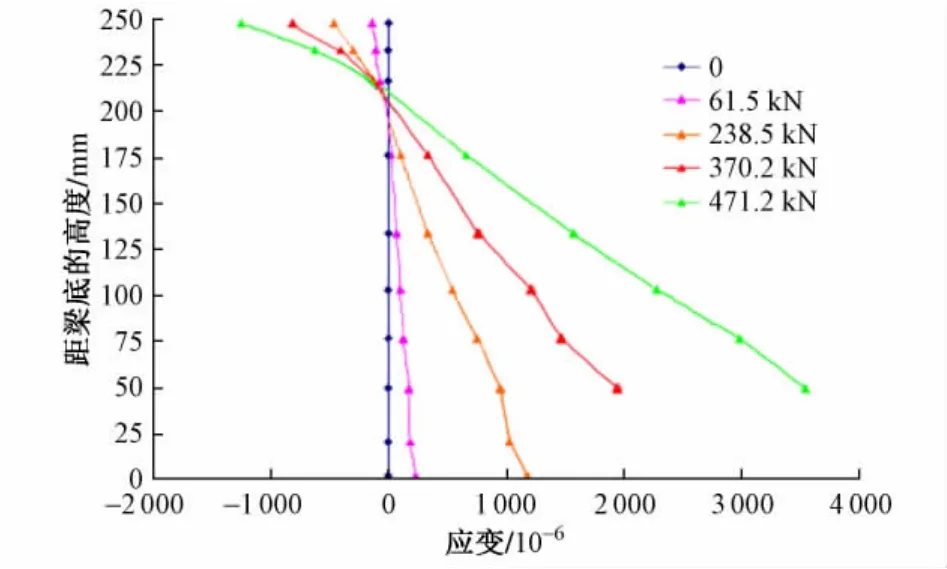
图2 试验梁平均应变沿截面高度分布示意
2. 2试验结果
2. 2. 1荷载-挠度分析
图3为试验梁荷载-跨中挠度关系曲线。
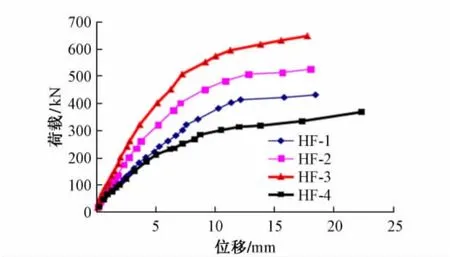
图3 试验梁荷载-跨中挠度关系曲线
由图3可知:
1)HF-1至HF-3的荷载-挠度曲线,随着配筋率的提高,相同荷载下的试验梁挠度值越来越小。说明配筋率的提高有利于加强梁的刚度,从而降低了挠度。
2)比对HF-1与HF-4的荷载-挠度曲线,同一荷载下,钢筋等级越高,梁的挠度越小。首先是HRB500级钢筋的握裹能力强于普通钢筋,钢筋拉应变不均匀系数较小,提高了梁的刚度,挠度减小;其次钢筋等级越高,其合力越大,RPC的受压区高度也越大,挠度越小。
3)荷载较小时,高强钢筋RPC梁处于弹性状态,每根梁的荷载-挠度曲线均为直线,抗弯刚度无明显变化。当施加荷载至受拉区边缘的RPC达到极限应变时,试验梁表面开始出现裂缝,试验梁的挠度逐渐增加,但幅度较小。随着荷载的继续增大,由于受拉刚化效应[6],荷载-挠度曲线出现第一个转折点之后继续上升,但斜率呈减小趋势且变化比较平缓。主要因为RPC梁中钢纤维的阻裂作用以及钢筋的销栓作用[7],使RPC与钢筋之间的粘结力提高,减缓了裂缝高度和宽度的增长,裂缝间纵向受拉钢筋重心处的拉应变不均匀系数ψ也相对较小。当加载到钢筋屈服时,试验梁的破坏模式均为顶部受压区混凝土被压碎,荷载-挠度曲线在破坏点发生转折,转折点的位置先后不一,说明受拉钢筋配筋率的变化,对于试验梁进入塑性阶段的进程有一定影响。继续增加荷载到临近破坏,曲线的斜率明显下降,曲线末端发展较平缓,近似水平。从纵向钢筋屈服到试验梁破坏的过程中荷载的增加幅度很小,而试验梁的变形却很大,表明高强钢筋RPC梁有良好的延性。
2. 2. 2挠度试验值与计算值对比分析
对于普通钢筋混凝土简支梁而言,正常使用极限状态下梁的挠度可按结构力学方法式(1)进行计算,以梁HF-2为例将试验数据代入后得到图4的结果。

式中:Bs为按《混凝土结构设计规范》(GB 50010—2010)[8]计算所得的短期刚度值,开裂前Bs= 0. 85EcI0,开裂后Bs=(EsAsh20)/(1. 5ψ+ 0. 2 + 6αEρ);α是与荷载的作用形式和约束条件有关的系数,对于承受集中对称荷载的简支梁,α= 0. 106 5;l0为试验梁跨度。
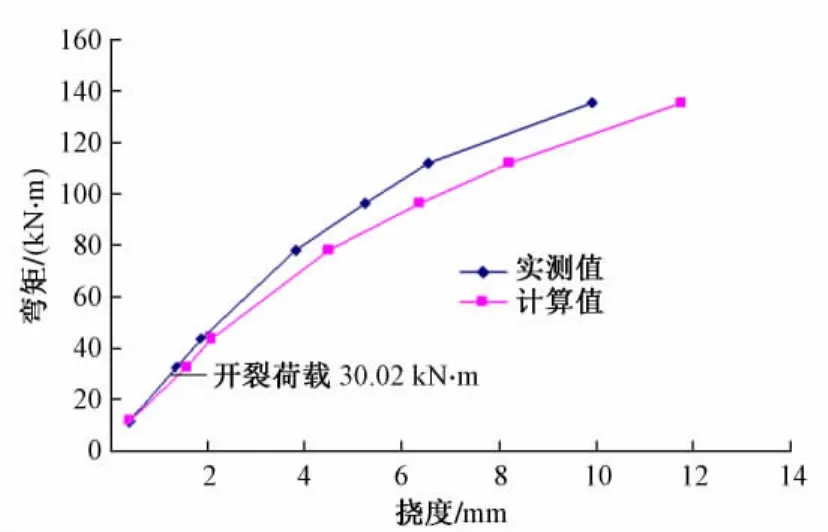
图4 挠度-弯矩关系曲线
从图4可以看出:试验梁开裂之前,按普通钢筋混凝土梁计算公式计算的挠度值与实测值的误差较小。但试验梁开裂之后,实测值和计算值误差则较大,实测值比计算值低16%左右。说明对于高强钢筋活性粉末混凝土受弯构件的挠度,不能简单套用普通钢筋混凝土挠度计算方法计算,必须进行修正。
3 挠度计算公式修正
3. 1建立修正公式
高强钢筋活性粉末混凝土与普通钢筋混凝土相比,具有更高的强度、韧性、耐久性等优良性能,去粗骨料、掺入活性掺合料,减少了RPC材料基体部分界面原始裂缝,所掺钢纤维等成分对梁裂缝的发展和挠度的增加有一定抑制作用,因此试验梁挠度实测值小于按普通钢筋混凝土梁计算公式求得的计算值。
试验梁截面一旦开裂,梁的刚度也随即发生变化,通常梁的挠度按照最小刚度原则计算。计算开裂后的挠度,关键在于确定构件截面的开裂刚度,截面开裂后刚度与开裂前的刚度相比有一定的折减。所以为进一步了解混凝土开裂后构件真实的刚度,本文通过试验梁跨中挠度的实测值反推跨中截面的抗弯刚度试验值Bexp,则

由Bs/Bexp可以得出计算刚度与实际刚度的相对关系,因为Bs/Bexp= ft/f0,4根RPC试验梁开裂后,将各级荷载作用下ft/f0与M /Mu的关系数据绘制成曲线,见图5。用一条二次曲线拟合得

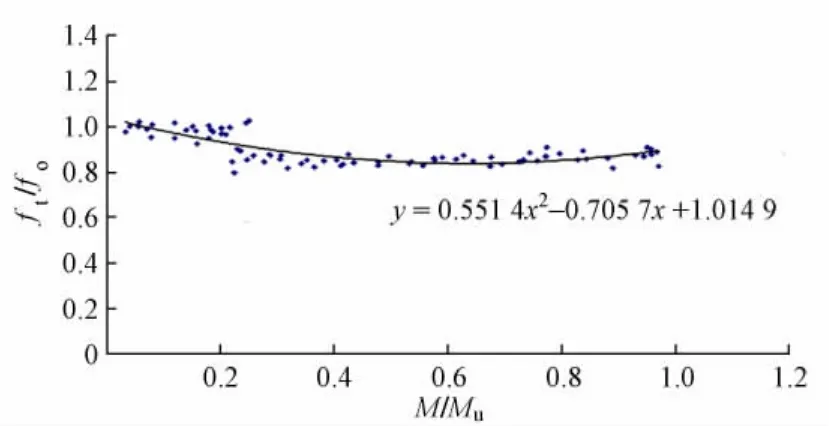
图5 试验梁ft/f0随M /Mu变化关系
由于短期刚度Bs的确定与钢筋应变不均匀系数等有关,对其调整需要做大量试验[9-11]。为简化考虑,本文根据试验结果,建议在原有挠度计算公式的基础上引入挠度折减系数η(令η= ft/f0),将高强钢筋活性粉末混凝土梁挠度计算公式修正为梁开裂后,钢筋及RPC中的钢纤维开始发挥作用,活性粉末混凝土及钢纤维的抗拉作用延缓了试验梁刚度的骤减,试验梁挠度与普通钢筋混凝土梁的挠度公式计算值相差较大。M =(0. 3~0. 9)Mu时,随着荷载的增大及裂缝的开展,试验梁的挠度折减系数η较为稳定,基本处于定值0. 84。原因在于活性粉末中的钢纤维在裂缝开展过程中具有减缓裂缝发展的作用,随着钢纤维的不断被拔出,试验梁的刚度也逐渐减小,并趋于定值。综上所述,相同条件下,高强钢筋活性粉末混凝土梁的挠度比普通钢筋混凝土梁偏小,建议乘上折减系数0. 84,与梁的实际变形状态相吻合。

从表3可看出,在M = 0. 2Mu之前试验梁挠度折减系数η维持在1. 0左右,此阶段试验梁还未开裂。M =(0. 2~0. 3)Mu时,试验梁的挠度折减系数η骤减。

表3 不同M /Mu下η取值
3. 2验算修正公式
将本文和文献[3]试验中的弯矩和挠度数据值分别代入式(4),此处η取0. 84,得到表4和表5。其中ft为实测挠度值;fc为按式(4)计算的挠度值。
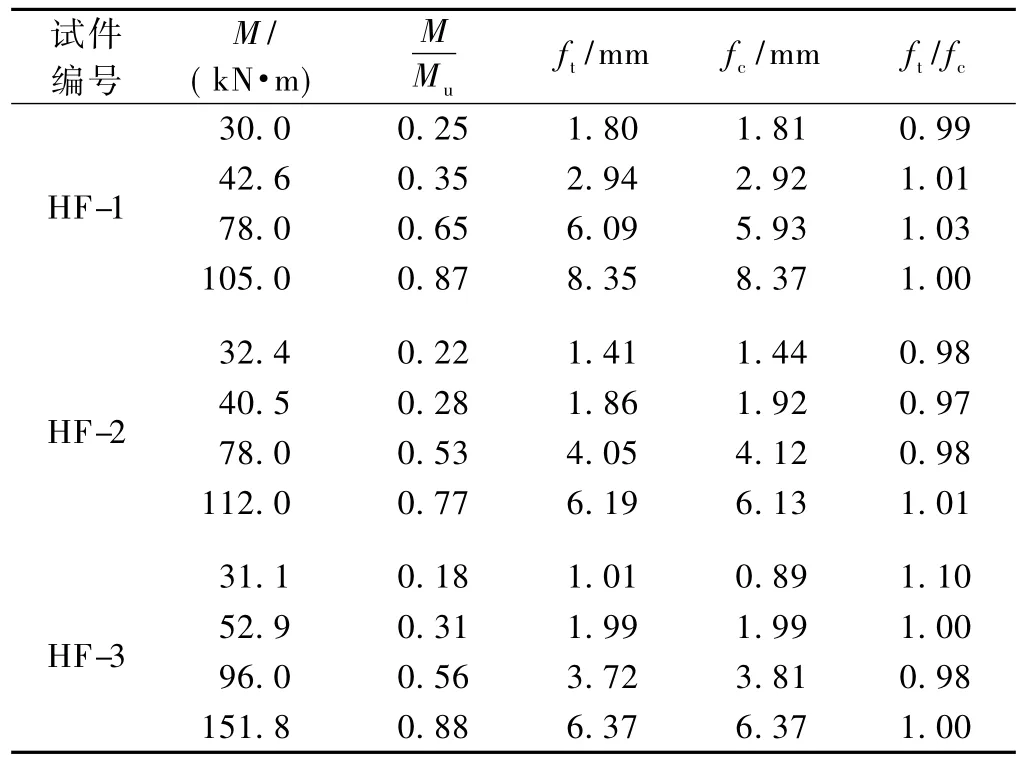
表4 试验梁式(4)计算值与实测值对比
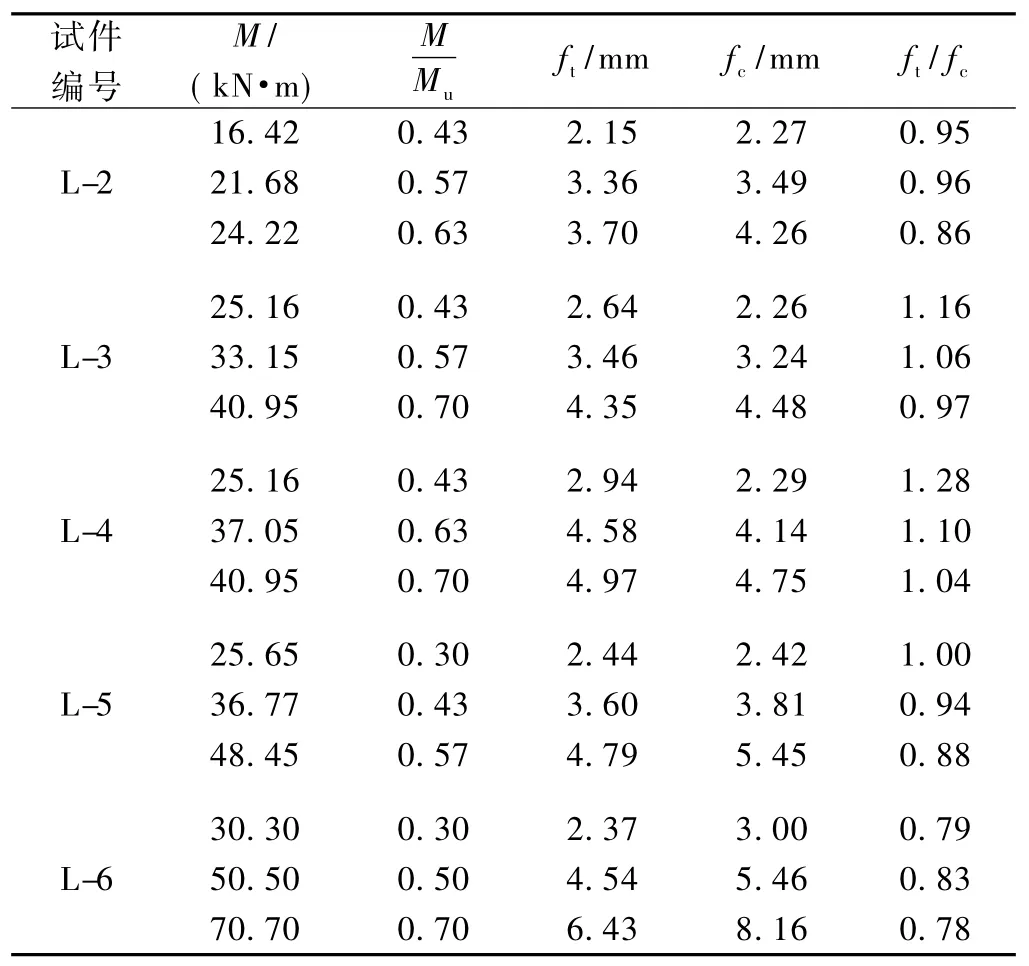
表5 文献[3]中式(4)计算值与实测值对比
表4中本文ft/ fc的平均值1. 01,标准差0. 035,变异系数0. 03;表5中文献[3]ft/ fc的平均值0. 98,标准差为0. 135,变异系数为0. 137。表4和表5中所有梁的ft/ fc的平均值0. 99,标准差0. 098,变异系数0. 099。除L-6的数值有一定的偏离外,其他梁的计算值和实测值比较吻合,说明式(4)有一定的实用性。
4 结论
1)高强钢筋RPC梁开裂前,由于RPC中的钢纤维还未发挥作用,对梁的刚度影响较小,仍然可按普通钢筋混凝土梁的挠度公式计算其挠度。
2)高强钢筋RPC梁开裂后的挠度实测值比规范计算值低16%左右。在普通钢筋混凝土梁挠度公式的基础上,引入挠度折减系数η= 0. 84进行修正,建立公式(4),其挠度计算值与试验值吻合良好,可以为高强钢筋RPC梁的挠度计算方法提供参考。
3)公式(4)是以本试验为基础所得,所求挠度为短期荷载下高强钢筋RPC梁的变形,未考虑长期荷载影响。徐变也会导致梁的挠度增大,因此,高强钢筋RPC梁在长期荷载作用下的挠度计算还需要进一步试验研究和理论分析。
参考文献
[1]ASHOUR S A,WAFA F F. Flexural Behavior of High-strength Fiber Reinforced Concrete Beams[J]. ACI Structural Journal,1993,90(3):279-287.
[2]SI L A,FERRIER E,JURKIEWIEZ B,et al. Static Behaviour of Steel-concrete Beam Connected by Bonding[J]. Engineering Structures,2007,29(6):1034-1042.
[3]李莉.活性粉末混凝土梁受力性能及设计方法研究[D].哈尔滨:哈尔滨工业大学,2010.
[4]丁振坤,邱洪兴,胡涛,等. HRB500级钢筋混凝土梁受弯刚度试验[J].建筑科学与工程学报,2009,26(1):115-120.
[5]覃维祖,曹峰.一种超高性能混凝土——活性粉末混凝土[J].工业建筑,1999,29(4):16-18.
[6]过镇海.钢筋混凝土原理[M].北京:清华大学出版社,2013.
[7]陈健,孙晓颖.钢纤维掺量对活性粉末混凝土初裂性能影响研究[J].混凝土,2007(3):46-48.
[8]中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局. GB 50010—2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2011.
[9]李美云,范参良. HRB400级钢筋混凝土构件变形的试验分析[J].工业建筑,2005,35(3):27-29.
[10]管巧艳.钢筋钢纤维高强混凝土梁受弯性能研究[D].郑州:郑州大学,2005.
[11]尚世仲.配高强钢筋混凝土梁的受弯性能试验研究[D].上海:同济大学,2007.
(责任审编赵其文)
Calculation Method of Deflection of RPC(Reactive Powder Concrete)Simply Supported Girder Reinforced by HRB 500 Rebars
FU Qiang,MA Hongwei,LUO Lina
(Guangxi Key Laboratory of Geomechanics and Geotechnical Engineering,Guilin University of Technology,Guilin Guangxi 541004,China)
AbstractT o investigate the deflection calculation method of RPC(Reactive Powder Concrete)girders reinforced by high strength rebars,4 simply supported girders with different reinforcement ratio were tested. T he results show that the measured deflection is smaller than the calculated value by 16%based on the calculation for ordinary reinforced concrete girder. Based on the test,a deflection reduction factor 0. 84 was introduced to the calculation equation for ordinary reinforced concrete girders and this new equation was suggested for the deflection calculation of RPC girders. In this way,the calculated deflection will be close to the test result.
Key wordsHigh strength rebar;Reactive powder concrete;RPC girder;Deflection calculation
中图分类号TU375. 1
文献标识码A
DOI:10. 3969 /j. issn. 1003-1995. 2016. 05. 20
文章编号:1003-1995(2016)05-0091-04
收稿日期:2015-11-07;修回日期:2016-02-16
基金项目:国家自然科学基金项目(51368013);广西重点实验室项目(2015-A-02)
作者简介:付强(1963—),女,副教授。
