乌干达Albert盆地J油田复杂碎屑岩储层含水饱和度定量表征*

徐 伟 杨小丽 房 磊 刘 钧 宋蓉燕

(中海油研究总院 北京 100028)

乌干达Albert盆地J油田复杂碎屑岩储层含水饱和度定量表征*

徐 伟 杨小丽 房 磊 刘 钧 宋蓉燕

(中海油研究总院 北京 100028)

在复杂碎屑岩储层中，测井解释的含水饱和度结果往往受井眼条件、测井质量等因素影响而存在较大偏差。为了更精确地表征含水饱和度的空间分布特征，以乌干达Albert盆地J油田为例，应用与储层物性和烃柱高度有关的SHF(Saturation Height Function)方法推导了该油田含水饱和度计算公式，即首先根据特殊岩心分析实验参数，将毛管压力转化到地层条件下，再对每个样品采用Lambda公式(Sw=ApcB+C)拟合，得到各条毛管压力曲线对应的系数A、B、C；然后通过对各系数与储层孔隙度和渗透率进行回归分析，获得各系数与对应物性的函数关系，从而得到含水饱和度计算公式，并通过对比计算结果与测井解释结果进行差异性检验。应用效果表明，本文公式得出的饱和度结果与测井解释结果具有极高的一致性，对于薄层砂岩能够提供更精确的结果，而且含水饱和度用数学公式表示后还能够更加方便地应用到三维地质模型和动态油藏模型中。

含水饱和度；SHF方法；碎屑岩储层；Albert盆地；乌干达

饱和度是油气藏储量计算的重要参数，定量表征饱和度的空间变化是编制油田开发方案的关键技术之一[1-2]。在复杂的碎屑岩储层中，测井解释的饱和度结果往往受到井眼条件和测井质量的影响而存在较大偏差，特别是对于薄层含油砂岩，由于电阻率受边界效应的强烈干扰，导致含油饱和度的解释异常偏低[3]。李秋实 等[4]对阿尔奇公式与储层物性之间的关系做了初步探讨，但是并未给出定量的关系。事实上，受岩性、物性及深度等因素的影响，测井解释饱和度结果难以直接通过井间对比扩展到三维空间。童凯军 等[5]利用毛管压力曲线推导渗透率估算模型，为利用毛管压力数据建立饱和度与储层物性之间的联系提供了借鉴。

为了定量表征含水饱和度的空间分布特征，本文以Albert盆地北部的J油田为例，利用岩心特殊分析实验得到的毛管压力数据，通过SHF(Saturation Height Function)方法的Lambda公式拟合和回归分析[6]，将含水饱和度与储层物性和烃柱高度联系起来，推导了该油田含水饱和度计算公式,并进行了应用效果分析。

1 地质背景

乌干达Albert盆地位于东非大裂谷西支北端，受基底构造控制，断层较为发育，是一个富含油气的中—新生代地堑(图1)，大部分被深湖所覆盖。Albert地堑变质岩基底以片麻岩、片岩、石英岩、花岗岩为主，之上为风化壳，上覆充填了从中新统至全新统的多套裂谷地层[7]。 J油田位于Albert盆地北部，原油油品较好，属轻中质原油，目前钻有6口井，其中J-2A井岩心资料较为齐全。该油田受边界断层控制，属带气顶的半背斜构造，主断层为北东—南西向，次级断层极为发育[8]。

本次研究的目的层段位于上上新统，埋藏较浅，压实作用弱,从上至下可细分为H30、H27U、H27L、H25、H17、H15等6个小层，其中H27、H25、H15层为主力储层。研究区属河湖过渡环境的碎屑岩沉积，主要发育湖相三角洲沉积，储层以分流水道砂体为主[9],平面上水道分支交叉并相互切割，垂向上相互叠置，储层空间分布十分复杂;储层物性好，为高孔高渗特征，层间、层内非均质性强[10]。

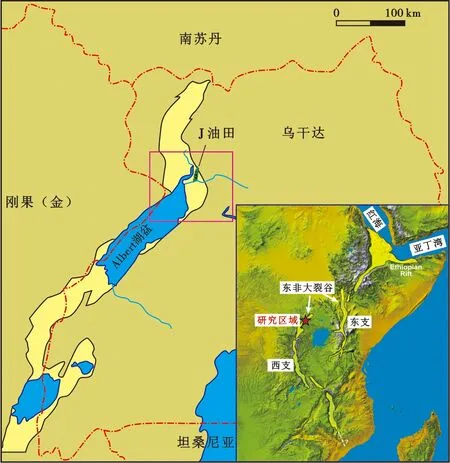
图1 乌干达Albert盆地构造与地理位置

2 含水饱和度公式推导

本次研究先采用SHF(Saturation Height Function)方法，选取乌干达Albert盆地J油田29条毛管压力曲线进行Lambda公式拟合，得到各样品对应的系数A、B、C；再通过对各系数与岩心孔隙度和渗透率进行回归分析，将各系数与储层物性参数联系起来，得到含水饱和度计算公式，并通过对比计算结果与测井解释结果进行差异性检验，确保计算公式的合理性；最后将本文公式应用到三维地质模型中去，精细刻画含水饱和度的空间分布特征。

2.1 毛管压力曲线Lambda公式拟合

在特殊岩心实验中，毛管压力曲线的测定实际上是模拟油气藏形成过程中油驱替水的过程，因此利用毛管压力资料来研究岩样的孔喉分布、含水饱和度等重要参数都与实际情况有很高的符合度[11-12]，特别是在油基泥浆取心等第一手资料较少的情况下，利用毛管压力数据求取含水饱和度尤其重要。

J油田J-2井进行了9次取心，主要取心层段位于H30—H15，共计47.1 m。在特殊岩心实验中，通过压汞法、半渗透隔板法和离心法测定了多个岩心样品的毛管压力曲线。首先根据实验参数将实验室条件下的毛管压力转换到储层条件[13]，转换公式为

(1)

式(1)中：pc为毛管压力，MPa；σ为表面张力，N/m；θ为接触角，(°)。

根据前人的研究，在所有的SHF(Saturation Height Function)拟合方法中，Lambda公式(式2)能给出最好的结果，因此选取该公式进行毛管压力拟合，拟合结果见表1。

Sw=ApcB+C

(2)

式(2)中：Sw为含水饱和度，f；A、B、C为公式系数。

2.2 系数与储层物性回归

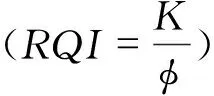
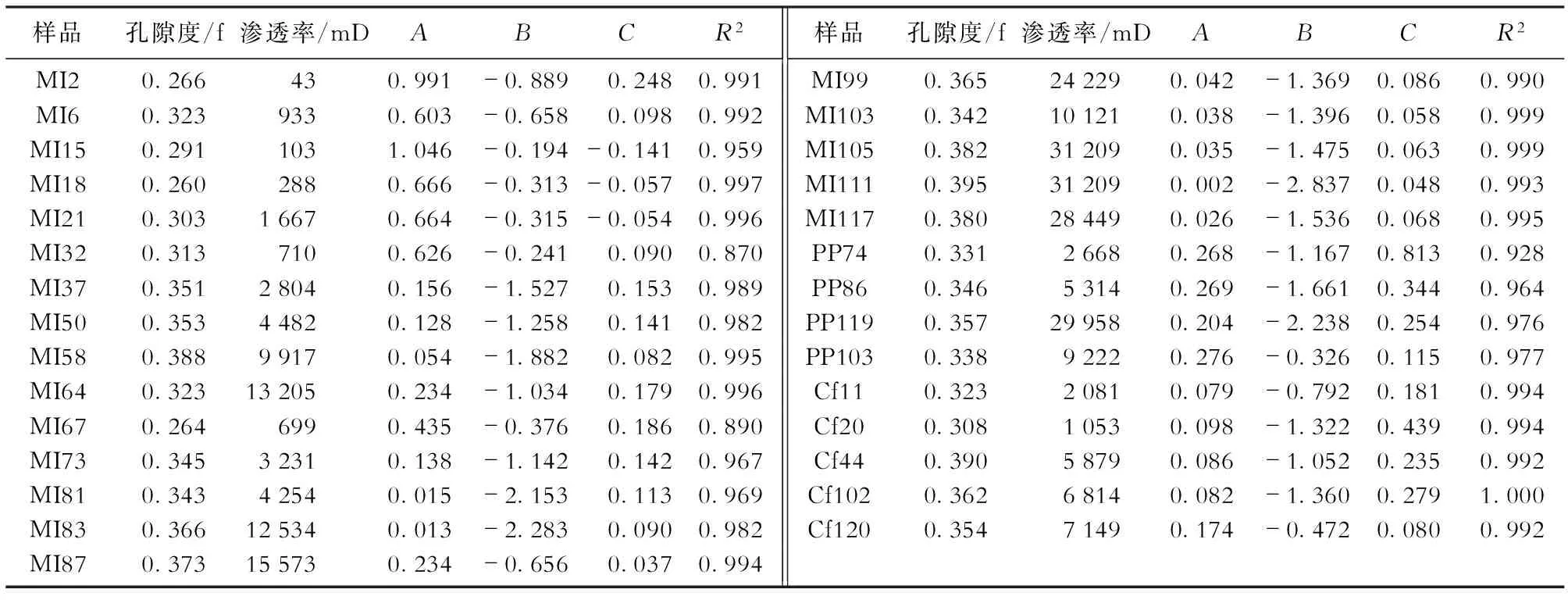
表1 J油田毛管压力曲线Lambda拟合结果

注：孔隙度、渗透率为岩心常规分析化验结果。

图2 J油田Lambda公式系数与储层品质指数对数(lnRQI)回归分析

图3 J油田Lambda公式系数与渗透率对数(lnK)回归分析

2.3 含水饱和度计算与差异性检验

利用油水界面以上烃柱高度(HaFWL)与毛管压力、流体密度差之间的关系，建立pc与HaFWL的函数关系式[14],即可求出油水界面以上各点处的毛管压力。

pc=HaFWL(ρw-ρo)/0.703 07=HaFWL/5.86

(3)

式(3)中：ρw为水密度，取值1.0 g/cm3；ρo为油密度，取值0.88 g/cm3。

结合式(2)、(3)及图2、3中的拟合公式，计算了J-2井油水界面之上的样品点(共8个)含水饱和度结果，并与测井解释结果进行了对比分析。结果表明，2组公式计算的饱和度结果与测井解释结果差值均集中于斜率为1的区域附近(图4)，总体上按照lnK回归公式计算的结果偏差为0.064， 而按照lnRQI回归公式计算的结果偏差为0.081。综合比较后，选择lnK回归公式作为最终计算公式。

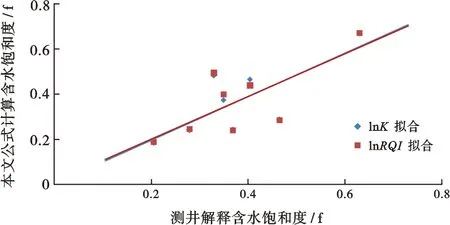
图4 本文公式计算含水饱和度与测井解释结果的差异性分析

3 应用效果分析

在三维地质模型中建立孔隙度和渗透率模型后，将本文推导出的J油田饱和度计算公式直接应用于三维地质模型中，精细地定量刻画了含油范围内储层含水饱和度在地下三维空间的分布特征。从连井剖面图(图5)上可以看出，测井解释结果(紫色曲线)与地质模型模拟结果一致，并且局部薄层砂岩中地质模型模拟结果更为精确。

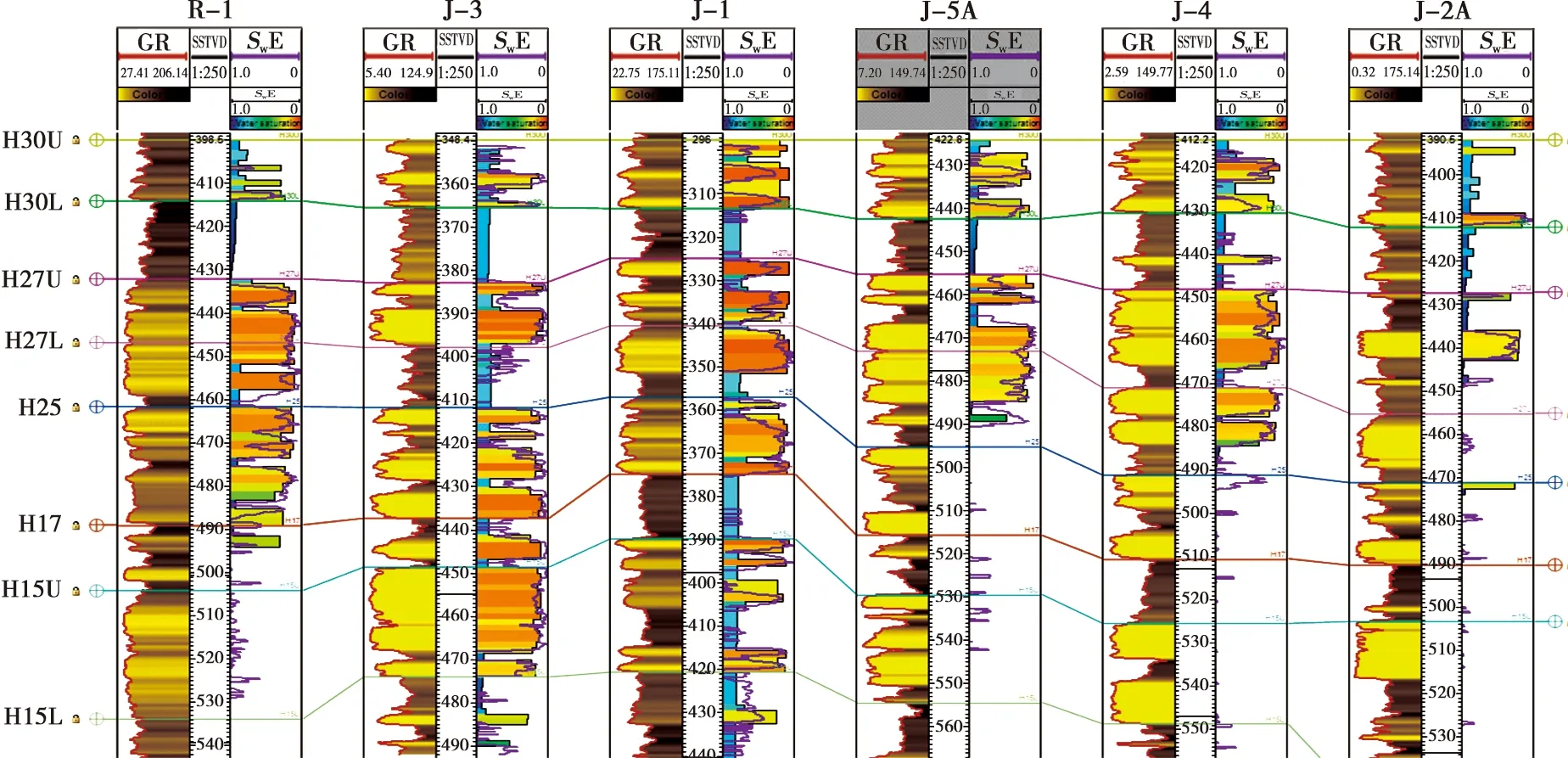
图5 J油田含水饱和度多井连井剖面图

J油田含水饱和度平面和剖面分布特征分别见图6，可以看出与通过随机插值得到的含水饱和度模型相比，本文方法计算结果更符合地质认识，含水饱和度在油水界面以内与储层物性相关，靠近油水界面附近逐渐升高；由于油品较好，地层产状较陡，几乎没有过渡带，到油水界面以外为纯水区。

从多井连井剖面(图5)可以看出，本文方法计算的含水饱和度在油柱高度大的位置明显低于油柱高度小的位置，符合地下实际油藏的特征。相应地，该油田油气水地下分布特征得以定量表征(图7)，为最终得到准确可控的石油地质储量奠定了坚实基础。

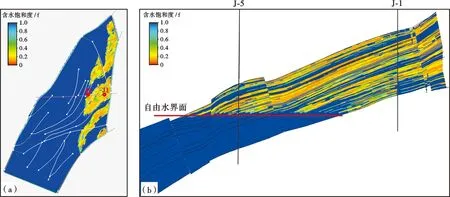
图6 J油田含水饱和度平面(a)和剖面(b)分布特征

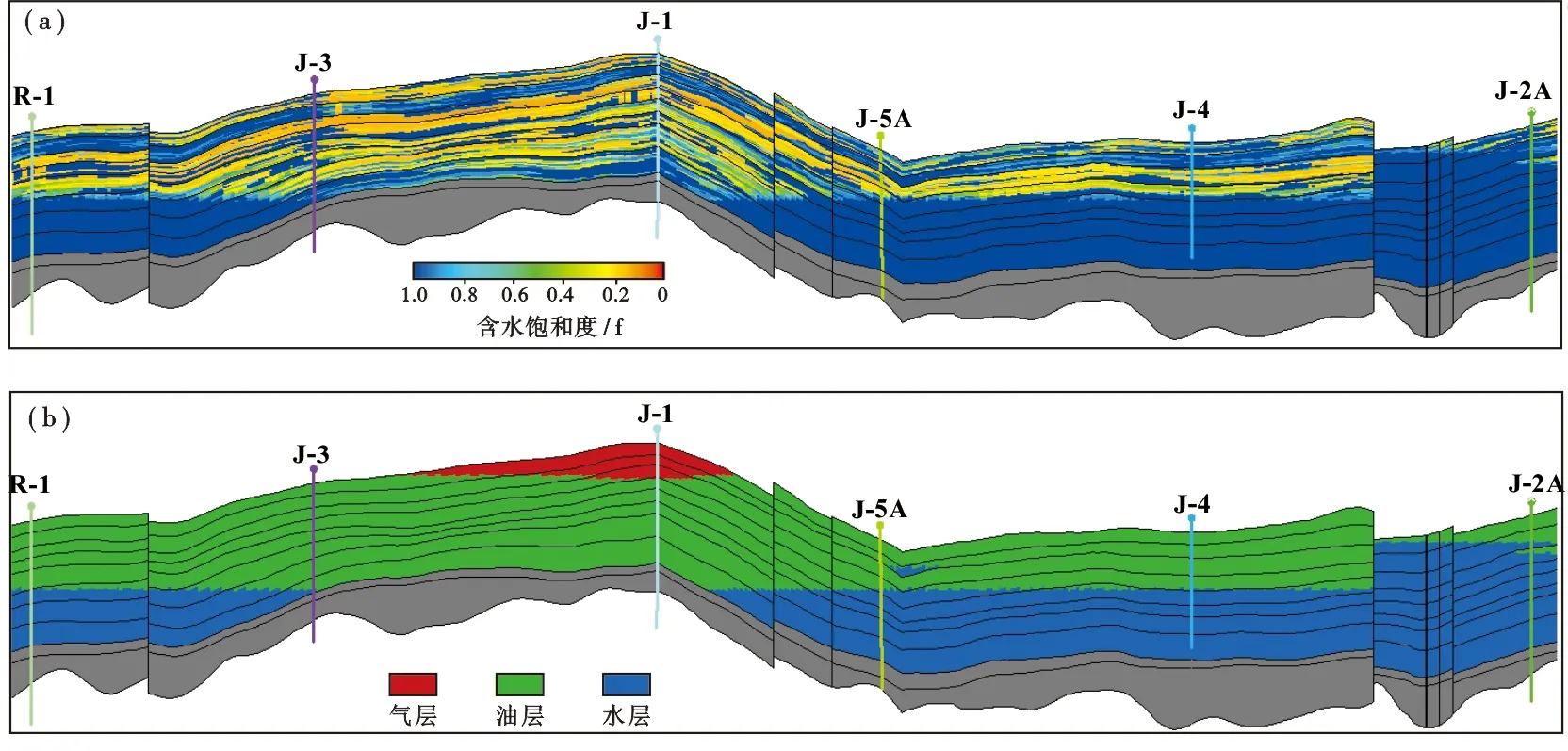
图7 J油田含水饱和度(a)和油气(b)分布特征

4 结论

根据岩心特殊实验毛管压力数据，采用SHF(Saturation Height Function)方法，推导了乌干达Albert盆地J油田的含水饱和度计算公式。利用该公式得出的饱和度结果与测井解释结果具有极高的一致性，并且能够更精确地评价薄层含油砂岩储层，消除了薄层砂岩饱和度因边界效应等产生的偏差,而且含水饱和度用数学公式表示后可以更加方便地应用到三维地质模型和粗化后的动态模型中去。需要注意的是，本文含水饱和度计算公式并不能完全替代测井解释方法，通常是在测井资料存在失真而导致解释结果不准或储层存在较多薄砂层时应用，而且其计算结果必须与测井解释结果进行对比分析，以确保计算结果的准确性。

[1] 鹿克峰，徐振中，冯景林．一种定量表征油水过渡区饱和度分布的实用方法[J]．中国海上油气，2011,23(6)：387-390,397．

Lu Kefeng,Xu Zhenzhong,Feng Jinglin.A practical method to quantitatively characterize oil saturation distribution in oil-water transition zones[J].China Offshore Oil and Gas,2011,23(6):387-390,397.

[2] 张玲，王志强，张丽艳，等．火成岩油气藏储量计算有关问题探讨[J]．石油与天然气地质，2009,30(2)：223-229．

Zhang Ling,Wang Zhiqiang,Zhang Liyan,et al.A discussion on certain issues concerning reserve calculation of igneous reservoirs[J].Oil & Gas Geology,2009,30(2):223-229.

[3] 廖明光，唐洪，苏崇华，等．W低阻油藏高不动水饱和度的成因及对低阻油层的影响[J]．石油实验地质，2010,32(4)：353-357,361．Liao Mingguang,Tang Hong,Su Chonghua,et al.Genesis of high immobile water saturation in the W low resistivity reservoirs and its influence on the low resistivity reservoir[J].Petroleum Geology and Experiment,2010,32(4):353-357,361.

[4] 李秋实，周荣安，张金功，等．阿尔奇公式与储层孔隙结构的关系[J]．石油与天然气地质，2002,23(4)：364-367．

Li Qiushi,Zhou Rongan,Zhang Jingong,et al.Relations between Archie's formula and reservoir pore structure[J].Oil & Gas Geology,2002,23(4):364-367.

[5] 童凯军，单钰铭，王道串，等．基于毛管压力曲线的储层渗透率估算模型:以塔里木盆地上泥盆统某砂岩组为例[J]．石油与天然气地质，2008,29(6)：812-818．

Tong Kaijun,Shan Yuming,Wang Daochuan,et al.CP-curve-based model for estimating reservoir permeability:an example from a sandstone of the Upper Devonian in Tarim Basin[J].Oil & Gas Geology,2008,29(6):812-818.

[6] 杨胜来．油层物理学[M]．北京：石油工业出版社，2004：230-231．

[7] DOU Lirong,WANG Jianjun,CHENG Dingsheng,et al.Geological conditions and petroleum exploration potential of the Albertine graben of Uganda[J].Acta Geologica Sinica,2004,78(4):1002-1010.

[8] 徐伟，杨小丽，李雪，等．乌干达Albert盆地北部上新统旋回地层学研究[J]．地质科技情报，2015,34(1)：57-62．Xu Wei,Yang Xiaoli,Li Xue,et al.Milankovitch cyclostratigraphy of Pliocene in the North Albert basin,Uganda[J].Geological Science and Technology Information,2015,34(1):57-62.

[9] 杨小丽，胡光义，庞玉茂，等．Albert湖盆北区退积型浅水三角洲沉积及储层特征[J]．中国海上油气，2015,27(5)：55-61,75．Yang Xiaoli,Hu Guangyi,Pang Yumao,et al.Retrogradation shallow water delta sedimentary model and reservoir characteristics in North area of Albert lacustrine basin[J].China Offshore Oil and Gas,2015,27(5):55-61,75.

[10] 于水，韩文明，赵伟，等．裂谷盆地陡断带三角洲沉积特征与成因模式：以东非裂谷Albertine地堑为例[J]．中国海上油气，2013,25(6)：31-35．

Yu Shui,Han Wenming,Zhao Wei,et al.Delta sedimentation and origin model within steep faulted zones in rift basins:a case of Albertine graben in East African Rift Valley[J].China Offshore Oil and Gas,2013,25(6):31-35.

[11] CHUDI O,SIMON R，OMOBUDE O.Saturation modeling in a geological complex clastic reservoir using log derived saturation height function:a case study of the E2 reservoir,Era Eko field in the Niger Delta[C].SPE 140635,2010.

[12] 赵国欣，朱家俊，关丽．用毛管压力资料求取原始含油饱和度的方法[J]．中国石油大学学报(自然科学版)，2008,32(4)：38-41．

Zhao Guoxin,Zhu Jiajun,Guan Li.Method of applying capillary pressure data to calculate initial oil saturation[J].Journal of China University of Petroleum(Edition of Natural Science),2008,32(4):38-41.

[13] KAMALYAR K,SHEIKHI Y,JAMIALAHMADI M.An investigation of using different saturation height function in an Iranian oil reservoir[J].Petroleum Science and Technology,2012,30(4):412-424.

[14] 宁方兴．济阳坳陷地层油气藏油柱高度主控因素及定量计算[J]．油气地质与采收率，2008,15(3)：9-11．

Ning Fangxing.Main controlling factors and quantitative calculation of oil column height of the stratigraphic hydrocarbon reservoirs in Jiyang Depression[J].Petroleum Geology and Recovery Efficiency,2008,15(3):9-11.

(编辑：杨 滨)

Quantitative characterization of water saturation in complex clastic reservoir of J oilfield, Albert basin, Uganda

Xu Wei Yang Xiaoli Fang Lei Liu Jun Song Rongyan

(CNOOCResearchInstitute,Beijing100028,China)

In complex clastic reservoirs, the water saturation derived from well logs is always influenced by borehole conditions and well logging quality and may generate great errors in the results. To characterize the spatial distribution of water saturation more accurately, taking the J oilfield in Uganda Albert basin for an example, the SHF method which relates reservoir petrophysical property and hydrocarbon height is applied to deduce the formula of water saturation calculation. Firstly, the capillary pressure is converted to reservoir condition according to special core analysis experiment parameters, and the Lambda fit(Sw=ApcB+C)to each sample is used to obtain a series of corresponding factorsA,BandC. Then, by making the regression between each factor and reservoir porosity and permeability, the coherent relation between each factor and reservoir petrophysical properties is obtained and the water saturation is calculated. Finally, the differences are examined by comparing the calculated results with the well logging interpretation results. The applied results show that water saturation derived from the proposed formula is highly consistent with well logging interpretation and the formula provides more accurate results in thinner sands. The water saturation mathematic formulas can be easily used in 3D geological model and dynamic reservoir model.

water saturation; SHF method; clastic reservoir; Albert basin; Uganda

徐伟，男，工程师，2011年毕业于中国地质大学(武汉)矿产普查与勘探专业，获硕士学位，主要从事海外油气田开发地质研究工作。地址：北京市朝阳区太阳宫南街6号院B座607(邮编：100028)。E-mail:xuwei6@cnooc.com.cn。

1673-1506(2016)02-0088-06

10.11935/j.issn.1673-1506.2016.02.011

TE 32+1

A

2015-02-01 改回日期：2015-04-29

*“十二五”国家科技重大专项“西非、亚太及南美典型油气田开发关键技术研究(编号：2011ZX05030-005)”部分研究成果。

徐伟,杨小丽,房磊，等.乌干达Albert盆地J油田复杂碎屑岩储层含水饱和度定量表征[J].中国海上油气，2016,28(2)：88-93.

Xu Wei,Yang Xiaoli,Fang Lei,et al.Quantitative characterization of water saturation in complex clastic reservoir of J oilfield, Albert basin,Uganda[J].China Offshore Oil and Gas,2016,28(2):88-93.