电动汽车电池建模及放电管理研究

程方晓,　李腾飞,　王　旭

(长春工业大学 电气与电子工程学院， 吉林 长春　130012)



电动汽车电池建模及放电管理研究

程方晓,李腾飞,王旭

(长春工业大学 电气与电子工程学院， 吉林 长春130012)

摘要：基于电池的额定容量效应和恢复效应的特性，采用脉冲放电策略建立电池组随机模型，马尔可夫决策过程理论和线性规划理论对电池组的放电能量均衡问题进行仿真控制。

关键词：电池模型； 脉冲放电； 马尔可夫决策； 线性规划

0引言

电池的额定容量效应和恢复效应影响电池实际释放的容量，对于采用由单体蓄电池串联的方式承担着车辆的全部功率负荷的纯电动汽车电池组而言,电池组达到放电电压极限值后停止放电静置一段时间，电池电量会有一定的恢复[1]。虽然单体电池的性能好，但若串联成一组使用，由于各个电池的特性不一致，会导致电池组性能急剧衰退或部分电池的加速损坏。在保证电池组正常功率负荷，使电池能量得到恢复，利用得到最大化的思想下，文中基于随机电池模型,采用马尔可夫决策过程理论和线性规划理论对电池组的能量均衡问题进行研究，解决续驶里程和电池寿命问题[2]。

1单体电池放电过程模拟分析

构建一个以电荷单元(q=i·t)为参考变量的电池模型，其用来描述电池的容量。也就是理论容量C；在进行恒流放电的情况下，电池不间断放电时，实际放出电量的大小为名义容量N。电池采用脉冲放电，其过程中会存在停止放电的间隙，在这短暂的时间内会恢复部分电量，这样，电池实际提供的容量Q介于理论容量C与名义容量N之间[3]。然后通过Q与N之间的关系设计不同放电策略。

文中采用可用离散时间的Markov过程对电池模型进行论述，电池中存在的电量可以用连续的数值代替，其中,Xn(n=0,1,2,…)代表离散的时间段0≤Xn≤N，如图1所示。

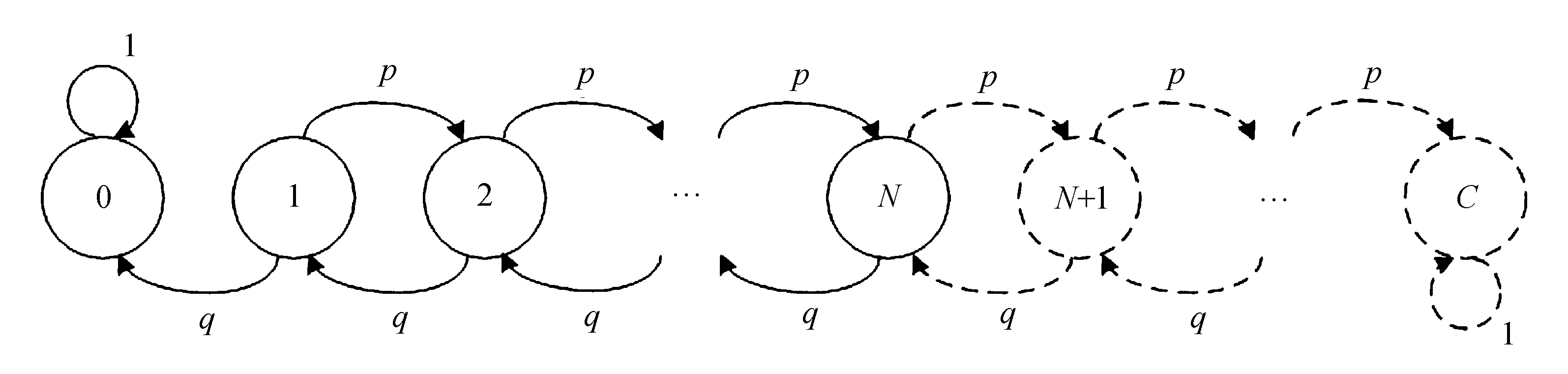
图1　单脉冲随机电池模型

比如当Xn=i时，其表示某时间段n可以使用的电池容量为i。为了使研究简单化，该电池模型是假设电池在状态0≤Xn≤N时进行放电，此过程放掉一个电荷单元的电量的概率为固定常数q，恢复一个电荷单元的电量的概率为固定常数p，q和p为状态转移概率。由此可以将其转变为齐次Markov过程，根据状态转移概率的性质可以得出结论：p+q=1。当Xn=0时，电池的电性能便受到极大影响，其放电能力被大大削弱，将以100%的概率始终处于0电量状态，因此Xn=0处于恢复电量的状态。

2放电过程的模拟

2.1放电概率的确定

在实现仿真模拟时，需要通过一定的方式实现控制概率q放电，控制概率p以实现电荷的回归。如果通过任意变量X代表一种放电或充电电荷的状态，那么在X=0的时候意味着电荷处于充满状态，在X=1的时候代表电荷处于放电状态。那么现在面临的问题就变成了通过何种方法实现在任意变量X等于0时，概率等于p，在任意变量X等于1时，概率等于q。在仿真的实验环境下,可以通过平均分布任意数产生装置rand来完成参数的选取，平均分布任意数产生装置可以确定在区间范围内的平均分布随机参数，定义为u。在使用平均分布任意数产生装置rand后，如果选取的随机量u≤q，那么就可以认定电池处于放电状态,即X=1，此时电池减少了一个单元的电量；如果选取的随机量u>q，那么可以认定电池处于充电状态,即X=0，此时电池增加一个单元的电量。我们对电量增减的科学性做如下说明：

因为在[0,1]的区间范围内随机参数产生器rand确定的任意参数为u，因此任意参数u的概率范围内的密度概率等于1，可以得到：

(1)

(2)

式(1)、式(2)代表假如产生器rand产生的随机参数u≤q,那么就可以认定开关是关闭的;假如产生器rand产生的随机参数u>q,那么就可以认定开关是打开的。

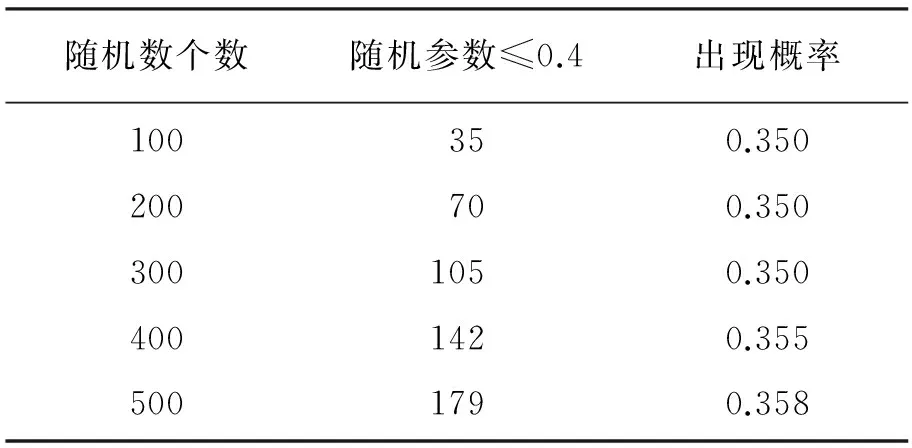
表1　随机参数≤0.4的概率分布

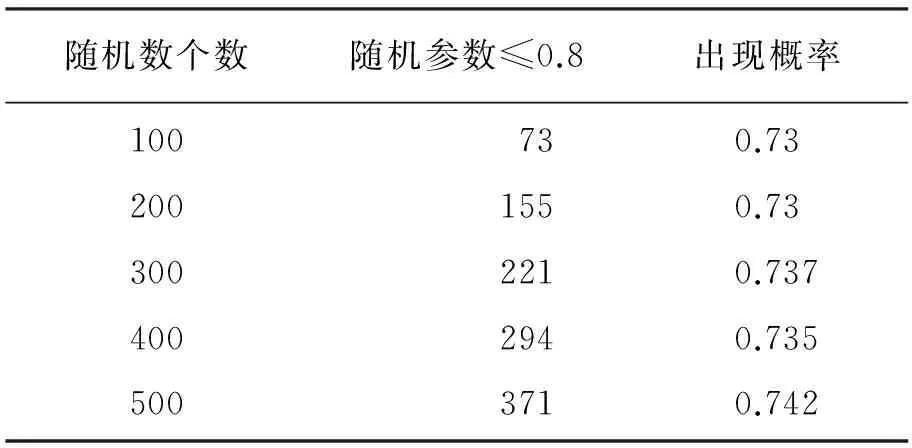
表2　随机参数≤0.8的概率分布

在MATLAB仿真模拟系统下，表1和表2中的实验数据是通过任意参数产生器rand分别选用150、250、350、450和550个任意参数时，通过以0.1为初始值及公差为0.1时选取的随机数进行统计分析。从图中可以看出，由于rand生成随机数的概率分布与应用要求相差不大，故任意选取对小于或等于0.4和0.8的随机数进行统计得到的随机数概率分布情况,可用于表示电池放电概率和充电电量概率。

2.2电量的仿真

电池在名义容量N取值为100、理论容量C取值为140的理想状态下，在各种不同的放电概率情况下电池可以使用的容量随着时间变化的仿真数据如图2所示。

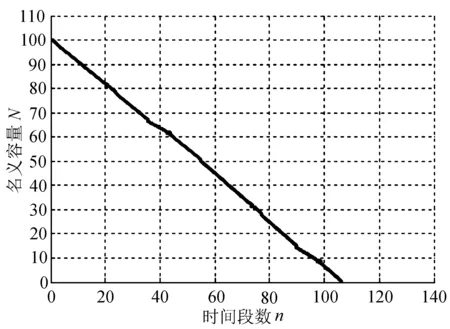
(a) 放电概率0.8

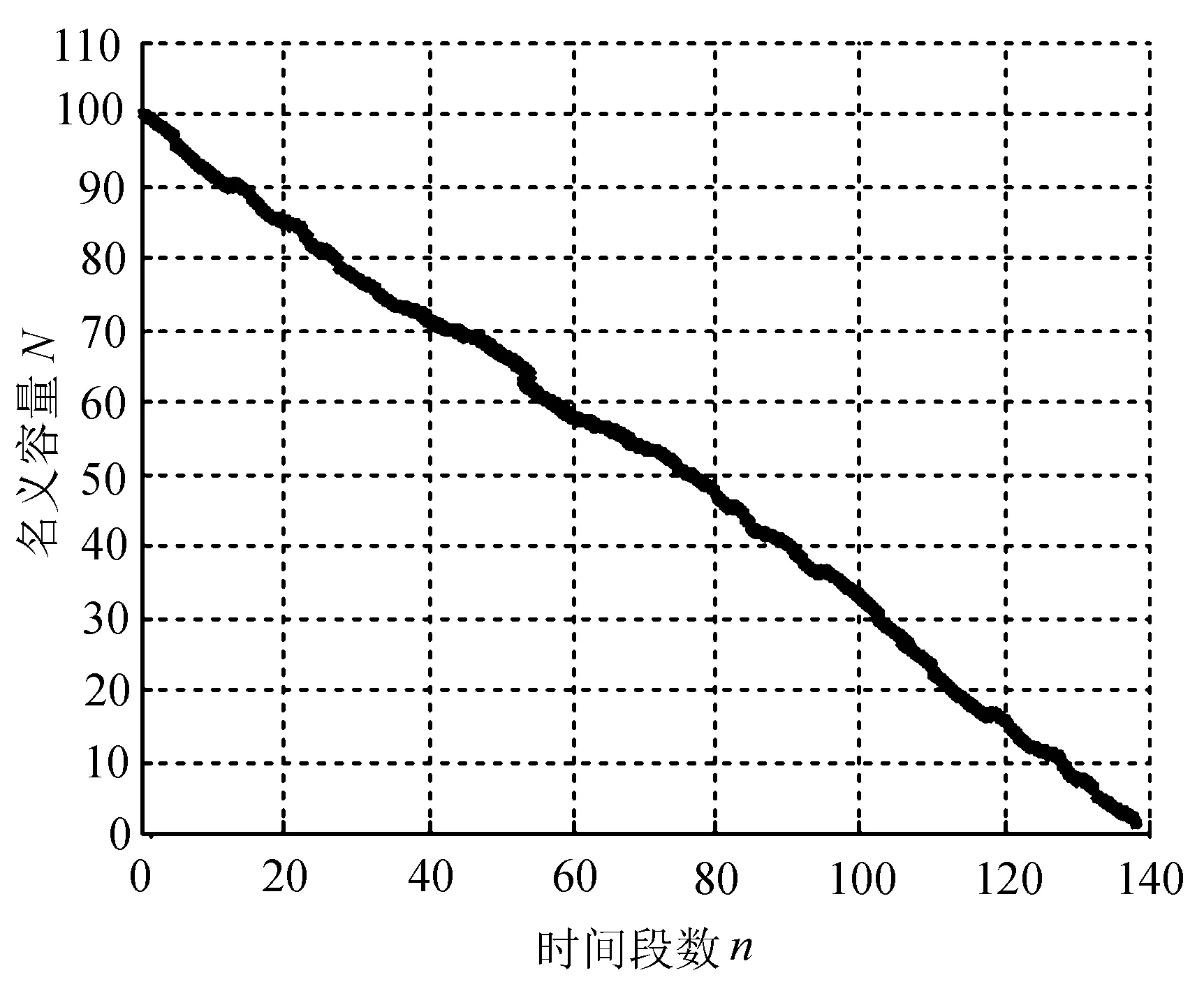
(b) 放电概率0.6

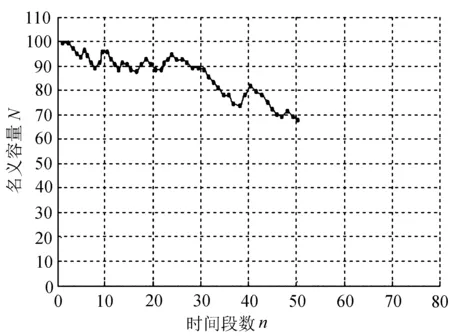
(c) 放电概率0.4

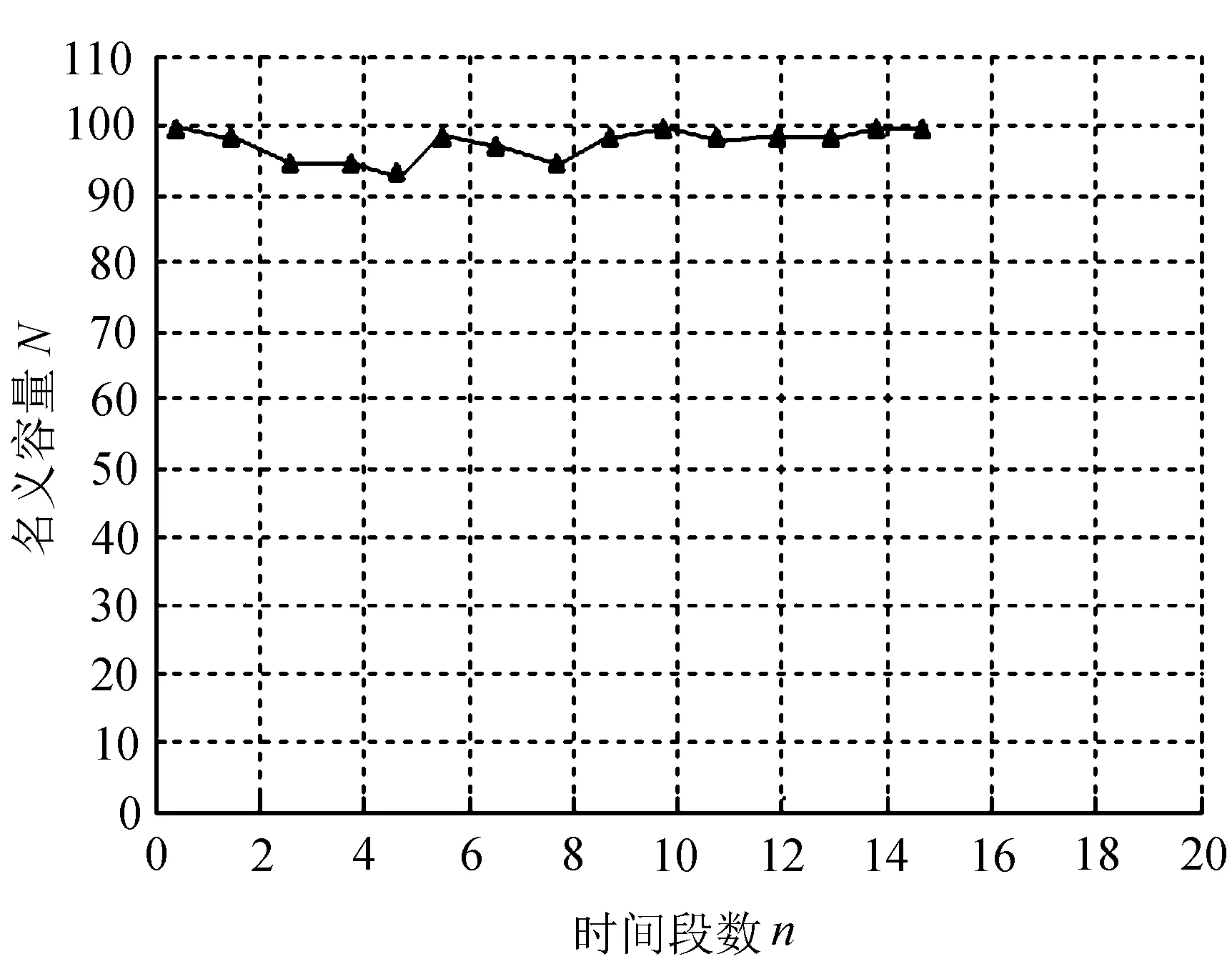
(d) 放电概率0.2

因为每次试验的情况不一致，这就导致了每次仿真的数据不会完全一致，可是仿真数据曲线的趋势是一样的。经过分析可知,图2(a)中的放电电荷概率等于0.8，那么这次的仿真数据结果从开始到状态变为吸收态时N=0结束，电池放电次数总计达到106次，达到充电满电回归状态有6次，最后留下的电量单元达到45个。图2(b)中的放电电荷概率等于0.6，那么这次的仿真数据结果从开始到状态变为吸收态时N=0结束，电池放电次数总计达到127次，达到充电满电回归状态有27次，最后留下的电量单元达到15个。图2(c)中的放电电荷概率等于0.4，那么这次的仿真电池放电次数总计达到52次，达到充电满电回归状态有41次。图2(d)中的放电电荷概率等于0.2，那么这次的仿真电池放电次数总计达到16次，达到充电满电回归状态有40次。从图2中可以得到如下结论，即电荷放电的概率越大，那么相应的仿真曲线下降的趋势越大。而且在电池放电概率不断降低的过程中，电荷仿真模拟曲线的趋势是从开始的直线变为曲折线，最后再走到平直的一个变化过程。从上面的实验数据足可以证明：电池电荷的回归统计数会随着电池电量放电概率的升高而降低，仿真模拟的电池残余的电量单元反而会随着电池放电概率的升高而升高。

为了验证之前仿真实验数据的科学性，通过变化参数N和C，对变化参数后的系统再次进行了多次仿真。电池在名义容量N取值为400、理论容量C取值为500的理想状态下，在各种不同的放电概率情况下,电池可以使用的容量随着时间变化的仿真数据如图3所示。

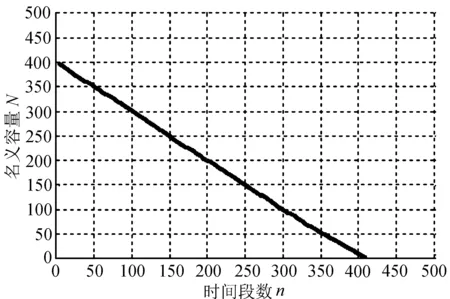
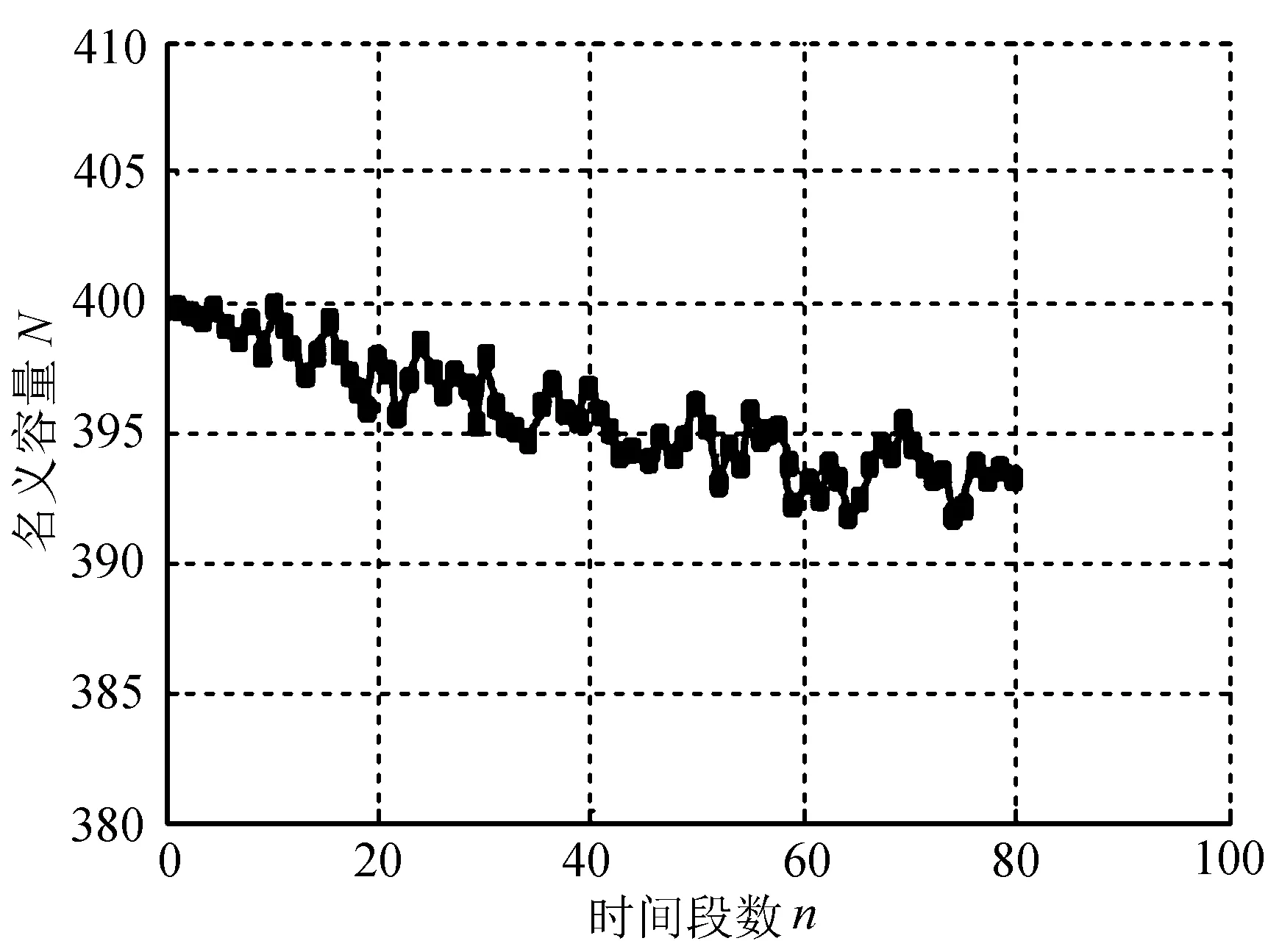
通过图2与图3中的(a)、(b)、(c)、(d)比较可以看出：电荷放电概率的不断升高，各个对应的参数仿真曲线走向趋势仍然是一致的。图2(b)结束仿真模拟的原因是由于电荷已经处于吸收状态而引起的，图3(b)结束仿真模拟的原因是由于电池电荷统计的回归电荷数据已经升到了最高值而引起的仿真结束。由此可以得出结论，在某种程度上印证了电池电荷脉冲放电时电池回归满电能力越强，那么一定程度的放电概率能够提高电池的满电回归能力。

3电池放电过程研究

3.1电池模型建立

根据单体电池模型的相关性质，文中设计了相关电池模型,即在原有的电池串联基础上，对每个单体电池上并联一个单体电池。两个电池间用双向控制开关连接，工作时，每对电池任选一块与其他两对中的任意一块组合工作。并且双向控制开关由开关控制器进行控制导通或断开。具体模型如图4所示。

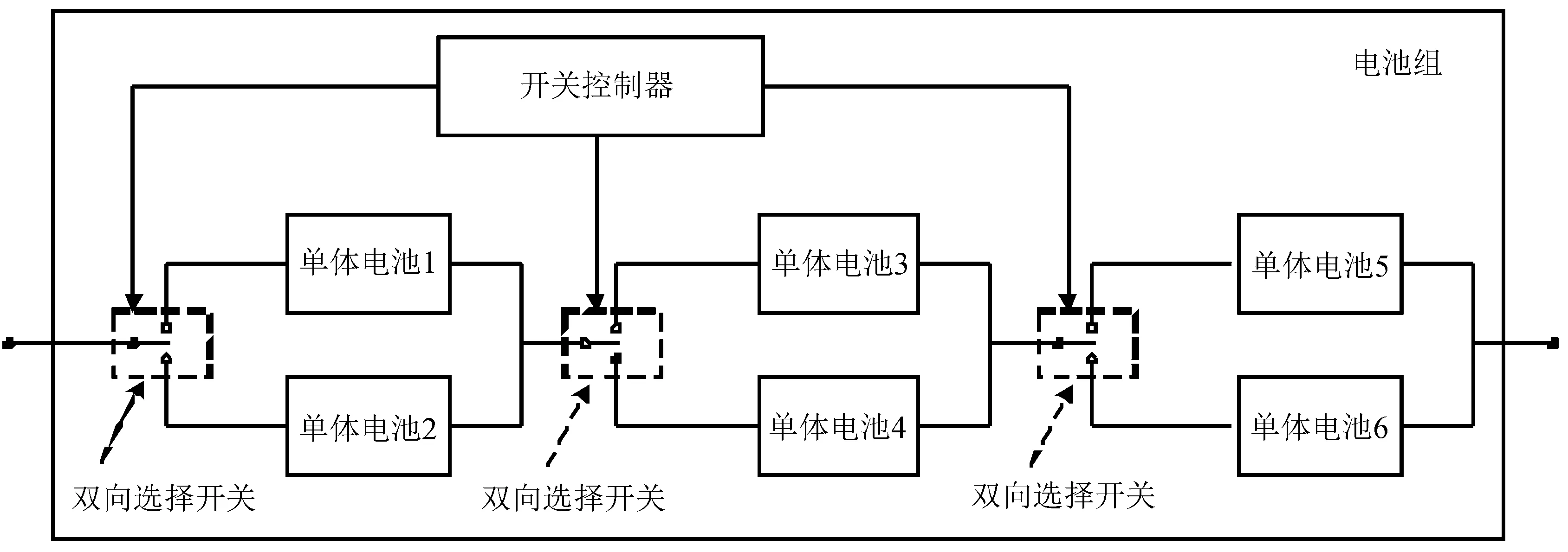
图4　电池模型

3.2基于马尔可夫决策过程求解模型

3.2.1马尔可夫决策过程简介

马尔可夫决策过程(MDP)是研究一类随机序贯决策问题的理论。离散时间马尔可夫决策过程模型[4]由如下的五重组组成：

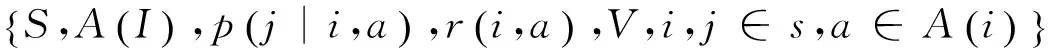
(3)

其中各项的含义为：S是系统所有可能的状态所组成的非空的状态集，有时也称之为系统的状态空间，它可以是有限的、可列的集或任意非空集。A(i)是在状态时可用的决策集，通常由多个决策a组成。p(j|i,a)是在某个决策时刻上采用决策a后，模型由状态i转移到状态j的概率。r(i,a)是模型在状态i采用决策a后所获得的报酬。S为准则函数(也称为目标函数)，是获得最佳策略的依据。

由以上定义可以看出，MDP的历史由相继的状态和决策组成，其形式为

(4)

决策便是通过某个最优值函数阶段性地确定这样一个历史。文中讨论应用马尔可夫决策过程建立最优电池调度策略问题，使得在续的T+l个决策时刻单个电池恢复的电荷量最多且实现能量均衡。这可以看作是求解电池组为T的电池最优调度问题。

3.2.2求解模型的建立

定义系统状态为Dt[N1t,N2t,N3t，…,Nnt]，N1t,N2t,N3t,…,Nnt为单体电池R1,R2,…,Rn于决策时刻t属于{0，1,2,…，T}时电池的当前名义容量。状态转移概率由控制器决策时间的情况决定:

(5)

式中：P(Dt+1|Dt,ati)----在决策时刻t时选择单体电池i后系统状态由Dt转移到Dt+1的概率。

任一决策时刻，控制器工作的概率表示为Pst，对于连续工作情况Pst=1。如果某单体电池导通，则它失去一个电荷单元，未导通电池,则以某个概率Pr恢复一个电荷单元。对于图5电池组模型，以其六块单体电池中的一组为例，当其中一个单体电池导通时，另一个单体电池要么以概率P(C-N)恢复一个电荷单元，要么以概率1-P(C-N)保持原状态不变。因此，在下一决策时刻会诱导出2个状态，见表3。

表3　状态转移概率与报酬

采用Bellman最优化原理对模型进行求解，使用以此向后迭代算法来选定各个关键时刻所要进行的活动，目的就是要把电池电荷回归满电量达到最高值。一般而言，最优策略的子策略同样是最优，这就是最优化原理[6]。所以，如果从最后时刻依次向前递推直至时刻0，以便选定在各个关键阶段时的最佳决定路线，从而进一步选择出最佳策略。由此可以得到递推公式如下:

(6)

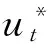
(7)

如果直接采用Markov决策对能量进行均衡管理，其过程较复杂且有很大的运算量，为了进一步减少运算量，文中通过线性规划的思想来简化模型的求解：将系统的状态由多维Dt(N1t,N2t,…,Nnt)转为1维Dt=(N1t+N2t+…+Nnt)后采用线性规划的方式求解:

(8)

下面针对电池内部一对并列单体电池状态来说明本方法如何实现。假如开始时有两个单体电池分别是电池1和电池2，电池理论上容量为C=200，名义上容量为N=150，即两个单体电池的电池能量是均衡的。过了一段时间，单元电池1的残余名义容量N1t取值为30，电荷电量回归概率等于0.5；单元电池2的残余名义容量N2t取值为21，电荷电量回归概率等于0.3；平衡状态为N1t=N2t=16。从表3得知，单体电池1在放电时单体电池2的电量回归数学期望值等于0.3，单体电池2在放电时单体电池1的电量回归数学期望值等于0.5。这样就把这个问题转化成了线性规划的资源分配问题。即把一种资源分配给两个用户，对于每一个单元的资源，用户1的收益占0.4，用户2的收益占0.2，如何合理分配资源才能使用户收益最大?

设划分给电池1的电量定义为x1，划分给电池2的电量定义为x2，有:

(9)

由于平衡态N1t=N2t=8，所以约束条件为:

(10)

初态N1t=30，N2t=20至平衡态N1t=N2t=16这一阶段，由图解法得x1=14,x2=4，即使电池1恢复14次，电池2恢复4次,可使电荷的恢复量最大。

4结语

通过电池组模型的建立，电池组整体电量经马尔可夫决策过程理论和线性规划理论分析，电池在放电过程中能量恢复可达12.8%，达到了比较好的效果。同时减缓了因串联导致的性能衰退现象。对于纯电动汽车而言，该模型可提高其续驶能力和延长电池寿命,具有重要价值。

参考文献：

[1]ThomasFFuller,MareDoyle,JohnNewman.Relaxationphenomenainlithium-ioninsertioncells[J].JournaloftheElectrochemicalSociety,1994,141(4):982-990.

[2]国家电动汽车试验示范区管理中心.浅谈“电动汽车中的电池能量管理系统” [C]//中国电动汽车会议论文集.2005:169-173.

[3]M Doyle, J Newman. Analysis of capacity-rate data for lithium batteries using simplified models of the discharge process[J]. Journal of Applied Electrochemistry,1997,27(7):846-856.

[4]Debashis Panigrahi, Carla chiasserini, Sujit Dey, et al. Battery life estimation for mobile embedded systems [C]//Fourth International Conference on VLSI Design.Bangalore India: [s.n.],2001:55-63.

[5]刘克.实用马尔可夫决策过程[M].北京：清华大学出版社,2004.

[6]刘开绪，付保红，邹立君.锂离子电池组能量均衡控制[J].长春工业大学学报：自然科学版，2010,31(5):407-411.

[7]王晓陵，陆军.最优化方法与最优控制[M].哈尔滨：哈尔滨工程大学出版社,2008.

[8]朱元，吴志红，田光宇，等.基于马尔可夫决策理论的燃料电池混合动力汽车能量管理策略[J].汽车工程，2006(9):798-802,828.

Electric vehicle battery modeling and discharge management

CHENG Fangxiao,LI Tengfei,WANG Xu

(School of Electrical & Electronic Engineering, Changchun University of Technology, Changchun 130012， China)

Abstract：With the effect of the battery rated capacity and recovery characteristics, pulse discharge technique is used to build a battery stochastic model. Both the Markov decision process theory and linear programming theory are applied to simulate the battery discharge energy equilibrium phenomena.

Key words：battery model; pulse discharge; Markov decision; linear programming.

收稿日期：2016-02-25

基金项目：吉林省科技发展计划基金资助项目(20120362)

作者简介：程方晓(1969-)，女，汉族，吉林长春人，长春工业大学副教授，博士,主要从事测控技术与智能系统方向研究,E-mail:chengfangxiao@ccut.edu.cn.

DOI:10.15923/j.cnki.cn22-1382/t.2016.2.11

中图分类号：TM 912

文献标志码：A

文章编号：1674-1374(2016)02-0159-06