基于第四方物流平台的快递末端网点优化整合∗

刘聪娜，周骞，何风

（1.长沙理工大学交通运输工程学院，湖南长沙 410004；2.长沙理工大学汽车与机械工程学院，湖南长沙 410004）



基于第四方物流平台的快递末端网点优化整合∗

刘聪娜1，周骞1，何风2

（1.长沙理工大学交通运输工程学院，湖南长沙 410004；2.长沙理工大学汽车与机械工程学院，湖南长沙 410004）

摘要：伴随着电子商务的高速发展，中国快递行业的发展势头十足，但长期以来，快递末端配送存在着服务水平低、管理混乱、资源浪费、专业化程度低等问题。文中借力第四方物流，运用第四方物流平台并通过建立共同配送中心整合快递末端配送资源，建立了末端网点优化整合模型；以3家快递企业为研究对象进行优化整合，结果表明该模型能起到很好的优化整合效果。

关键词：物流；第四方物流平台；共同配送；优化整合；快递末端网点；免疫遗传算法

随着电子商务的蓬勃发展，中国快递业进入高速发展阶段，据统计，快递业的业务量从2005年的8.658亿件迅速发展到2014年的136.9亿件，收入也由2005年的239.7亿元一跃发展到2014年的2 045.4亿元，发展速度惊人。但快递企业服务没能跟上，客户忠诚度不高，多家快递企业末端存在重复设置网点、车辆满载率不高、管理难度大、丢件和损件问题多、竞争力不足等问题，急需优化整合末端网点以提高服务水平，实现规模化，提高效率。

国内外针对快递行业存在的问题纷纷提出解决方案：张昕对比分析了整合快递配送的几种方法，指出这些方法都无法有效解决问题，而采用第三方物流平台整合快递末端配送实现规模经济可保证专业化服务，清晰成本分摊和收益分享；成玫颖提出了快递配送末端整合模式，重点研究了快递末端整合的收益分配问题，通过对比分析stackelberg博弈求解分散决策时固定付费、收入共享、服务水平补偿、收益共享与成本共担等4种收益分配方案，寻找系统最满意的分配方案；季宬等以大学城为研究对象，通过建立共同配送中心，进行实际数据的密度、成本和选址分析，并对南京大学建立末端共同配送中心提出了参考性建议；张永昕重点研究了兼并重组整合方式下基础物流网络优化问题，设计了快递基础设施网络优化整合模型，采用遗传算法进行模型求解；Kofi Q.Dadzie等认为企业通过整合双方的物流和渠道管理表现出强大的市场竞争力和更高的财务业绩，在企业竞争中应持续加强对供应链资源的整合力度；张露方等分析了电子商务末端配送中的症结，提出了将共同配送方式的理念应用到电子商务末端的策略；钟耀广描述了东莞电子商务城市末端配送的现状，总结了末端配送面临的问题并给出了末端配送优化策略。以上研究部分是针对快递末端优化整合的收益分析，部分则是定性给出了优化整合策略。该文基于第四方物流平台对快递末端网点进行优化整合，建立末端网点优化整合模型。

1　快递末端网点优化整合问题描述

基于第四方物流平台的快递末端网点优化整合，就是快递企业与第四方物流合作，借助第四方物流平台实现快递末端配送资源整合。一般而言，第四方物流有协同运作模式、方案集成商模式和行业创新者模型3种运作模式。第四方物流平台就是整合和管理所有信息、资源和技术以提供一致性的服务，达到资源整合、提高快递服务水平、减少成本的目的。第四方物流平台的业务流程可概括为会员注册流程、信息发布、订单提交和处理、合同签订和合同执行、金融结算。在利用第四方物流平台的基础上，在快递分拨中心和末端网点间建立共同配送中心，为多家快递企业共同配货至末端网点，同时将各末端网点从各客户聚集点的集货共同运输至配送中心，提高末端配送效率，减少成本（如图1所示）。

目前，中国快递企业数量众多，规模参差不齐。这里选取某区域甲、乙、丙3家快递企业为研究对象，对其现有末端网点进行重新优化整合，即从3家公司现有末端网点中选择恰当的网点予以保留并确定网点数目和位置。保留的末端网点需考虑其运营成本，不仅需用数目最少的网点满足顾客聚集点的需求，还要保证运营费用和配送中心到网点的运输费用及顾客聚集点到达这些末端网点的运输费用的总和最小。

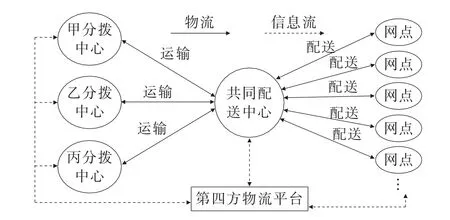
图1　基于第四方物流平台的共同配送示意图

2　数学模型构建

2.1末端网点优化整合问题假设

（1）由于建设有共同配送中心对3家企业的快件进行共同配送，对3家快递公司现有末端网点进行优化整合时，可以把3家公司在某一范围的全部末端网点看作一个整体进行优化，不因所属公司不同而区别对待。3家快递公司的末端网点分布如图2所示。

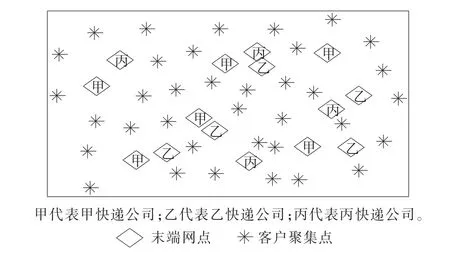
图2　3家快递公司末端网点分布示意图

（2）保留一个末端网点需要一定的运营费用，尽量用最少的网点去覆盖所有需求点。

（3）假定所有末端网点有最大的服务半径，超过这个范围，顾客聚集点就不在该末端网点的服务范围内。

（4）顾客群聚集点到末端网点的运输单价用两点的距离表示。

（5）当顾客聚集点在多个末端网点的服务半径内时，可将这些客户集中点的业务分配到多个末端网点处理。业务的分配需综合考虑末端网点到顾客聚集点间的距离和末端网点自身的服务能力。

2.2模型建立

选取某区域3家快递企业为研究对象，并简化快递企业的运作流程，在满足顾客需求及系统成本最小的目标下优化快递末端网点，确定所要保留末端网点的数目和位置。

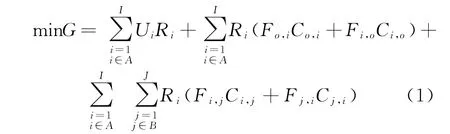
约束条件如下：

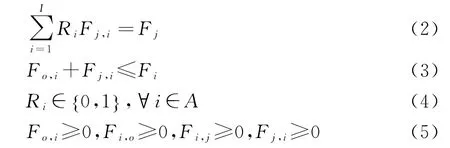
式（1）保证保留的末端网点运营固定成本、配送中心到网点的运输费用与各网点到客户群聚集点的运输成本之和最小；式（2）表示客户聚集点j的业务量被分配到各个末端网点的业务量之和等于该客户聚集点j的总业务量；式（3）表示从配送中心发往网点i的货物量与从顾客群聚集点j发往网点i的货物量之和小于网点i的最大容量；式（4）表示该变量是二进制变量；式（5）表示这些变量为非负变量。

3　模型求解

免疫遗传算法是一种基于生物进化免疫机制的改进的遗传算法，以待求解模型的目标函数来表示免疫遗传算法中的抗原，免疫系统生成的抗体即可表示为对应模型的解，抗原与抗体间的亲和力值表示可行解与最优解的接近程度。

假设免疫系统由N个抗体组成，采用二进制即0～1编码的方法，每个抗体基因长度为M，抗体基因如图3所示。

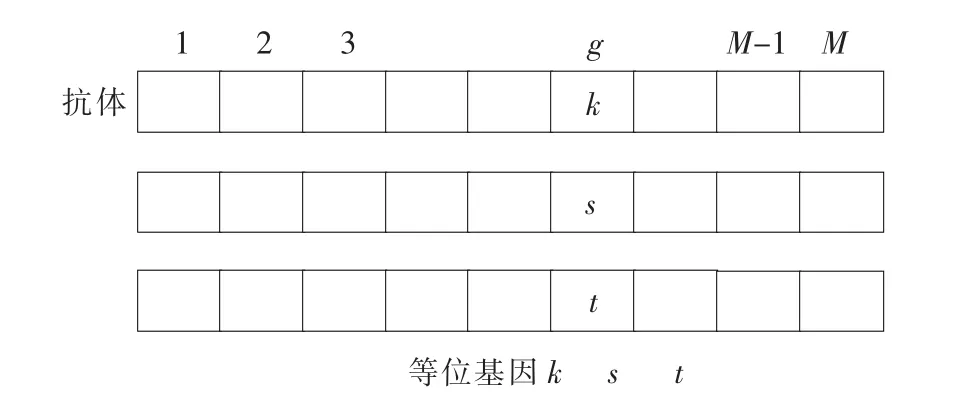
图3　抗体基因示意图

算法实现步骤（如图4所示）如下：

（1）抗原输入。输入快递末端网点优化整合模型的目标函数及相应约束条件。

（2）初始抗体的生成。当免疫系统首次遇到抗原并作出相应免疫应答后，初始群体随机生成。在免疫系统第二次遇到抗原并作出应答时，免疫机制开启记忆功能，使部分初始抗体能从记忆细胞中获得记忆功能，由于抗体在记忆细胞中有更高的适应度值，从而有效加快算法的收敛速度。

（3）计算抗体适应度函数及亲和度。适应度函数用来表示群体中各抗体在优化中与最优解的接近程度，其值越大则越接近最优解。因该模型目标函数是求解成本的最小值，故需将目标函数与适应度函数进行变换，变换方式见式（6）。抗原和抗体间的亲和度越高，则抗体质量越好且与最优解越接近。这里的亲和度为适应度函数的值。

式中：f（x）为适应度函数；Gf（x）为目标函数。

（4）记忆细胞更新。通过筛选出与抗原亲和度最高的抗体并用该抗体取代记忆细胞中的原有抗体，完成记忆细胞更新。

（5）抗体生成的促进和抑制。在搜寻最优解过程中，若种群中抗体浓度过大，会造成求解过程过于缓慢，导致算法过早收敛。因此，需限制抗体浓度。按式（7）计算抗体浓度De，并从中找出浓度较大的个体，记为个体1，2，…，t。t个个体的浓度概率pd按式（8）计算，其他N-t个个体的浓度概率pd按式（9）计算。运用改进轮盘赌选择法计算t个个体的适应度概率pf，适应度概率pf和浓度概率pd通过加权计算即得到个体的选择概率p［见式（10）］。个体适应度值越大则其被选择的概率越大，个体浓度越大则其被选择概率越小。

式中：λ为相似度常数，0.9≤λ≤1。

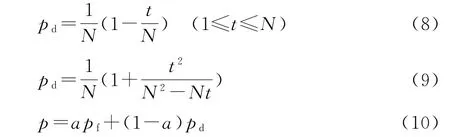
式中：a为亲和系数，a＞0；pf＜1；pd＜1。

（6）群体更新。免疫遗传算法与遗传算法中的交叉操作和变异操作方法相同，即随机挑出2个抗体按设定的变异概率进行变异，再进行交叉。重复执行步骤3～6，直到符合算法的终止条件。

（7）终止条件判断。当所设定的参数满足算法终止条件时，算法结束并输出最优解；否则，转向步骤3。

图4　免疫遗传算法流程

4　构造算例

某区域有甲、乙、丙3家快递企业与第四方物流进行合作，建立共同配送中心提供配送服务并分别对末端网点统一配送，配送中心坐标为（2 800，2 500）m，下面运用上述模型对末端网点进行优化整合，减少成本。3家快递企业现有末端网点信息如表1所示，顾客聚集群信息如表2所示，现有末端网点及顾客聚集点的分布位置如图5所示。

将初始群体规模取为50，采用二进制即0～1编码方法对待整合的末端网点进行编码设计，其中“0”表示该站点未被选中，“1”表示该站点被选中，最后结果全部为1的即为要保留的末端网点。免疫遗传算法的优化参数如表3所示。

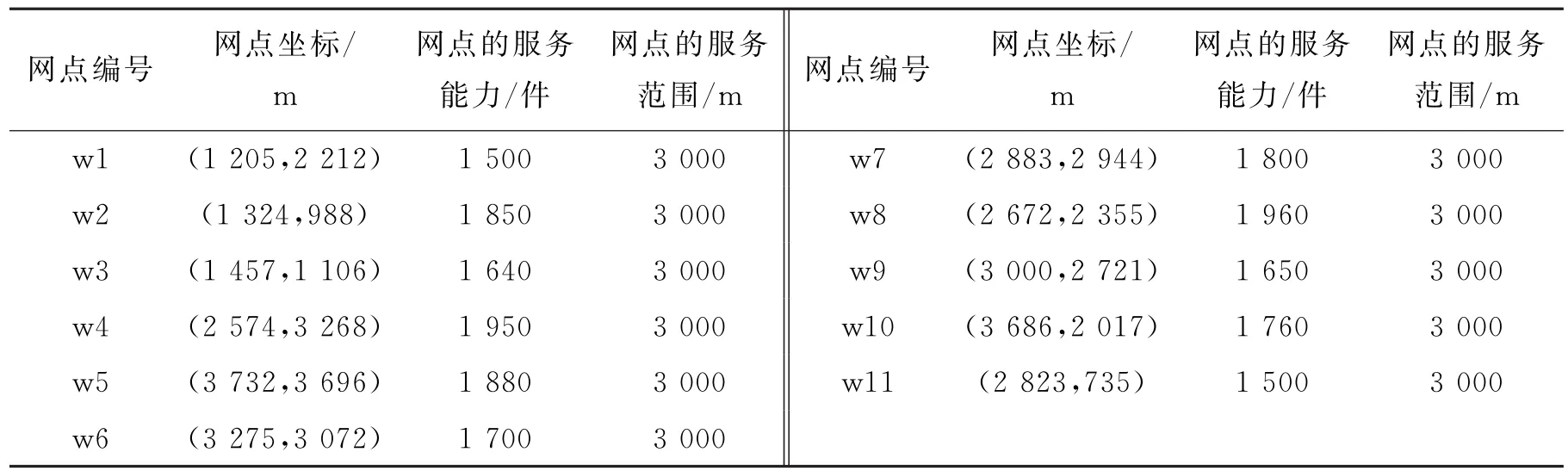
表1　现有末端网点信息

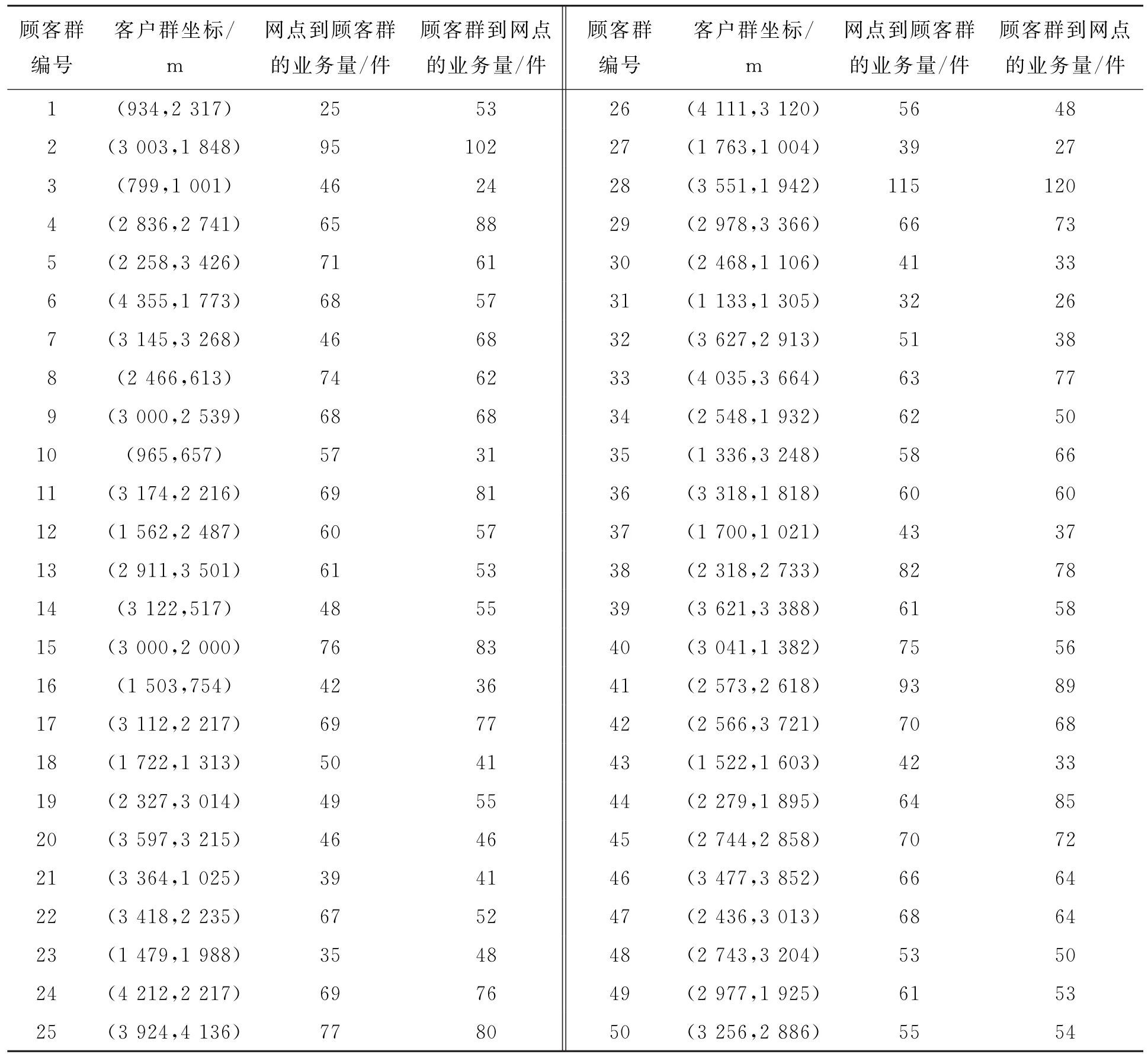
表2　顾客聚集群信息

运用MATLAB实现算法设计，计算结果如表4所示。

由表4可以看出：最优方案是使用7个网点，此时最小成本为2.995 1×109元；可保留的末端网点为w1、w2、w4、w5、w8、w10、w11（如图6所示）。

图5　现有末端网点及顾客聚集点的分布位置

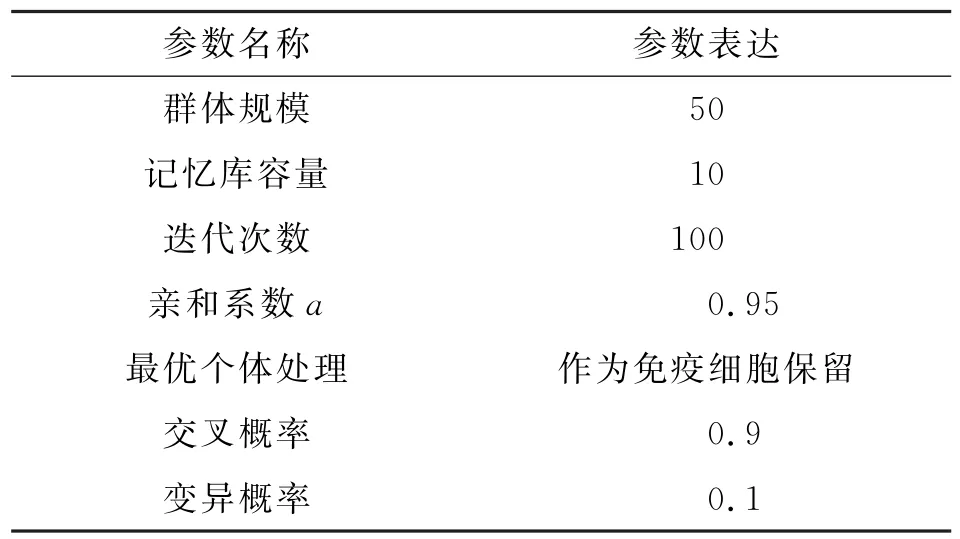
表3　免疫遗传算法的参数

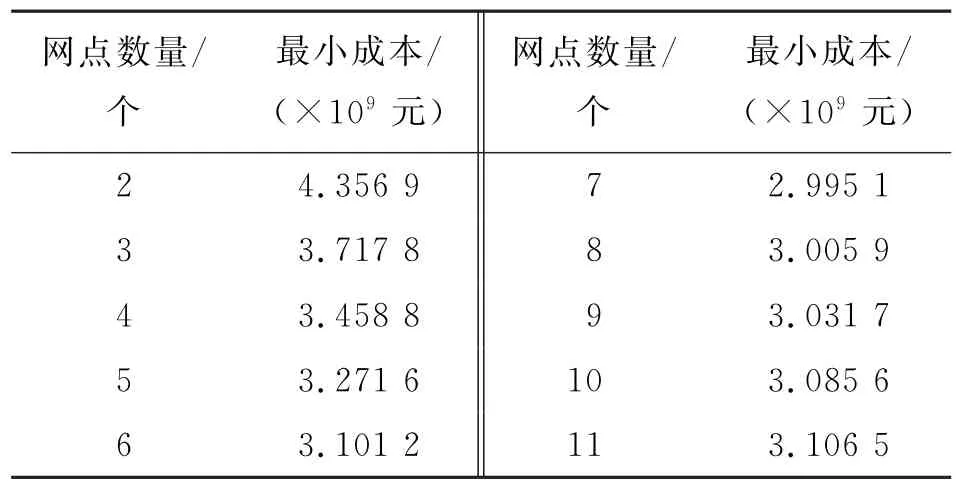
表4　模型计算结果

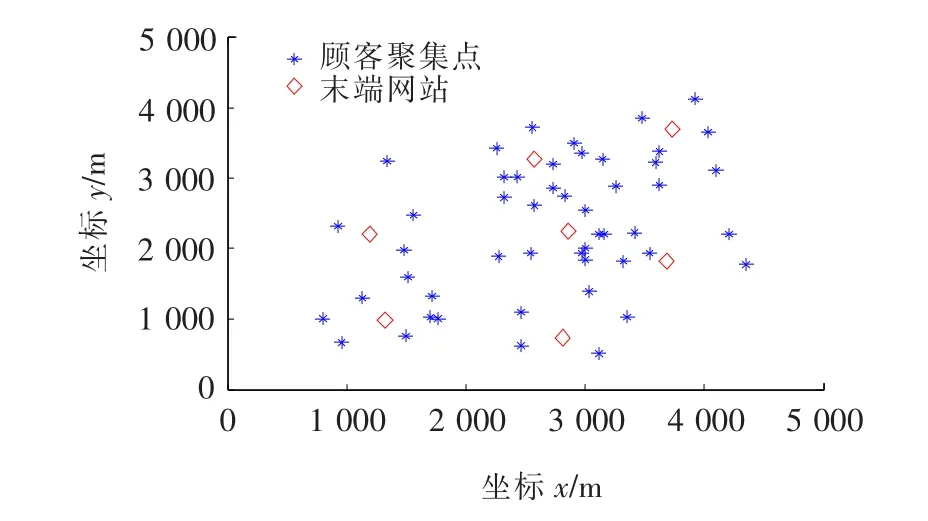
图6　保留的末端网点

5　结论

该文通过对第四方物流平台和共同配送的研究，结合快递末端网点优化整合方法，构建了基于第四方物流平台及共同配送模式的快递末端网点优化整合模型；以3家快递企业为研究对象，在满足顾客需求与系统成本最小的目标下优化整合末端网点，确定所需保留末端网点的数目及位置，提升快递服务水平，提高运作效率，有效整合快递资源。

该模型对运输费用的计算简化为两点之间的距离，而在实际中，不同的运输方式所需成本存在很大差异，即便是同一种运输方式，在不一样的规模条件下运输成本也不尽相同。因此，需进一步研究不同运输方式及同一运输方式不同规模运输成本对快递末端网点优化整合的影响。

参考文献：

［1］ 张昕.末端共同配送模式及决策路径［J］.经济问题研究，2013（3）.

［2］ 成玫颖.基于服务供应链的快递末端整合收益分配研究［D］.北京：北京交通大学，2012.

［3］ 季宬，牛孟艺，刘威志，等.大学城社区共同配送中心的配置模型［J］.中国商贸，2013，11（4）.

［4］ 张永昕.整合模式下的快递物流网络优化［D］.北京：北京交通大学，2015.

［5］ Kofi Q Dadzie，Evelyn Winston，Robert Hinson.Competing with marketing channels and logistics in africa′s booming markets：an investigation of emerging supply chain management practices in ghana［J］.Journal of Marketing Channels，2015，22（2）.

［6］ 张露方，徐杰.共同配送模式在城市电子商务末端的应用探析［J］.物流科技，2013，36（6）.

［7］ 钟耀广.电子商务城市末端配送问题与对策研究：以东莞为例［J］.物流技术，2015，34（5）.

［8］ 赵志敏.利用第四方物流平台整合快递服务资源研究［D］.北京：北京邮电大学，2012.

［9］ 张俭.快递业进入整合重组时代［J］.中国物流与采购，2012（7）.

［10］ 王琼，吕微，任伟建.免疫遗传算法及在优化问题中的应用综述［J］.计算机应用研究，2009，26（12）.

［11］ 马永杰，云文霞.遗传算法研究进展［J］.计算机应用研究，2012，29（4）.

［12］ Afshin Mehrsai，Hamid-Reza Karimi，Klaus-Dieter Thoben，et al.Using metaheuristic and fuzzy system for the optimization of material pull in a push-pull flow logistics network［J］.Mathematical Problems in Engineering，2013，2013.

［13］ 蒋尚亭.基于免疫遗传算法的高校运动会赛程编排问题研究与实现［J］.合肥学院学报：自然科学版，2014，24（1）.

参数设置：A为需要优化整合的末端网点集，i ∈A，共I个；B为顾客群聚集点的集合，j∈B，共J个；Ui为保留网点i所需固定运营成本；Fi为第i个末端网点所能接受的最大业务量；Fj为第j个客户聚集点的业务量；Fo，i为从配送中心到网点i的货运量；Fi，o为从网点i到配送中心的货运量；Fi，j为从网点i到顾客聚集点j的货运量；Fj，i为从顾客聚集点j到网点i的货运量；Co，i为从配送中心到网点i的单位货物量的成本，用两点间的距离简化表示；Ci，o为从网点i到配送中心的单位货物量的成本，用两点间的距离简化表示；Ci，j为从网点i到顾客群聚集点j的单位货物量的成本，用两点间的距离简化表示；Cj，i为从顾客群聚集点j到网点i的单位货物量的成本，用两点间的距离简化表示；

目标函数为：

中图分类号：U492.3

文献标志码：A

文章编号：1671-2668（2016）03-0079-05

基金项目：∗湖南省交通科技项目（201148）

收稿日期：2016-02-16