二层次模糊综合评判理论在桥梁震害预测中的应用

2016-06-08刘航

公路与汽运 2016年3期

关键词：模糊数学综合评价层次分析法

刘航

（陕西省交通运输厅公路处，陕西西安 710075）

二层次模糊综合评判理论在桥梁震害预测中的应用

刘航

（陕西省交通运输厅公路处，陕西西安 710075）

摘要：为评价桥梁地震安全性，基于模糊数学提出了桥梁震害等级预测模型。先将震害等级划分为基本完好、轻微破坏、中度破坏、严重破坏、倒塌5个等级，建立上部结构、场地、下部结构共3类7项指标集合；然后基于层次分析法（AHP）构权法，对二级指标采用比较矩阵特征值分析得到权重向量，而对一级指标采用专家调查法确定权重，分别应用隶属函数和经验法确定定量、定性指标的隶属度建立模糊隶属度矩阵；最后利用加权平均型算子进行模糊运算，按照最大隶属度原则对桥梁震害等级进行预测，并用其他方法验证预测结果的可靠性。

关键词：工程管理；桥梁；模糊数学；震害等级；层次分析法（AHP）；综合评价

近年来全球地壳运动进入一个异常活跃期，各国地震灾害频发。中国地处欧亚地震带中段，是地震多发地区。强震会对陆地交通运输系统、通信网络、电力系统等生命线工程产生巨大破坏。而桥梁作为交通运输系统的重要组成部分，在地震中往往会遭受不同程度的破坏，不仅阻断交通，还会给抗震救灾造成很大困难。因此，桥梁地震安全性评估是城市防震减灾重要的基础性工作之一，在交通系统防震减灾中处于核心地位。

1　桥梁地震安全性评估研究现状

桥梁地震安全性评估是指按确定的抗震设防标准，对桥梁结构在现有状况下的安全性进行评估。它是交通系统可靠性分析、损失评估及桥梁加固优先级评价和地震应急决策的重要依据。桥梁震害预测即评估桥梁结构在未来地震中的安全等级。

目前，桥梁震害预测方法大体分为经验统计法、规范校核法、结构分析法、基于遗传优化神经网络的方法和模糊综合预测法5类。本质上而言，前4类均属于确定性分析法。经验统计法简单、经济，但计算误差很大；圬工砌体采用规范校核法较为适宜；对于重要复杂桥梁结构，则应采用结构分析法如反应谱法、静动力时程反应分析法、push over法。

事实上，影响桥梁震害程度的因素具有不确定性，应用模糊数学工具评估桥梁地震安全性显得更为合理。目前，这方面的研究尚不多见，邓民宪选取桥梁宽度、场地土类型、建造年代作为指标，并建立了各指标的隶属函数，为中、小型桥梁群体震害的模糊预测奠定了理论基础；陈一平选取8个影响桥梁震害等级的主要因素，提出震害度的概念，运用模糊数学理论改进了传统的交通震害预测方法，并研发了“交通系统震害预测计算机辅助系统（DPLH）”；黄龙生选取场地液化条件、桥型、跨数组成单层次指标集，用统计回归的方法建立指标的隶属度，对大面积范围内公路桥梁可能的震害等级进行了预测。该文将层次分析法（AHP）引入桥梁震害模糊预测中，提出桥梁震害二层次模糊综合预测方法。

2　模糊综合评判理论简介

模糊综合评判决策是对受多种不确定因素影响的事物作出全面评价的一种十分有效的多因素决策方法，一般来说，当评价论域中指标特别多、指标之间的权重难以确定或评价论域中指标有多个层次、指标之间互相影响时，往往采用多层次模糊综合评价法。多层次模糊综合评价法的原理和步骤如下：

若指标集U包含n个指标，将指标集U按指标的属性类型划分为S个子集，记为U1，U2，…，Us，且满足：

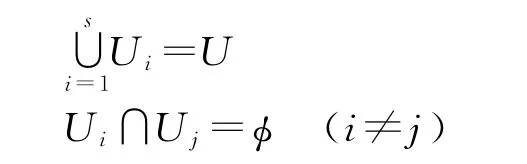
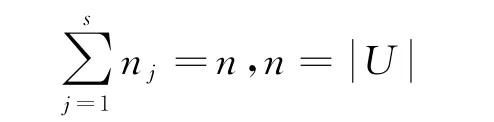
Ui的单因素评判矩阵为Ri，则第一级综合评判为：

将每个Ui作为一个元素，用Bi作为其单因素评判，则可构成评判矩阵R：

它是｛U1，U2，…，Us｝的单因素评判矩阵，可按其重要程度给出权重向量：

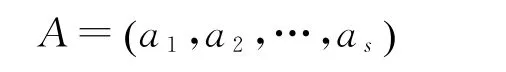
得第二级综合评判为：

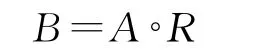
由此类推，可得到多级模糊综合评判。

3　桥梁震害二层次模糊预测模型

3.1预测指标集

模糊指标集分为两个层次，其中一级指标共3个，分别为上部结构、场地、下部结构。每个指标下又包含不同的二级指标（见图1）。

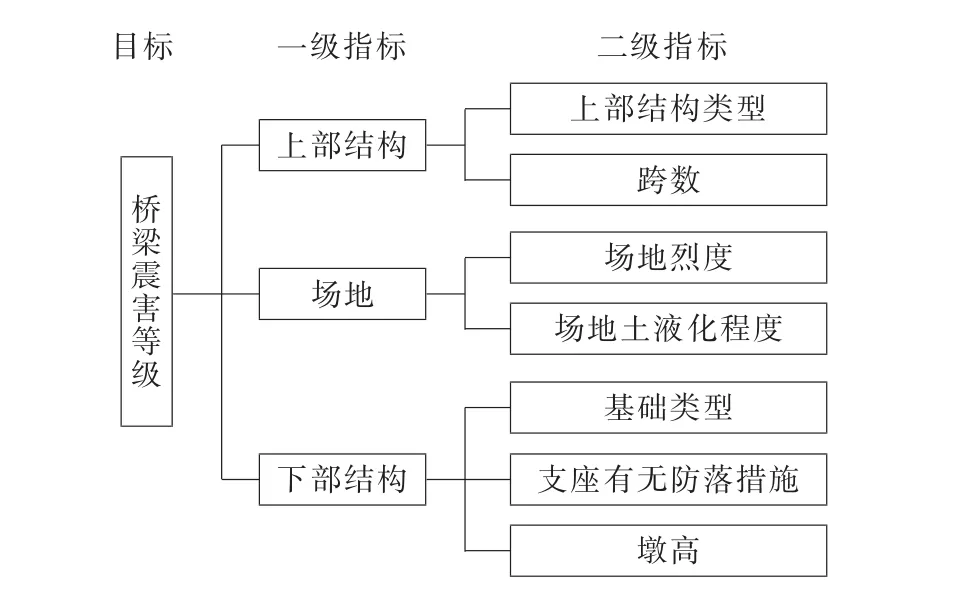
图1　桥梁震害预测二层次指标集

3.2权重向量

权重系数对模糊综合预测来说至关重要，确定方法主要有专家调查法、比较矩阵法、Delphi法、数列分析法。

一级指标权重系数的确定采用专家调查法。二级指标权重的确定采用比较矩阵法，即单准则AHP构权法，主要步骤如下：对同一层次的一级指标集Us中的n个二级指标，以上层指标Us为准则两两进行比较，并依据“1～9标度”对重要程度赋值。其中为任意两指标相对于准则Us的重要程度的标度，最后建立比较矩阵Vs如下：

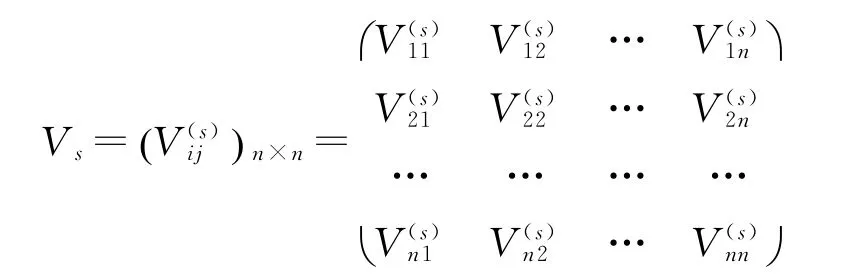
根据Vs，计算n个指标相对于准则Us的权重系数，写成向量形式为：

权重的计算方法主要有和法、方根法、特征根方法、幂法、最小二乘法等，这里采用和法。主要步骤如下：1）将判断矩阵Vs的元素按列归一化处理，得到矩阵Q=（qij）n×n；2）将矩阵Q的元素按行相加，得到向量α=（α1，α2，…，αn）T；3）对向量α作归一化处理，得特征向量；4）求最大特征值λmax。

将比较矩阵Vs写成行向量的形式：

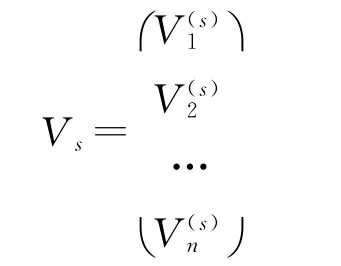
在单准则下计算权重向量时，为了得出不违反常识的正确结论，必须对比较矩阵进行一致性检验。方法如下：

（1）计算一致性指标CI：

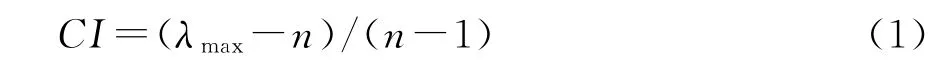
式中：λmax为比较矩阵的最大特征根；n为比较矩阵的阶数。

（2）查表求平均一致性指标RI。表1为1～14阶正互反矩阵计算1 000次得到的平均随机一致性指标。

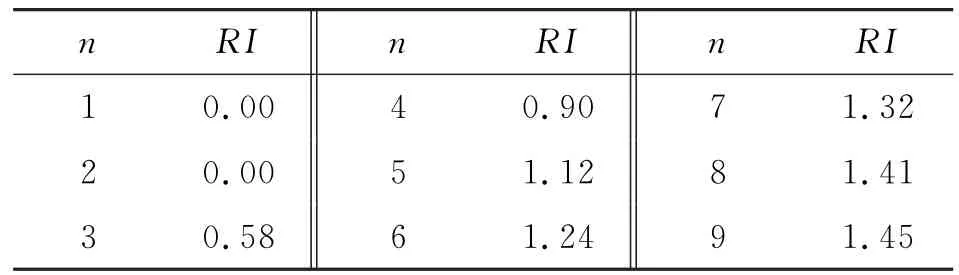
表1　平均随机一致性指标

（3）计算一致性比例CR：

若CR＜0.1，则一致性满足要求。

3.3评语等级集

在对桥梁震害进行预测时，按照惯例将震害等级划分为5级，并建立评语等级集V：

式中：vi（i=1，2，…，5）为评语等级分量，分别对应基本完好（Ⅰ级）、轻微破坏（Ⅱ级）、中等破坏（Ⅲ级）、严重破坏（Ⅳ级）、倒塌（Ⅴ级）5个等级。

3.4模糊算子

模糊运算常用算子有M（·，∨）型、M（∧，∨）型、M（∧，⊕）型和M（·，+）型4种，这里采用M（·，+）型算子。

4　工程应用

4.1工程概况

山东省某公路桥，上部结构为8×20 m钢筋砼简支实心板桥，位于直线路段。采用钢筋砼双柱式桥墩，墩高5～10 m，钻孔灌注桩基础，双排桩基，低桩承台。桥址场地为Ⅰ类，有可能发生液化，且地基土不均匀性较强，无抗液化措施。支座采用盆式橡胶支座，有防落梁措施，桥梁按JTJ 021-89《公路桥涵设计通用规范》进行了抗震设防。下面运用上述方法预测烈度为7度时该桥的震害等级。

4.2预测结果

依据前述步骤对该简支梁桥进行二层次模糊评价，得：

依据最大隶属度原则，该算例评语等级向量隶属度最高的分量为v2，该分量对应的桥梁破坏等级为轻微破坏（Ⅱ级），即可判定该桥在烈度为7度时，轻微破坏的可能性最大。

为验证该方法的正确性，分别采用朱美珍法、I. G.Buckle法对该简支梁桥进行震害预测，并把计算结果与该桥梁实际震害进行对比，结果见表2。

表2　不同方法震害预测结果对比

5　结语

该文基于模糊数学理论，提出了适合桥梁震害等级预测的二级模糊预测方法，建立了二级预测指标集。基于AHP构权准则，确定二级指标权重，按照专家调查法确定一级指标权重。定量指标利用隶属函数计算模糊隶属度，定性指标按经验法确定其模糊隶属度，采用M（·，+）算子进行模糊综合预测。结合工程实例，将多种预测方法结果进行对比，验证了模糊预测方法的可行性。

参考文献：

［1］王东升，冯启民.桥梁震害预测方法［J］.自然灾害学报，2001，10（3）.

［2］陈一平，陈欣.公路交通系统震害预测计算机辅助系统DPLH简介［J］.建筑科学，1994，10（4）.

［3］杨伦标，高英仪.模糊数学原理及应用［M］.广州：华南理工大学出版社，1993.

［4］姜淑珍，林均岐.城市桥梁震害预测方法的探讨［J］.世界地震工程，2004，20（4）.

［5］鲍卫刚，李建中，刘建新，等.积极开展公路桥梁抗震性能评价及抗震加固技术研究［J］.公路，2002（7）.

［6］黄龙生，姜淑珍.公路桥区域性震害预测［J］.地震工程与工程振动，1995（7）.

［7］郭金玉，张忠彬.层次分析法的研究与应用［J］.中国安全科学学报，2008，18（5）.

［8］邓民宪，宋龙伯.桥梁群体震害预测方法的研究［J］.地震学刊，1995（1）.

［9］孙颖，邢文杰，游福科.基于模糊层次分析法的公路梁式桥地震震害预测研究［J］.福州大学学报：自然科学版，2013，41（4）.

［10］柳春光，张利华.遗传优化神经网络方法在桥梁震害预测中的应用［J］.地震工程与工程振动，2008，28 （1）.

［11］王秋萍.汶川地震桥梁震害模糊综合评估方法研究［D］.成都：西南交通大学，2011.