基于高斯采样和随机采样聚类的差分演化算法

程　钢， 刘　罡， 胡延忠

(湖北工业大学计算机学院， 湖北 武汉 430068)

基于高斯采样和随机采样聚类的差分演化算法

程钢， 刘罡， 胡延忠

(湖北工业大学计算机学院， 湖北 武汉 430068)

[摘要]基于中心采样的概念，提出随机采样方法。研究差分演化算法，提出基于高斯采样和随机采样的聚类差分演化算法。通过实验，论证了高斯采样和随机采样显著的加快收敛速度、提升算法的求解能力，表明该算法对复杂的全局优化问题有很好地求解能力，比经典差分演化算法具有更好的求解性能。

[关键词]差分演化算法； 全局优化； 随机采样

针对全局优化问题， R.storn和K.Price提出差分演化算法(Differential Evolution，DE)，算法采用实数编码方式，其原理及演化流程与遗传算法十分相似，如父代生成子代的操作均包括变异、交叉和选择，且很好的解决了全局优化问题[1-4]。

本文提出随机采样的方法。随机采样与中心采样相比，前者因其随机性，其搜索能力更灵活、更有效。由于差分演化算法擅长全局搜索整个解空间，解的局部区域开拓相对缓慢。为了改进差分演化算法的求解性能，本文将随机采样、高斯采样和一步K均值聚类方法结合到差分演化算法中，旨在提高差分演化算法对解得局部区域的开拓能力，提出了基于高斯采样和随机采样的聚类差分演化算法(GRCDE)。

1差分演化算法

差分演化算法利用差分变异操作将种群中任意个体选取两个差分向量加权；再根据一定规则加到新的个体上，随后进入交叉操作，通过交叉系数产生新个体，该变异方式有效利用种群分布特性，提高了全局搜索能力，避免了其它演化算法中存在的变异机制不足现象；算法在选择操作上采取贪婪选择操作，选择适应值大的个体保存到下一代。

差分演化算法的关键步骤：

1)变异操作

变异操作指算法将种群中任意个体选取两个差分向量加权从上一代种群中生成新个体进入下一代。变异机制实现了对搜索空间的搜索。

在差分演化算法中，很多变异操作机制在文献[5]提出，现将一些比较知名的变异机制介绍如下：

随机差分向量法

DE/rand/1 :Vi=Xr1+F(Xr2-Xr3)

(1)

最优解加随机向量差分法

DE/best/1:Vi=Xbest+F(Xr1-Xr2)

(2)

最优解与随机向量差分法

DE/rand-to-best/1:

Vi=Xi+λ(Xbest-Xi)+F(Xr1-Xr2)

(3)

其中，Vi是目标向量，Xi是变异向量。r1，r2，r3∈{1，2,…,NP}是随机选择不同的整数且不同于运行指数i；Xbest代表目前这一代最好的个体；F(>0)变异因子；λ是增加的控制参数。

2)交叉操作

交叉操作的目的是对种群中前几代所求得的解进行重组。交叉操作对种群中的当前向量和变异向量进行重组，从而构建了新的试验向量；再经过交叉操作，通过对上一代向量和新的试验向量的适应值进行比较，两者中适应值高的进入下一代。交叉操作如下：

其中uij是试验向量。

3)选择操作

选择操作采用“贪婪”的搜索策略，经过前面两步操作后，生成的试验向量个体ui,G与目标向量个体Vi,G进行竞争，对两者中适应值相比较，更优的个体才被选中进入下一代。选择操作如

其中Xi,G+1是新的种群个体向量。

2改进的差分演化算法

2.1随机采样

中心采样是由Rahnamayan[6]提出。在搜索空间中，搜索区间的中心有很大概率接近问题的解。随机采样基于中心采样的概念，给定搜索区间[-(|a|+|b|),(|a|+|b|)],如图1所示，该区间内的随机点按式(4)所示，对于n维情况，具体如

ri=(|ai|+|bi|) rand(-1,1)

(4)

由于最优解的位置具有不确定性，为了增加包含最优解的概率，需要对搜索区间进行扩展。由于ri位于区间[-(|a|+|b|),(|a|+|b|)]内的随机性，使其在整个区间内移动。在中心采样中，ci是位于区间(ai，bi)的固定中心点。与中心采样相比，随机采样的搜索区间更大。事实上，中心采样可以被视为随机采样的子集。当rand(-1, 1)为0.5时，随机采样退化为中心采样。与中心采样使用的固定值相比，随机采样使用的随机数有更大的灵活性，使得候选解有更大的机会接近全局最优解。直观的解释如图1所示。

图 1　随机抽样图

图中x是候选解，s是全局最优解，r是搜索区间 [-(|a|+|b|),(|a|+|b|)]内产生的随机点，r=(|a|+|b|)rand(-1,1)(其中rand(-1,1)是均匀分布在(-1,1)的随机数)。

整个搜索区间[-(|a|+|b|),(|a|+|b|)]可以分为[-(|a|+|b|),r]和[r,(|a|+|b|)]两个子区间。由此可见，x和s既可能在不同子区间，也可能在同一子区间。当x和s在不同子区间时，r位于x和s之间。无论s在何位置，x和r分别到s的距离都满足‖x-s‖≥‖r-s‖。当x和s在相同的子区间时，则存在x和r一起竞争谁更接近s。由于s位置的不确定性，随机点r可能比区间[-(|a|+|b|),(|a|+|b|)]的中心点更接近全局最优解s。因此，随机采样具有更大灵活性，使得随机点r有更高的概率接近全局最优解s。

2.2随机采样的变异机制和高斯采样的变异机制

在演化阶段初期，由于种群具有较大的分布偏差，搜索过程主要集中于对整个空间的全局搜索；随着运行代数增长，分布偏差逐渐变小，搜索过程就逐步转为对局部区域的开拓。当搜索过程处于局部开拓时，使用随机采样变异机制和高斯采样变异机制对每个子种群进行搜索。随机采样和高斯采样都具备很好的局部开拓的性能。数学上表示为：

随机变异机制

(5)

高斯变异机制

(6)

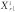
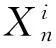
2.3基于高斯采样和随机采样聚类的差分演化算法

差分演化算法擅长全局搜索整个解空间，然而差分演化算法对解的局部区域开拓相对缓慢。为此本文将随机采样、高斯采样和一步K均值聚类方法结合到差分演化算法中，试图提高差分演化算法对局部区域的开拓能力；提出了基于高斯采样和随机采样的聚类差分演化算法(GRCDE)。在GRCDE中，使用目标空间距离测度的一步K均值聚类算法用于划分种群。利用高斯变异机制和随机变异机制分别在每个子种群中搜索新的个体。基于两种不同原理的变异机制可以有效地对子空间进行搜索，增强差分演化算法对局部区域的开拓能力。在GRCDE中，2种变异机制生成了两个新的试验向量，然后两个试验向量中最好的一个向量被用来替换子种群中的目标向量。GRCDE使用的差分演化算法变异机制采用折衷选择机制[5,7]。

具体情况如式(7)所示

Vi= Xr1+ F (Xr2- Xr3)

(7)

其中，Xr1的适应值优于Xi的适应值，r1≠r2≠r3≠i。这种算法变异机制是从当前种群中按如下要求随机选择一个个体，该个体的适应值必须优于作为变异对象的目标个体适应值。这种方法在保持收敛速率的同时，有助于维持种群的多样性。

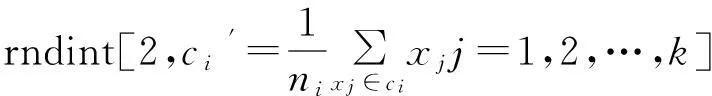
算法1：GRCDE算法

Step1：随机生成初始种群P，在种群P中对每一个个体的适应值进行评估，设置迭代计数器t=1；

Step2：当终止标准不满足继续执行；

Step3：根据Vi= Xr1+ F (Xr2- Xr3) 生成新的试验向量V={vi,1;vi,2,…,vi,D}；

Step4：依据t%m=0判断多少代进行一次聚类；

Step 6：(随机变异机制和高斯变异机制)对于第i个子种群，使用随机变异机制生成的新的个体A，同时也使用高斯变异机制生成新的个体B。在A和B通过竞争后，选取优胜者去取代第i个子种群中相应的个体。

Step 7：判断是否达到终止输出条件，满足输出结果，否则继续Step2。

在GRCDE中，种群被分成K个子种群，并且利用两种不同的变异操作机制对子种群进行开拓。多个不同的变异机制与单个的变异机制相比，可以同时搜索更多的个体。通过多个父体交叉后产生的新个体之间进行竞争比较，优胜者将被选出并进入下一代种群。这种方法提高了搜索效率并且增加了搜索到最优解的机会。

3GRCDE性能分析

3.1实验设置

针对GRCDE的性能，选取了3个演化学界常用基础函数进行测试。3个函数都是高维函数，f1是单峰函数，f2是有噪声的四次函数，f3是有很多局部最小值的多峰函数。

实验设置如下：维度D=30；种群规模NP=100；变异因子F=0.5；交叉概率因子CR=0.9；聚类周期m=MAX_NFEs(最大个体评估次数)=5000；运行次数：各种算法将每个函数运行50次。“Mean”表示在50次运行内发现了最好的适应值。“SR”表示成功运行的次数。“NFEs”是评估适应值的数量。 “MeanNFEs”表示算法的函数评估数量的平均数量成功。“Stddev”表示函数标准偏差值和最大评估适应性数量平均值。如果算法在运行50次没有1次成功，表示算法对该问题不适用，并用“N/A”表示。

(xi-1)2), -30≤xi≤30

(8)

-1.28≤xi≤1.28

(9)

-5≤xi≤10

(10)

3.2对GRCDE和DE的比较

1)比较解的精度

对于DE/rand/1,DE/best/1/和GRCDE的基础测试函数，最大评估次数MAX_NFEs=2.00E+05，并在表1中进行了总结。在图2中DE/rand/1，DE/best/1，GRCDE分别运行函数f1,f2,f3的演化过程，关于DE/rand/1,DE/best/1和GRCDE性能如图2所示。通过分析表1和图2的结果可知，在上述实验中GRCDE求解性能比DE优越。

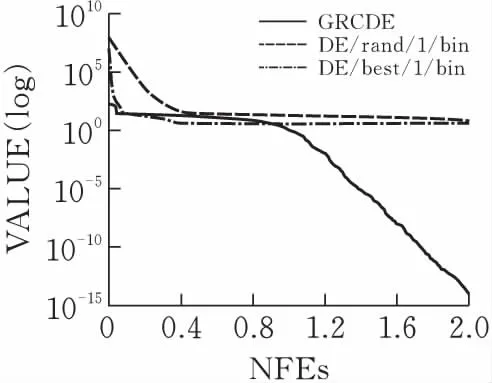
(a)函数f1

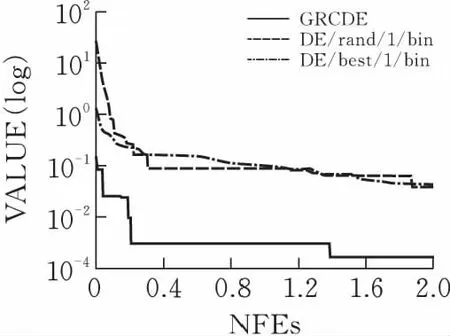
(b)函数f2

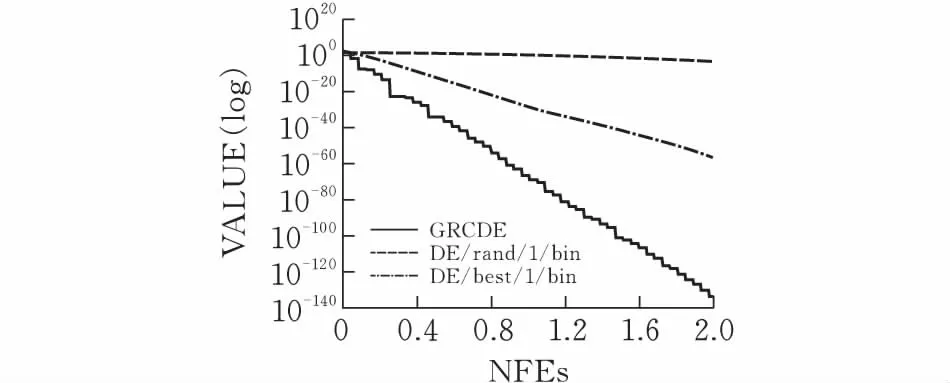
(c)函数f3图 2　算法运行几种测试函数的过程

2)比较收敛速度和成功运行的次数

由于收敛速度是算法性能一项重要指标，现比较了不同算法的收敛速度。需要对目标函数的阈值进行选择和比较，对于所有函数不同的阈值具有不同功能，表2中Threshold表示目标函数的阈值，其中f1、f3阈值设为1.00×10-10,f2阈值设为5.00×10-3。在到达终止标准时算法终止，在本节中，当最好的适应值低于预定义的阈值，或者个体评估次数的数量(NFEs)达到最大评估次数 (MAX_NFEs= 5.00×105)时，算法终止运算。

表1　所有函数最好适应值的平均值和协方差的结果

表2　在预设精度下评估次数的平均值和成功运行次数

表2中所有函数都进行50次独立的运算，然后记录收敛到阈值需要的平均个体评估次数的值和SR，其中SR是成功运行的次数。3种算法的NFEs平均值、标准偏差和成功运行次数SR，如表2所示。在表2中，所有算法的最大评估次数(MAX_NFEs)均为500,000，“N/A”代表到最大评估次数 (MAX_NFEs) 时精度水平没有达到要求。由此可见，GRCDE在3个函数中的收敛速度要比DE/best/1和DE/rand/1快，同时与差分演化算法相比，在GRCDE中NFEs的数量明显减少。

4结束语

在GRCDE中，利用高斯采样和随机采样设计两种不同的变异机制。不同的变异机制充分利用不同的搜索技术以不同的搜索方式对解空间进行搜索，这样就提高了全局搜索的效率和局部开拓的能力。值得注意的是，如果种群的规模太小，变异机制的作用会受到限制。在GRCDE中，当子种群的规模大于5时，变异机制才被用来搜索这个子种群。

实验结果表明，高斯采样和随机采样会显著加快收敛速度，提升差分演化算法的求解能力。本文提出GRCDE在对复杂的全局优化中具备很好地求解能力，这种改进的差分演化算法具有良好求解性能。

[参考文献]

[1]ReddyAS,VaisakhK.Shuffleddifferentialevolutionforlargescaleeconomicdispatch[J].ElectricPowerSystemsResearch, 2013, 96: 237-245.

[2]ZhongY,ZhangL.Remotesensingimagesubpixelmappingbasedonadaptivedifferentialevolution[J].Systems,Man,andCybernetics,PartB:Cybernetics,IEEETransactionson, 2012, 42(5): 1306-1329.

[3]ChakrabortyUK,AbbottTE,DasSK.PEMfuelcellmodelingusingdifferentialevolution[J].Energy, 2012, 40(1): 387-399.

[4]KhushabaRN,Al-AniA,Al-JumailyA.Featuresubsetselectionusingdifferentialevolutionandastatisticalrepairmechanism[J].ExpertSystemswithApplications, 2011, 38(9): 11 515-11 526.

[5]PriceKV.Differentialevolutionvs.thefunctionsofthe2ndICEO[C]//EvolutionaryComputation, 1997.IEEEInternationalConferenceon.IEEE, 1997: 153-157.

[6]RahnamayanS,WangGG.Center-basedsamplingforpopulation-basedalgorithms[C]//EvolutionaryComputation, 2009.CEC’09.IEEECongresson.IEEE, 2009: 933-938.

[7]PriceK,StornR,LampinenJ.differentialevolution-apracticalapproachtoglobaloptimization[M].BerlinGermany：Springer, 2005.

[责任编校： 张岩芳]

A Clustering Differential Evolution Algorithm Based on Random Sampling and Gaussian Sampling

CHENG Gang， LIU Gang， HU Yanzhong

(SchoolofComputerScience,HubeiUniv.ofTech. ,Wuhan430068,China)

Abstract：Based on the concept of center-based sampling, the paper proposed a method of random sampling. It studied the Differential Evolution, proposing the clustering differential evolution algorithm based on random sampling and Gaussian sampling (GRCDE). Experiment results indicate the Gaussian sampling and the random sampling remarkably accelerate the convergence rate and improves exploitation ability of DE. It shows that GRCDE has a better solving ability and our proposed GRCDE performs better than some DE variants.

Keywords：Differential Evolution, global optimization, random sampling

[收稿日期]2015-05-18

[基金项目]国家自然科学基金项目(61300127)

[作者简介]程钢(1983-)， 男， 湖北洪湖人，湖北工业大学硕士研究生，研究方向为差分演化算法，图论

[文章编号]1003-4684(2016)02-0045-03

[中图分类号]TP301.6

[文献标识码]：A