基于近似集与粒子群的粗糙熵图像分割方法*

姚龙洋，张清华,+，胡帅鹏，张　强



基于近似集与粒子群的粗糙熵图像分割方法*

姚龙洋1，张清华1,2+，胡帅鹏1，张强2

1.重庆邮电大学计算智能重庆市重点实验室，重庆400065 2.重庆邮电大学理学院，重庆400065

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(05)-0699-10

http://www.ceaj.org Tel: +86-10-89056056

* The National Natural Science Foundation of China under Grant Nos. 61472056, 61309014, 61300059 (国家自然科学基金); the Natural Science Foundation of Chongqing under Grant Nos. cstc2012jjA40032, cstc2013jcyjA40063 (重庆市自然科学基金).

Received 2015-06,Accepted 2015-08.

CNKI网络优先出版: 2015-08-13, http://www.cnki.net/kcms/detail/11.5602.TP.20150813.1108.002.htm l

YAO Longyang, ZHANG Qinghua, HU Shuaipeng, et al. Rough entropy for image segmentation based on approximation sets and particle swarm optim ization. Journal of Frontiers of Com puter Science and Technology, 2016, 10(5): 699-708.

摘要：基于经典粗糙集理论的图像分割方法缺少对目标图像不确定性边界域的精确划分，其根据先验粒度构建的图像粗糙集信息系统，并没有客观准确地反映出不同粒度之间的粗糙性信息。基于粗糙集近似集理论模型，首先采用自适应粒化方法得到图像的最优粒度，接着基于该粒度划分构建图像的目标和背景的上下近似集，再根据近似集思想对目标集合的边界域进行精确刻画，同时结合粒子群算法提高求解粗糙集近似集最大粗糙熵的效率，最终得到图像分割的最优分割阈值，并通过仿真实验表明该方法具有可行性和有效性。

关键词：图像分割；粗糙集；近似集；粒计算；粒子群

1 引言

图像分割是指根据灰度、色彩、形状、纹理等特征将一幅图像划分为互不相交的区域，从而获得图像中感兴趣的目标区域[1]。作为图像处理和计算机视觉等领域中的关键步骤，图像分割效果的好坏对图像分析和图像理解等基础环节有着直接的影响。近些年，随着越来越多的图像分割方法和技术被提出，这些方法在实际中也已得到了广泛应用，如工业制造、生物医学、机器人视觉和地理测绘等领域[1-2]。

现有的图像分割方法主要包括阈值分割法、边缘检测法、区域分割法、聚类分割法和基于特定理论的分割方法等，其中阈值分割法因其实现简单、高效稳定等特点受到了广泛关注和研究[1-2]。基于阈值的图像分割方法的基本思想是通过计算图像的特征描述信息建立直方图，选取一个或多个灰度阈值对图像进行分割，最终得到目标区域和背景区域。阈值分割法的关键就是如何选取分割阈值，文献[3]提出了最大类间方差法，它是一种无参数并且无监督的基于直方图的经典分割方法，但当直方图信噪比较低时去噪效果较差。文献[4]提出的最大熵阈值法在计算过程中无需先验知识且适用于非理想双峰直方图的图像分割，但存在多阈值计算量偏大和分割结果不稳定等问题。文献[5]提出的最小误差法通过目标与背景的灰度分布建立混合高斯模型，将二值化问题转化为最小误差化的高斯分布拟合问题。文献[6]根据计算阈值所依据的图像信息分类情况，总结并分析了近40种经典的阈值分割方法。文献[7]针对目标与背景之间不易区分的过渡区域，通过引入粗糙集理论将不确定区域转化为粗糙集的上下近似描述，提出了基于粗糙集模型的粗糙熵图像分割方法。文献[8]利用变精度粗糙集模型与遗传算法，在提高粗糙熵的求解效率的同时通过精度调节得到分割阈值。

上述方法虽然针对图像阈值分割在不同维度、计算复杂度及分割效果上进行了改进和创新，但在利用粗糙集的图像阈值分割方法过程中，图像粒度的划分仍需要人为设定，以致不能根据实际图像信息在自适应的条件下达到最优粒度。基于经典粗糙集图像分割方法在构造上下近似集描述的同时仍缺少对边界域的刻画，无法找到目标区域的最优近似[9-10]。本文提出了一种基于粗糙集近似集模型的图像分割方法，通过局部灰度方差得到自适应最优粒度，在求解图像的近似集粗糙熵过程中结合粒子群算法，最终得到给予粗糙熵的图像分割阈值。

本文组织结构如下：第2章主要介绍了粗糙集理论和粗糙集的近似集扩展模型的相关概念，以及图像的粗糙集表示；第3章给出了基于粗糙集近似集的图像粒度划分适应方法和图像的近似集粗糙熵度量，并提出了基于粗糙集近似集与粒子群算法的图像分割方法；第4章进行了对比实验，证明了本文算法的可行性和有效性；第5章是结束语。

2 相关概念

2.1粗糙集理论

粗糙集（rough set）理论是波兰数学家Paw lak于1982年提出的一种处理模糊和不确定知识的数学工具[9-10]。该理论最大的特点是不需要任何先验知识，直接从数据中提取规则，因此它在模式识别、机器学习和专家系统等多个领域得到广泛的应用[11-12]。为了更清楚地描述，首先给出粗糙集的相关基本概念。

定义1（信息系统）[9-10]一个信息系统S可以表示为。其中，U是对象全集，也称为论域；A=C⋃D是属性全集，子集C和D分别称为条件属性集和结果属性集；是属性值的集合，Vr表示属性r∈A的属性值范围，即属性r的值域；f: U×A→V是一个信息函数，它指定U中每一个对象x的属性值。

定义2（不可分辨关系）[9-10]对于任一属性集合R⊆A，定义一个不可分辨二元关系

定义3（上近似集（upper approximation set）与下近似集（lower approximation set））[9-10]给定信息系统，对于任一对象集合X⊆U和属性集合R⊆A，X关于R的上近似集(X)和下近似集(X)分别定义为：

定义4（粗糙度）[9- 10]在给定的信息系统中，IND(B)是U上的一个不可分辨关系，[x]B表示对象x的等价类，对象子集X⊆U，X的粗糙度ρB(X) 定义如下：

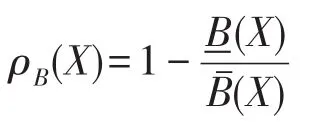
由以上定义可知，粗糙集以不可分辨关系为基础，并在此基础上定义上下近似集来近似刻画目标集合。

2.2粗糙集近似集模型

粗糙集虽然通过定义上下近似集来描述目标集合的上下边界，但是如何在当前的划分空间中利用现有粒度构造目标集合较好的近似集是值得人们关注的问题，许多学者对此进行了深入研究。文献[13]首先提出了变精度粗糙集模型，极大地促进了粗糙集在应用上的发展。文献[13]和文献[14]分别基于依赖关系和粗糙隶属度函数与粗糙包含函数研究了概率粗糙集模型，均取得了较好的结论。文献[15]提出了粗糙集近似集模型，很好地解决了目标集合的近似集构建问题。粗糙集近似集利用集合的相似度首先将粗糙集转换为模糊集，然后根据粗糙集边界域中元素的隶属度不同，利用截集的思想来构造近似集，进而基于该近似集来获取在当前粒度下的近似规则。同时，该模型已经证明当集合隶属度取0.5时的优越性[15]，由此给出目标概念的近似集。

定义5（隶属度函数）[9-10]设U是非空对象集，知识空间为U/IND(R)，对象子集X⊆U，则对于任意的，x属于集合X的隶属函数为：

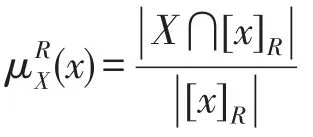
定义6（X的λ近似集）[15]设X是论域的一个集合（目标概念），令：

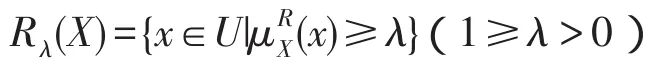
称Rλ(X)为X的λ近似集。

显然，R1(X)=-R(X)，R0(X)=(X)，即上近似集和下近似集是Rλ(X)的特例，粗糙集近似集模型是粗糙集模型的推广。文中，λ一般取0.5，如无特殊说明，粗糙集的近似集均指R0.5(X)。R0.5(X)对集合的交、并、补运算有如下性质。

性质1[15]设X、Y是两个集合（概念），则

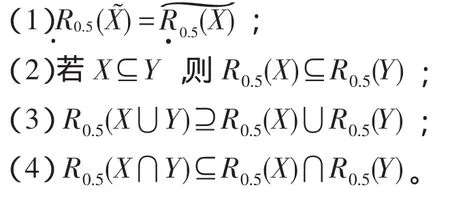
定义7（集合的近似度（或相似度））[15]设A、B是有限论域U上的两个子集，即A⊆U，B⊆U，定义映射S: U×U→[0,1]，即(A,B)→S(A,B)，如下：

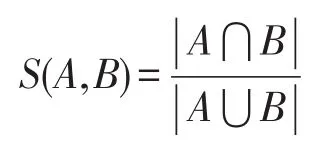
其中，||·表示有限子集的元素个数；S(A,B)是集合A、B的近似度。

定理1[15]设论域U是一个有限论域，X⊆U，R 是U上的等价关系，则S(X,R0.5(X))≥S(X,-R(X))。

定理2[15]设论域U是一个有限论域，X⊆U，R 是U上的等价关系，若

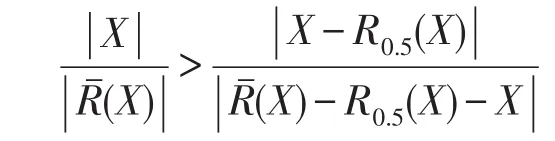
则S(X,R0.5(X))≥S(X,(X))。

定理1和定理2表明粗糙集近似集对于目标集合的近似度均高于上近似集和下近似集，这也是本文基于该模型研究图像阈值分割方法的意义所在。

2.3图像的粗糙集表示

图像信息本身所具有的相关性和不确定性等特点，造成了在图像处理过程中各个层次可能出现不完整和不精确的问题，因此通过将粗糙集理论应用到图像处理中，利用粗糙集中的不可分辨关系、近似集合概念和知识约简等思想，具有比传统模型方法和算法更完备的处理结果[16-19]。图像的粗糙集表示的基本思路是，将图像所表达的信息转化为由二维图像灰度值对象所组成的一个信息表达系统，再根据粗糙集的不可分辨关系构建该信息系统的目标与背景近似集合[7,20]。

令集合R表示整个图像区域，那么可以将图像分割看成是将R划分成n个子区域R1,R2,…,Rn的过程，如下定义，对于∀i,j且i≠j：

（2）Ri是一个连通的区域；

（3）Ri⋂Rj=∅，即任意两个子区域不存在公共元素；

（4）区域Ri满足一定的均匀性条件。

文献[7]定义了图像的粗糙集表示方法，在图像分割过程中，一幅图像的所有像素点构成论域U，将该图像划分成k个大小为m×n且互不相交的子域，其中每个子域被看作是图像粒化后的粒，记作Gi(1,2,…,k)。设有大小为M×N的图像U，灰度级为L，U上的映射g:U→{ 0,1,…,L-1}为任意像素点P处的灰度值，记作g(P) ，其中灰度值在{0,1,…,T}范围的像素组成图像的背景区域BT，而灰度值在{T+1,T+2,…,L-1}范围的像素组成图像的目标区域OT。根据粗糙集理论可得到目标和背景区域的上下近似集T、T和T、T。其中：

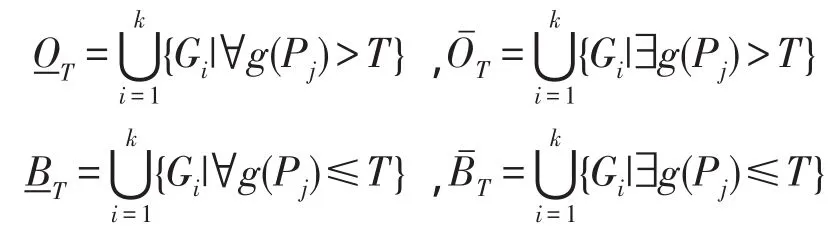
3 粗糙集近似集的图像分割方法

图像粗糙集描述的目标和背景边界域是图像分割的关键所在，与此同时，图像的粒度划分又影响着目标集合对边界域的近似刻画，因此图像粒度大小的设定以及当前粒度划分下对目标集合近似刻画将是基于粗糙集近似集理论的图像分割方法研究的重点[18-21]。

3.1图像的粒度划分

粗糙集理论模型通过定义上近似集和下近似集来逼近所描述的目标集合，即用精确的区域去近似不精确的区域，这对于不精确区域的刻画是有局限性的。被刻画的目标区域的边界域的宽窄和近似精度随论域划分的粒度的变化而变化，如果图像划分粒度较粗，则边界域较宽，近似精度也相对较低，反之亦然[15-16]。如图1所示，黑色区域为目标图像，浅灰色为粗糙集下近似区域，深灰色与阴影为边界域，在粗糙集近似集模型中，通过对边界域进行刻画构造近似目标区域，同时，粗糙集近似集构造出的目标区域又随粒度变化，不断近似逼近目标图像。

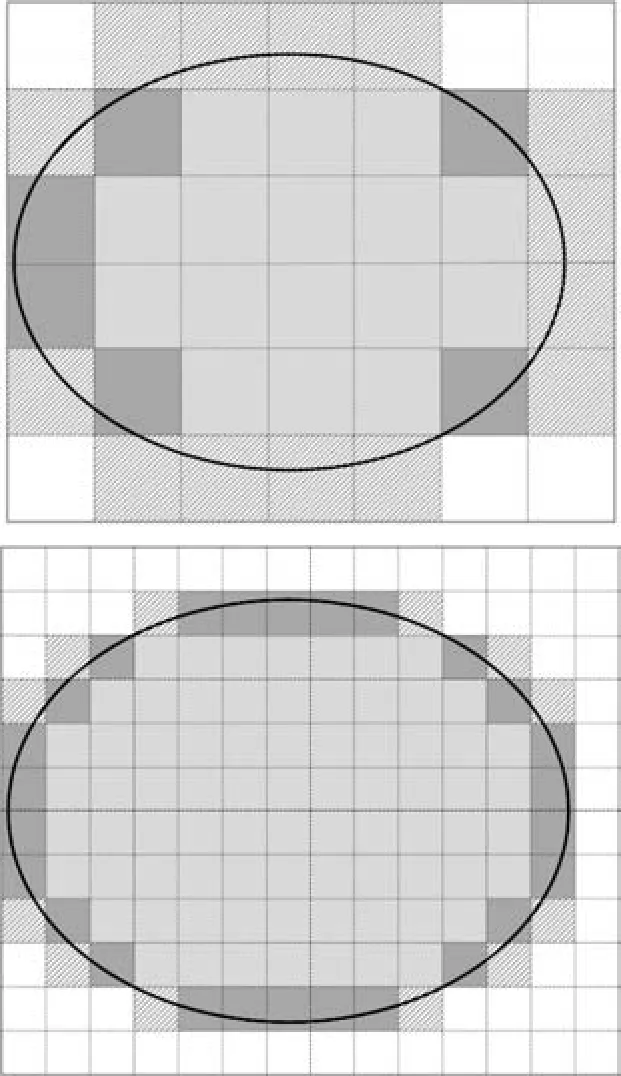
Fig.1　Evolution under different granularity of R0.5(X)图1　R0.5(X)随粒度细化的变化图

由图1分析可得，随着图像粒度的细化，得到的目标区域图像越精确。同时为了保证图像粒化后集合的粗糙性和关联性，粒度的划分不能过小，因此如何找到图像的最优粒度划分就成为图像粗糙集近似集表示的关键。

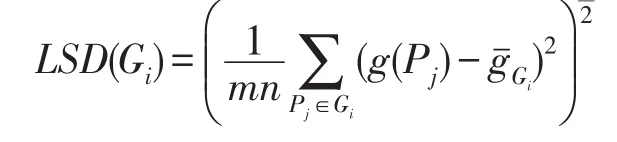
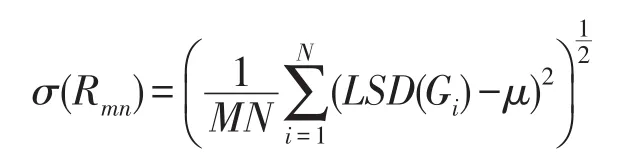
3.2图像的粗糙熵度量

由粗糙集近似集理论，当R0.5(X)作为目标集合的近似集要优于上下近似集，给定一幅图像记作F，其中X={P∈Gi|F(P)>T}，则目标和背景区域的近似集合区域表示如下：

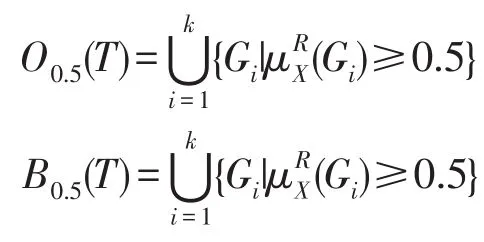
由近似区域定义可看出，目标区域的近似集是图像F灰度值大于T的像素集合且不小于0.5隶属度的粒度集合，背景区域表示F中满足灰度值不大于T的像素集合且不小于0.5隶属度的粒度集合。当μ=1时，目标和背景集合区域回归至经典粗糙集图像表示。

由粗糙集粗糙度公式可得到目标与背景的近似粗糙度：

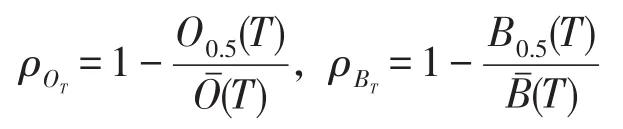
给定图像F，F的分割阈值为T，得到F的粗糙集近似集粗糙熵为:

文献[7]指出，当给定图像的粗糙熵ET取最大值时，可以得到图像分割的最佳阈值T*，同时图像的粗糙熵ET随着目标和背景区域的粗糙度ρOT、ρBT减小而增大。

3.3结合近似集粗糙熵与粒子群算法的图像分割

对于计算图像粗糙熵的求解最优解问题，文献[7]等采用穷举法求得，但该算法的求解效率明显偏低。文献[8]在求解过程中采用遗传算法来提高求解效率，并获得了明显的效果。

本文在基于粗糙集近似集图像分割过程中，通过引入粒子群算法来进一步改善粗糙熵最优解。相较于遗传算法的迭代规则，粒子群算法凭借更为简单的适应度评价标准，在寻找最优解的实际问题中具有更快的收敛性和较好的求解精度[25-26]。

给定大小为M×N的图像F，则基于粗糙集近似集和粒子群算法的图像分割算法描述如下：

输入：大小为M×N的图像F。

输出：图像F的分割图像和最优分割阈值T。

步骤1根据图像粒度适应准则，对图像F进行最优粒度划分，得到粒度窗口为m×n。

步骤2建立图像论域U上的等价关系Rmn，得到图像的划分粒度Gi(1,2,…,k)。

步骤3设定粒子数量为N，活动范围为[0～255]，将粗糙集近似集的粗糙熵作为适应度函数，随机初始化粒子群。

步骤4由粒子位置T∈{0,1,…,L-1}，构建图像的目标与背景上下近似集(T) 、(T)和(T) 、(T)，以及目标集合的近似集O0.5(T)、B0.5(T)。

步骤5计算每个粒子的适应值，判断迭代次数

1是否达到最大值，若达到，则将最大适应度值的粒子作为分割阈值T，执行步骤7。否则，转为步骤6。

步骤6更新粒子的位置和速度，返回步骤4。

步骤7由最佳分割阈值T输出图像分割结果。

通过以上算法描述，得到基于粗糙集近似集的图像分割阈值，在此阈值基础上对图像进行阈值分割计算，得到目标区域图像。

4 实验分析

为了验证本文算法的可行性和有效性，实验选用了Berkeley Segmentation Dataset中的测试数据，实验环境为I3-2350M CPU，2 GB RAM，W indows7操作系统，开发环境为Matlab 7.0。记图2的4幅测试图像依次为IMG1～IMG4。实验首先采用同样是基于粗糙集粗糙熵的Pal算法与本文基于粗糙集近似集的粗糙熵粒子群图像分割算法进行对比，然后使用非粗糙集模型的经典图像阈值分割算法与本文算法比较分割效果。

Fig.2 Original images图2 原始图像

4.1近似集的粗糙熵粒子群算法与传统粗糙集图像分割算法实验对比

Pal算法是基于传统粗糙集粗糙熵图像分割的经典算法，主要思想是构建图像粗糙集信息系统，通过遍历最大粗糙熵求解最佳阈值[7-8]。本文算法分别与Pal算法在分割结果、求解效率和分割阈值上进行比较。实验设置本文算法在粒子群求解过程中的初始化随机粒子数量为10。

由图3（a）与图3（b）的效果对比可以看出，本文算法与Pal方法总体上效果近似，其中IMG2和IMG3的目标图像呈现出较好的效果。因此基于粗糙集近似集模型的分割方法，对目标图像的近似性和连贯性要优于Pal算法。由表1和表2可明显得出，相较于Pal算法的穷尽方法，本文算法通过引入粒子群算法，在求解最佳粗糙熵时间开销上要优于Pal算法。图4为粒子群算法求解IMG1粗糙熵的迭代过程。4.2近似集的粗糙熵粒子群算法与其他算法对比

Fig.3 Image segmentation result between Pal and thispaper algorithms图3 Pal算法与本文算法图像分割效果对比

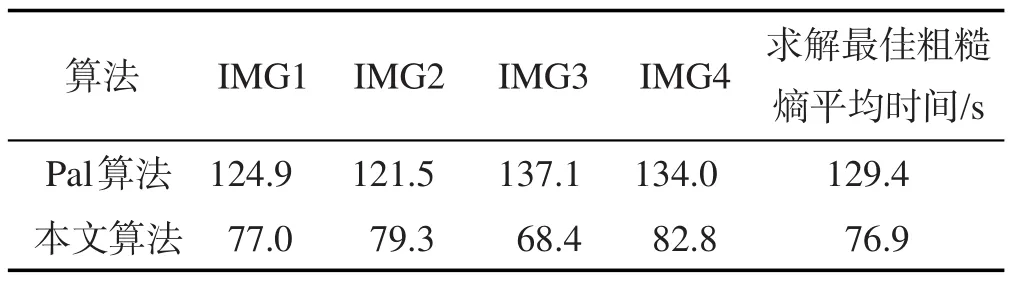
Table 1 Comparison of computing time of best rough entropy between Pal and this paper algorithms表1 Pal算法与本文算法求解最佳粗糙熵时间对比

Table 2 Comparison of solving threshold between Paland this paper algorithms表2 Pal算法与本文算法求解图像分割阈值对比

Fig.4 Iterative process of computing the maximum rough entropy of IMG1 based on PSO图4 求解IMG 1粗糙熵过程粒子群迭代过程

分别采用了最大类间方差Otsu算法、直方图最大熵Kapur算法与本文算法对选取的2幅图像进行对比实验。Ostu算法基于最小二乘法原理，通过构建图像双峰的直方图对目标图像进行分割。Kapur算法基于经典Shannon熵，通过计算一维直方图最大熵求解图像分割阈值。

由图5的分割效果可得，本文算法与Otsu算法相比较对目标图像的刻画更为明显，要优于Otsu的分割效果。本文算法与Kapur算法的结果相比较，分割效果基本近似。

基于粗糙集近似集的图像分割方法从原理上保证分割图像轮廓较好，需要先将图像转化为粗糙集信息系统，才能求解粗糙熵，因此与非粗糙集模型图像分割算法相比，基于粗糙集模型的图像分割算法在时间复杂度上可能高于Otsu算法和Kapur算法，但它提供了新的研究尝试，在后继工作中可以引入并行计算模式来提高计算效率，保证图像分割的质量和效率。

Fig.5 Comparison of image segmentation effectiveness based on Otsu, Kapur and this paper algorithms图5 Otsu算法、Kapur算法与本文算法图像分割效果对比

4.3图像分割结果的定量评价对一幅图像分割结果的好坏，通常情况下是以人的主观视觉判断作为评价标准。然而由于人类个体间视觉差异的存在，图像分割结果的评价很难从客观上得到统一。因此，为了正确评测分割算法的效果，改善分割算法的质量，图像分割需要从实际目标出发，引入客观、统一的图像分割评价方法和标准。

本文针对以上对比实验得到的不同分割结果，在算法时间复杂度和主观表现效果的基础上，参考文献[27]的图像分割评价方法，基于图像分割的模糊度量，进一步引入图像的模糊熵作为分割结果的定量评价标准。模糊集的一维模糊熵为：

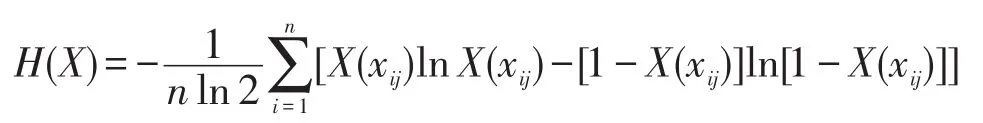
由一维模糊熵推广到二维图像模糊熵：

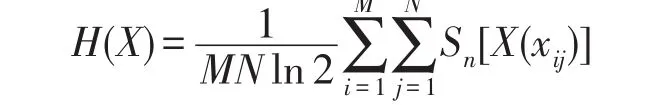
Sn[X(xij)]=-X(xij)ln X(xij)-[1-X(xij)]ln[1-X(xij)]

根据不确定性问题的模糊熵性质可知，对于图像的目标和背景进行分割结果模糊度量，当分割效果较好时，分割结果应测得较小的模糊熵。以IMG1～IMG4的图像分割结果为测试样本，分别计算本文算法与传统粗糙集图像分割算法的模糊熵，并进行对比。

由表3图像分割评价结果可得出，基于近似集与粒子群图像分割方法，图IMG1和IMG4的模糊熵基本接近，而图IMG2、IMG3的模糊熵明显低于传统粗糙集的图像分割方法，这客观反映了本文分割方法的有效性，也显出了基于模糊熵的定量评价与主观结果判断基本一致。综合可得，基于近似集与粒子群算法的粗糙熵图像分割方法，在图像分割效果和执行效率方面均优于传统粗糙集图像分割方法。

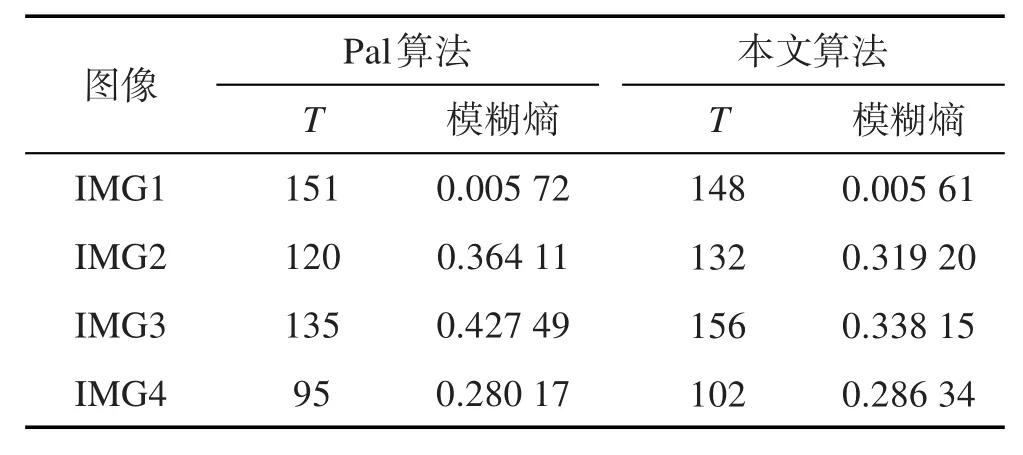
Table 3 Comparison of image segmentation effectivenessbased on fuzzy entropy evaluation between Pal andthis paper algorithms表3 Pal算法与本文算法图像分割模糊熵定量评价对比

5 结束语

作为图像处理和计算机视觉领域中的重要基础内容之一，图像分割方法一直以来都被广泛地讨论和研究，其中对于图像边界域的不确定性处理更是研究中的重点和难点问题。作为粒计算的重要模型，粗糙集理论可以通过确定性方法实现对不确定性问题进行描述和处理，并已经成功地应用于各个领域，包括人工智能、金融决策以及工业控制等。与此同时，粗糙集理论也被引入图像处理领域，尤其是在图像分割方法的研究中，为处理图像中的不确定性问题提供了可靠的理论基础和有效的处理手段。

然而，在实际的理论分析中，经典粗糙集理论缺少对目标概念的精确或近似的刻画，仅依靠传统的上下近似集并不能最大限度地对目标集合进行有效描述。因此，凭借粗糙集近似集模型对边界区域进行近似刻画具有较好的处理能力。本文基于粗糙集近似集的理论模型，提出了基于粗糙集近似集与粒子群算法的粗糙熵图像分割方法。首先将图像进行自适应最优粒化，在该粒度划分下，构造图像的目标和背景的上下近似集及其近似集图像信息系统，结合粒子群算法提高了粗糙熵计算效率，通过计算最大化粗糙熵得到图像分割的最优阈值，并通过对比实验验证了本文方法与经典粗糙集图像分割方法相比具有较好的效果和明显的时间优势，与传统经典算法的对比实验显示出了理想的效果。本文算法的提出进一步促进了粗糙集近似集模型的应用，对基于图像阈值的图像分割方法进行了扩充和发展。在未来的工作中将继续研究基于粗糙集模型的多阈值分割方法以及通过并行计算进行图像分割。

References:

[1] Xu Xinzheng, Ding Shifei, Shi Zhongzhi, et al. New theories and methods of image segmentation[J]. Acta Electronica Sinica, 2010, 38(2A): 76-82.

[2] Li Weibin, Gao Er, Song Songhe. A global m inim ization method for image segmentation[J]. Journal of Electronics & Information Technology, 2013, 35(4): 791-796.

[3] Otsu N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66.

[4] Kapur J N, Sahoo P K, Wong A K C. A new method for gray-level picture thresholding using the entropy of the histogram[J]. Computer Vision, Graphics, and Image Processing, 1985, 29(3): 273-285.

[5] Kittler J, Illingworth J. M inimum error thresholding[J]. Pattern Recognition, 1986, 19(1): 41-47.

[6] Sezgin M, Sankur B. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging, 2004, 13(1): 146-165.

[7] Pal S K, Shankar B U, Pabitra M. Granular computing, rough entropy and object extraction[J]. Pattern Recognition Letters, 2005, 26(16): 2509-2517.

[8] Deng Tingquan, Sheng Chundong. Image threshold segmentation based on entropy of variable precision rough sets and genetic algorithm[J]. Control and Decision, 2011, 26 (7): 1079-1082.

[9] Paw lak Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356.

[10] M iao Duoqian, Wang Jue. An information representation of the concepts and operations in rough set theory[J]. Journal of Software, 1999, 10(2): 113-116.

[11] Phophalia A, M itra S K, Rajwade A. Object boundary detection using rough set theory[C]//Proceedings of the 2013 4th National Conference on Computer Vision, Pattern Recognition, Image Processing and Graphics, Jodhpur, India, Dec 18-21, 2013. Piscataway, USA: IEEE, 2013: 1-4.

[12] Kuang Yubin, Byröd M, Astrom K. Supervised feature quantization w ith entropy optim ization[C]//Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops, Barcelona, Spain, Nov 6-13, 2011. Piscataway, USA: IEEE, 2011:1386-1393.

[13] Ziarko W. Variable precision rough set model[J]. Journal of Computer and System Sciences, 1993, 46(1): 39-59.

[14] Yao Yiyu. Probabilistic rough set approximations[J]. International Journal of Approximate Reasoning, 2008, 49(2): 255-271.

[15] Zhang Qinghua, Wang Guoyin, Xiao Yu. Approximation sets of rough sets[J]. Journal of Software, 2012, 23(7): 1745-1759.

[16] Chen Hongmei, Li Tianrui, Ruan Da. A rough-set-based incremental approach for updating approximations under dynam ic maintenance environments[J]. IEEE Transactions on Know ledge and Data Engineering, 2013, 25(2): 274-284.

[17] Wu Weizhi, Leung Yee, Shao M inwen. Generalized fuzzy rough approximation operators determined by fuzzy implicators[J]. International Journal of Approximate Reasoning, 2013, 54(9): 1388-1409.

[18] Liang Jiye, Qian Yuhua. Axiomatic approach of know ledge granulation in information system[C]//LNCS 4304: Proceedings of the 19th Australian Joint Conference on A rtificial Intelligence, Hobart, Australia, Dec 4-8, 2006. Berlin, Heidelberg: Springer, 2006: 1074-1078.

[19] Feng Tao, M i Jusheng, Zhang Shaopu. Belief functions on general intuitionistic fuzzy information systems[J]. Information Sciences, 2014, 271: 143-158.

[20] Hassanien A E, Abraham A, Peters J F, et al. Rough sets and near sets in medical imaging: a review[J]. IEEE Transactions on Information Technology in Biomedicine, 2009, 13(6): 995-968.

[21] Wu Tao. Adaptive rough entropy method for image thresholding[J]. Journal of Image and Graphics, 2014, 19(1): 1-10.

[22] Long Jianwu, Shen Xuanjing, Chen Haipeng. Adaptive minimum error thresholding algorithm[J]. Acta Automatica Sinica, 2012, 38(7): 1134-1144.

[23] Krinidis S, Chatzis V. A robust fuzzy local information C-means clustering algorithm[J]. IEEE Transactions on Image Processing, 2010, 19(5): 1328-1337.

[24] Zhao Xuemei, Li Yu, Zhao Quanhua. Image segmentation by fuzzy clustering algorithm combining hidden Markov random field and Gaussian regression model[J]. Journal of Electronics & Information Technology, 2014, 36(11): 2730-2736.

[25] Nosrati M S, Hamarneh G. Local optim ization based segmentation of spatially-recurring, multi-region objects with part configuration constraints[J]. IEEE Transactions on Medical Imaging, 2014, 33(9): 1845-1859.

[26] Qi Chengm ing. Maximum entropy for image segmentation based on an adaptive particle swarm optim ization[J]. Applied Mathematics & Information Sciences, 2014, 8 (6): 3129-3135.

[27] Hou Gexian, Bi Douyan, Wu Chengke. Researches on evaluation methods for image segmentation[J]. Journal of Image and Graphics, 2000, 5(1): 39-43.

附中文参考文献：

[1]许新征,丁世飞,史忠植,等.图像分割的新理论和新方法[J].电子学报, 2010, 38(2A): 76-82.

[2]李伟斌,高二,宋松和.一种全局最小化的图像分割方法[J].电子与信息学报, 2013, 35(4): 791-796.

[8]邓廷权,盛春冬.结合变精度粗糙熵和遗传算法的图像阈值分割方法[J].控制与决策, 2011, 26(7): 1079-1082.

[10]苗夺谦,王珏.粗糙集理论中概念与运算的信息表示[J].软件学报,1999, 10(2): 113-116.

[15]张清华,王国胤,肖雨.粗糙集的近似集[J].软件学报, 2012, 23(7): 1745-1759.

[21]吴涛.图像阈值化的自适应粗糙熵方法[J].中国图象图形学报, 2014, 19(1): 1-10.

[22]龙建武,申铉京,陈海鹏.自适应最小误差阈值分割算法[J].自动化学报, 2012, 38(7): 1134-1144.

[24]赵雪梅,李玉,赵泉华.结合高斯回归模型和隐马尔可夫随机场的模糊聚类图像分割[J].电子与信息学报, 2014, 36(11): 2730-2736.

[27]侯格贤,毕笃彦,吴成柯.图像分割质量评价方法研究[J].中国图象图形学报, 2000, 5(1): 39-43.

YAO Longyang was born in 1989. He is an M.S. candidate at Chongqing University of Posts and Telecommunications. His research interests include rough set and granular computing, etc.

姚龙洋（1989-），男，河南洛阳人，重庆邮电大学硕士研究生，主要研究领域为粗糙集，粒计算等。

ZHANG Qinghua was born in 1974. He received the Ph.D. degree from Southwest Jiaotong University in 2010. Now he is a professor at Chongqing University of Posts and Telecommunications. His research interests include rough set and granular computing, etc.

张清华（1974—），男，重庆人，2010年于西南交通大学获得博士学位，现为重庆邮电大学理学院教授，主要研究领域为粗糙集，粒计算等。

HU Shuaipeng was born in 1989. He is an M.S. candidate at Chongqing University of Posts and Telecommunications. His research interests include rough set and granular computing, etc.

胡帅鹏（1989—），男，河南平顶山人，重庆邮电大学硕士研究生，主要研究领域为粗糙集，粒计算等。

ZHANG Qiang was born in 1992. He is an M.S. candidate at Chongqing University of Posts and Telecommunications. His research interests include rough set and granular computing, etc.

张强（1992—），男，甘肃兰州人，重庆邮电大学硕士研究生，主要研究领域为粗糙集，粒计算等。

Rough Entropy for Image Segmentation Based on Approximation Sets and Particle Swarm Optim izationƽ

YAO Longyang1, ZHANG Qinghua1,2+, HU Shuaipeng1, ZHANG Qiang2
1. Chongqing Key Laboratory of Computational Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
2. School of Science, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
+ Corresponding author: E-mail: zhangqh@cqupt.deu.cn

Key words:image segmentation; rough set; approximation set; granular computing; particle swarm

Abstract:Image segmentation method based on the classical rough set theory is lacking of accurate classification on the uncertainty of target image edge boundaries, and classical rough set information system which is built for an image w ith a priori granularity does not reflect the roughness information between different particle size objectives accurately. Based on the theory of approximation set of rough set model, this paper adopts an adaptive optimal graining method on the rough set representation of the image, and then builds the upper and lower approximation sets of the target and background images. According to the approximate set ideas, this paper accurately describes the edge boundaries of the target set, and improves the efficiency of the rough set approximation set maximum rough entropy combined w ith particle swarm algorithm at the same time, finally obtains the optimal segmentation threshold. The experimental results show that this method is feasible and effective.

doi:10.3778/j.issn.1673-9418.1506016 E-mail: fcst@vip.163.com

文献标志码：A

中图分类号：TP391