A Parameterization of the Canonical Bases of Affine Modified Quantized Enveloping Algebras∗

Jie XIAO Minghui ZHAO

1 Introduction

Let U+be the positive part of the quantized enveloping algebra U associated with a Cartan datum.In the case of finite type,Lusztig gave two approaches to construct the canonical basis B of U+(see[11]).The first one is an elementary algebraic construction.By using the Ringel-Hall algebra realization of U+,the isomorphism classes of representations of the corresponding Dynkin quiver form a PBW-type basis of U+and there is an order on this basis.Under this order,the transition matrix between this basis and a monomial basis is a unipotent lower triangular matrix.By a standard linear algebra method one can get a bar-invariant basis,which is the canonical basis B.The second one is a geometric construction.Lusztig constructed the canonical basis B by using perverse sheaves and intersection cohomology.The geometric construction of B was generalized to the cases of all types in[12].In the case of affine type,Lin,Xiao and Zhang in[10]provided a process to construct a PBW-type basis of U+and the canonical basis B by using the Ringel-Hall algebra approach.

Letbe the modified quantized enveloping algebra obtained from U by modifying the Cartan partwherePis the weight lattice.can be considered as the limit of tensor products of the highest weight modules and the lowest weight modules.Lusztig introduced the canonical bases of the tensor products and then the canonical basis[13–14]).Kashiwara also studied the algebraand its canonical basis(see[9]).

Happel studied the bounded derived categoryDb(Λ)of a finite dimensional algebra Λ in[6–7].In the case that Λ is hereditary and representation- finite,he proved that there is a bijection between the isomorphism classes of indecomposable objects inR=Db(Λ)/T2and all the roots of the corresponding Lie algebra,whereTis the translation functor in the triangulated categoryDb(Λ).HenceRis called a root category.It was proved in[15]thatRis still a triangulated category.In[15–16],Peng and Xiao gave a realization of all symmetrizable Kac-Moody Lie algebras via the root categories of finite-dimensional hereditary algebras.

Note that the construction of the canonical basisis abstract and depends on the construction of the canonical basis B of U+.Inspired by the method of Peng and Xiao,we want to study the relations between the canonical basisand the corresponding root categoryR.In this paper, first we associate a settoR.In[10],Lin,Xiao and Zhang associated a setMto a hereditary category and the definition ofis based on that ofM.However,is independent of the embedding of the hereditary category toR.Fixing an embedding of the hereditary category toR,we can get a bijection betweenand the canonical basisfor everyλ∈P.Hence we say that the setprovides a parameterization of the canonical basis.

Since[21],it has been an open problem:How to realize the whole quantized enveloping algebras by using Hall algebras from derived categories or root categories.A lot of efforts have been paid on the progress(see[3,8,20,22])and the most recent progress is given by Bridgeland in[1].We hope that the main result in the present paper can provide a strong evidence for the connection between canonical bases and root categories.

In Section 2,we first give some notations of quantized enveloping algebras and modified quantized enveloping algebras.Then we review the definitions of Ringel-Hall algebras and root categories.In Section 3,we study the case of finite type,which is simpler and can reflect the idea clearly.In Section 4,we study the case of affine type.We first review the construction of the PBW-type basis of U+in[10].Then we define a setdepending on the corresponding root categoryRand a PBW-type basis ofwithas an index.By a standard linear algebra method,we get a bar-invariant basis and prove that each element in it is the leading term of an element inAt last,we prove that there is a bijection between

2 Preliminaries

2.1 Quantized enveloping algebras

Let Q be the field of rational numbers and Z be the ring of integers.LetIbe a finiteindex set withbe a generalized Cartan matrix.Denote byr(A)the rank ofA.LetP∨be a free Abelian group of rank 2n−r(A)with a Z-basisandbe the Q-linear space spanned byWe callthe dual weight lattice and h the Cartan subalgebra.We also define the weight lattice to be

Setand choose a linearly independent subsetsatisfyingor 1 for alli,j∈I,s=1,···,n−rankA.The elements of Π are called simple roots,and the elements of Π∨are called simple coroots.The quintuple(A,Π,Π∨,P,P∨)is called a Cartan datum associated with the generalized Cartan matrixA.

We shall review the definition of quantized enveloping algebras(see[14]).From now on,assume that the generalized Cartan matrixA=(aij)i,j∈Iis symmetric.

Fix an indeterminatev.For anyn∈Z,set

2.2 Modified quantized enveloping algebras

Let us review the definition of the modified form˙U of U(see[13–14]).

For any

Here,the setIis viewed as a subset ofPandiis identified withαifor eachi∈I.The images of summands U(β)underform the weight space decomposition

Note thatunless

There is a natural associative Q(v)-algebra structure oninherited from that of U.It is defined as follows:For anysuch thatand any

2.3 Ringel-Hall algebras

In this subsection,we shall review the definition of Ringel-Hall algebras(see[5,10,18]).

A quiverQ=(I,H,s,t)consists of a vertex setI,an arrow setH,and two mapss,t:H→Isuch that an arrowρ∈Hstarts ats(ρ)and terminates att(ρ).

Letkbe a field and Λ =kQbe the path algebra ofQoverk.Denote by mod-Λ the category of finite dimensional left Λ-modules and rep-Qthe category of finite dimensional representations ofQoverk.It is well-known that mod-Λ is equivalent to rep-Q.We shall identify Λ-modules with representations ofQunder this equivalence.

LetPbe the set of isomorphism classes of finite dimensional nilpotent Λ-modules and ind(P)be the set of isomorphism classes of indecomposable finite dimensional nilpotent Λ-modules.For anyα∈P, fi x a Λ-moduleM(α)in the isomorphism classα.

The set of isomorphism classes of nilpotent simple Λ-modules is indexed by the setIand the Grothendieck groupG(Λ)of mod-Λ is the free Abelian group ZI.For any Λ-moduleM,the dimension vectoris an element inG(Λ)=ZI.

The Euler formis defined by

whereFor any Λ-modulesMandN,one has

The symmetric Euler form is defined byThis gives rise to a symmetric generalized Cartan matrixThe generalized Cartan matrixAdepends only on the underlying graph of quiverQ.

From now on,letkbe a finite field withqelements.Given three modulesL,MandNin mod-Λ,letbe the number of Λ-submodulesWofLsuch thatW⋍NandL/W⋍Min mod-Λ.LetBy definition,the Ringel-Hall algebraHq(Λ)of Λ is the Q(v)-vector space with basis{u[M]|[M]∈P}whose multiplication is given by

It is easily seen thatis an associative Q(v)-algebra with unitu[0],where 0 denotes the zero module.Note that,the Ringel-Hall algebrais an NI-graded algebra by dimension vectors of modules.

The twisted Ringel-Hall algebrais defined as follows.Setvector space and define the multiplication by

LetSibe the nilpotent simple module corresponding toi∈Iand defineThe composition algebrais a subalgebra ofgenerated byuifor alli∈I.For any Λ-moduleM,denote

Note thatbasis of

LetQbe a finite quiver.Then consider the generic Ringel-Hall algebra associated withQ.Letkbe a finite field and Λk=kQ.Denote bythe corresponding twisted Ringel-Hall algebra.LetKbe a set of some finite fieldsksuch that the setis an in finite set.LetRbe an integral domain containing Q andvqk,wherefor anyk∈K.For eachk∈K,the composition algebrais theR-subalgebra ofgenerated by the elementsui(k)for alli∈I.Consider the direct product

and the elementsandwe denote the subalgebra ofgenerated byv,andWe may regard it as anA-algebra generated byui,wherevis viewed as an indeterminate.Finally,definewhich is called the generic composition algebra ofQ.

Then we have the following well-known result of Green and Ringel(see[5,18]).

这个问题，青辰觉得在当前面对的所有问题中，似乎是最不打紧的一个。眼前有着更多关乎云浮命运的大事需要去解决。但师父有此发问，他只得老实作答。

Theorem 2.1Let Q be a connected quiver,A be the corresponding generalized Cartan matrix,andfbe the Lusztig’s algebra of type A.Then there is an isomorphism of algebras:

Hence,we always identifyC∗(Q)with f.

2.4 Root categories

A triangulated category(C,T)is called 2-periodic if the translation functorTsatisfiesT2⋍id.

Letkbe a field.Given a finite dimensional hereditaryk-algebra Λ,denote byDb(Λ)the bounded derived category of the Abelian category mod-Λ andTthe translation functor in this triangulated category.Consider the orbit categoryR(Λ)=Db(Λ)/T2ofDb(Λ)under the equivalent functorT2.LetF:Db(Λ)→R(Λ)be the canonical functor.The translation functorTofDb(Λ)induces an equivalent functor inR(Λ)of order 2,which is still denoted byT.By[15],(R(Λ),T)is also a triangulated category and the functorF:Db(Λ)→R(Λ)sends each triangle inDb(Λ)to a triangle inR(Λ).It is clear that the root categoryR=R(Λ)is a 2-periodic triangulated category.

LetQbe a connected quiver andR(Q)=Db(kQ)/T2.Denote by?Pthe set of isomorphism classes of objects inR(Q)and ind(?P)the set of isomorphism classes of indecomposable objects inR(Q).Note that mod-kQcan be embeded intoR(Q)as a full subcategory and ind(?P)=ind(P)˙∪ind(T(P)),where˙∪means disjoint union.

3 The Finite Type

3.1 The PBW-type basis of U+

In this section,letQbe a connected Dynkin quiver,kbe a finite field and Λ=kQ.Denote by Φ+(resp. Φ−)the set of positive(resp.negative)roots of the Dynkin quiver Q.Note that Φ+and Φ−can be viewed as subsets of ZI.By Gabriel’s theorem,the map dim induces a bijection between ind(P)and Φ+.Given a positive rootα,the corresponding isomorphism class is also denoted byα.

SinceQis representation-directed,we can define a total order on the set

By[19],we have the following proposition.

Proposition 3.1The set

3.2 PBW-type basis of

LetR(Q)be the root category corresponding to a connected Dynkin quiverQover some finite fieldk.Remember thatis the set of isomorphism classes of indecomposable objects inR(Q).LetThen Φ is the root system of the corresponding Lie algebra and there is a bijection betweenand Φ by Gabriel’s theorem.Note thatFor any elementα ∈Φ,we also denote byM(α)the corresponding object inR(Q).

3.3 A bar-invariant basis of

As before,letQbe a connected Dynkin quiver andR(Q)be the corresponding root category.Remember that the set of positive rootsFor any a,b:define b≺a if and only if there exists somesuch thatandFor anyif and only if

For anythere exists a monomialw∗(c)on Chevalley generatorsuisatisfying

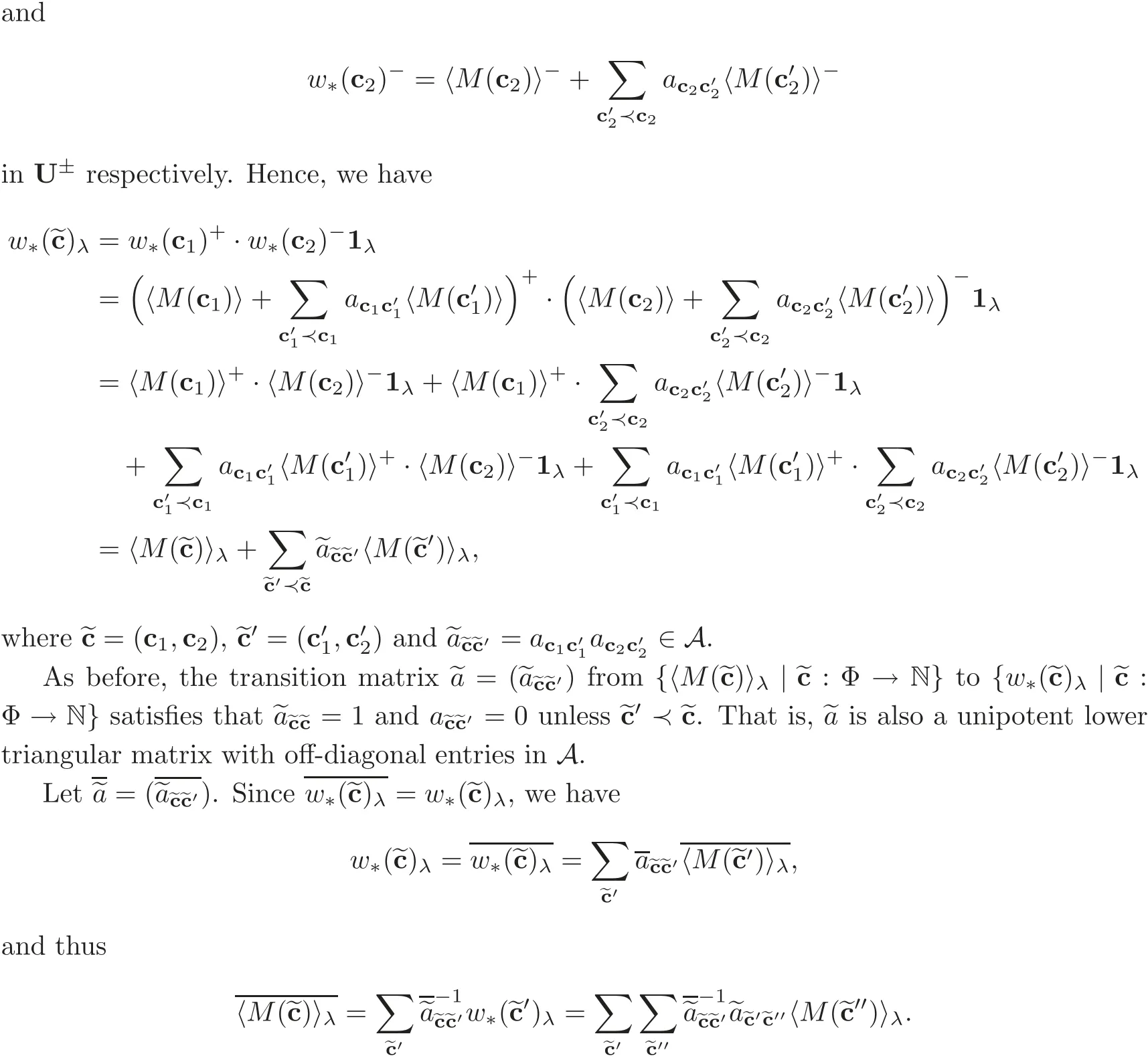
LetThe matrixis again a unipotent lower triangular matrix andThere exists a unique unipotent lower triangular matrixwith off-diagonal entries insuch thatThen we get a bar-invariant basis of

3.4 A parameterization of the canonical basis of

Letbe the modified quantized enveloping algebra corresponding to the quiverQandbe the canonical basis of

Proof The first bijection fromcomes from our construction ofand the second bijection fromcomes from(2.1).By Theorem 3.1,Hence,is a bijection.

4 The Affine Type

4.1 The PBW-type basis of U+

We first review the construction of the PBW-type basis in[2,4,10,23].

4.1.1 The integral basis arising from the Kronecker quiver

LetQbe the Kronecker quiver withI={1,2}andH={ρ1,ρ2}:

Letkbe a finite field withqelements,be the path algebra ofQ.

The set of dimension vectors of indecomposable Λ-modules is

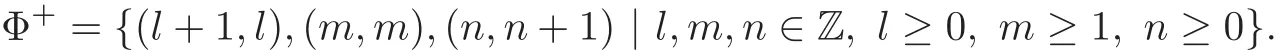
The dimension vectors(l+1,l)and(n,n+1)correspond to preprojective and preinjective indecomposable Λ-modules respectively.

Remember thatPis the set of isomorphism classes of finite dimensional Λ-modules.Denote bythe Ringel-Hall(resp.twisted Ringel-Hall)algebra of Λ.

De fi ne

whereM(n+1,n)(resp.M(n,n+1))is the corresponding Λ-module of the dimension vector(n+1,n)(resp.(n,n+1))for anyn∈N.Letδ=(1,1).For anyn≥1,define

4.1.2 The integral basis arising from a tube

Let Δ = Δ(n)be the cyclic quiver whose vertex set isand whose arrow set is

Letkbe a finite field withqelements,be the category of finite dimensional nilpotent representations of Δ(n)overk.For anyi∈Δ0,denote bySithe corresponding simple object inT.For anyi∈Δ0andl∈N,denote bySi[l]the indecomposable object inTwith topSiand lengthl.Note thatSi[l]is independent of the choice of finite fields.LetPbe the set of isomorphism classes of objects inT.Denote byH(resp.H∗)the corresponding Ringel-Hall algebra(resp.the twisted Ringel-Hall algebra).Since the Hall polynomials always exist in this case,they are regarded as generic forms.Denote byC∗the twisted composition subalgebra ofH∗.

Let Π be the set ofn-tuples of partitionsis a partition of some non-negative integer.For eachπ∈Π,define an object inT

In this way,we obtain a bijection between Π andP.

Ann-tuplepartitions in Π is called aperiodic,if for eachl≥1 there exists somei=i(l)∈Δ0such thatDenote by Πathe set of aperiodicn-tuples of partitions.An objectMinTis called aperiodic ifM⋍M(π)for someπ∈Πa.For any dimension vectordefineand

For any objectsMandNinT,there exists a unique(up to isomorphism)extensionLofMbyNwith the minimal dimEnd(L).The extensionLis called the generic extension ofMbyN,which is denoted by

Let Ω be the set of all words on the alphabet Δ0.For eachset.Then there is a unique p(w)=π∈Π such thatIt has been proved in[17]thatπ=p(w)∈Πaand p induces a surjection p:

Proposition 4.2(see[4,10])be a section of distinguished words.Then bothAnd the transition matrix between these two bases is a unipotent lower triangular matrix with off-diagonal entries in A.

It has been proved in[4]that the basisis independent of the choice of the sections of distinguished words.

4.1.3 The integral bases arising from preprojective and preinjective components

Letkbe a finite field withqelements andLetQbe a connected tame quiver without oriented cycles and Λ=kQbe the corresponding path algebra.Denote by Prep and Prei the sets of isomorphism classes of indecomposable preprojective and preinjective Λ-modules respectively,which are independent of the choice of finite fields.Letthe Ringel-Hall(resp.twisted Ringel-Hall)algebra of Λ.

Since Prei is representation-directed,we can define a total order on the set

4.1.4 The integral basis for the generic composition algebra

Letkalso be a finite field withqelements andLetQbe a connected tame quiver without oriented cycles and Λ=kQbe the corresponding path algebra.

First consider the embedding of the category of representations of the Kronecker quiver into that ofQ.

Letebe an extending vertex ofQandP=P(e)be the projective cover of a simple moduleSe.Letandδbe the minimal imaginary root vector.Note thatand there exists a unique indecomposable preprojective moduleLsuch thatMoreover,HomΛ(L,P)=0 and ExtΛ(L,P)=0.Let C(P,L)be the smallest full subcategory of mod-Λ which containsPandLand is closed under taking extensions,kernels of epimorphisms and cokernels of monomorphisms.The categoryis equivalent to the module category of the Kronecker quiverKoverk.Thus we have an exact embeddingF:mod-kKmod-Λ.Note that the embeddingFis independent of the choice of finite fields.Hence,this gives rise to a monomorphism of algebrasF:we have definedfor anym∈N.De fine

List all non-homogeneous tubesin mod-Λ (in facts≤3).For eachbe the period ofbe the corresponding generic composition algebra andbe its integral form as we did in Section 4.1.2.For eachTi,denote bythe set of aperiodicri-tuples of partitions.We have constructed in Section 4.1.2 the elementsand the

LetMbe the set of

where〉are defined in Section 4.1.3,Eπicis defined in Section 4.1.2 andis defined in Section 4.1.1.

Note that the setis contained inWe have the following proposition.

Proposition 4.4(see[10])

From this basis we can get a bar-invariant basis.But it is not the one considered by Lusztig.Hence in[10],another PBW-type basis is constructed.Let us review its definition.

There is a bilinear form(−,−)ondefined in[5].It is also well-defined onwhich coincides with the one defined by Lusztig in[14].Consider the Q(v)-basis

Letbe thewith the basiswhereis a partition.R(C∗(Q))is a subalgebra of

Letbe the subalgebra ofwith the basisFor anyα,β∈NI,defineα≤βifβ−α∈NI.If.Define

In[10],it is proved that

4.2 The PBW-type basis of

LetQbe a connected tame quiver without oriented cycles andbe the corresponding root category over some finite fieldk.Remember thatis the set of isomorphism classes of objects inR(Q)andis the set of isomorphism classes of indecomposable objects incan be divided into four parts as follows:

Fix an embedding of mod-kQintoand T is the set of isomorphism classes of all indecomposable regular representations ofQ.T consists of isomorphism classes of indecomposable representations in homogeneous tubes and non-homogeneous tubesappearing in mod-kQ.

Note that the categoryR(Q),so the setdepends only on the underlying graph of Q.IfQ′is another quiver such thatthey give the same set

Given any symmetric generalized Cartan matrixA=(aij)n×nof the affine type,consider a quiverQ,the quantum enveloping algebra U and the modified quantized enveloping algebra U˙ corresponding toA.

Remember that mod-kQcan be embedded intoR(Q)as a full subcategory and

Lemma 4.2The transition matrix from under the order＜defined above is an invertible lower triangular matrix,whose diagonal entries are powers of v and off-diagonal entries belong to A.

Proof For anyx,y∈f homogeneous,write

From the definition of the order≺onM,

4.3 A bar-invariant basis of˙U1λ

As before,letQbe a connected tame quiver without oriented cycles andbe the corresponding root category.There is an order≺on the setMin[10].For anydefineif and only ifwhere

For any c∈M,there exists a monomial mcon Chevalley generatorsuisatisfying

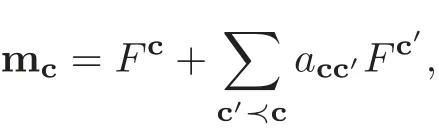
whereacc′∈A(see[10]).Note that the transition matrixsatisfies thatThat is,ais a unipotent lower triangular matrix.

Letwe have

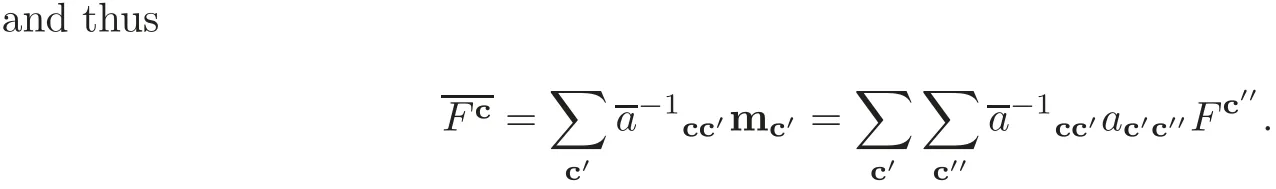
LetThe matrixhis again a unipotent lower triangular matrix andSimilar to the case of finite type,there exists a unique unipotent lower triangular matrixwith off-diagonal entries insuch thatThen the canonical basis of f is

As before,the transition matrixsatisfies thatunlessThat is,is a unipotent lower triangular matrix with off-diagonal entries inA.

Letwe have

LetThe matrixis again a unipotent lower triangular matrix andThere exists a unique unipotent lower triangular matrixwith off-diagonal entries inThen we get a bar-invariant basis of

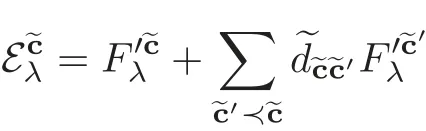
withWe denote this basis by

Theorem 4.1

Proof We use the above notations.

First,by the definition of?a,we have

The proof is finished.

Remark 4.1 Although we use the embedding of mod-kQintoR(Q)to construct the basisthis theorem shows that this basis is independent of the choice of the orientation ofQin fact.

4.4 A parameterization of the canonical basis of˙U1λ

Letbe the modified quantized enveloping algebra corresponding to the quiver

Qandbe the canonical basis of

Theorem 4.2We have a bijection

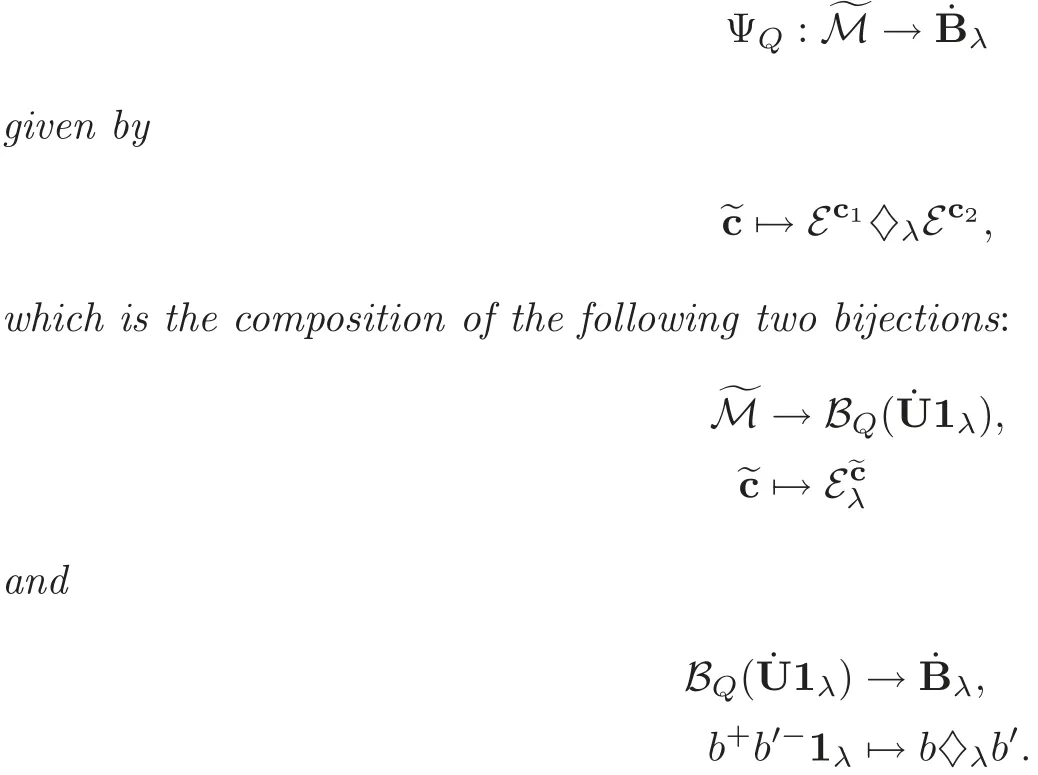
Proof The first bijection fromcomes from our construction ofand the second bijection fromcomes from(2.1).By Theorem 4.1,Hence,is a bijection.

Note that the setdepends only on the root categoryR(Q),instead of on the embedding of mod-kQintoR(Q).Then all elements ingive a parameterization of the canonical basis of the modified quantized enveloping algebra by Theorem 4.2.

[1]Bridgeland,T.,Quantum groups via Hall algebras of complexes,Ann.of Math.,177(2),2013,739–759.

[2]Chen,X.,Root vectors of the composition algebra of the Kronecker algebra,Algebra Discrete Math.,1,2004,37–56.

[3]Cramer,T.,Double Hall algebras and derived equivalences,Adv.Math.,224(3),2010,1097–1120.

[4]Deng,B.,Du,J.and Xiao,J.,Generic extensions and canonical bases for cyclic quivers,Canad.J.Math.,59(5),2007,1260–1283.

[5]Green,J.A.,Hall algebras,hereditary algebras and quantum groups,Invent.Math.,120(2),1995,361–377.

[6]Happel,D.,On the derived category of a finite-dimensional algebra,Comment.Math.Helv.,62(3),1987,339–389.

[7]Happel,D.,Triangulated Categories in the Representation Theory of Finite-Dimensional Algebras,Cambridge University Press,Cambridge,1988.

[8]Kapranov,M.,Heisenberg doubles and derived categories,J.Algebra,202(2),1998,712–744.

[9]Kashiwara,M.,Crystal bases of modified quantized enveloping algebra,Duke Math.J.,73(2),1994,383–413.

[10]Lin,Z.,Xiao,J.and Zhang,G.,Representations of tame quivers and affine canonical bases,Publ.Res.Inst.Math.Sci.,47(4),2011,825–885.

[11]Lusztig,G.,Canonical bases arising from quantized enveloping algebras,J.Amer.Math.Soc.,3(2),1990,447–498.

[12]Lusztig,G.,Quivers,perverse sheaves,and quantized enveloping algebras,J.Amer.Math.Soc.,4(2),1991,365–421.

[13]Lusztig,G.,Canonical bases in tensor products,Proc.Natl.Acad.Sci.USA,89(17),1992,8177–8179.

[14]Lusztig,G.,Introduction to Quantum Groups,Birkh¨auser,Boston,1993.

[15]Peng,L.and Xiao,J.,Root categories and simple Lie algebras,J.Algebra,198(1),1997,19–56.

[16]Peng,L.and Xiao,J.,Triangulated categories and Kac-Moody algebras,Invent.Math.,140(3),2000,563–603.

[17]Reineke,M.,The monoid of families of quiver representations,Proc.Lond.Math.Soc.,84(3),2002,663–685.

[18]Ringel,C.M.,Hall algebras and quantum groups,Invent.Math.,101(3),1990,583–591.

[19]Ringel,C.M.,The Hall algebra approach to quantum groups,Aportaciones Mat.Comun.,15,1995,85–114.

[20]To¨en,B.,Derived Hall algebras,Duke Math.J.,135(3),2006,587–615.

[21]Xiao,J.,Hall algebra in a root category,Preprint 95-070,Univ.of Bielefeld,1995.

[22]Xiao,J.and Xu,F.,Hall algebras associated to triangulated categories,Duke Math.J.,143(2),2008,357–373.

[23]Zhang,P.,PBW-basis for the composition algebra of the Kronecker algebra,J.Reine Angew.Math.,527,2000,97–116.