Analytic Feynman Integrals of Functionals in a Banach Algebra Involving the First Variation∗

Hyun Soo CHUNGVu Kim TUANSeung Jun CHANG

LetC0[0,T]denote a one-parameter Wiener space;that is the space of continuous real-valued functionsxon[0,T]withx(0)=0.LetMdenote the class of all Wiener measurable subsets ofC0[0,T]and letmdenote Wiener measure.(C0[0,T],M,m)is a complete measure space,and we denote the Wiener integral of a Wiener integrable functionalFby

A subsetBofC0[0,T]is said to be scale-invariant measurable provided thatρBisM-measurable for allρ＞0,and a scale-invariant measurable setNis said to be a scale-invariant null set provided thatm(ρN)=0 for allρ＞0.A property that holds except on a scaleinvariant null set is said to hold scale-invariant almost everywhere(for short s-a.e.)(see[16]).Throughout this paper we will assume that each functionalF:C0[0,T]→C that we consider is scale-invariant measurable and that

for eachρ＞0.

In 1948,Feynman assumed the existence of an integral over a space of paths,and he used his integral in a formal way in his approach to quantum mechanics(see[15]).Many mathematicians have attempted to give rigorously meaningful definitions of the Feynman integral with appropriate existence theorems and have expressed solutions of the Schrödinger equation in terms of their integrals.One of these approaches was based on the similarity between the Wiener and the Feynman integrals,and procedures were set up by many mathematicians to obtain Feynman integrals from Wiener integrals by analytic extension from the real axis to the imaginary axis.For the procedure of analytic continuation to define the analytic Feynman integral,see[15].Since the analytic Feynman integral was introduced,many mathematicians studied the analytic Feynman integral of functionals in several classes of functionals(see[1–5,7,13]).Also,they obtained various analytic Feynman integration formulas involving the first variation.In particular,in[2],the authors introduced a Banach algebraSwhich contains many functionals used in quantum mechanics,and then established analytic Feynman integrals of functionals inSinvolving the first variation.

In this paper we first recall the Banach algebraSαwhich was introduced in[11]and modified in[9,14].We then obtain the existence of the analytic Feynman integral and the first variation of a functionalFinSα.Also,we obtain analytic Feynman integration formulas involving the first variation.The results in[2]are special case of this paper whenα=i.The formulas and results in this paper are more complicated and more generalized than the results and formulas in[2].In fact,whenα=i,all conditions hold,so they could be omitted naturally.

1 Definitions and Preliminaries

In this section,we recall some definitions and properties from[1–5,7,13].

Definition 1.1LetCdenote the complex numbers,Let F:be a measurable functional such that for each λ＞0,the Wiener integral

Forv〉denote the Paley-Wiener-Zygmund(for short PWZ)stochastic integral.Then we have the following assertions:

(1)For eachexists for a.e.

(2)Ifis a function of bounded variation on〉equals the Riemann-Stieltjes integralfor s-a.e.

(3)The PWZ stochastic integral〈v,x〉has the expected linearity property.

(4)The PWZ stochastic integral〈v,x〉is a Gaussian process with mean 0 and variance

For a more detailed study of the PWZ stochastic integral,see[5–6,8–12].

The following is a well-known integration formula which is used several times in this paper.

Now we recall a modified Banach algebraSαof functionals which was introduced in[11]and used in[9,14].

For each complex numberαwith Re(α2)≤0,letSαbe the class of functionals of the form

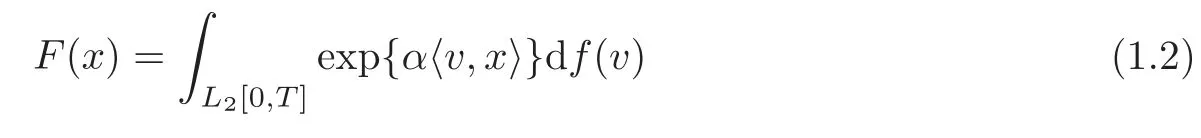
for s-a.e.x∈C0[0,T],wherefis inM(L2[0,T]),the class of all complex valued countably additive Borel measures onL2[0,T].

Remark 1.1 Using the techniques similar to those used in[2],we can show that for eachα ∈C with Re(α2)≤0,the classSαis a Banach algebra with the norm

One can show that the correspondencef→Fis injective,and carries convolution into pointwise multiplication and that for each complex numberαwith Re(α2)≤0,the spaceSαis a Banach algebra.In particular,ifα=i,thenSiis the Banach algebraSintroduced by Cameron and Storvick in[2].For more details,see[9,11,14].

2 Analytic Feynman Integrals of Functionals in Sα

In this section,we establish the analytic Feynman integral of functionals inSα.

Remark 2.1(1)Letγ1=a+ibandγ2=c+idbe nonzero complex numbers witha≤0 andc≥0.First,we note that

In view of(1),the region Γαhas sufficiently many complex numbersλ.

(3)Now we describe the region Γαfor eachα.Letα2=a+ibandλ=c+idbe complex numbers witha≤0 andc＞0.Then for eachα,we can describe the region Γαas follows:

(i)Whend=0 orb=0,Γα=C+.

(ii)Whend/=0 andb/=0,for a givenα,ifb＞0,then the region Γαis given byand ifb＜0,then the region Γαis given by

(iii)The region Γαalways contains all positive real numbers.

In particular,whenαis pure imaginary,Γα=C+.

In our first lemma,we establish the existence of the analytic Wiener integral of a functionalFinSα.

Lemma 2.1Let F∈Sαbe given by(1.2).Then the analytic Wiener integral

whereis given by(2.1).Moreover,the functionis well-defined on the region Γα.In fact,for allλ∈Γα.Also,for allλ＞0.At last,we will show thatJ∗(λ)is analytic on Γα.To do this,let Λ be any simple closed contour in Γα.Then using the Fubini theorem and the Cauchy theorem,we have

To do this,we recall the region Γαas in Remark 2.1.Note that for a given nonzero real numberqwhich satisfies the condition(2.3),there exists a sequenceinso thatasn→∞.In fact,if we lettheninandasn→∞.By Remark 2.1 and Lemma 2.1,for alll=1,2,···.Hence using the dominated convergence theorem,for every nonzero real numberqwhich satisfies the condition(2.3)above,

3 The First Variation and Analytic Feynman Integrals

In this section we establish the existence of first variation ofFinSαand establish various analytic Feynman integrals involving first variations ofF.

We start this section by giving the definition of the first variation of a functionalFonC0[0,T].

Definition 3.1Let F be a functional defined on C0[0,T].Then the first variation of F is defined by the formula

exists for s-a.e.x∈C0[0,T].However,the integral(3.3)might not exist because the product ofL1-functionals might not be inL1.Hence we should give a condition forfas follows:If Re(α2)≤0 and Equation(3.2)holds,then the integral(3.3)always exists.

In our next theorem,we obtain the formula for the first variation of functionals fromSαintoSα.

Proof From Theorem 3.1,the first variationδF(x|u)as a function ofxis an element ofSα.Hence using Equation(2.5),we have

for every nonzero real numbersqas in Theorem 3.2.

The following lemma was established in[1].

Equation(3.11)is called the Cameron-Storvick formula on C0[0,T].

In the last main result,we obtain the Cameron-Storvick formula for analytic Feynman integral of functionalsFandGinSα.

Theorem 3.3Let F and G be elements of Sαwhose associated measures f and g satisfy the condition(3.9)and let q be as in Theorem3.2.Then

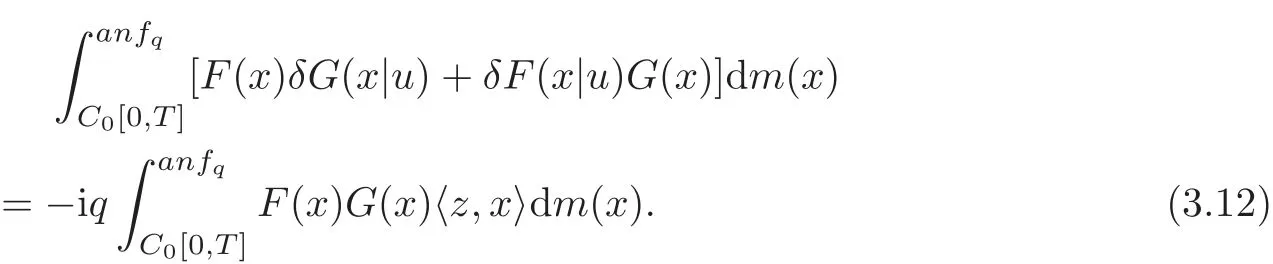
Proof ForFandGinSα,letL(x)=F(x)G(x).Then using Equation(3.11)withFbeing replaced byL,we obtain Equation(3.12).In fact,the left-hand side of Equation(3.12)always exists because the associated measuresfandgsatisfy the condition(3.9).

The following corollaries immediately follow from Theorem 3.3.

Proof We easily obtain Equation(3.14)by replacingGwithFnin Equation(3.12)above and using the mathematical induction forn.

Remark 3.2(1)As mentioned in Section 2,ifα=i,thenSαis the Banach algebraSintroduced in[2].Furthermore,all conditions in the previous sections and this section hold,so all results and formulas in[2]are corollaries of our results and formulas in this paper.

(2)In[2],the authors obtained the existence of the analytic Wiener integral ofFinSon C+.We obtained the existence of the analytic Wiener integral ofFinSαon Γαwhich is a subset of C+becauseαmay not be a pure imaginary number.In fact,ifαis a pure imaginary number,then we can obtain the existence of the analytic Wiener integral ofFinSαon C+.

AcknowledgmentThe authors thank the referees for their helpful suggestions which led to the present version of this paper.

[1]Cameron,R.H.and Storvick,D.A.,Feynman integral of variation of functionals,Gaussian Random Fields,World Scientific,Singapore,1980,144–157.

[2]Cameron,R.H.and Storvick,D.A.,Some Banach algebras of analytic Feynman integrable functionals,Analytic Functions,Kozubnik,1979,Lecture Notes in Math.,798,Springer-Verlag,Berlin,1980,18–67.

[3]Cameron,R.H.and Storvick,D.A.,Analytic Feynman integral solutions of an integral equation related to the Schrödinger equation,J.Anal.Math.,38,1980,34–66.

[4]Cameron,R.H.and Storvick,D.A.,Relationships between the Wiener integral and the analytic Feynman integral,Rend.Circ.Mat.Palermo(2)Suppl.,17,1987,117–133.

[5]Chang,S.J.,Choi,J.G.and Chung,H.S.,The approach to solution of the Schrödinger equation using Fourier-type functionals,J.Korean Math.Soc.,50,2013,259–274.

[6]Chang,S.J.,Chung,H.S.and Skoug,D.,Convolution products,integral transforms and inverse integral transforms of functionals inL2(C0[0,T]),Integral Transforms Spec.Funct.,21,2010,143–151.

[7]Chang,K.S.,Johnson,G.W.and Skoug,D.L.,The Feynman integral of quadratic potentials depending on two time variables,Pacific J.Math.,122,1986,11–33.

[8]Chung,H.S.and Chang,S.J.,Some applications of the spectral theory for the integral transform involving the spectral representation,J.Funct.Space Appl.,2012,DOI:10.1155/2012/573602.

[9]Chung,H.S.,Choi,J.G.and Chang,S.J.,Conditional integral transforms with related topics,Filomat,26,2012,1147–1158.

[10]Chung,H.S.,Skoug,D.and Chang,S.J.,A Fubini theorem for integral transforms and convolution products,Int.J.Math.,2013,DOI:10.1142/S0129167X13500249.

[11]Chung,H.S.and Tuan,V.K.,Generalized integral transforms and convolution products on function space,Integral Transforms Spec.Funct.,22,2011,573–586.

[12]Chung,H.S.and Tuan,V.K.,Fourier-type functionals on Wiener space,Bull.Korean Math.Soc.,49,2012,609–619.

[13]Chung,H.S.and Tuan,V.K.,A sequential analytic Feynman integral of functionals inL2(C0[0,T]),Integral Transforms Spec.Funct.,23,2012,495–502.

[14]Chung,H.S.and Tuan,V.K.,Currigendum:Generalized integral transforms and convolution products on function space,Integral Transforms and Special Functions,24,2013,509–509.

[15]Feynman,R.P.,Space-time approach to non-relativistic quantum mechanics,Rev.Modern Phys.,20,1948,115–142.

[16]Johnson,G.W.and Skoug,D.L.,Scale-invariant measurability in Wiener space,Pacific J.Math.,83,1979,157–176.